引汉济渭工程调水区月径流预报模型研究

2021-11-13杨元园黄生志刘登峰孟二浩

西安理工大学学报 2021年3期

李静，黄强，杨元园,2，黄生志，刘登峰，孟二浩

(1.西安理工大学西北旱区生态水利国家重点实验室，陕西西安 710048；2.陕西省水资源与环境重点实验室，陕西西安 710048)

径流具有高度复杂性、非平稳性、动态性和非线性的特点，它的现象和特征模式不容易被预报。近年来许多学者对高精度径流预报进行了研究[1-2]。传统的时间序列预测模型是在考虑一致性条件下进行的，而机器学习能更好地捕捉径流非平稳性和非一致性的特点。随着高精度预报模型及组合预报模型不断被提出[3-6]，评价模型或组合模型的预报结果非常重要。

目前，大多数研究学者对预报结果的评判往往选用单一评价指标。不同评价指标对模型结果分析存在差异，若仍用单一指标来评价预报精度，很有可能造成模型预报结果与实际相差较大而整体性精度较高。因此，构建综合评价指标系统对预报结果进行评价至关重要。

均方根误差(root mean squared error，RMSE)可用来评价预测值与真实值之间的偏差，被广泛用于模型计算结果评价[7-8]。平均绝对百分误差(mean absolute percentage error，MAPE)是一个常用于衡量预测准确性的统计指标，如时间序列的预测[9-10]。NASH效率系数(nash-sutcliffe efficiency coefficient，NSE)常用来评价模型质量[11-12]。因此，构建由以上三种评价指标组成的综合评价系统，可全面的评价一个模型预报结果的好坏。

自回归滑动平均模型(auto regressive moving average models，ARMA)、人工神经网络模型(artificial neural network models，ANN)、支持向量机(support vector machine models，SVM)常用于中长期径流预报[13-16]。研究高精度的径流预测模型可以有效指导水资源跨流域调度，提高“引汉济渭”工程的水资源利用率，关中地区的缺水情况可以得到有效的解决，促进可持续发展。

预报方法在不断完善，但当前研究主要基于各水文年长序列数据，将长序列拆分为短序列后再进行预报的研究不多。针对径流的特点，径流序列在非汛期比汛期时间长，突变少，两者径流特征相差较大，可将长序列数据系列进行汛期非汛期划分，在划分后的数据基础上，再采用模型进行径流预报。

本文以“引汉济渭”工程调水区黄金峡断面和三河口断面的为研究对象进行月径流预报研究，将径流数据进行汛期和非汛期划分，在此基础上分别构建了基于Huber权重计算的ARMA模型、基于切S型函数进行传递计算的ANN模型和基于径向基函数为核函数和遗传算法进行参数优选的SVM模型，并采用构建的综合评价指标系统对预报结果进行评价，综合选出预报效果最好的模型。可为“引汉济渭”工程提供较为精准的预报模型，为水库优化调度和合理配置水资源提供选择。

1 数据与方法

1.1 数据来源

本次研究选取了黄金峡断面和三河口断面的综合流入径流资料。研究分析了两个断面从1955—2009年共55年的月径流资料。按照8∶2的比例分为率定期及验证期。

1.2 汛期与非汛期划分

对于汛期与非汛期的划分国内外的研究中已存在很多种方法，例如模糊统计法、相对频率法、变点分析法以及片段法等[17]。片段法是将径流序列看作整体算出多年平均值，将突变的数据进行了整体均分，能更准确地确定整体序列的汛期非汛期，作为预报的数据输入。因此本文选用了片段法对月径流量进行分析并进行划分。

片段法是通过对已知的一个N年年径流量序列的样本进行分解，求出多年平均年径流量以及多年平均月径流量。用历史样本中N年序列的对应的多年月平均径流量除以多年年平均径流量，得到的结果为该系列每年12个标准化的月径流不规则因子。

将不规则因子值进行统计分析，因子大于1的月份为汛期，因子小于1的月份为非汛期。计算公式如下：

(1)

分析计算黄金峡断面和三河口断面的55年每月径流量及每年径流量数据序列，得到多年月平均流量和多年年平均流量。

表1为两断面多年月平均径流量和多年年平均径流量。从表1可以看出黄金峡断面流量远比三河口断面流量大，黄金峡和三河口断面多年月平均流量最大的均为7月、8月、9月和10月。

从表1中可以得两断面多年月平均和多年年平均径流量，带入式(1)中进行计算，得到两个断面在55年时间长度内的月径流年内不规则因子，图1为黄金峡和三河口断面年内不规则因子图。

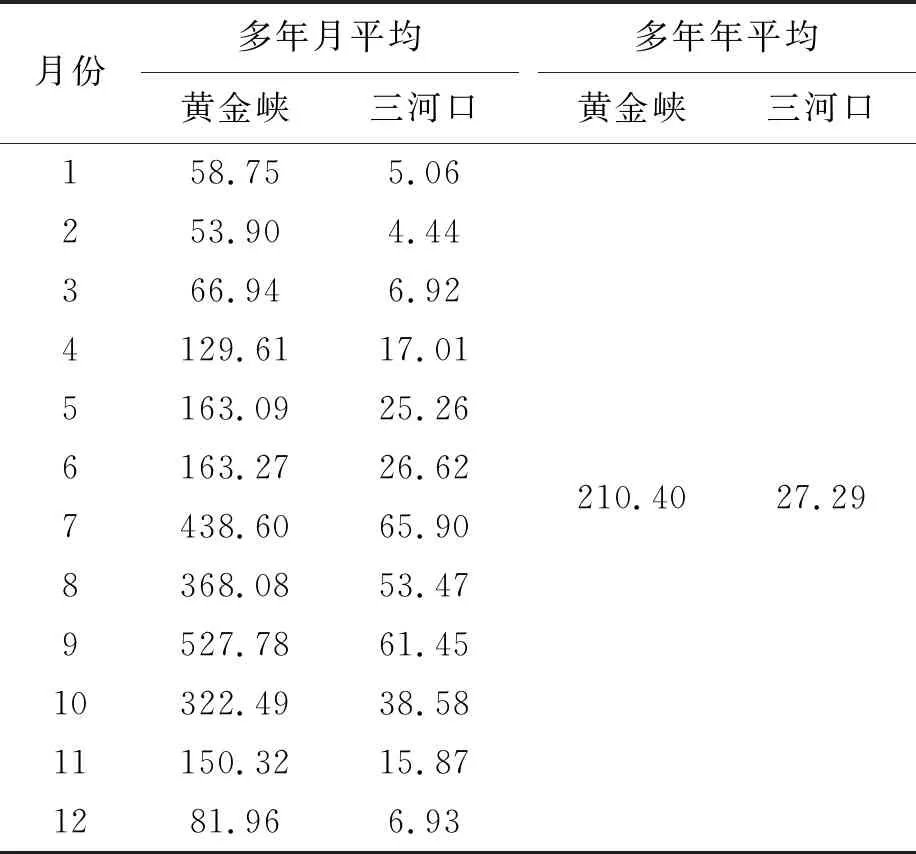
表1 黄金峡和三河口断面径流量Tab.1 Runoff of Huangjinxia and Sanhekou Sections 单位：亿m3

根据汛期非汛期判断准则，从图1可以看出，黄金峡和三河口断面不规则因子超过1的月份共有4个月，为图中橙色部分，因此，两断面的汛期划分为7～10月；非汛期划分为1～6月、11月和12月。

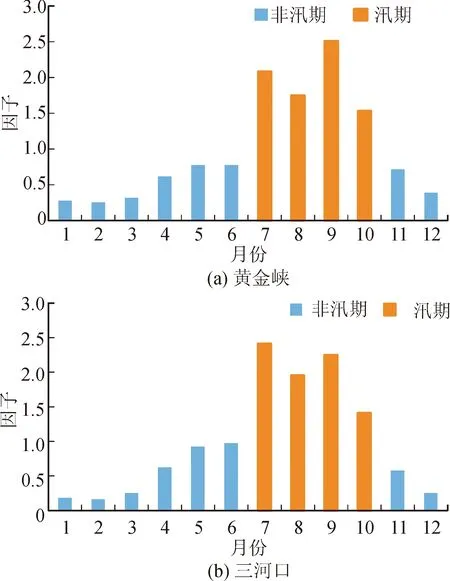
图1 黄金峡和三河口断面年内不规则因子图Fig.1 Annual irregularity factor map of Huangjinxia and Sanhekou sections

1.3 径流预报模型

1)自回归滑动平均模型(ARMA)

ARMA表达式由AR模型的p阶自回归表达式和MA模型的q阶滑动平均表达式共同组成，用权函数中的Huber权重进行一系列计算。

2)人工神经网络模型(ANN)

在径流预报方面，ANN模型主要有输入层、隐藏层和输出层三个部分。传递函数提供了非线性映射潜力，本文选用的是切S型传递函数，该函数能够捕捉水流的非线性关系。训练选取了反向传播监督学习算法。前向传播和后向传播为网络训练的两个阶段，在前向传播阶段，神经元的计算是通过权重实现的。

3)支持向量机模型(SVM)

SVM通过监督学习方式对数据进行二元分类，其决策边界是对学习样本求解的最大边距超平面。验证构造后的核函数对输入空间内的任意Gram矩阵是半正定矩阵是困难的，因此通常的选择是使用现成的核函数。本次研究选取的核函数是径向基函数。在此核函数下，正则化常数C和核函数自带参数γ及误差容限ε对预报效果有较大影响。通过调节参数和结果分析得到本次建立模型的误差容限ε为0.002。在构建模型时，采用遗传算法对正则化常数和核函数自带参数进行优选[18]。

1.4 预报结果评价指标

本文选择了均方根误差(RMSE)、平均绝对百分误差(MAPE)和Nash效率系数(NSE)三个评价指标。用该三个评价指标构建的评价体系，综合评价此次预报构建ARMA、ANN和SVM的预报效果，并进行比较。

RMSE是每个预报值与真实值差值的平方和与观测次数n的比值的平方根，可评价径流序列中高值的预报效果。RMSE值越小，表明该预报径流序列与实测径流序列在高值处的预报效果更好。计算公式如下：

(2)

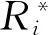
MAPE是绝对百分比误差的平均值，可评价径流序列中平稳值的预报效果。MAPE越小，该径流序列与实测径流序列在平稳期的预报效果更好。计算公式如下：

(3)

式中字母含义同式(2)。

NSE可作为模型的预报效率评价指标。NSE取值范围为(-∞，1)，NSE接近1，表示模型质量好，模型可信度高；NSE接近0，表示预报结果接近观测值的平均值水平，即总体结果可信，但过程模拟误差较大；NSE远远小于0，表示该模型不可靠[19]。计算公式如下：

(4)

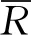
三个评价指标分别从预报结果峰值、预报结果平稳值及模型整体预报效果三个方面对预报结果进行评价，综合评价系统可避免因整体趋势一致而导致的预报精度较高而结果却不理想问题。

1.5 输入变量

由1.1节研究结果可知，黄金峡和三河口断面汛期有4个月、非汛期有8个月。因此，设定7种情形作为本次模型的输入变量，表2为输入变量的情景。

表2 输入变量情景集Tab.2 Input variable scenario set

ARMA、ANN和SVM模型是以数据为驱动的预报模型，选择合适的滞时输入变量个数非常重要，包含不相关的输入将导致较差的模型精确度和复杂度，因此需要分析前期流量对当前流量的影响来确定作为输入变量的取值[20]。在此采用自相关系数法来分析。黄金峡月径流序列和三河口月径流序列的自相关系数计算结果如下(计算公式见文献[21]中式(3-7))。

计算黄金峡径流滞时相关性系数可知，汛期内，1月和4月的径流相关性系数最好，分别为0.28和0.32；非汛期内，径流滞时1月和7月的相关性系数最好，分别为0.31和0.35。因此汛期变量输入选择为情景1和情景4，非汛期为情景1和情景7。

用相同方法得到，三河口汛期径流滞时为1月和4月的相关性系数最好，分别为0.37和0.34；非汛期径流滞时1月、7月的相关性系数最好，分别为0.38和0.41。因此，汛期输入变量的选择为情景1和情景4，非汛期为情景1和情景7。

根据选定的输入情景，分别采用构建的ARMA模型、ANN模型和SVM模型对黄金峡和三河口两个断面进行汛期非汛期月径流预报。

根据构建的综合评价指标分析体系，分别对三种模型的预报结果进行均方根误差、平均绝对百分误差和Nash效率系数计算。分析预报结果，综合评选出三个模型中预报效果最优、预报精度最高的预报模型。

2 结果与讨论

2.1 汛期月径流预报结果

将黄金峡断面和三河口断面汛期数据滞时为1和4月的情景1和情景4的径流数据序列分别带入三种预报模型，得到汛期预报结果。分别计算两断面汛期月径流预报结果与实测数据间的RMSE、MAPE和NSE。图2为黄金峡汛期月径流预报结果。

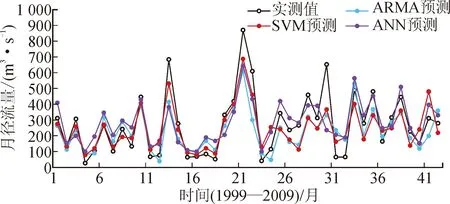
图2 黄金峡汛期月径流预报结果Fig.2 Flood season monthly runoff forecast results of Huangjinxia Section

从图2可以看出，黄金峡汛期月径流三种模型的预报结果较实测数据都有所偏差，径流实测值变化较大，无规律可循。ANN模型结果偏差较大，在峰值处预报值低于实测值，大部分预报值都较实测值偏高，特别是在26～31，趋势发生改变，原因在于在构建ANN模型时，选择的切S型函数，该函数虽然可捕捉非线性关系，但是不能很好地捕捉径流的整体趋势。而ARMA模型的预报结果与ANN相反，整体预报结果较实测值偏低，ARMA模型是传统预报模型，不能很好捕捉径流间的非线性关系，导致预报效果不优。相对于ARMA模型，SVM模型预报结果变化趋势与实测数据更为相似，构建SVM模型时，采用的遗传算法进行参数优选，可有效提高模型的预报能力。三种模型在峰值处的预报结果都偏低。可能原因是在捕捉黄金峡率定期的汛期关系时出现偏差。

表3为黄金峡汛期月径流预报结果分析计算结果。

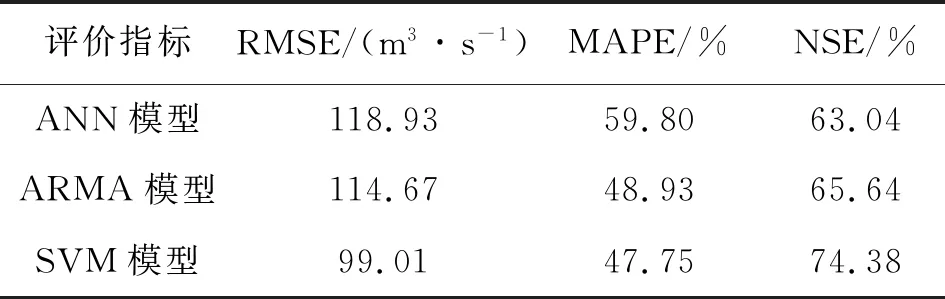
表3 黄金峡汛期月径流预报结果分析Tab.3 Analysis of monthly runoff forecast results in flood season of Huangjinxia Section

从表3可以得到，单从MAPE看，ARMA模型和SVM模型预报效果相差不大，仅相差1.18%，无法准确地确定哪种模型预报效果较好，但是结合RMSE和NSE，可发现SVM模型预报效果明显优于ARMA模型。综合评价指标表明，三种模型预报精度：SVM>ARMA>ANN。

图3为三河口汛期月径流预报结果。

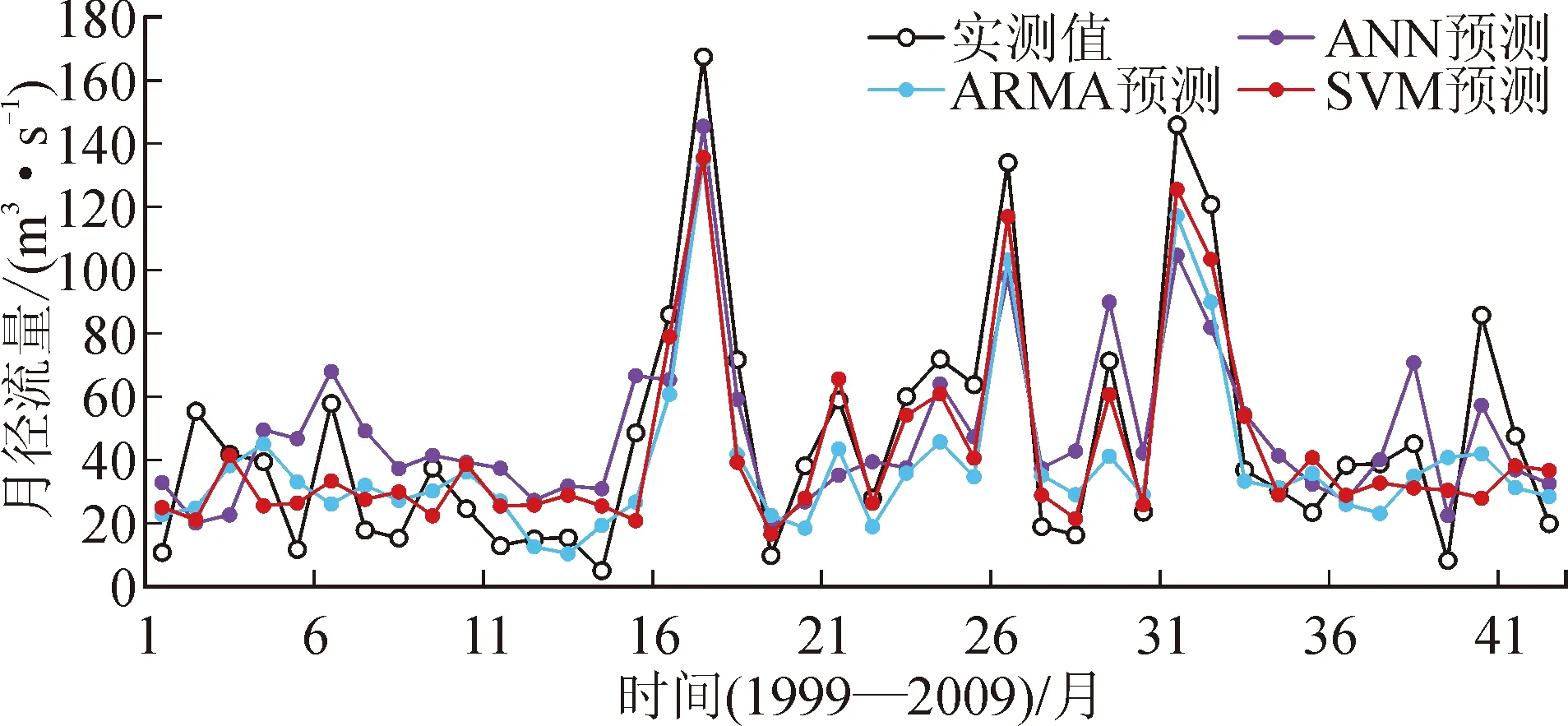
图3 三河口汛期月径流预报结果Fig.3 Flood season monthly runoff forecast results of Sanhekou Section

从图3可以看出，SVM模型预报结果与实测值趋势相似，更接近实测值。表4为三河口汛期月径流预报结果分析计算结果。

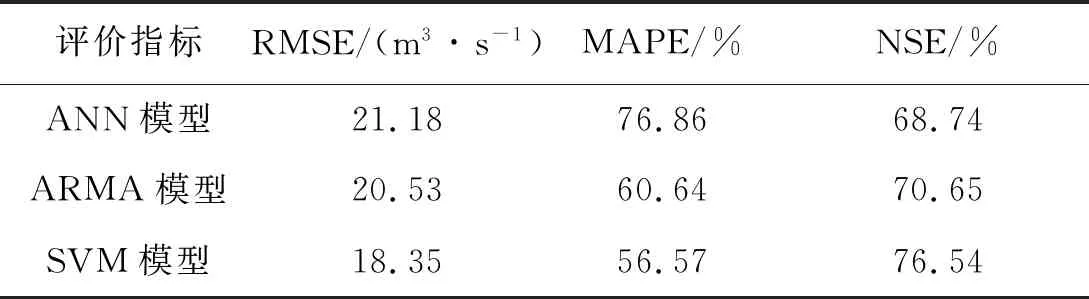
表4 三河口汛期月径流预报结果分析Tab.4 Analysis of monthly runoff forecast results in flood season of Sanhekou Section

从表4可以看出，综合评价指标表明三种模型预报精度：SVM>ARMA>ANN。

2.2 非汛期月径流预报结果

将黄金峡断面和三河口断面的非汛期径流序列滞时为1和7月的情景1和情景7序列分别带入三种预报模型，得到汛期预报结果。分别计算两断面非汛期月径流预报结果与实测数据间的RMSE、MAPE和NSE。图4为黄金峡非汛期三种月径流模型预报结果。

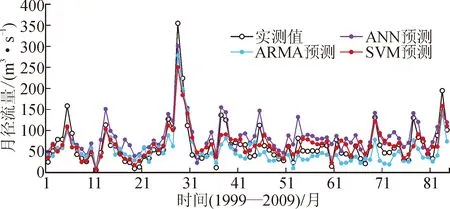
图4 黄金峡非汛期月径流预报结果Fig.4 Non-flood season monthly runoff forecast results of Huangjinxia Section

从图4可以看出，黄金峡非汛期三种模型月径流预报结果SVM模型预报效果最好，ANN预报结果较实测值有较大误差，其中几个月高于实测值，ARMA预报结果连续几个月较实测值过低。但三种模型预报结果整体与实测值趋势变化一致。与汛期相比，非汛期预报结果的整体趋势与实测值并无太大差异，且整体预报结果优于汛期预报结果，三种模型更好地捕捉了非汛期径流间的非线性关系，非汛期径流变化较平稳，规律可循。

表5为黄金峡汛期月径流预报结果分析计算结果。

表5 黄金峡非汛期月径流预报结果分析Tab.5 Analysis of monthly runoff forecast results in non-flood season of Huangjinxia Section

从表5可以看出，三种模型预报精度：SVM>ARMA>ANN。

图5为三河口非汛期月径流预报结果。

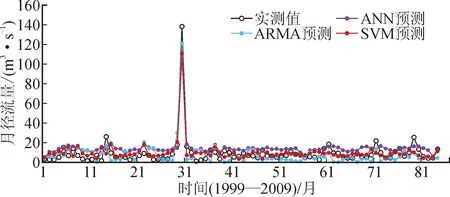
图5 三河口非汛期月径流预报结果Fig.5 Non-flood season monthly runoff forecast results of Sanhekou Section

从图5可以看出，三河口非汛期三种模型预报结果较实测值来说最为接近的是SVM模型，不会过高，也不会过低。预报效果较好。表6为三河口汛期月径流预报结果分析计算结果。

表6 三河口非汛期月径流预报结果分析Tab.6 Analysis of monthly runoff forecast results in non-flood season of Sanhekou section

从表6可以得到，三种模型预报精度：SVM>ARMA>ANN。

2.3 讨论

对于黄金峡和三河口断面的汛期和非汛期月径流预报，ARMA、ANN和SVM中预报效果最好的是SVM模型。该结果与张俊[22]计算结果一致。选取的三个评价指标组成了一个综合的评价体系，更全面地评价三种模型预报效果的准确性。

对于模型的结果分析，ANN模型的泛化能力比较差，有时会陷入局部最优解的困局，而且没有明确的物理机制，导致它在实际应用中会存在一定局限性和不合适性。因此本次构建ANN模型时选择切S型传递函数，该函数能捕捉水流的非线性关系，且选择权重法确定输入神经元的个数。结果表明ANN模型虽然在三个模型中模拟效果不及ARMA和SVM模型，但是结果仍然可信，且ANN模型洪峰预报结果与实测数据较为相近，洪峰预报效果较好。

ARMA模型是传统的预报模型，本文通过构建基于稳健估计的ARMA模型进行径流预报，在构建模型时，选用了Huber权重进行计算。结果表明预报效果较好，存在的问题是ARMA模型在平稳序列的预报结果整体偏低，在非平稳序列的预报结果整体偏高，虽然综合预报效果比ANN好，但是与实际的序列过程还是有所偏差。

SVM模型的预报结果最好，研究结果表明参数的选择对于预报的泛化性能影响较大。本文在构建SVM模型时，选用了径向基函数作为SVM的核函数，将数据运用到高级空间，再通过遗传算法进行参数选择。本次构建的SVM模型在三种预报效果最好，具有较好的泛化能力，能寻找全局最优解且进行快速准确拟合和预报，且从图中可知模型的整体预报趋势与偏差与实测数据都较小。对于非线性和非平稳径流序列，显示出了SVM的优越性。

对于相同断面的汛期和非汛期月径流预报，SVM模型、ARMA模型、ANN模型在非汛期的预报精度高于汛期的预报精度。可能原因是本次径流数据序列在非汛期的变化较为平缓，没有发生突变的情况，模型能更好地捕捉到非汛期径流序列的变化规律。在进行径流预报时，可将径流进行汛期和非汛期划分之后在进行预报。

构建的综合评价指标可从洪峰、平稳期以及整体趋势三个方面评价模型预报结果精度，可帮助选定最合适最有效的预报模型，本次构建的综合评价指标系统对SVM模型、ARMA模型、ANN模型预报结果评价，得到预报效果最好的是SVM模型。

3 结论和展望

3.1 结论

1)综合评价指标系统可以更全面地评价一个模型的预报精度和整体预报结果的好坏。以黄金峡汛期预报结果评价为例，在RMSE作为评价指标时，ANN模型为118.93 m3/s，ARMA模型为114.67 m3/s，SVM模型为99.01m3/s。RMSE可评价径流序列中高值的预测效果，但是ANN模型与ARMA模型的RMSE相差不大。SVM模型的预测效果在高值处最好，ARMA模型略好于ANN模型。在MAPE作为评价指标时，ANN模型的MAPE为59.80%，ARMA模型的MAPE为48.93%，SVM模型的MAPE为47.75%。MAPE可评价径流序列中平稳值的预测效果，SVM模型与ARMA模型的MAPE几乎没有大的差别，ANN模型的预测效果较差一点。在NSE作为评价指标时，ANN模型的NSE为63.04%，ARMA模型的NSE为65.64%，SVM模型的NSE为74.38%。NSE可评价模型的好坏。因此，综合三个评价指标表明：SVM>ARMA>ANN。

2)本文提出的三个评价指标结果综合表明黄金峡和三河口两个断面汛期和非汛期内构建的三个模型SVM的预报效果均最好，ARMA次之，ANN较差，基于结构风险最小化诱导原理SVM模型的预报效果较好。且非汛期预报精度高于汛期预报精度，模型在非汛期更好地捕捉径流变化规律。