智能汽车自动紧急避撞系统的模型建立及分析

纪文煜

(无锡南洋职业技术学院 汽车工程与管理学院，江苏 无锡 214081)

现阶段，汽车安全技术研究方向已经由被动安全防御转向主动安全避撞.汽车传统安全防御系统主要包括ABS(制动防抱死系统)和ESC(车身电子稳定控制系统)，相关系统的可靠应用条件是预设驾驶员操作正确，但是研究表明，超过90%的交通安全事件来源于驾驶员的错误操作，基于此，本文提出了自动紧急避撞系统.文章基于该系统模型深入探讨相关避撞理论，为确保驾驶安全、促进智能汽车安全技术进一步发展奠定了基础.

1 研究背景

AEB(自动制动系统)作为汽车对障碍物进行主动避撞的方式，其与ABS(制动防抱死系统)和FCW(前方碰撞预警系统)存在密切联系.该系统强调以主动制动为依托，可将汽车追尾或是其他碰撞事故出现的几率降至最低.现阶段，在市场上流通的AEB(自动制动系统)产品种类及数量较多，有关部门也制定了一系列用来规范相关产品性能的标准.在周围有突然出现障碍物的特殊工况下，仅凭借自动制动系统无法保证车辆碰撞事故不会发生，此时，便需要进行自动转向.由此可见，要想使避撞问题得到有效解决，自动转向同样发挥着无法被替代的作用[1].

与紧急制动相比，自动转向系统研究的难度更大，最应当引起重视的部分为避撞距离模型.就汽车行驶所遇到紧急情况而言，要想尽快解除警报，关键是要掌握避撞系统介入时间，系统介入过早极易给正常驾驶带来影响，而系统介入过晚将出现避撞失败的问题.由此可见，适宜且准确的避撞时机的确定，可使避撞系统的作用获得最大程度发挥.在进行相关研究时，首当其冲需要确定的便是安全距离相关模型.

智能汽车避撞方式主要有制动、转向、制动+转向.针对上述避撞方式所开展的研究，现已取得一定的成果，主要包括：其一，盘朝奉等人基于自动制动规避，对处于不同工况的运动前车进行分析和验证；其二，Shiller等人以自行车模型为参考，根据转向规避实验所得结果，对纵向距离最小值加以明确，约束条件是“障碍物和本车边界重合”；其三，Seewald等人则认为，要想使仿真实验结果最大程度符合实际情况，约束条件应为侧向位移，即障碍物后边界和本车质心的横向距离满足安全要求[2].

通过上述的分析能够看出，虽然多数研究均对安全距离模型进行了应用，但并没有做到协调统一，也就是说，国内外学者基于紧急避撞系统所开展研究引入的模型均有较为显著的差异性存在，但未能做到客观且全面的分析，这也使得研究所得结论无法为日后设计及开发避撞系统的工作提供全过程指导.本文在此背景基础上，先对车辆外形与尺寸加以考虑，而后建立紧急避撞系统模型，再以运动学视角为切入点，基于避让系统核心模型(安全距离模型)展开对比分析与仿真计算，以期能够为汽车紧急避撞系统设计和优化工作的顺利进行提供帮助.

2 制动控制模型

基于横向动力学视角对汽车行驶极限状态的定义如下：车辆转向角对应传递函数以及横摆角速度均不在正常范围内，则表明汽车处于极限的行驶状态，即线性系统状态.由此可见，除特殊情况外，均可用线性二自由度模型对汽车所处状态进行判断.结合现有研究及所得结论可知，横摆角理想速度可经由以下公式加以表达：

其中，δf代表前轮转角，m代表汽车整体质量，vx代表纵向车速，a代表质心与前轴间距，b代表质心与后轴间距，Cf代表前轴对应侧偏刚度，Cr代表后轴对应侧偏刚度.

若汽车处于均匀运行状态，则横摆角理想速度和前轮转角的关系为线性关系.笔者出于对侧向运动进行精准控制且为日后设计控制器相关工作提供便利的考虑，将质心侧偏角做如下定义：

βd=0

由于横摆角速度与路面附着系数存在着明显的约束关系，因此，被用来对最大值进行表达的公式应为：

3 转向控制模型

对转向控制率进行有效设计的前提是建立转向控制模型，而建立转向控制模型所考虑的主要因素是横摆运动以及侧向运动，故建立转向控制模型如下：

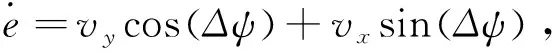
ep=e+xpsin(Δψ),Δψ=ψ-ψr

4 安全距离模型

关于智能汽车适用紧急避撞系统，要想使其发挥出应有作用，不仅要考虑上文提到的制动控制模型和转向控制模型，还要对安全距离引起重视，且安全距离模型对系统开发所具有的意义更为重大.本文将对该模型做详细叙述，供相关人员参考.

4.1 建立质点模型

4.1.1 建立模型

主动避撞系统所使用的控制策略，通常以制动和转向为主，其中，低速行驶的车辆更适合采用制动方式避撞，若车辆处于高速行驶状态，因其转向方式避撞对纵向安全最小距离的要求较制动方式避撞更低，则应优先选择转向方式避撞.基于转向方式避撞所制定的控制策略，通常会对两种情况加以考虑，分别为：一是换道后车辆保持稳定，侧向速度为0；二是换道后车辆有侧向速度存在[3].国内学者在考虑多方因素后，得出以下结论：

1)就高速行驶的车辆而言，要想使制动避撞取得应有效果，通常要有较大纵向距离提供支撑；

2)根据其他避撞方式对纵向距离所提出的要求，从大到小分别是转向避撞方法(a)(如图1所示)、转向避撞方法(b)(如图2所示)，但要注意一点，就是转向避撞方法(b)对车辆侧向位移所提出要求，通常较其他避撞方式更大.

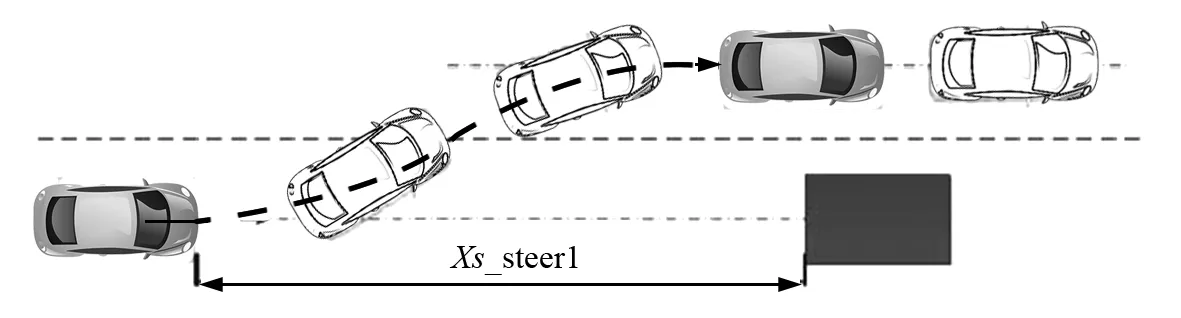
图1 转向避撞方法(a)

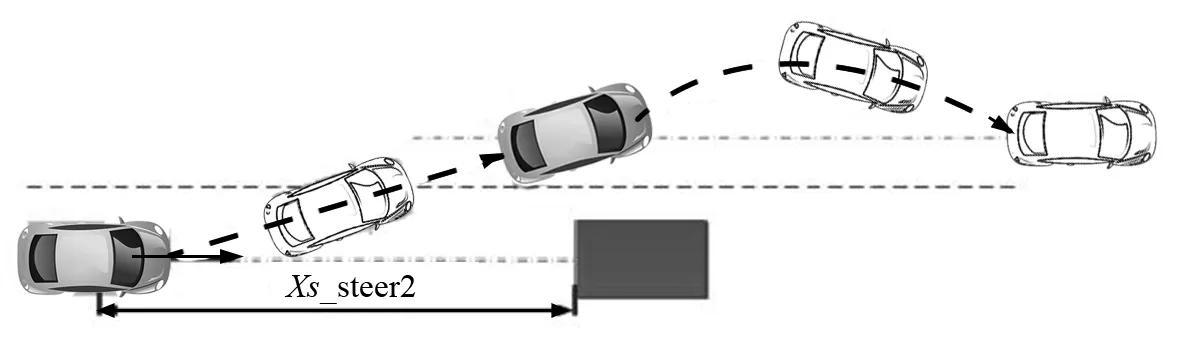
图2 转向避撞方法(b)

笔者出于不同避撞方式对纵向距离最小值所提出的要求，进行定量分析考虑，通过制动结合转向的方式，建立质点模型，其示意图，如图3所示.

图3 避撞质点模型

图3中地面坐标系设为XOY，车辆的坐标系设为xoy，基于地面坐标系XOY汽车运行的轨迹方程如下：

其中，m代表整车质量，ψ代表车辆航向角，Fx代表轮胎沿x轴向车辆质心所施加外力，Fy代表轮胎沿y轴向车辆质心所施加外力.

随后，结合牛顿第二定律以及轮胎所表现出的物理特性，可得到以下不等式：

ax,max≤ug

ay,max≤ug

其中，ax代表纵向加速度，ay代表侧向加速度，ax,max代表纵向加速度的最大值，ay,max代表侧向加速度的最大值，u代表路面附着系数，g代表重力加速度实际数值.

将状态变量ζ=[X,Y,vx,vy]引入，并将系统输入的u取值设定为u=[Fx,Fy]，便可得到如下用来对避撞状态加以表达的方程：

4.1.2 提出约束条件

预设避撞前，车辆状态满足：X(0)=X0；Y(0)=Y0；vX(0)=vX0；vY(0)=vY0的条件.避撞后车辆状态满足：X(t)=Xt；Y(t)=Yt；vX(t)=vXt；vY(t)=vYt的条件.预设初始时刻系统状态是[0,0,vx,0].要想使车辆避撞对纵向距离所提出要求达到最小，关键是要通过计算系统输入u的方式，确定Xt的最小解.

笔者计划采用不同方式对避撞操作进行操控.简单来说，方法一是制动避撞，方法二是转向避撞方法(a)，方法三是转向避撞方法(b).在确定约束条件并输入后，即可依托现有软件完成相关计算，具体约束条件，如表1所示.

表1 现有避撞方式对应系统输入及约束条件

4.1.3 模型分析

在车速不同的前提下，借助仿真平台对上述避撞方式处于高附着路面/低附着路面的优化做求解处理.研究表明，高速行驶车辆转向避撞对纵向距离所提出的要求，通常较制动避撞所提出的要求更低.例如，车辆以快于75 km/h的速度行驶时，采用转向避撞(a)进行避撞，可保证车辆安全的距离较制动避撞更小，若以侧向位移是3.5 m为约束条件，并采用转向避撞(b)进行避撞，在车速超过53 km/h的前提下，可保证车辆安全的距离较制动避撞所需距离更小[4].此外，还能得出以下结论：越低的路面附着性，越快的行驶速度，越能取得明显的制动效果.在条件完全相同的前提下，转向避撞(a)对安全距离的要求略高于转向避撞(b).

4.2 建立规避模型

4.2.1 规划参考路径

经由质点模型分别计算并分析上文提到转向避撞、制动避撞及综合避撞，确定参考路径.这里要明确一点，车辆和质点存在一定的差异，前者的本质是物理模型.因此，仅凭借质点模型对车辆安全距离进行估计，通常难以保证所得结论不存在误差.这也表明，即便用质点模型对避撞系统进行初步设计有理论支持，但要想使安全距离更精确，设计人员还要对车辆外形及尺寸加以考虑，并提前确定规避路径.

在满足一般性条件的前提下，根据转向规避情况对参考路径做出规划.预设转向避撞前车辆状态为匀速直线行驶，且纵向位移、侧向位移、初始侧速度、纵向加速度均为0，障碍物处于静止状态.设计人员应对侧向速度/侧向加速度的数值加以考虑，利用五次多项式对参考路径进行科学规划.

将车辆初始坐标设为(x0,y0)，终点坐标设为(xt,yt).一般来说，车辆避撞后，其纵向位移xt=b，侧向位移yt=a，纵向移动距离由质点模型进行求解：

其中，ci代表c1到c5的拟合系数.

通过计算可得到如下参考路径：

图4所示是初始速度为80 km/h的车辆基于高附着路面，经由避撞方式(a)/避撞方式(b)展开避撞试验所得轨迹和曲率[5].由图4所传达信息可知，虽然避撞方式(b)对纵向距离的要求略低于避撞方式(a)，但也存在曲率更大的问题.

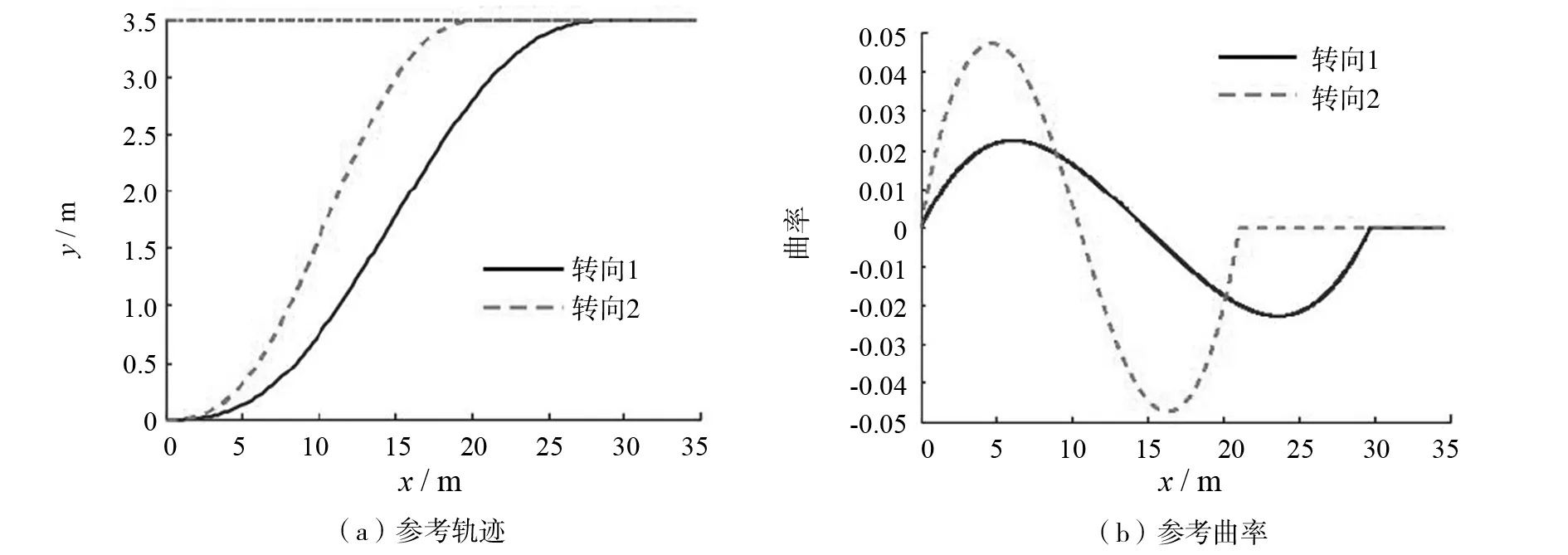
图4 不同避撞方式的轨迹与曲线

4.2.2 规避模型分析

笔者出于减小建模和降低分析难度的考虑，预设前车和本车拥有相同的外形及尺寸，两车的宽度、质心与轴的距离均是2 m.另外，为避免避撞过程中车辆和前车发生刮擦，还要对约束车辆外形及尺寸的条件加以考虑，并保证约束条件满足一般性要求.

制动避撞和转向避撞的主要区别是：前者只需要对车辆质心和前轴间距离加以考虑，后者的复杂程度更高，既要对上文所规划参考的路径加以考虑，还要与约束条件所提出的要求相符.现阶段，基于约束条件所开展的研究，其结论主要集中在包络圆假定和矩形安全区假定两方面.本文所采用约束条件为：车辆质心顺利通过障碍物的后上方时，由于实际轨迹和参考路径存在偏差的情况难以避免，因此，只需确保车辆质心和最近障碍角点的间距较安全距离更大即可.例如，在左转向避撞时，车辆质心在障碍角点上方，此时，二者间距至少应当等于1/2车辆宽度和安全距离d相加所得总长度，若d的取值是0.5，可得出下列关系式：

其中，wB代表车辆宽度.

对上述关系式进行联立，可对A点坐标进行求解，A点x坐标就是满足约束条件的纵向距离的最小值.

仿真1：基于高附着路面这一前提条件，车辆以80 km/h和100 km/h的速度行驶，由转向避撞(a)对参考路径所取得避撞效果加以分析，得出结论如下：在考虑约束条件的前提下，相较于质点模型，两车的安全距离最小值均有所减小.

仿真2：基于高附着路面这一前提条件，车辆以80 km/h的速度行驶，由转向避撞(a)/转向避撞(b)对参考路径所取得避撞效果加以分析，得出结论如下：在考虑约束条件的前提下，转向避撞(b)减小安全距离最小值的效果更加明显.

仿真3：基于低附着路面这一前提条件，车辆以80 km/h和100 km/h的速度行驶，由转向避撞(a)/转向避撞(b)对参考路径所取得避撞效果加以分析，得出的结论与仿真1和仿真2大致相同.

仿真4：如果以避撞方式不同为前提，初始速度不同的车辆，避撞所需纵向距离最小值往往与路面条件有直接联系.实验表明，在转向联合制动的前提下，与纯转向相比，避撞所需纵向距离最小值有所减小.而以约束条件为依据所进行实验，相较于质点模型，车辆做到安全避撞所需纵向距离的最小值，同样有明显的减小趋势.

5 结论

通过上文的分析可得出以下结论：1)无论是质点模型还是对车辆外形与尺寸加以考虑所建立模型，可取得最佳避撞效果的方式均为制动+转向，这是因为该方式对纵向距离的要求较其他方式更低.2)由参考轨迹曲率可知，虽然转向避撞(b)较避撞方式(a)对纵向距离的要求更低，但会出现避撞程度更为剧烈的问题.3)对车辆外形与尺寸加以考虑的模型，其实际意义更符合研究目标.4)现有避撞方式均可为相关系统的设计及开发提供参考，避撞策略的选择依据，主要是设计人员自身倾向和约束条件，例如，障碍物速度及所处位置.