人工冻结砂土热力耦合模型分析

高亚飞，曹虎生，麻世垄

(1.陕西省一八五煤田地质有限公司，陕西 榆林 719000;

2.安徽理工大学土木建筑学院，安徽 淮南 232001)

0 引 言

在工程施工中，土体的冻胀、融沉会给道路和建筑物造成很大的危害，有必要对冻土施工中土体的冻胀融沉进行研究。何敏等[1]以饱和冻土多孔介质传热理论为基础，运用克拉伯龙方程揭示温度梯度对冻结区水分迁移的影响规律，简化数学计算模型，建立了实用性的水热力耦合数学模型；白青波等[2]基于热传导理论和达西定律理论，通过Comsol软件二次开发，运用偏微分方程对水热耦合求解，实现冻土水分场和温度场全耦合数值计算；刘建军等[3]建立多年冻土区的水热力耦合模型，考虑了水分迁移和冰水相变的影响，运用Comsol数值计算软件对多年冻土进行水热力耦合计算，得出了多年冻土的位移曲线；韩建泽[4]基于海相软土降温冻结过程中出现的二次相变现象，对温度场、水分场、应力场和盐分场控制方程进行修正，建立了水-盐-热-力四场耦合的人工冻结海软土冻胀预报模型；王永涛等[5]基于饱和青藏粉土在不同温度条件下的单向冻结试验，对冻结过程中冻胀速率和冻结厚度的影响因素进行研究分析，得出影响土体冻胀率变化的内在机理为土样冻结过程中由冰透镜体分凝冰所导致的未冻区固结和已冻区冻胀共同作用的结果；李锐阳[6]通过冻土理论和水热迁移的试验模拟及双圈管冻结模型分析，对深厚地层土壤水热迁移进行系统分析；高建强等[7]在室内单向冻结试验的基础上，分析了在考虑覆盖层和补水条件下，温度、土质和温度边界条件对非饱和粗颗粒填料冻胀特性的影响。

大多数学者认为，引起土体的冻胀融沉主要来源于冻结土层内部水分迁移以及因水分迁移而导致的水分重分布。然而，水分重分布主要为冰水相变，导致冰水相变的主要因素为土体内部的冻结温度。本文基于前人研究的基础，研究人工冻结砂土的热力耦合机理，通过Comsol Multiphysics数值计算软件中多孔介质传热模块、固体力学模块，建立多物理场耦合模型，模拟不同冻结温度下的饱和砂土内部冻结温度场的分布及冻胀量大小，对采用人工冻结法施工的工程具有一定的参考意义。

1 冻结砂土热力耦合分析

1.1 热力耦合模型基本假定

假设砂土在未冻结以及冻结状态下均为连续、各向同性的弹性材料；冻结砂土内部被液态水和固态冰填满。

冰水相变的热量的改变仅以热传导的方式进行，忽略热辐射和热对流；试验为不补水试验，冰水相变只考虑原含水率；温度载荷以实际试验循环的冻结温度直接加在模型顶部边界；数值计算模型两侧面边界为对流换热边界条件，底部为绝热边界条件；在力学场中，模型顶面为自由边界，两侧面为辊支撑约束，底部为固定约束。

1.2 温度场控制方程

在未冻结区，二维温度场的控制微分方程为

(1)

在冻结区，二维温度场的控制微分方程为

(2)

冻土中未冻水相变释放的相变潜热为

(3)

式中，Tu和Tf分别为未冻结区与冻结区的温度；ku和kf分别为未冻结区与冻结区的导热系数；Cu和Cf分别表为未冻土与冻结土的比热容；q0为源项；Q为相变潜热；θi为体积含冰率；t为时间；pi为冰的密度；L为冰水相变潜热，为335 kJ/kg。

初始条件为

T|t=0=T0

(4)

式中，T0为土体的初始温度。

模型中，直接以试验循环的冷媒剂的温度加在试样的顶部边界，因此顶部边界条件为

T|y=yc=Tc(t)

(5)

式中，yc为模型上边界的纵坐标；Tc(t)为循环的冷媒剂的温度。

模型中，两侧面考虑对流传热的影响，有对流换热边界条件，即

q0=h(t)×(Text-T)

(6)

式中，h(t)为对流换热系数；Text为外部温度。

以上式(1)～(6)构成二维冻结温度场的定解问题。

1.3 热力耦合控制方程

热力耦合情况下的力学场为平面应变问题，其微分控制方程为

(7)

(8)

(9)

式中，σx为平面x方向正应力；εx为平面x方向正应变；σy为平面y方向正应力；εy为平面y方向正应变；τxy为平面剪应力；εxy为平面剪应变；T为温度差；E(T)为考虑温度变化的土体弹性模量；u为泊松比；α为热膨胀系数。

2 数值模拟

试验所用砂为榆林某路基砂土，试验试样为直径50 mm、高度100 mm的圆柱体。为简化计算，数值计算模型采用二维平面模型，所建试样模型尺寸为宽50 mm、高100 mm的矩形，网格划分采用自由剖分三角形网格，上下边界为试验边界条件，左右边界考虑相应的热散失。几何模型由1个域、4个边界、4个顶点组成。以试样低端为0 ℃面，在20、40、60、80 mm处埋设温度探针。网格划分见图1。

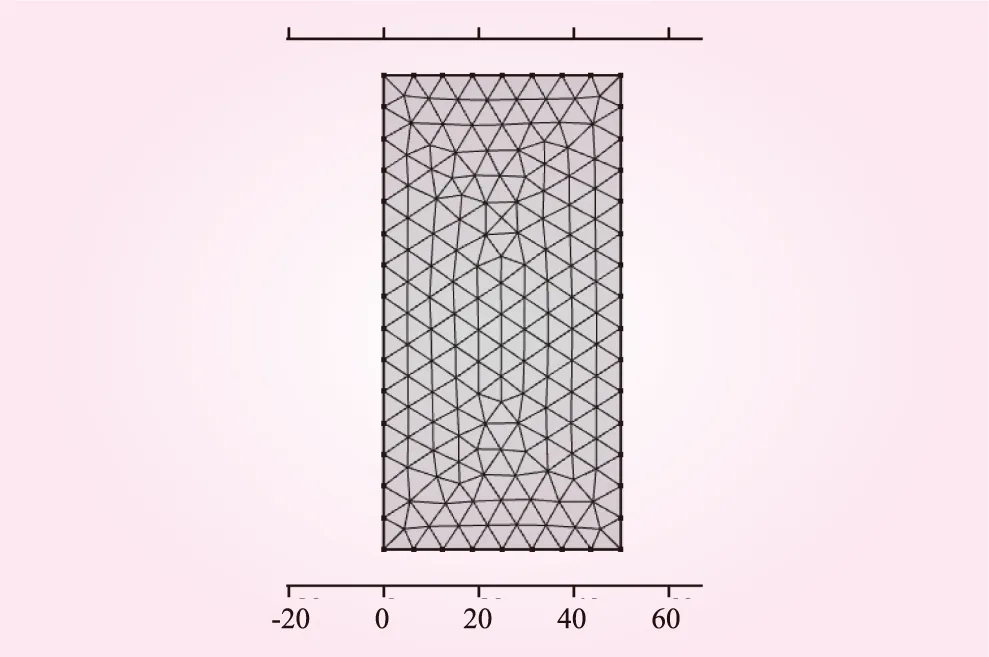
图1 网格划分(单位：mm)

数值模拟计算时，试样上端为冷端，试样下端为暖端。通过数值模拟计算，得到试样在不同冷端温度下试样温度达到稳定时的温度云图，见图2。从图2可知，初始含水率一定时，在上部不同冷端温度下，随着冷端温度的降低，试样沿高度方向温度区域划分更明显。因冻结端面向下传递的冷量受土体深度影响，当土体深度一定时，随着冷端温度的降低，热阻造成的冷量损失减小，故土层温度稳定时整体温度偏低。

图2 不同冷端温度下试样温度云图(单位：℃)

在数值模拟计算过程中，通过时间计算步长可知，当冷端温度为-5 ℃时，试样低端温度达到0 ℃所需时间为128 h；当冷端温度为-10 ℃时，试样低端温度达到0 ℃所需时间为50 h；当冷端温度为-15 ℃时，试样低端温度达到0 ℃所需时间为38 h，说明随着试样冷端温度的降低，试样低端温度降至0 ℃所需时间变短。这是因为随着冷端温度的降低，冻结端面施加的负温增量逐渐增大，单位时间内土体冻结深度变大，故达到0 ℃所需时间变短。

基于热力耦合模型，本文所建立的模型试验不考虑外部荷载作用，此处主要以冻胀量来描述热力耦合中热交换对力的影响。通过数值模拟计算，得到在不同冷端温度下试样温度达到稳定时的位移场云图，见图3。从图3可知，在无外界水源补给的试验条件下，当冷端温度为-5 ℃时，试样位移场达到稳定时土体的冻胀量为1.49 mm；当冷端温度为-10 ℃时，试样位移场达到稳定时土体的冻胀量为2.34 mm；当冷端温度为-15 ℃时，试样位移场达到稳定时土体的冻胀量为1.91 mm。这是因为随着冷端温度的降低，试样内部未冻水含量降低，导致

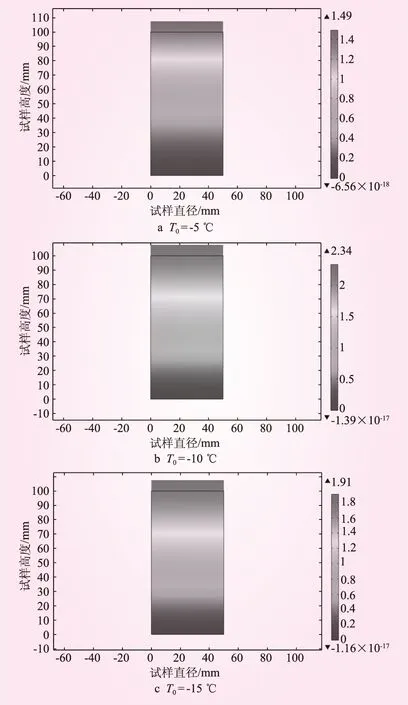
图3 不同冷端温度下试样冻胀量云图(单位：mm)

冻结时产生的冰晶体数量相应增长，故法向冻胀力增长，从而使土体的冻胀量增大；但当冻胀力达到一定值时，土体内部的冰晶体破坏，从而土体的冻胀量减小。实际工程中，由于存在地下水的补给条件，冻结土体的冻胀性更明显。

3 数据分析

根据温度和冻胀量云图，选取-10 ℃的各测点模拟值和试验值进行对比。试样测点温度实测值与模拟值对比见图4。从图4可知，试样测点温度实测值和数值模拟值变化规律一致，距离冷端的距离越近，土体降温速率越大；距离冷端越远，土体降温速率越小。在冻结试验前10 h，测点实测温度和模型模拟温度下降速率最大，当冻结时间达到48h后，各测点实测温度和模型模拟温度都逐渐趋于稳定。对比试验值和模拟值发现，模拟得到的稳定温度值略低于试验值，但整体效果较好。因试验过程中，试样受周围环境的影响比较大，试样一部分能量用于热交换，故在测点处模型模拟值较试验值温度低。

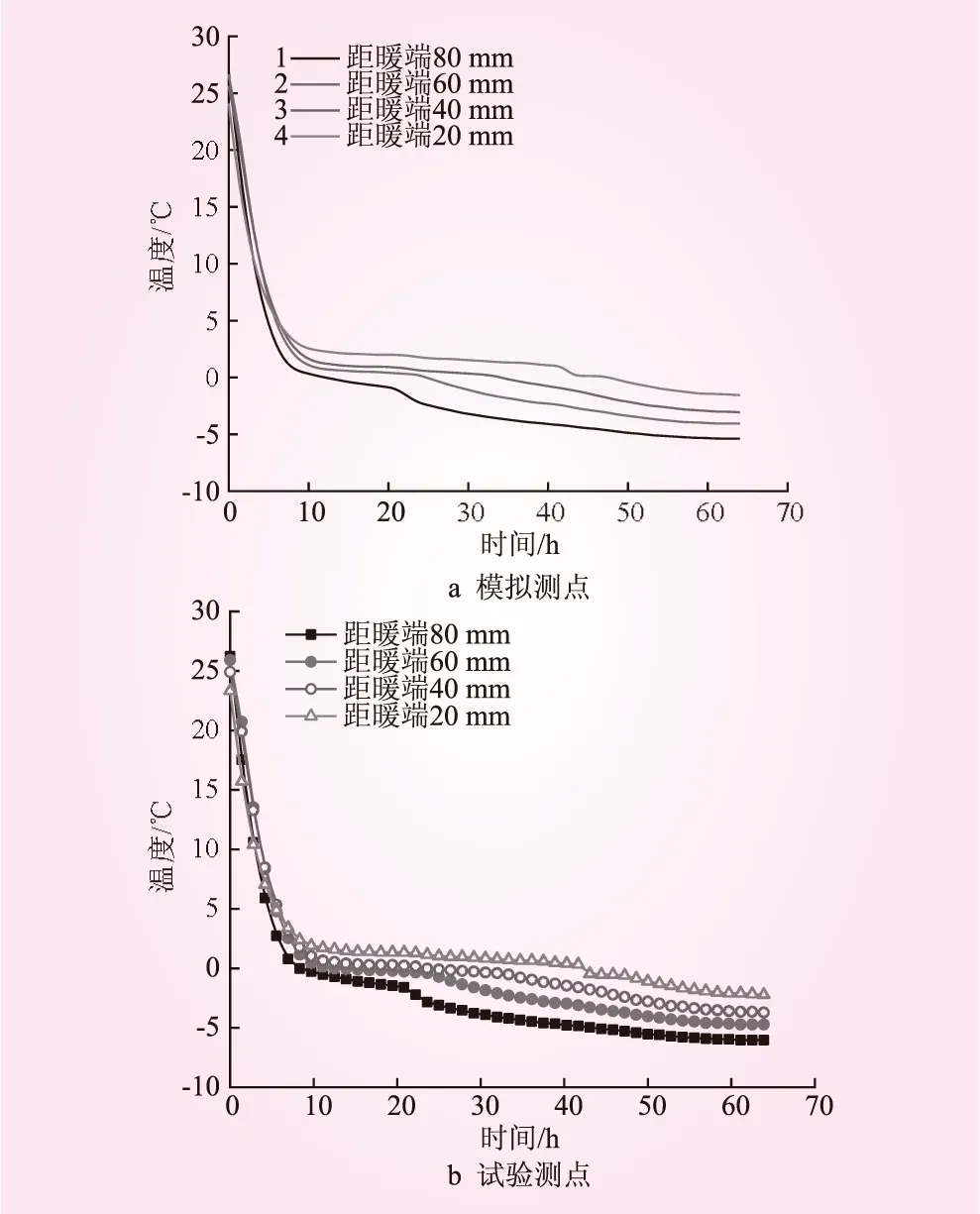
图4 试样测点温度实测值与模拟值对比

试样实测冻胀量与模拟冻胀量对比见图5。从图5可知，热力耦合模拟值和实际测量值变化趋势一致，热力耦合模型较好地模拟了冻结过程中冻胀量的变化趋势。在冻结时间的前16 h，冻结砂土土体冻胀量随时间的增大几乎呈线性增大；在16 h以后，冻胀量变化几乎呈波浪变化并逐渐趋于定值。表明所建立的模型适用于榆林某路基砂土，所建模型合理。

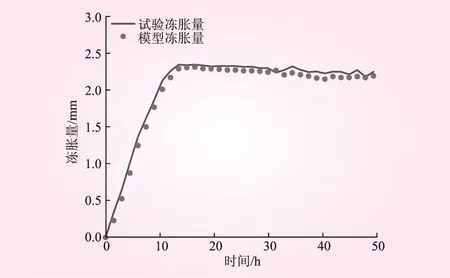
图5 试样实测冻胀量与模拟冻胀量对比

4 结 语

本文通过能量守恒定律和多孔介质传热理论，分析砂土在单向冻结时试样内部热量分布情况；运用固体力学理论，分析土体在自重情况下冻胀量的大小；运用广义胡克定律和克拉伯龙方程，考虑砂土在单向冻结时土体内部的热力耦合。榆林某路基砂土热力耦合模型模拟结果和试验实测结果对比表明，此模型能很好地模拟土体在冻结过程中土体内部的热量变化和冻胀量情况，可应用于工程实际。