胶凝砂砾石抗压强度的预测及分析

任国峰，关 炜，陈守开，柴启辉

(1.安阳市万金渠管理处，河南 安阳 455000；2.水利部南水北调规划设计管理局，北京 100038；3.华北水利水电大学水利学院，河南 郑州 450045；4.河南省水环境模拟与治理重点实验室，河南 郑州 450045；5.水资源高效利用与保障工程河南省协同创新中心，河南 郑州 450045)

0 引 言

胶凝砂砾石(Cemented Sand and Gravel，CSG)坝是介于碾压混凝土坝和面板堆石坝之间的新坝型，在优化结构布置、节约工程投资、保护生态环境等诸多方面具有显著的优点[1-2]。CSG是将胶凝材料(主要是水泥和粉煤灰)、水、河床原状砂砾石或开挖废弃料等材料通过简易设备拌和后得到的一种新型筑坝材料[3]，作为结构性材料，其力学性能一直是国内外学者研究的重点。

孙明权等[1]通过抗压强度试验分析用水量和砂率对CSG抗压强度的影响，得出最优砂率为0.2，最优水胶比范围为0.95～1.35；柴启辉等[4]通过强度试验也得到了类似结论；Yang等[5]通过三轴压缩试验，提出CSG的强度准则与胶凝材料含量、骨料含量和级配的抗剪强度有关；杨世锋等[6]通过三轴试验的应力应变曲线得到了CSG材料抗剪强度指标值，并建立了与单轴试验力学指标之间的对应关系；Yokotsuka等[7]结合Nagashima拦砂坝工程，开展了单位用水量对CSG性能的影响研究，建议实际应用中VC值控制在5～20 s为宜。通过上述文献的分析，发现现阶段多数研究是围绕CSG原材料掺量变化展开的，而关于CSG性能预测方面的研究涉及较少。

随着计算机技术的发展，人工神经网络作为一种模拟人脑神经元网络的运算模型，被广泛应用于各行业。BP神经网络作为人工神经网络的一种，因其拥有较高的预测精度且方便快捷，近年来在混凝土性能预测方面取得了较为丰富的研究成果。陈守开等[8]应用BP神经网络建立了基于渗透性能和强度性能的再生骨料透水混凝土性能预测模型，预测值平均相对误差均在10%以内；李扬等[9]采用BP神经网络模型对复合盐侵蚀-干湿交替作用下混凝土相对动弹性模量的损失率进行了定量预测，平均误差百分比为2.08%； Alshihri等[10]建立BP神经网络模型来预测轻质混凝土的抗压强度，其预测值的平均相对误差为1.987%；Ni等[11]也通过神经网络来预测混凝土的28 d抗压强度，绝对误差最大为3.45 MPa，其对应的相对误差为5.86%。本文基于Z-score标准化方法对CSG抗压强度数据进行异常值的判别与剔除，在此基础上应用BP神经网络模型分析CSG抗压强度的可预测性以及预测的结果，为CSG的无损检测与应用提供参考与借鉴。

1 试验材料及配合比设计

1.1 试验原材料

(1)水泥采用河南多样达水泥公司生产的P·O 42.5普通硅酸盐水泥，其化学成分及物理力学性能见表1。

表1 水泥基本性能

(2)粉煤灰选用郑州热电厂Ⅱ级粉煤灰，其基本性能见表2。

表2 粉煤灰基本性能

(3)骨料。细骨料采用汝州市北汝河料场河沙，其细度模数经测定为2.58，属于中砂。砂砾料采用汝州市北汝河料场砂砾料，含砂率为22.11%，经分级筛分后分为150、80、40、20 mm，以供骨料级配的选择。

1.2 配合比设计

试验参照超贫胶材料研究成果和SL 678—2014《胶结颗粒料筑坝技术导则》进行设计，材料表观密度为2 350 kg/m3，其中部分数据的配合比如下：

(1)水泥用量。水泥是影响CSG材料性能的主要因素，在研究水泥用量对CSG强度的影响时，以水胶比1.0为前提，胶凝材料总量为80、90、100 kg/m3，砂率分别为0.1、0.2、0.3、0.4，水泥用量为50 kg/m3和40 kg/m3。

(2)粉煤灰用量。在研究粉煤灰掺量对CSG抗压强度的影响时，以水胶比1.0为前提，水泥用量为50 kg/m3和40 kg/m3，砂率为0.2、0.3、0.4时，粉煤灰掺量为50、40 kg/m3。

(3)砂率。砂率的大小会影响试件的密实程度和材料的粘结性，在研究砂率对CSG抗压强度的影响时，同一水泥用量、粉煤灰掺量、水胶比情况下，砂率分别为0.1、0.2、0.3、0.4。

(4)水胶比。水胶比是影响CSG材料性能的关键指标之一，在研究水胶比对CSG抗压强度的影响时，同一水泥用量、粉煤灰掺量、砂率情况下，水胶比分别为1.0、1.2、1.4。

(5)粗骨料级配。骨料级配为二级配，5～20 mm骨料与20～40 mm骨料比值设定为4∶6。

按照试验规范要求，对尺寸为150 mm的二级配标准立方体式样进行制备，具体方法与试验流程见参考文献[3]，达到养护龄期后借助立方体抗压强度试验机测得其抗压强度值。

2 数据处理及预测

2.1 样本数据

本文构建的CSG 28 d抗压强度样本数据集(见图1)，共117组，其中部分数据来源于试验获得的CSG力学性能的实测数据，共40组；其余部分来源于文献2、12-14的试验数据，以增加数据的普遍性和多样性。在该样本数据集中，CSG抗压强度的最小值为1.00 MPa，最大值为17.7 MPa，且主要分布区间集中在1～10 MPa，约占总样本数的94.9%。

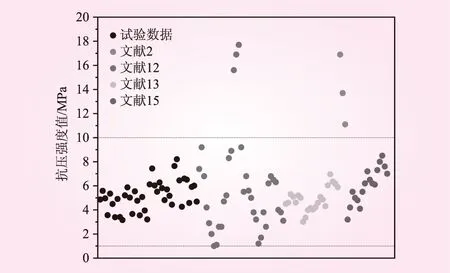
图1 CSG 28 d抗压强度数据集

2.2 Z-score标准化法

Z-score标准化处理目的是从大量的、无序的数据中抽取对相关问题有价值、有意义的数据。在所建立的抗压强度数据集中，由于数据来源不同，CSG材料的制作工艺、配合比等之间存在一定的差异，因此需要对过大或过小的数据(即异常值)进行判别并剔除，以降低对数据的预测结果产生影响。

Z-score标准化以正态或近似正态的数据分布形式为前提，是基于原始数据的均值和标准差进行处理计算的线性标准化方法，可以用来检测参数异常值。其值不受原始测量单位的影响，算法简单方便，并可接受进一步的统计处理，其表达式为

(1)

式中，zi为计算结果；xi为原始数据；μ为总体数据的均值；σ为总体数据的标准差。当|zi|>3时，可判定为异常值并选择剔除。

本文借助Q-Q图法对数据的分布形式进行检验。Q-Q图是用图形来描述数据的一种方法，可对数据的正态性假设进行验证，它是用样本数据分位数和某假定分布形式时的分位数进行比较的散点图[15]，当图形分布与所给直线较为接近时，即可认为符合该假设分布。

由图2可知，相比较指数分布，CSG 28 d抗压强度数据更符合正态分布的规律特征。如图2a所示，CSG抗压强度除了在双尾处存在个别离散性较大的点，其余部分均基本与斜率为1的直线较为接近。通过计算得到CSG 28 d抗压强度样本数据的均值为5.65 MPa，标准差为2.84 MPa，并结合式(1)确定其zi值。

图2 抗压强度值各假设分布Q-Q图

zi值计算结果如图3所示，计算获得zi值大于3的分别为3.50、3.95、4.24和3.96，其对应的原值分别为15.60、16.90、17.70、16.91 MPa，故选择将该数据进行剔除。

图3 zi值分布

2.3 BP神经网络

BP神经网络模型是由输入层、输出层和隐含层组成，相邻层之间各神经元互相连接，单独层的各神经元相互独立。其基本原理是当输出层的输出值与期望值不匹配时，通过误差反向传播来修正网络的权值和阈值，使输出值与期望值之间的误差平方在阈值范围内。

2.3.1 预测样本

根据2.2节的结果，剔除异常值后参与预测的总体样本为113组(见表3)。其中，训练组占总体样本数的75%，验证组和预测组都为总体样本的15%。通过程序随机抽样分配数据，保证数据预测具有代表性。

表3 BP神经网络预测样本数据

2.3.2 网络模型构建

分别选取水泥用量、粉煤灰用量、水用量、砂用量、砂砾料用量、砂率、水胶比和水灰比8个关键指标作为输入层，28 d抗压强度作为输出层建立CSG抗压强度预测模型，隐含层为单层，隐含节点数采用试凑法确定，即

(2)

式中，h为隐含节点数；m、n分别为输入层和输出层节点数；a为调节常数，取值范围为1～10。经过多次试算，当a为10时，训练效果最好，即构成8-13-1的预测模型结构，其网络模型的拓扑结构如图4所示。

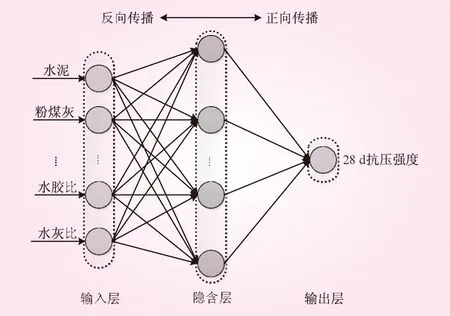
图4 BP网络拓扑结构示意

采用Matlab软件自带工具箱来实现网络模型的训练，隐含层传输函数采用tansig函数，purelin函数作为输出层函数，训练函数采用BP算法中的trainlm函数，其他参数选择默认值。另外，由于各个参数的单位以及范围存在较大差别，会影响网络的初始化效果，也会导致网络难以收敛，而且网络中非线性激活函数的值域是限制在[-1，1]或[0，1]之间，网络训练的目标数据也应当映射到激活函数的值域内，以便很好地利用激活函数的区分度以达到较好的预测效果。基于此，需要对数据进行归一化处理，使网络能以较快的速度收敛并得到较为精确的结果，其公式为

(3)

式中，y为归一化后的数值；xmax、xmin分别为所在数据列的最大值和最小值；x为原始数据。

2.3.3 预测结果分析

表4为28 d抗压强度的预测结果，图5为相应的结果对比图。其中，绝对误差为0.01～1.19 MPa，相对误差为0.21%～23.01%。

图5 28 d抗压强度结果对比

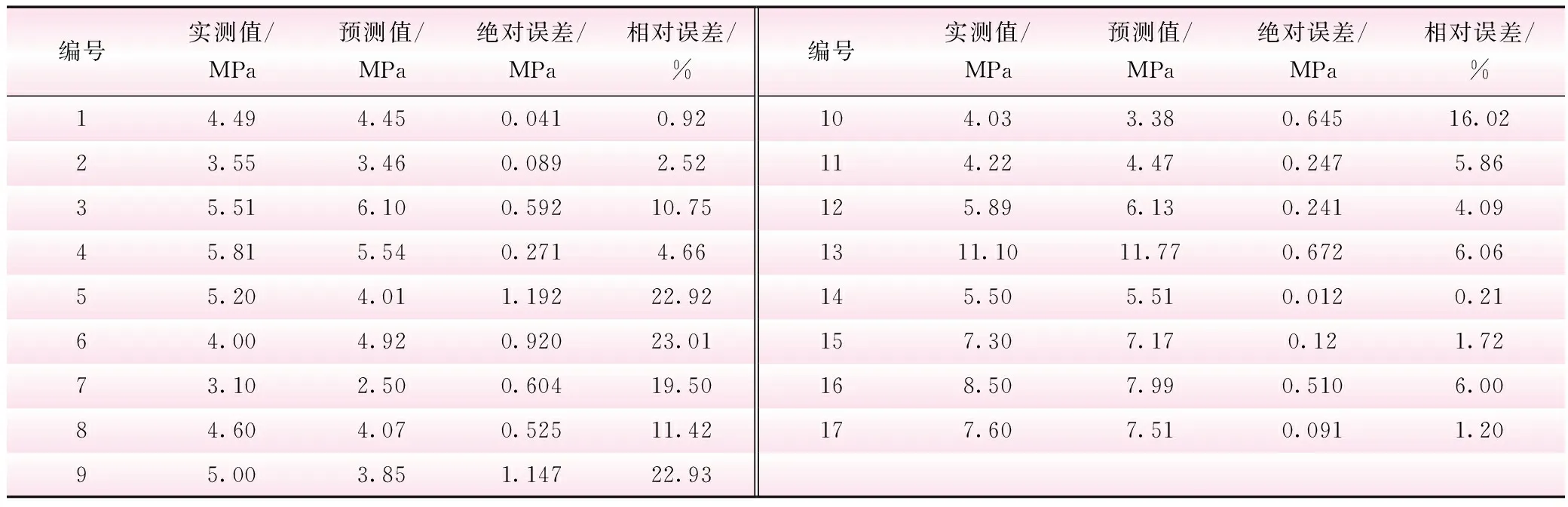
表4 28d抗压强度误差

由预测结果可知：①CSG抗压强度具备可预测性，且预测的精度较高，平均相对误差和平均绝对误差分别为9.40%和0.47 MPa，同时也说明了BP神经网络模型能够在CSG材料领域得到较好的应用；②从参与模型预测的CSG抗压强度数据集来看，数据来源形式不同，主要体现在试验条件、材料、工艺等方面的差异，而经由BP神经网络模型的训练与修正，依然能够获得较高的精度，说明该模型对于多源数据的预测具有一定的适用性。此外，从图5中也发现了个别数据误差偏大的情况，如第5、6组，其相对误差分别为22.92%和23.01%，绝对误差分别为1.19 MPa和0.92 MPa。分析形成误差的主要原因是由于BP网络模型自身存在一定的系统误差，以及在制备CSG试件的过程中产生的误差联合导致。

为进一步验证实测值与预测值总体有无显著性差别，本次研究采用比较平均值的配对样本T检验方法来进行分析。同一研究对象用2种不同的方法获得的数据或用一种方法处理前后的数据均可用配对样本T检验方法进行比较。本次检验的置信区间设置为95%，假设“实测值”与“预测值”的平均值相等，统计量t在显著水平0.05和自由度为16时，拒绝域为|t|>2.12，本次的结果为t=1.06，明显小于2.12，表明假设成立，且实测值与预测值的相关性达到了0.97，Sig值为0.31远大于0.05，所以在显著水平0.05条件下，尚不能认为实测值和预测值有差异，其具体结果见表5。

表5 配对样本T检验结果

3 结 论

(1)运用Z-score标准化法对经检验符合正态分布规律的CSG 28 d抗压强度数据集进行异常值的判别与剔除，发现存在4组异常值并进行剔除，其值分别为15.60、16.90、17.70 MPa和16.91 MPa。

(2)建立了基于BP神经网络方法的CSG抗压强度预测模型，预测结果显示CSG抗压强度具备可预测性，且预测值与实测值的吻合度较高，其平均绝对误差和平均相对误差分别为0.47 MPa和9.40%；最后运用配对样本T检验方法对实测值和预测值的差异性进行检验，发现两者相关性较高且误差较小，表明BP神经网络模型能够作为预测CSG材料性能的工具。