改进NSGA-II算法及监测天线部署优化研究
2021-11-12杜文占余志勇姜海滨
杜文占,余志勇,杨 剑,姜海滨
(1.火箭军工程大学 302教研室,陕西 西安 710025;2.火箭军工程大学 205教研室,陕西 西安 710025)
地面电磁辐射源监测装备的高效部署是全面可靠地感知电磁环境的基础。然而,地形复杂,建筑物、树木等障碍物分布杂乱,电磁信号可能被反射、散射和衍射,从而在传输路径上消散,对辐射源信号监测造成不利影响。MALON等[1]结合城市地形特点,以天线之间的距离为约束条件,给出了检测参数、天线数量和距离约束对监测装备准确性的影响。文献[2]提出了一种新的分布式并行多目标进化算法(Multi-Objective Evolutionary Algorithms,MOEAs)解决传感器网络在城市三维地形中智能部署的问题,并通过实际地形对该算法进行了验证。文献[3]将协同监测模型的多个指标归一化为一个综合评估指标,可靠性较低。陈涛等[4]提出了基于地理信息系统(Geographic Information System,GIS)的优化部署策略,根据地形复杂情况布设不同数量的电磁监测装备,有效避免了多径效应的影响,但覆盖冗余率过高。基于自适应遗传算法[5-6]将天线部署作为协同优化问题,对监测站覆盖范围和站点布局规划进行仿真,提高了电磁监测装备的覆盖率,但没有考虑障碍物对监测准确性的影响。
在大多数的研究中,地面天线的部署优化主要考虑静态环境下的覆盖率最大化,很少有针对避免障碍物影响和动态环境下高效部署的研究。当部署区域、天线位置等发生改变时,算法收敛的速度决定着天线重新部署的效率,因此需要提高算法响应动态变化的能力[7]。笔者以最大化覆盖率、最小化冗余率和覆盖区域内障碍物为目标构建模型,并通过改进NSGA-II算法在不同参考点数量和不同部署区域下分别对该模型进行了仿真分析。
1 问题描述
覆盖率和冗余率是评价监测天线部署效率的重要指标。实际地形中障碍物的存在会对天线的准确监测造成严重影响。战场环境中高温、噪音、气候变化等问题,干扰数据传输,导致链路断裂。因此,在部署时需要保证每两个天线间至少有一条通信链路并且具有较强的连接能力和可靠性。在本节中对目标函数和约束条件进行了介绍。
1.1 障碍物
在复杂的战场电磁环境下,电磁波难以在辐射源和监测天线之间直线传播。在传播过程中遇到障碍物(如建筑物、树木)时,辐射源信号被反射、散射、衍射或吸收。地理环境是一种客观存在,不同的地形地貌,如平原、丘陵、山地等影响着地面对电磁波的吸收或反射。当障碍物表面平滑且尺寸比信号波长大得多时,信号就会在障碍物表面发生反射或折射;当障碍物尺寸与信号波长相似或更小时,信号就会绕过障碍物继续传播,形成绕射。
是否存在障碍物、障碍物是否连续、障碍物相比于电磁波波长的大小等因素引起的多径效应(Multipath Propagation)会对监测天线相位和幅度产生影响,导致监测结果产生偏差甚至突变。文献[8]提出了估计辐射源和监测天线之间功率损耗的无线传播模型
(1)
其中,Lpl为辐射功率的路径损耗;μ∈[2,5]为路径损耗系数,自由空间中,μ=2,其他环境中,2<μ<5;d是发射源到接收端的直接路径距离;K为直接路径上障碍物的数量;α(i)和β(i)∈[0,1]分别为障碍物i的衰减指数和渗透率。β(i)i-1表明天线和障碍物之间的距离越小,对监测准确度的影响就越大。因此,在监测天线覆盖区域内的障碍物数量K越少,对准确监测辐射源的影响就越小。
1.2 覆盖率和冗余率
最大化天线覆盖率是有效监测未知位置的电磁辐射源的重要前提。假设每个天线的监测覆盖范围是一个半径为最大监测距离的圆,则检测概率可以定义为一个二元感知模型[9],如式(2)所示。假设监测天线数量为M,潜在辐射源数量为N,天线增益为0 dBi,则天线(m)监测到辐射源(n)信号的结果为
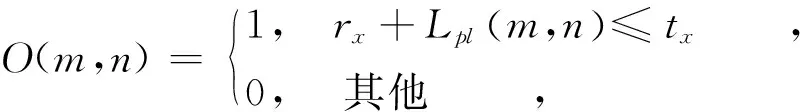
(2)
其中,rx为监测天线正确检测信号的信号强度,tx为辐射源信号强度,Lpl(m,n)为辐射源和监测天线间的路径损耗。
如图1所示,阴影部分面积为
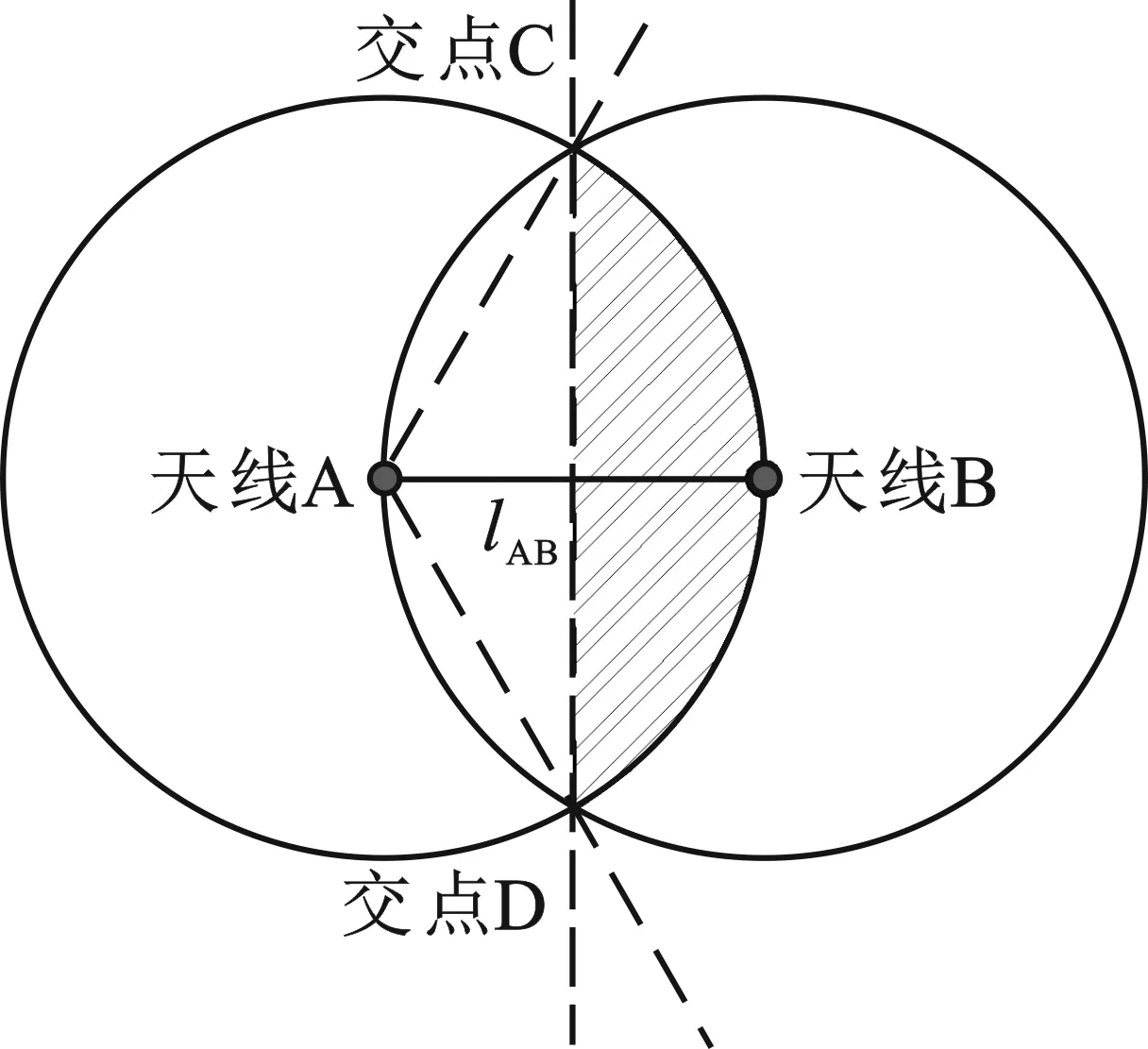
图1 计算阴影部分面积
SCBD=SACBD-SACD
(3)
其中,SACBD为扇形ACBD的面积,SACD为三角形ACD的面积。
计算冗余率,如式(4)所示,
(4)
其中,R为天线最大监测距离;t为lAB<2R情况的个数,lAB为天线A和B之间的距离。
根据式(5)计算覆盖率O,其中SROI为部署区域面积。
(5)
1.3 天线连通性
在M>1的情况下,天线需要交换数据,相互之间必须能够无线通信,形成监测网络以获得电磁态势评估。监测天线和辐射源的示例如图2所示。
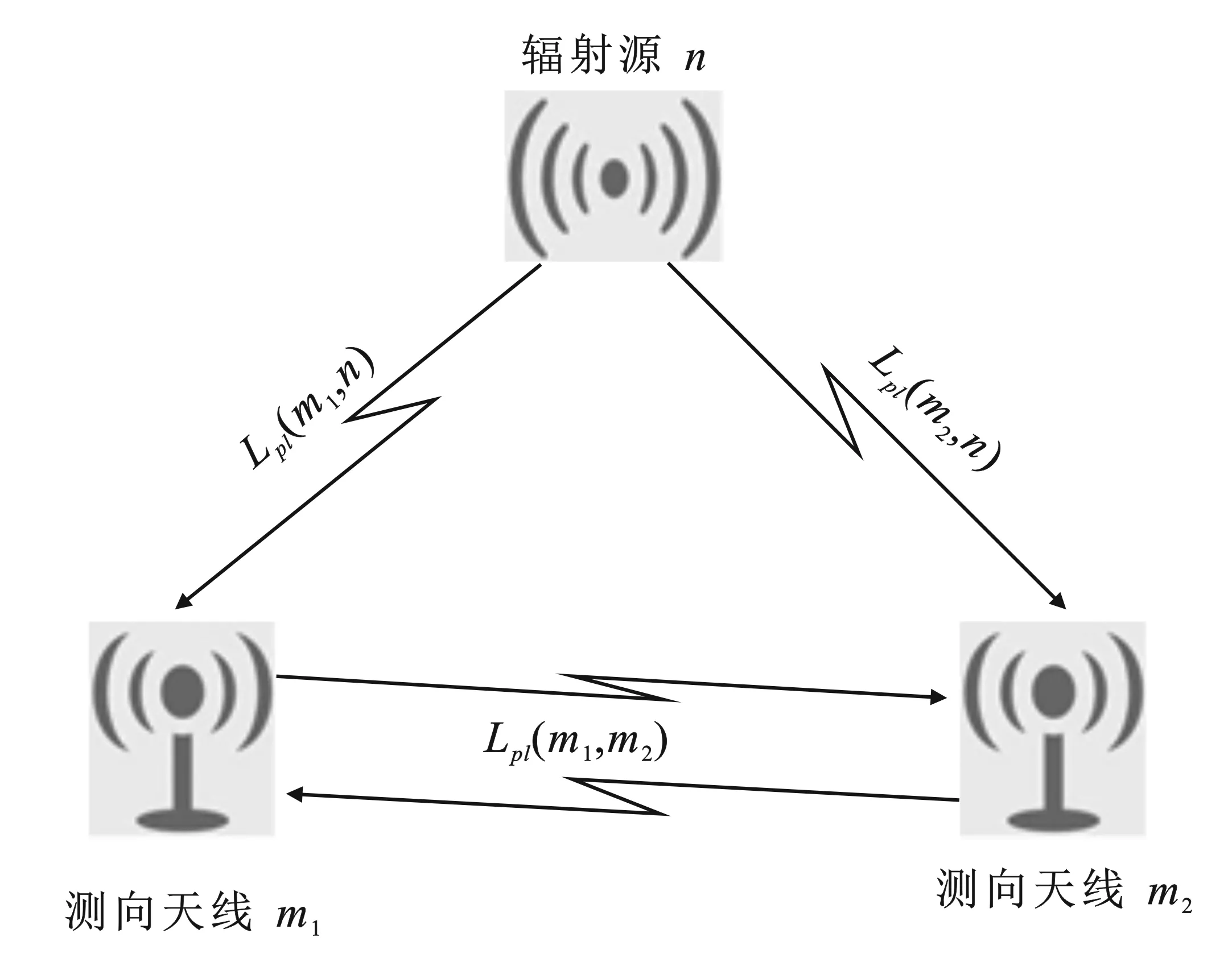
图2 测向天线和辐射源示例图
文献[1]中给出式(6)计算两个天线相互通信的能力:
(6)
其中,ry为监测天线m1接收信号强度,ty为监测天线m2发射信号强度,Lpl(m1,m2)为m1与m2之间的路径损耗。
部署M个天线时,根据式(7)计算天线间保持通信的平均连接距离:
(7)
其中,lm1m2为具有连通性的两个天线m1与m2间的距离,Ml表示天线间具有连通性的通信链路个数,lmax为最大通信距离。
1.4 多目标优化模型
多目标优化问题中的目标之间存在矛盾冲突,无法保证每个目标同时达到最佳值,即不存在能使所有目标都为最优的解,因此,解决方案将会是在均衡所有目标的基础上寻求最接近最优解的解。
在动态多目标优化问题(Dynamic Multi-objective Optimization Problem,DMOP)中,目标、约束或参数随时间而变化,动态帕累托最优前沿(Pareto Optimal Front,POF)和帕累托最优解集(Pareto Optimal Solution,POS)分别是关于目标空间和决策空间的非支配解的集合。当环境改变并且被检测到时,通常POS或POF也发生变化,影响DMOP的现有解决方案,所以目标是跟踪动态POF或POS。因此,必须提高算法收敛速度,在下一次改变发生前,尽快找到新部署方案。
多目标优化问题的数学模型为
(8)
决策变量为天线部署位置坐标,如下所示:
X=[(x1,y1),(x2,y2),…,(xm,ym)]T,(xi,yi)∈ROI,i=1,2,…,M,
(9)
其中,决策空间ROI(Region of Interest)为监测天线部署区域,上标T表示矩阵的转置。
2 改进NSGA-II算法
NSGA-II算法,即带有精英保留策略的快速非支配多目标优化算法,是一种基于Pareto最优解的多目标优化算法。本节介绍了通过预先设定带有偏好的参考点和利用内存保留最优解的方法改进的NSGA-II算法。
2.1 NSGA-II算法
2000年DEB等[10]提出第2代非支配排序遗传算法(NSGA-II)。该算法采用快速非支配排序降低计算复杂度,利用拥挤度及比较算子代替共享半径,引入精英策略扩大采样空间,提高了鲁棒性和运算速度。文献[11]提出了一种基于参考点的NSGA-III算法,该算法遵循NSGA-II框架,将若干均匀分布的理想点设为参考点。通过提供和自适应更新一些分布良好的参考点替换拥挤距离算子,来维持种群成员之间的多样性。在解决3个目标以上的多目标优化问题中取得了很好的效果[12]。文献[13]针对动态环境下的多目标进化问题设计了新的动态和迁移策略,提高了算法收敛速度,但复杂度依然较大。
2.2 预设参考点
假设每个天线向周围均匀监测辐射源信号且最大监测半径R相同。通过计算障碍物之间的距离s,并比较s与R的大小来预先设定带有偏好的参考点作为天线的部署位置,流程如图3所示。
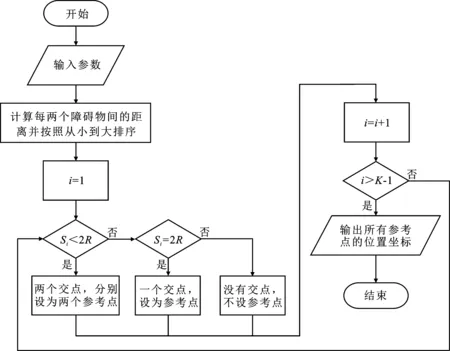
图3 预设参考点流程图
首先,输入监测区域ROI的范围,即天线数量M和监测覆盖范围最大半径R,障碍物数量K和位置坐标,天线间保持通信的最大距离lmax;然后,计算每两个障碍物之间的距离s,并按照从小到大的顺序排序,判断si与2R的关系,进而确定参考点数量和位置坐标。
在保证覆盖率的前提下,障碍物在天线覆盖范围边缘时对其正常工作的影响最小。如图4所示,实心三角形为障碍物,实心圆形为参考点,天线监测覆盖范围(实心圆)最大半径为R,两个障碍物之间的距离为s,虚线圆是以障碍物为圆心、R为半径的圆。
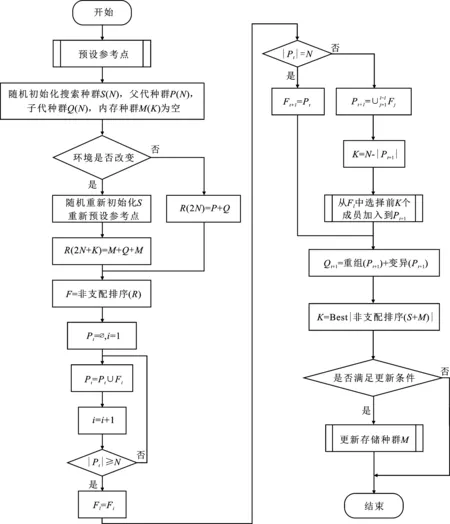
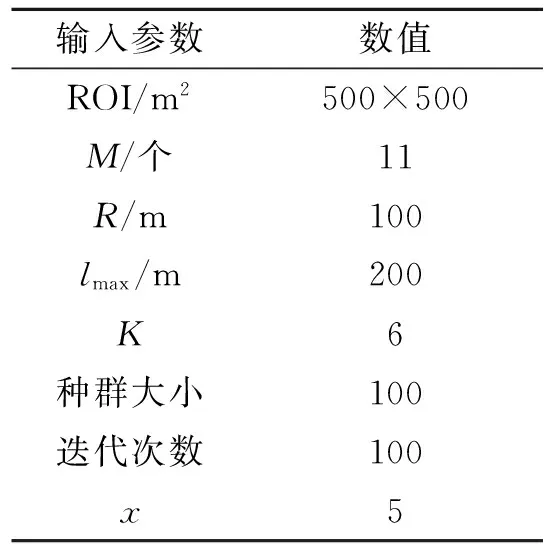
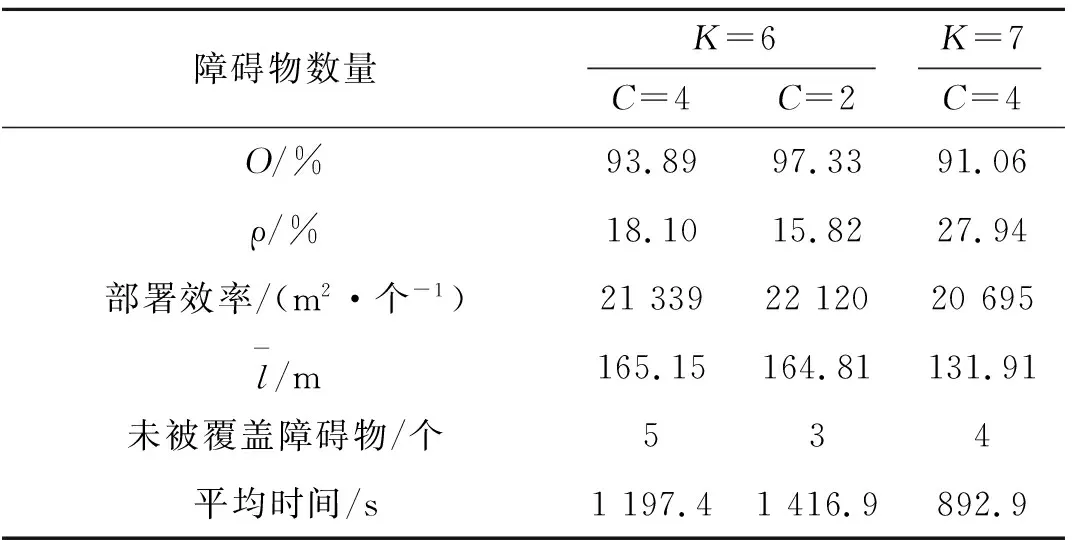
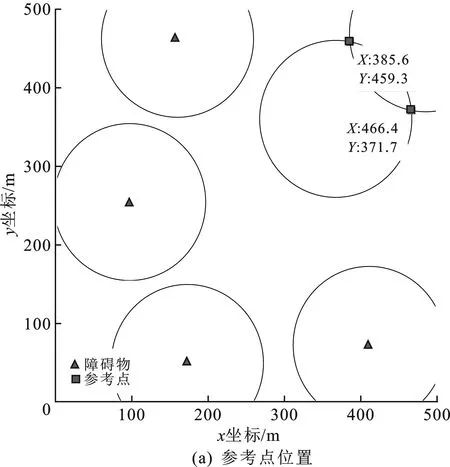
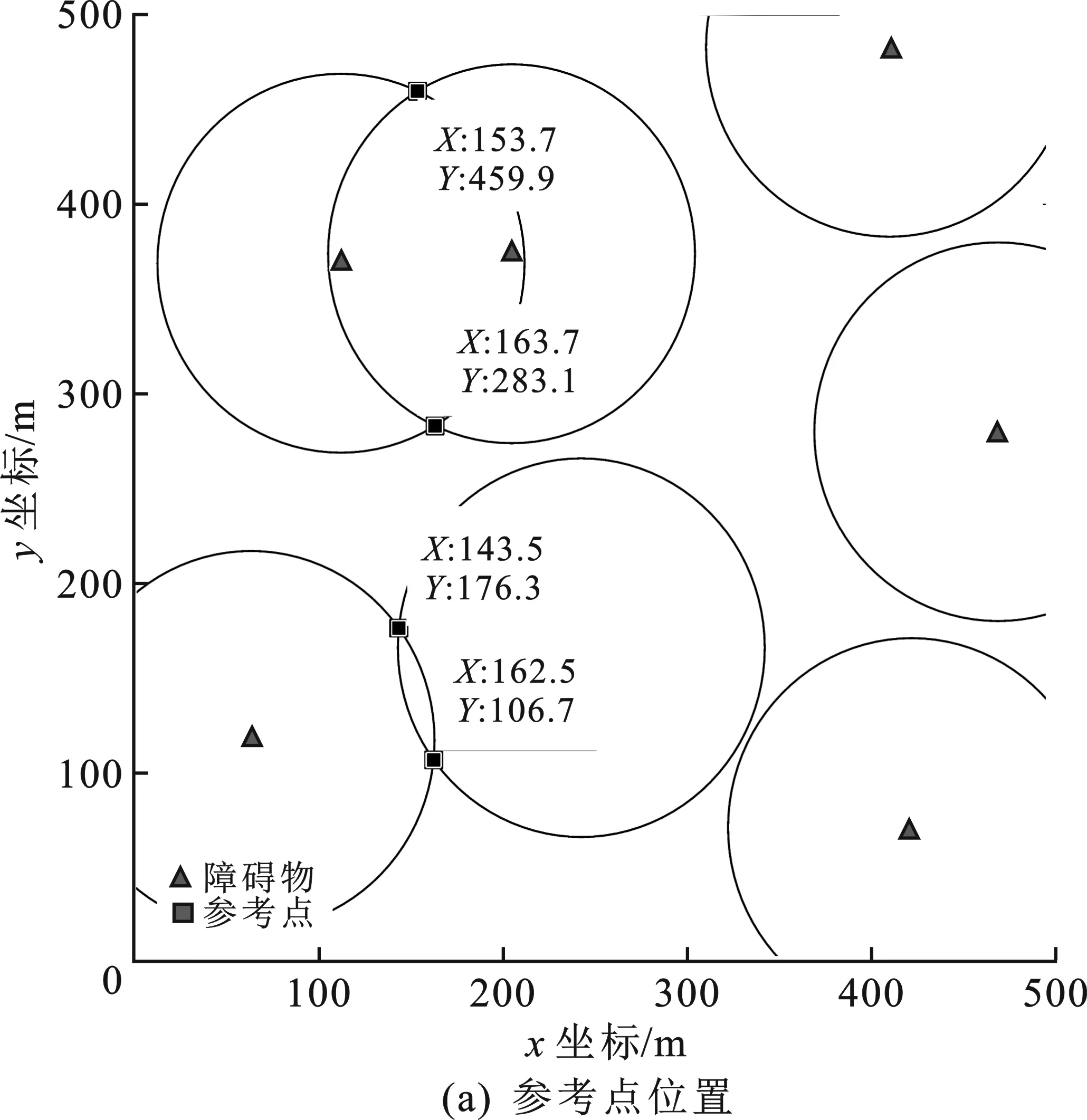
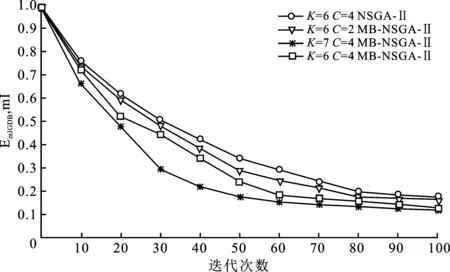
当0 图4 不同情况下参考点位置 当s=2R时,如图4(b)所示,虚线圆有一个交点,设为参考点,两个障碍物都位于天线覆盖范围边缘上,对监测范围内的准确监测影响最小。如果参考点设在障碍物1的虚线圆的其它位置上,那么在部署第2个天线使障碍物2位于其覆盖范围边缘时,会导致覆盖率减小和冗余率增大,并且需要部署两个天线才能避免两个障碍物的影响,增加成本;如果保证最大覆盖率和最小冗余率时,将导致障碍物2位于该天线监测覆盖范围内,监测准确性变差。 当s>2R时,虚线圆没有交点,虚线圆上任意位置都可以设为参考点。如图4(c)所示,如果s<4R,则选取参考点位置时要避免覆盖冗余,两个实心圆相切时部署效率最高。如果s≥4R,则参考点位置没有限制,如图4(d)所示。 为了增强NSGA-II算法在动态环境下跟踪非支配解的能力,在算法中使用显式内存来存储每一代的最佳解。每当发生环境改变时,搜索种群将随机重新初始化并为存储种群提供最优解;主种群从存储种群中得到非支配个体并对其更新。 在基于内存存储的NSGA-II算法中,存储种群的更新过程非常重要,它直接影响算法的性能。更新存储种群的流程如图5所示。存储种群的种群大小为K,索引j初始值为1。获取当前父代种群P(N),并对其非支配排序。当内存不满时,非支配解FP(j)直接添加到存储种群中。当内存满后,根据拥挤距离的概念[10]求解最小欧氏距离,得到每个非支配个体到存储种群的最近解。如果新的非支配解比它的最近解更优,则替换这两个解;否则,存储种群保持不变。 图5 更新存储种群 加入预设参考点和更新存储种群子流程后的改进NSGA-II算法(MB-NSGA-II)得到下一代种群Pt+1的流程如图6所示。程序运行前首先预设参考点,随机初始化搜索种群S、父种群P和子种群Q,种群大小为N。存储种群M大小为空。在达到迭代次数前的每一代种群中,算法都会检查环境是否发生了变化。如果环境没有变化,合并种群P和Q得到种群大小为2N的种群R。如果发生变化,重新预设参考点并随机初始化搜索种群,合并种群P、Q和存储种群M,得到大小为2N+K的种群R。 图6 主程序流程图 经过非支配排序的种群R从F1开始,逐次将各非支配层(F1,F2,…)的解添加到种群Pt中,直至Pt的种群大小首次等于N或大于N。假设在最后添加的非支配层是Fl,如果Pt的种群大小正好为N,则直接输出Pt+1=Pt;否则首先将前Fl-1个支配层的所有解添加到种群Pt+1,然后利用小生境算法[14]选取Fl中的前K个解添加到Pt+1中,得到大小为N的Pt+1。Pt+1经过重组和变异得到种群Qt+1。对合并后的搜索种群S和存储种群M非支配排序,得到合并种群的最优非支配解的个数K,作为种群M的种群大小。在满足更新条件时更新种群M。将该条件设定为迭代次数x,即每迭代x次则更新一次种群M。 实验所用计算机型号为HP Z800 Workstation。处理器为Intel(R)Xeon(R)CPU X5675@3.07 GHz(2处理器),安装内存(RAM)为12.0 GB;仿真软件为MATLAB 2016a版本。需要输入的参数及其数值如表1所示。 表1 输入参数 6个障碍物坐标分别为(172,50)、(159,463)、(367,361)、(244,200)、(411,73)、(485,470)。得到参考点和天线部署位置如图7所示,部署结果数据如表2所示。 表2 部署结果数据 图7(a)中4个参考点坐标分别为(158,149)、(258,101)、(385.6,459.3)和(466.4,371.7),其中,K为障碍物数量,C为参考点数量。图7(b)中18条直线段表示天线间的通信链路,平均通信距离为165.15 m,覆盖率为93.89%,冗余率为18.10%。部署效率表示平均每个天线有效监测覆盖范围为21 339 m2,平均迭代一次的时间为1 297.9 s,有5个障碍物完全不在天线覆盖区域内。 将障碍物4的坐标改为(96,255),得到参考点和天线部署位置如图8所示,部署结果数据如表2所示。其中,两个参考点坐标分别为(385.6,459.3)和(466.4,371.7),共有18条通信链路,平均通信距离为164.81 m。未被覆盖障碍物数量3/0个表示有3个障碍物完全未被覆盖:障碍物1位于天线4和10的覆盖范围边缘交点处,障碍物3位于天线1、2和7的覆盖范围边缘交点处;障碍物6位于天线1和2的覆盖范围边缘交点处。 图8 K=6,C=2时参考点和天线部署位置 参考点数量C=2时的算法平均迭代一次的时间是C=4时的1.18倍,原因是在部署优化过程中,天线位置是决策变量,在天线数量一定的情况下,预设的作为天线位置的参考点越少,则作为决策变量的未知部署位置的天线数量的个数越多,所以求解时间更长。 当算法迭代60次时随机改变障碍物数量和位置:7个障碍物坐标分别为(63,117)、(112,369)、(423,71)、(205,374)、(411,483)、(243,166)和(470,280),得到参考点和天线部署位置如图9所示。4个参考点坐标分别为(153.7,459.9)、(163.3,283.1)、(143.5,176.3)、(182.5,106.7),共有21条通信链路,平均通信距离为131.91m。部署结果数据如表2所示,平均迭代一次的时间比K=6时降低了25.43%。这是因为决策变量始终是除了4个参考点外余下的7个天线的部署位置,改进算法MB-NSGA-II中利用存储种群存储K=6时的非支配个体,在改变环境后重新部署天线位置时从存储种群中选取最优个体可以更快地找到Pareto解。 图9 K=7,C=4时参考点和天线部署位置 由表2可知,在部署天线数量一定的情况下,障碍物数量相同时,参考点数量越多,则覆盖率越小,冗余率越大,平均迭代一次的时间越短。这是因为参考点作为天线部署位置在寻求最优解前已经确定了坐标,导致部署其它天线时不可避免地造成冗余率的增加和覆盖率的减少;但同时参考点数量越多,则未确定位置的天线数量越少,求解速度更快。参考点数量相同时,障碍物数量越多,则覆盖率越小,冗余率越大。K=7时的冗余率是K=6时的1.54倍,说明以未被覆盖障碍物数量作为优化多目标之一时,障碍物的数量对冗余率的影响很大。 算法评价指标(the mean Inverted Generational Distance just Before the change,mIGDB)量EmIGDB可以用来计算发生下次变化前平均反转世代距离[15]。该指标量EmIGDB计算代价小,可同时评价算法收敛性和多样性。EmIGDB值越小,说明算法综合性能越好。该指标计算方法为 (10) 其中,EIGDt为只计算下次改变前的反转世代距离,n为变化次数。 当没有发生环境变化时,利用(the mean Inverted Generational Distance,mIGD)量EmIGD评价算法的收敛性和多样性。该指标EmIGD计算方法为 (11) 其中,Gn是迭代次数,EIGDt为反转世代距离。 依托多目标优化平台PlatEMO[16],在不同障碍物和参考点数量的情况下运行MB-NSGA-II或NSGA-II算法,得到EmIGD(或EmIGDB)指标量随迭代次数变化的结果如图10所示。当收敛条件为EmIGDB=0.2时,4种情况下算法收敛时的迭代次数X和平均迭代一次的时间t如表3所示。当K=7,C=4时,从存储种群中选取最优个体,收敛速度最快且平均迭代一次的时间最短,3种方法都比NSGA-II算法收敛速度更快,说明应用预设参考点的方法可以有效减少迭代次数和时间。 图10 不同条件下的EmIGD指标量随迭代次数的变化情况 表3 算法性能比较 在部署天线数量和障碍物数量一定时,参考点数量越多,算法收敛的越快,平均迭代一次的时间越短;应用MB-NSGA-II算法可以有效减少算法收敛的迭代次数和迭代时间。 障碍物对地面天线监测电磁辐射源信号的准确性带来不利影响,笔者针对此问题构建了以覆盖率、冗余率、未被覆盖障碍物数量为目标的多目标优化模型。通过判断障碍物间距离与天线监测覆盖范围最大半径的大小关系来预先设定参考点作为若干天线的部署位置。通过仿真验证了以增加冗余率为代价可以有效减少天线覆盖范围内的障碍物数量:K=6时,5个障碍物都未被覆盖;K=7时,4个障碍物未被覆盖。比较了不同参考点数量对冗余率和收敛时迭代次数等部署结果的影响。预设的参考点越多,收敛速度越快,但冗余率也会增加。利用存储种群存储前几代非支配解的方法改进NSGA-II算法,在改变障碍物数量和位置后,可以快速找到新的最优解,求解速度是原来的74.57%。通过mIGDB算法评价指标验证了改进算法MB-NSGA-II相比于NSGA-II算法可以提高部署效率和算法收敛速度。 下一步工作将针对算法检测环境变化的实时性和优化存储种群的更新策略进行深入研究。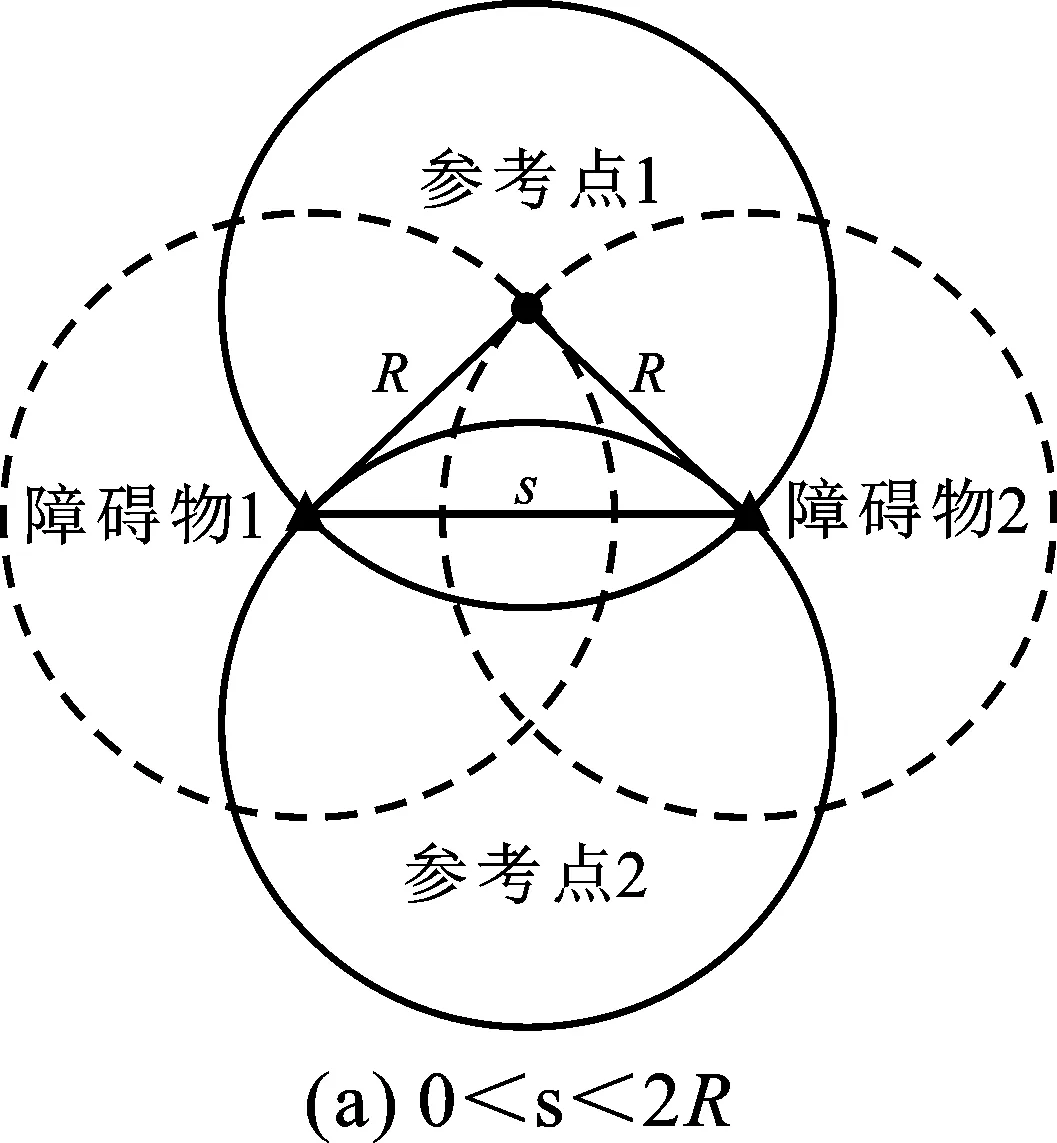
2.3 更新存储种群

2.4 算法流程
3 实验仿真及分析

4 结束语
