一种利用量测空间聚类的多帧检测前跟踪算法

张佳琦，陶海红，张修社，韩春雷

(1.西安电子科技大学 雷达信号处理国家重点实验室，陕西 西安 710071；2.西安导航技术研究所，陕西 西安 710068)

多目标跟踪[1]是目标跟踪领域的研究热点，经过几十年的发展获取了大量的研究成果[2-4]。传统的多目标跟踪方法[5]利用门限检测后的点迹进行目标轨迹估计，门限检测的目的是滤除大量杂波，保留真实目标点迹。然而，在低信噪比(Signal Noise Ratio，SNR)环境下，传统的多目标跟踪算法具有一定的局限性。检测前跟踪技术(Track Before Detect，TBD)[6]通过直接处理无门限或低门限点迹，并对目标的多帧量测点迹进行能量积累，能够在低信噪比环境下实现弱小目标的检测和跟踪。检测前跟踪技术经过了几十年的发展，形成了诸多流派[7-10]，其中基于动态规划的检测前跟踪算法(Dynamic Programming Track Before Detect，DP-TBD)[11-13]因其算法结构简单、易于工程实现，受到了众多学者的青睐。其中，文献[14-17]研究了机动目标的DP-TBD算法，文献[18-20]针对多目标场景的DP-TBD算法开展研究，文献[21-22]对多目标临近场景的DP-TBD算法进行研究，文献[23-24]开展了两级处理结构的DP-TBD算法研究，文献[25-26]进行了迭代框架的DP-TBD算法研究，文献[27-28]进行了多传感器的DP-TBD融合算法研究。另外，文献[29-30]针对检测场景的杂波分布和目标特性开展DP-TBD算法研究。

在实际应用中，DP-TBD算法面临最大的挑战仍然是较高的运算复杂度。在多目标场景下，文献[20-22]提出的基于连续目标撤销策略的DP-TBD算法(Succession Track Cancel Dynanic Progremming Track Before Detect，STC-DP-TBD)能够有效改善目标临近时的多目标检测和跟踪性能。然而，当场景中目标、虚警数量增加时，算法的运算复杂度将呈现几何级数增长。由于缺少目标运动先验信息，算法采用观测空间全局DP-TBD处理，导致运算复杂度高的问题，笔者提出一种利用量测空间聚类的DP-TBD算法(Measurement Space Clustering Dynamic Programming Track Before Detect，MSC-DP-TBD)。该算法构建在文献[23-24]提出的两级处理框架之上，利用跨多帧策略构建状态转移集合，并依据状态转移集合对量测点迹进行标签构建，获取点迹在量测空间上的分布信息，形成量测点迹的空间聚类，在各聚类的子空间内独立的运行STC-DP-TBD算法。通过仿真实验可知，该算法与STC-DP-TBD算法检测性能相当，但运算复杂度大幅降低。

1 问题描述

传统的DP-TBD算法通过对状态空间进行离散化，构建航迹的状态转移集合对离散空间进行遍历，通过积累航迹的多帧量测点迹的能量，实现弱小目标检测。该处理方式需要对离散空间中可能存在的所有目标进行遍历，算法的运算复杂度随着观测空间和积累帧数的增加呈几何级数增长。针对算法运算复杂度高的问题，文献[21]提出了一种两级处理的DP-TBD算法(Two Stage Dynamic Programming Track Before Detect，TS-DP-TBD)，处理结构如图1所示。

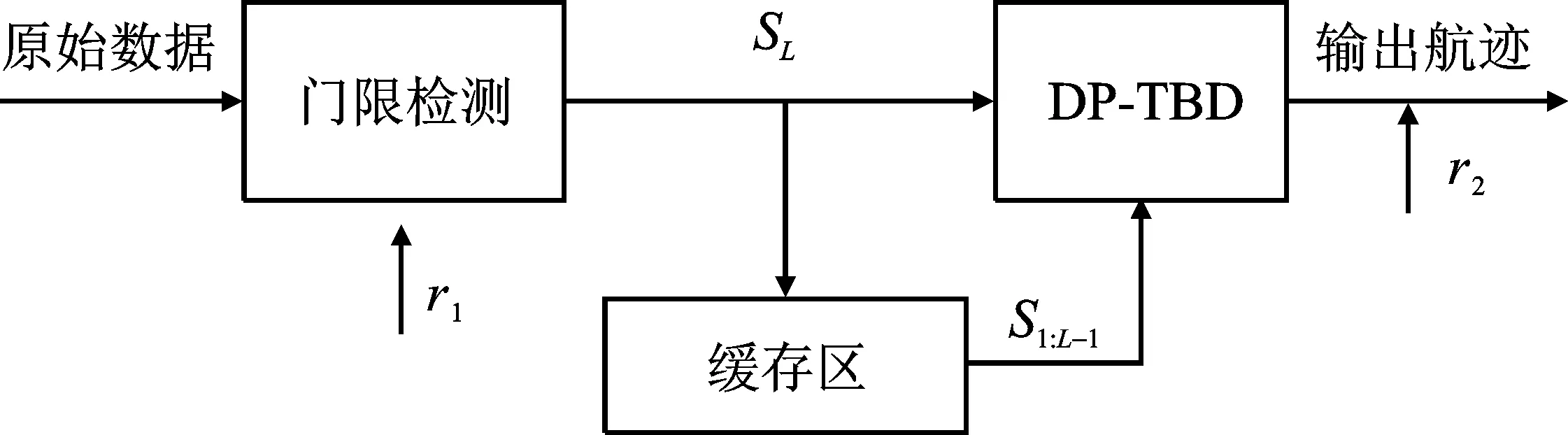
图1 TS-DP-TBD 处理结构

该处理结构与传统结构相比，可以利用一级检测门限滤除虚警似然点迹，保留目标似然点迹，减少无效的点迹状态转移关联关系运算，能够大幅度降低算法的运算复杂度。TS-DP-TBD算法在多目标情况下，尤其是目标位置邻近时，强幅度目标容易遮挡弱目标，导致弱目标难以检测。针对上述问题，文献[22]提出了STC-DP-TBD算法。该算法在航迹构建过程中采用连续航迹撤销策略，将确认航迹包含的点迹进行剔除处理，降低确认航迹对潜在航迹构建的干扰，并在文献[31]中利用雷达真实量测数据对该算法的有效性进行了验证。然而，STC-DP-TBD算法在对多目标进行检测时，由于缺少目标运动的先验信息，需要在全域量测空间内进行航迹遍历，随着场景中目标、虚警数量的增加，运算复杂度大幅提升。

2 量测空间聚类

如图2(a)所示的多目标场景，场景中目标运动轨迹存在“交叉”“平行”等邻近状态，相互邻近的目标在航迹构建时存在“共享”的量测点迹。利用“共享”的量测点迹构建起航迹之间的关联关系，依据这种关系可以对量测空间的点迹进行聚类划分，在空间上形成多个相互解耦的聚类，如图2(b)所示。基于以上思想，笔者提出利用根标签聚类的量测空间聚类划分方法，详细过程如下。

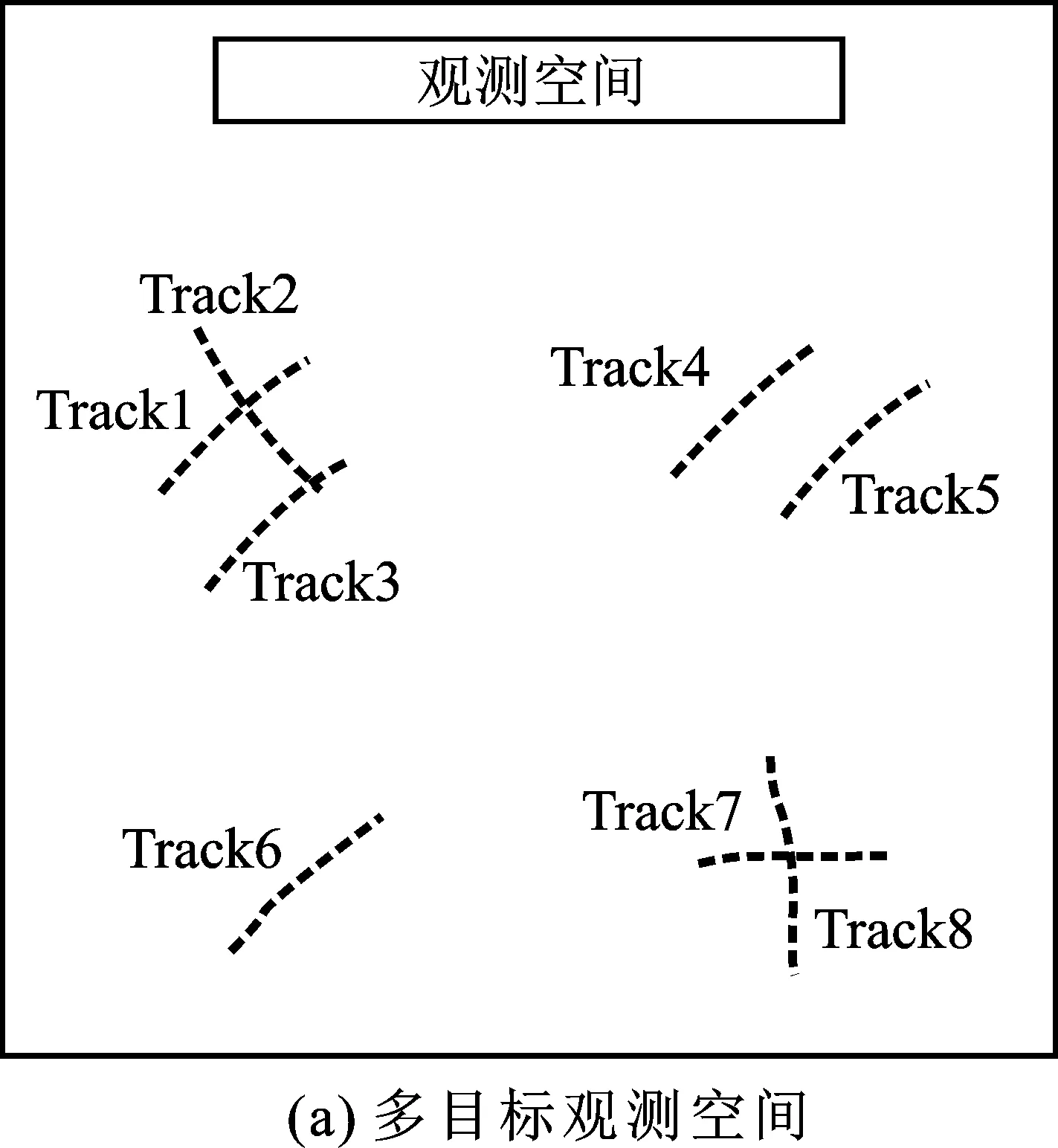
图2 多目标观测空间及聚类划分

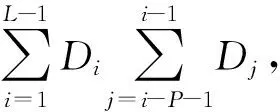
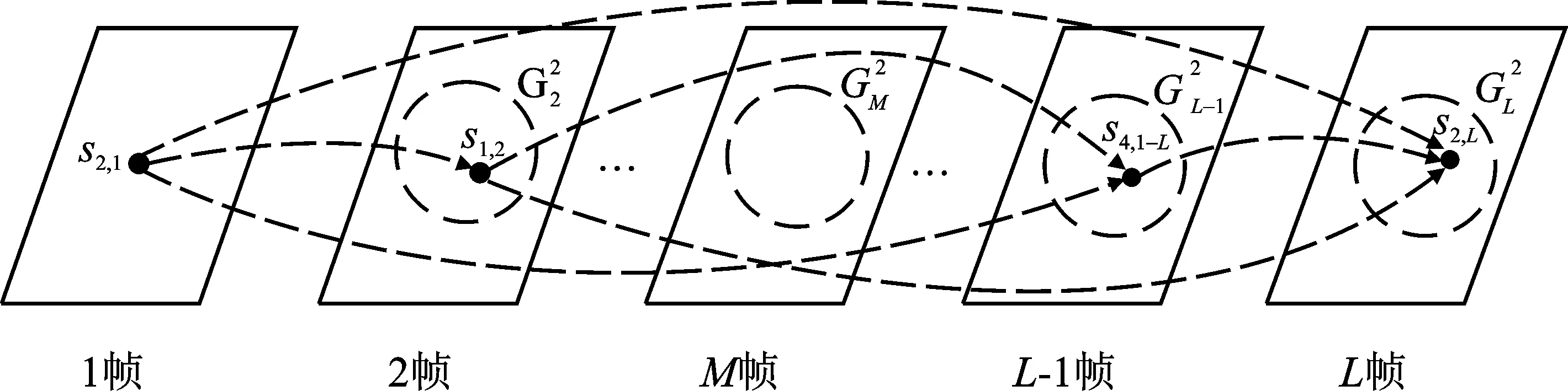
图3 跨帧状态转移集合构建

构建出的状态转移集合M可表示为

(1)

利用构建的状态转移集合对量测空间的点迹进行根标签标记，标记过程如图4所示。对第一帧中包含的量测点迹标记为根标签，依据状态转移集合依次对第2至第L帧量测点迹进行根标签标记。利用根标签的传递性和继承性，在第L帧量测点迹的根标签集合中能够获取根标签的连通性信息。

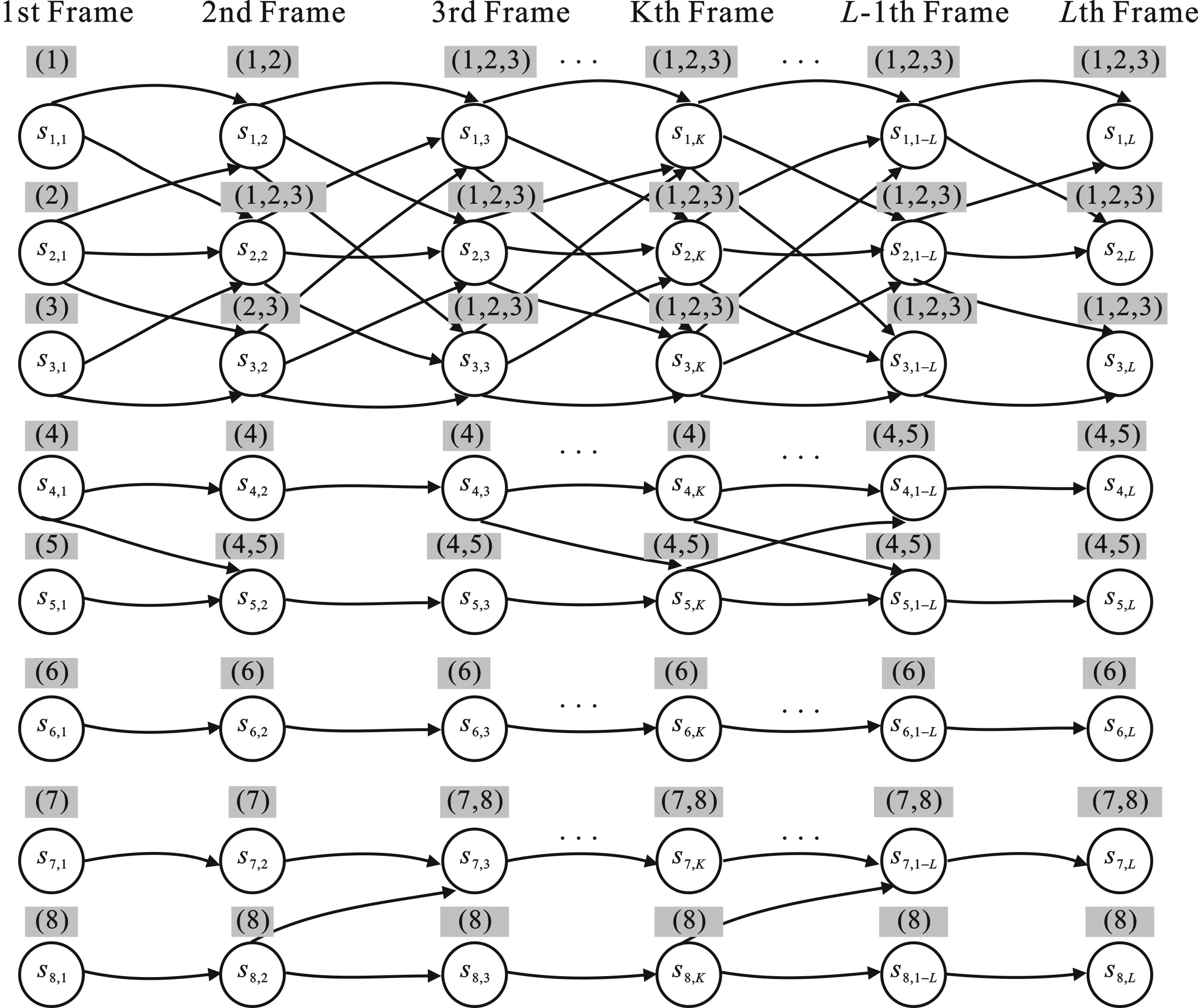
图4 标签标记

依据第L帧量测点迹的根标签信息进行根标签连通性判断，相互连通的根标签划分为同一个聚类，则有

(2)

(3)

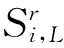
(4)

其中，|C(i)|表示量测空间聚类个数，|C(i，j)|表示第i个聚类中的第j个目标的所有量测点迹。

3 算法描述

针对STC-DP-TBD算法运算复杂度高的问题，提出了MSC-DP-TBD算法。该算法采用跨多帧构建关联集合，依据状态转移集合对量测点迹进行根标签标记，通过根标签联通性计算形成量测点迹的空间聚类划分，并在各聚类内采用STC-DP-TBD处理，可有效降低算法的运算复杂度。算法步骤如图5所示。

图5 MSC-DP-TBD处理结构

3.1 算法处理步骤

3.1.1 量测空间聚类

利用最大速度约束在不同帧的点迹之间计算状态转移关系，构建出多帧量测点迹的状态转移集合。依据状态转移集合对量测空间中的点迹进行标记并形成空间聚类，生成的不同聚类之间的量测点迹不相交。聚类之间的点迹关系如下：

C(i)∩C(j)=∅，i，j=1，2，…，N，

(5)

(6)

3.1.2 航迹构建

在各聚类内独立的执行基于STC策略的航迹构建算法，通过积累量测点迹的幅度信息计算出临时航迹的得分函数F()及可回溯状态τ()：

(7)

(8)

其中，z表示航迹中关联点迹的幅度信息。

3.1.3 航迹确认

利用二级检测门限γ2和构建的航迹的得分函数进行对比，对构建航迹进行确认或删除，

(9)

3.1.4 航迹平滑

通过对确认航迹的量测点迹序列进行平滑处理，获得更高跟踪精度的航迹状态。

3.2 运算复杂度分析

STC-DP-TBD算法的运算复杂度主要集中在计算状态转移集合和构建航迹两个步骤，计算状态转移集合平均时间复杂度约为O(PL[(NrNθ-K)FFAR+KPd]2)，其中，P为航迹允许缺失最大点迹数量，L为积累的量测数据帧数，Nr和Nθ分别为距离和方位角的分辨单元数量，K∈{1，…，NrNθ}为场景中的目标数量，FFAR为虚警率，Pd为检测概率。假定航迹构建步骤的时间复杂度为O(TFstc)，则STC-DP-TBD算法的运算复杂度约为

O(STC-DP-TBD)≈O(PL[(NrNθ-K)FFAR+KPd]2)+O(TFstc) 。

(10)

假定MSC-DP-TBD算法的聚类个数为N，航迹构建算法的时间复杂度为O(TFmsc)，则有如下关系：

O(TFstc)/N≤O(TFmsc)≤(TFstc) 。

(11)

则MSC-DP-TBD算法的运算复杂度约为

O(MSC-DP-TBD)≈O(PL[(NrNθ-K)FFAR+KPd]2)+O(TFmsc) 。

(12)

因此，有

O(MSC-DP-TBD)≤O(STC-DP-TBD) 。

(13)

当聚类个数N增加时，MSC-DP-TBD算法的运算复杂度会得到明显改善。

表1给出了两种算法运算复杂度的对比。

表1 运算复杂度对比表

4 数值分析

为了评价TS-DP-TBD、STC-DP-TBD及MSC-DP-TBD等算法的检测性能，特采用的评估指标如下：

(1)有效检测航迹数(Nvd)，即真实航迹被检测到的数量；

(2)虚假检测航迹数(Nfd)，即检测到的非真实航迹的数量；

(3)漏检航迹数(Nld)，即真实航迹未被检测到的数量。

仿真场景设置如图6所示。场景构建了X-Y两维平面空间，空间尺度大小为14 km×14 km，包含12批匀速运动目标，在空间上可简单地划分为5个聚类，目标1和目标2、目标7和目标8为两组平行运动，目标3和目标4、目标5和目标6为两组交叉运动，目标9、目标10、目标11及目标12为相互临近运动，目标的运动方向如图6的箭头所示。算法多帧积累的帧数L=10，跨帧构建状态转移集合的最大丢点个数P=3，输出航迹有效长度Q=5，连续帧构建状态转移集合的航迹外推点数R=3，最大加速度Vmax=600 m/s。1级检测门限γ1依据FFAR确定，2级检测门限γ2由105次蒙特卡罗仿真实验确定。

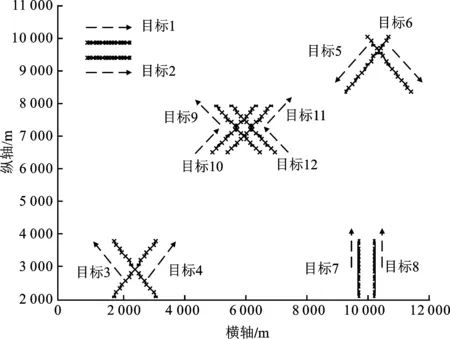
图6 仿真场景设置

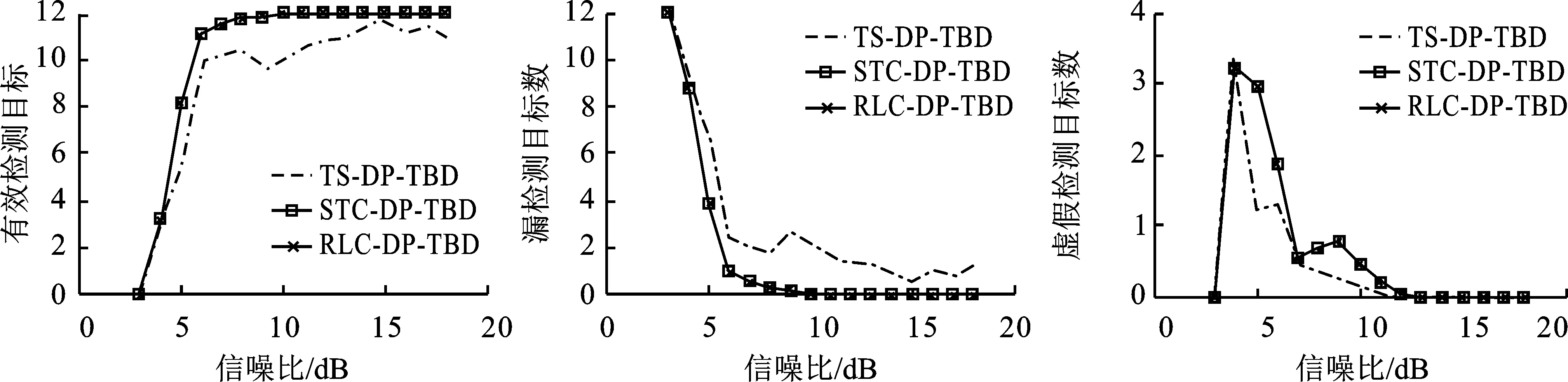
图7为FFAR=10-1时，3种算法在不同信噪比下的检测性能对比，图7(a)～(c)分别为有效检测目标数、漏检目标数及虚假检测目标数的对比曲线。由图7(a)和(b)可知，TS-DP-TBD算法的检测性能最差，原因是该算法采用航迹剪枝机制，在目标临近时难以检测弱回波目标。STC-DP-TBD、MSC-DP-TBD两种算法的检测性能相当，原因是上述两种算法均采用STC处理策略，能够对临近目标进行有效检测。由图7(c)可知信噪比小于等于7 dB时，3种算法采用跨多帧构建状态转移集合，在状态转移集合的构建过程中，关联波门逐步扩大，导致虚假航迹在运动空间进行积累，产生大量的虚假航迹；当信噪比大于7 dB时，以上算法几乎不存在虚假航迹，原因是在高SNR下通过得分函数的能量积累能够有效区分真实航迹和虚假航迹。

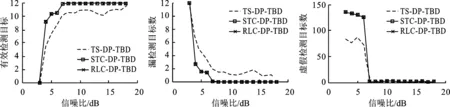
(a)有效检测目标数 (b)漏检测目标数 (c)虚假检测目标数

图8、图9分别为FFAR=10-2、Pfa=10-3时，3种算法在不同信噪比下的检测性能对比，由图8以及图9(a)和(b)可知，在信噪比小于等于7 dB时以上算法均存在不同程度的漏检，原因是在低FFAR下一级检测门限升高会剔除部分目标真实点迹导致漏检，而当SNR>7dB时，仅TS-DP-TBD算法存在漏检，另外两种算法均不存在漏检且检测性能相当。由图8和图9(c)可知，在低FFAR下以上算法仅存在较少数量的虚假航迹，原因是在低Pfa下一级检测门限升高会剔除绝大部分虚假点迹，抑制虚假航迹的产生。

(a)有效检测目标数 (b)漏检测目标数 (c)虚假检测目标数

(a)有效检测目标数 (b)漏检测目标数 (c)虚假检测目标数

由表2可知，在不同FFAR下MSC-DP-TBD相较STC-DP-TBD算法在运算效率上均有明显提升。该算法采用根节点标签对量测数据进行空间聚类划分，在不同聚类之间进行解耦的独立处理，可有效剔除无效点迹对航迹构建的关联干扰。另外，由STC-DP-TBD与MSC-DP-TBD两种算法在不同Pfa下的运算复杂度对比可知，聚类步骤最多能够降低算法50%以上的运算复杂度。

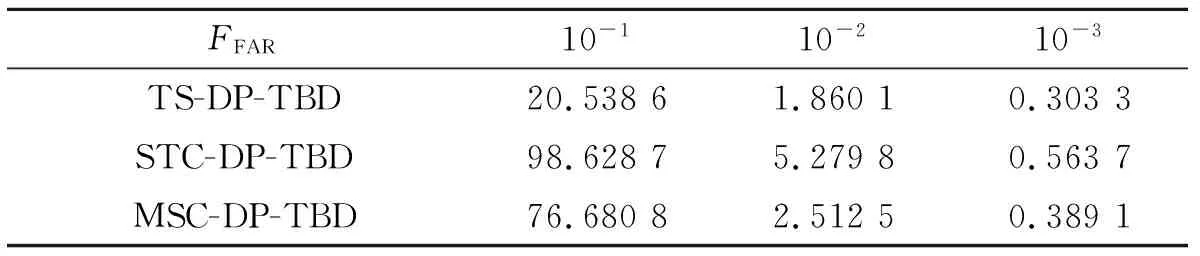
表2 执行时间对比表 s

5 结束语

笔者分析了TS-DP-TBD算法和STC-DP-TBD算法的特点和不足，针对TS-DP-TBD算法在多目标邻近时检测性能下降，STC-DP-TBD算法的运算复杂度高，工程上难以实现，提出了一种对量测空间进行聚类的MSC-DP-TBD算法。该算法通过构建状态转移集合并对量测点迹进行标签标记，获取多目标在量测空间的分布特征，通过聚类处理对量测空间进行划分，并在不同聚类内独立运行STC-DP-TBD算法。通过数学分析与仿真实验可知，所提算法的检测性能与STC-DP-TBD相当，同时运算复杂度大幅度降低。仿真实验和性能分析验证了该算法的有效性和工程的可行性。