深度非对称压缩型哈希算法

闫 佳，曹玉东，任佳兴，陈冬昊，李晓会

(辽宁工业大学 电子与信息工程学院，辽宁 锦州 121001)

随着互联网产业，通信行业，以及智能终端硬件的发展，互联网上的图像及视频数据量大量增加。海量数据的拥有者面对大规模数据的检索需求，传统图像检索算法面临着巨大的挑战。基于哈希的图像检索算法解决了传统检索方法会引起的维数灾难问题，逐渐受到研究人员的重视。深度哈希的方法通过深度卷积网络拟合哈希函数，能完成从图像特征到二进制哈希码的映射，生成的二值码通过匹配汉明距离完成图像搜索。但如何有效地获取复杂背景下的目标图像的语义相关性，将其映射为相同或相近的哈希码，提高图像的检索精度，仍是一个具有挑战性的问题。

深度哈希网络可以从输入图像中自动地学习到高维特征表示，然后映射为紧凑的二进制哈希码，需要的存储空间较少，这种方式生成的哈希码能够解决实值特征低效的问题[1]，并将数据的相似关系转化为汉明距离通过快速的异或运算来度量[2]。映射后的哈希码也能够保留原有语义特征在图像中的分布特性，且能够极大地减少图像检索所需要的时间和内存，基于哈希的检索方法适合大规模图像检索[3]。

现有的大多数深度哈希的方法，对查询集图像及数据库集图像会学习同一个哈希映射函数。这种对称结构的哈希学习方法需要考虑成对样本之间的相似性，所以会消耗大量训练时间。假设当训练样本数量为n时，需要考虑n2对样本的相似性，当数据库很大时，会导致训练时间过长。为了加快模型的训练过程，大多数深度哈希算法会从数据库中抽取一个小的子集去训练深度卷积网络，以减少计算成本。文献[4]提出的CNNH(Convolution Neural Network Hashing)算法将深度学习与哈希模型结合，把图像特征学习和哈希函数优化融合到一个框架内，使用平方损失函数输出最终的哈希值，图像检索效果得到了显著的提升。文献[5]将成对的图像(相似/不相似)用于损失函数构造中，使得模型学习到的哈希二值码更加紧凑。文献[6]提出DFH算法，为深度监督哈希算法设计了费舍尔损失函数，再次提高了从图像到哈希码的映射准确度。但对称结构的深度哈希算法，训练过程中的绝大多数的数据点并未一次性包含在损失函数计算中，因此这些方法很难有效利用大规模数据库的监督信息，导致搜索性能不佳。为了解决这一问题，文献[7]提出了非对称结构的哈希方法，利用两个深度卷积网络分别学习数据库集和查询集图像，相当于映射了两种不同的哈希函数，构建了非对称的学习方法，但监督信息没有直接用于离散编码过程。文献[8]通过使用非对称优化的方式训练模型，但优化过程中无法得到用于深度网络的学习的数据库最优哈希值。不同于文献[7]构建的两种不同的哈希映射函数，文献[9]使用一个深度卷积网络，利用查询集图像构建深度哈希函数，并且直接将监督信息用于编码过程，然后通过离散优化得到最优的哈希码，但是该模型未对生成哈希码的紧致性与分离性进行约束，导致处于同类边缘的困难样本难以有效地训练。

针对上述方法的不足，笔者提出了一种非对称压缩型深度哈希算法(Asymmetric Compression Deep Hashing algorithm，ACDH)，可以在使用一个神经网络的情况下完成不对称深度哈希模型的训练，使深度哈希网络学习到紧凑的哈希码。该方法主要贡献如下：① 提出了一种端到端的深度哈希模型，使用不对称的方式训练模型，将监督信息直接作用于离散编码过程，使数据库全局监督信息得到有效的利用；② 设计一种融合大规模监督信息和相似度信息的损失函数，并在训练深度哈希网络时对生成的哈希码进行显式约束，使生成的同类图像哈希码的紧致性与不同类哈希码的分离性可以被调控，提升了哈希码对困难样本的判别能力；③ 大量实验结果表明所提算法相较于其他主流深度哈希方法，在性能上有显著提升。

1 非对称压缩型深度哈希算法

笔者提出的算法流程框架如图1所示，包括深度卷积网络和二值码优化两部分，这两部分交替优化同一个目标损失函数。图1中实线箭头是深度卷积网络训练时数据流动方向，虚线箭头是二值码优化部分的数据流动方向。训练深度卷积网络时，二值优化部分的参数和虚线箭头的数据流动会被固定；同样，进行二值码优化时，深度卷积网络的参数和实线箭头的数据流动会被固定。深度卷积网络仅用于学习查询集图像的哈希码U，输出的查询集经过交替方向乘子算法(Alternating Direction Method of Multipliers，ADMM)优化算法[10]求解得到最优的数据库集哈希码V，V被用于下一次深度卷积网络的学习，这样可以在仅使用一个深度卷积网络的情况下完成不对称深度哈希的迭代学习过程。

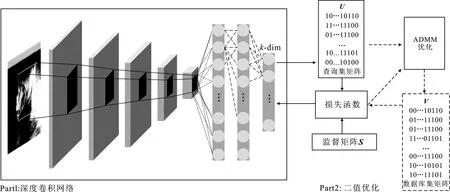
图1 ACDH模型结构

1.1 公式符号定义

(1)

1.2 深度哈希网络

图2 SKNet模块结构

将上述SKNet模块嵌入到ResNet-50中，再添加一个哈希层和阈值化层，用于输出二值哈希码。新的特征提取网络增加了更多的非线性，可以更好地拟合通道间复杂的相关性。其参数设置如表1所示。

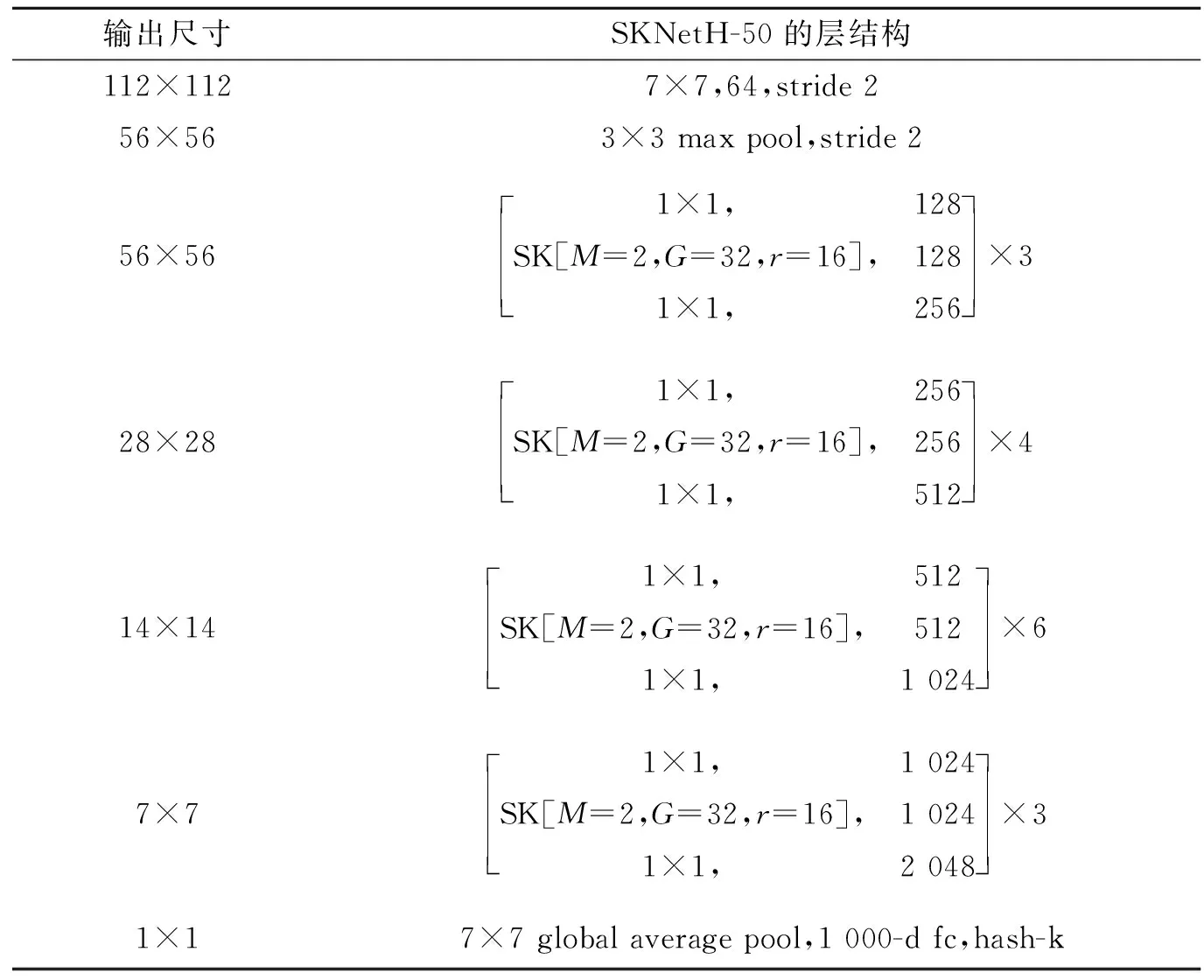
表1 改进的SKNet-50的网络结构

1.3 损失函数

文献[5]通过使用合页函数构建了一个相似性损失函数。该方法采用对称的方式训练网络，数据集的全局监督信息并未得到有效利用。文献[9]采用不对称的方式设计损失函数。该损失不仅用于深度神经网络的学习，也用于优化函数对数据集矩阵的学习。但此方法并未对相同类别图像与不同类哈希码之间的差异性进行有效约束。包括ADSH[9]在内的一些深度哈希方法在损失函数中仅使得同类图像的哈希码距离尽可能地小，甚至强制约束同类别图像哈希码距离为零，而对于不同类图像哈希码映射，简单地将其推远。不同于上述方法，笔者希望同类图像的哈希码之间有一个微小的距离，保留同类图像映射的哈希码之间的某种差异性，并且使不同类图像的哈希码之间的分离程度尽可能一致。笔者设计的损失函数鼓励图像映射的哈希码之间保持一个合理的距离，从而减轻在训练迭代时处于同类边缘的困难样本点对于其他类别哈希码的影响。

受文献[5]和文献[8]的启发，笔者设计了如下损失函数。设数据库集图像对应的哈希码为vj，查询集图像对应的哈希码为ui，在损失函数中激励相似图像的哈希码保持一个微小的间隔，不相似图像的哈希码之间有一个较大的距离，即满足：

(2)

其中，θ≥ε≥0，使用合页函数可以实现式(2)的约束，代入可得

(3)

其中，Sij=1时，只有当dham(ui，vj)-(θ-ε)≤0时，损失为0。Sij=0时，只有当(θ+ε)-dham(ui，vj)≤0时，损失为0。简言之，该损失函数激励了成对相似的vj和ui与成对不相似的vj和ui之间始终相差2ε。因为上述合页函数在0处不可导，文献[13]采用了h(x)=1/l×ln(1+exp(lx))来近似合页损失函数；但在实际操作中exp(lx)会有数值溢出的情况。鉴于x只能取到非零值，令

(4)

其中，l为近似函数的平滑系数。使用函数h(x)近似式(3)中的合页函数max(x，0)，可得

(5)

将上述约束重写为深度哈希网络的最小化损失函数minJ(Θ，V)，得

(6)

其中，ui表示神经网络直接学习到的查询集哈希码，可以用tanh(F(xi；Θ))来替换，F(xi；Θ)表示深度神经网络的输出，Θ表示深度网络的参数集合，minJ(Θ，V)等价于：

(7)

其中，Γ={1，2，…，n}，表示所有数据库点的索引，使用Ω={i1，i2，…，im}⊆Γ来表示查询集的索引，因为Ω⊆Γ，且i∈Ω，在原有损失函数的基础上添加了一个惩罚项，使得相同索引下的数据库哈希码vi与tanh(F(xi；Θ)尽可能地接近，最终的损失函数为

(8)

上述损失函数使得哈希码之间的距离调节变得可控。通过调节θ与ε的差值大小，可以控制同类图像的哈希码之间的紧凑程度；ε控制不同类图像哈希码之间的分离程度。

1.4 优化学习

使用交替优化策略来优化深度哈希模型的参数Θ和式(8)中的V，在每次完整的迭代中，其中一个参数固定，另一个参数会被更新，这一过程会被迭代很多次。

1.4.1 固定V而优化Θ

固定参数V，定义输出为zi=F(yi；Θ)，那么可以通过链式法则∂J/∂zi计算∂J/∂Θ，然后使用反向传播算法(Back Propagation，BP)算法去更新Θ，达到优化神经网络参数的目的。

1.4.2 固定Θ而优化V

固定参数Θ，针对损失函数minJ(V)中的离散变量V进行优化，使得深度哈希模型的学习得以朝正确的方向进行。式(8)中的损失函数在优化时可以重写为

(9)

其中，φij=0.5(c-uiTvj)，Hij=σ(l[φij-(θ-ε)])，Bij=σ(l[(θ+ε)-φij])，σ(·)为sigmoid函数，const为与变量无关的常量。同时minJ(V)满足如下约束：

(10)

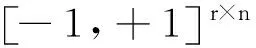
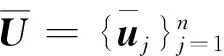
(11)

采用ADMM[10]优化式(10)，解决二值码的大规模优化问题。借鉴文献[14]的作法，使用辅助变量Z1=V且Z1∈Sp，Z2=V且Z2∈Sb来吸收约束Sp和Sb。利用ADMM优化算法需要构造如下增广拉格朗日函数：

(12)

其中，δS(·)是指示函数，当输入的Z∈S时，δS(·)为0；否则，δS(·)为∞。Y1，Y2和ρ1，ρ2表示待优化函数的对偶变量和惩罚系数。根据ADMM优化流程，通过最小化式(9)来更新原始变量V、Z1和Z2，并使用梯度上升法更新对偶变量Y1和Y2。优化3组变量的步骤如下：

更新V：在更新变量V时，固定其他变量，通过最小化下式来求得Vk+1次迭代的结果：

(13)

(14)

其中，⊙表示哈达玛乘积(Hadamard product)，即两个矩阵对应位置的元素相乘。

更新变量Z1，Z2：固定变量Vk+1和Y1，Y2可以使用近端最小化的方式更新Z1，Z2。具体形式如下：

(15)

更新Y1，Y2：使用梯度上升法更新对偶变量Y1，Y2

(16)

其中，γ是收敛系数，ADMM采用交替优化的方式逐参数更新迭代，在限定迭代次数内可完成参数V的更新，提出的ACDH算法流程如下。

算法1深度非对称压缩型哈希算法。

S∈{-1，1}m×n：监督矩阵。

c：二值码长度。

输出：

V：数据库的二值码矩阵。

Θ：神经网络的参数。

Initialization：初始化Θ，V，V初始值为全0矩阵。

foriter=1→200 do

从训练集索引Γ中随机抽取抽取Ω=2 000，X=YΩ

forepoch=1→3 do

for 1，2，…，m/Mdo

随机从X中取M个样本去构建mini-batch。

根据式(8)计算Loss，并使用反向传播算法

更新神经网络参数Θ。

end for

根据式(12)～(16)，使用ADMM优化算法更新数据库矩阵V

end for

end for

2 实验结果与分析

实验采用Pytorch-python深度学习框架与MATLAB实现，操作系统为ubuntu 20.04，显卡采用NVIDIA RTX 2 060 s，GPU显存为8 GB，运行内存为64 GB，CPU为AMD R5 3600X。

2.1 数据集

实验采用CIFAR-10[15]、NUS-WIDE[16]以及MS-COCO-2014[17]数据集。数据集划分方式和DPSH[18]与ADSH[9]一致。MS-COCO包含了82 783幅训练图片，是一种多标签的数据集，被广泛用于图像分割、分类和检索领域。在处理这一类型的数据集时，去掉了部分不包含类别信息的图片，对于包含多种类别信息的图像对，如果图像对至少有一个标签相同时，则将它们定义为相似的图像对。对于MS-COCO数据集，笔者使用修剪后的图像集作为数据集，从数据集中随机选择5 000幅图像(属于20个最大类，每个类别250幅)作为测试集，剩余图像作为训练集。CIFAR-10数据集是包含了54 000幅32×32图像的单标签数据集，每张图片都属于10个类中的一类，对于CIFAR-10数据集来说，被当作相似图像的条件是两幅图像拥有相同的标签。随机选择1 000幅图像(每个类别100幅图像)作为测试集，将剩余的图像作为训练集的数据库点。NUS-WIDE数据集，采用了从该数据集中随机选择了10 000张图像作为本实验数据集。实验中当两张图像共享一个标签时，定义为相似图像对，对于NUS-WIDE数据集，随机选择2 100张图像(每类100张图像)作为测试集，其余图像作为数据库点来训练深度哈希模型。

2.2 评价测度

使用平均精度均值(mean Average Precision，mAP)作为评价测度。在图像检索中使用前K项图像的排序情况来衡量算法的优越性，前K个检索图像的平均精度AP，可以定义为

(17)

其中，N为检索集中与查询样本相关紧邻图像的数目；P(k)表示前k个图像的检索精度；δ(k)是指示函数，当查询样本与第k幅检索图像相关时为1，否则为0。对所有查询样本的平均精度求均值即为mAP。本实验中K在MS-COCO和NUS-WIDE的训练集上的值为5 000，CIFAR-10训练集上为54 000。

2.3 实验结果与分析

图3展示了测试集中随机抽取检索的4种类型图像。在CIFAR-10数据集上使用ACDH模型对训练集的检索结果进行可视化，从前K个检索图像中截取汉明距排序100～106的检索图像，在检索出的图像中第1行第7列为错误的检索结果，将鸟的图像归类到了飞机中。

从图3中可以看出，基于哈希的图像检索并不是一个简单的分类过程，因为对检索结果和待检索图的距离值进行了排序，在检索的结果排列靠前的图像中，目标物整体的颜色和形状特征会和左边的待检索图像很相似。以汽车和鸟为例，排名靠前的检索结果中大多数为白车和浅色背景的图片，而检索的鸟的图片为蓝羽灰色背景图像。

图3 图像检索结果示意图

在相同实验条件下，笔者对比了ACDH、DSH[5]、DFH[6]、DPSH[18]、HashNet[19]、DHN[20]、DTSH[21]和ADSH[9]等8种深度哈希方法在不同比特长度下的图像检索精度，结果如表2所示。

表2 ACDH和其他算法在3种数据集上的mAP性能比较

从表2中可以看出，笔者提出的ACDH模型在3种数据集上检索精度优于所有被比较的主流算法，并且ACDH在使用12 bit码长时的mAP值要高于DFH和DTSH等算法使用48 bit的mAP值。这表明在相同检索准确率的要求下，ACDH算法可以使用更短的哈希码实现。ACDH在NUS-WIDE数据集上的48 bit处，相比ADSH的性能提高了2.8个百分点，在MS-COCO上使用48 bit哈希码输出时，mAP检索精度值提高了2.1个百分点。在这两个复杂数据集上，ACDH算法的检索精度均获得了较大幅度的提升。

笔者通过消融实验分别验证了改进的深度网络SKNet-50和新的损失函数对整体模型的性能影响，将ADSH作为基准参考模型。实验结果如图4所示。

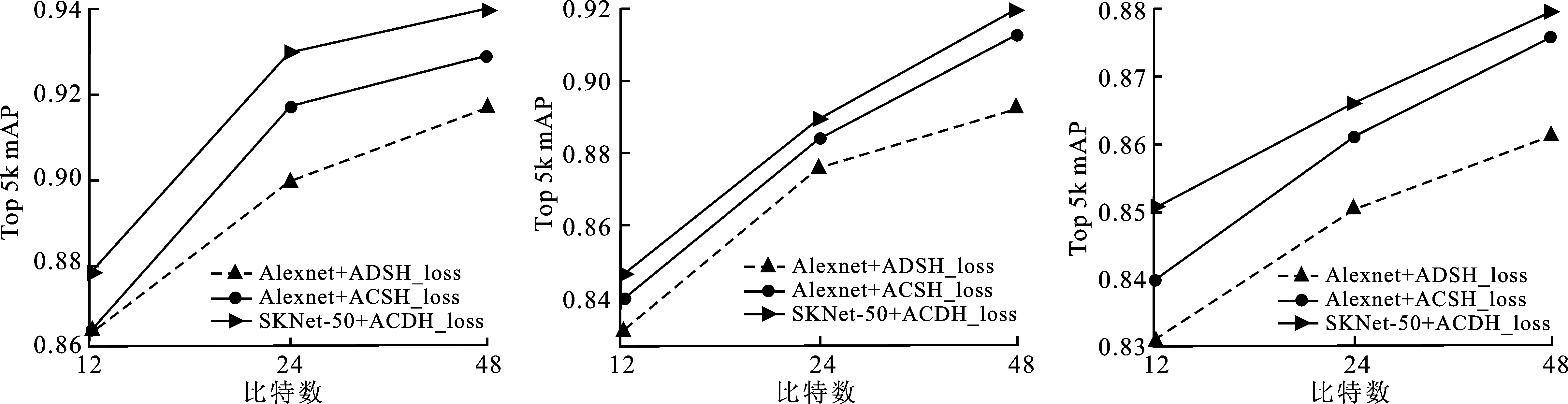
(a)CIFAR-10检索精度 (b)NUS-WIDE 检索精度 (c)MS-COCO 检索精度

ACDH模型在采用与ADSH相同的特征提取网络Alexnet时，仅在CIFAR-10数据集上映射12 bit哈希码时检索精度与ADSH持平，在其他情况下，检索精度均获得了较为明显的提高，印证了ACDH损失函数带来的性能提升。在使用SKNet-50作为主干网络时，相比采用了Alexnet网络的ACDH模型，在3种数据集上的检索精度均表现出了可观的提升效果。

从CIFAR-10数据集上随机抽取了1 000幅图像，在训练后的ACDH和ADSH在模型上映射为48 bit哈希码，利用t-SNE进行降维后的可视化结果如图5所示。在图5(a)中，图像经ACDH模型映射后的哈希码相比ADSH的图5(b)的结果，映射错误率更低。ACDH模型上表现的哈希码簇也更加紧凑，基本集中于较小的范围内，相邻图像类别所对应的哈希码簇相互之间始终保持固定的距离。ADSH由于并未对生成哈希码的距离进行约束，导致不同类别哈希码的分离程度不一致，映射在同类边缘的样本点更容易出现检索错误的情况，如图5(b)所示。

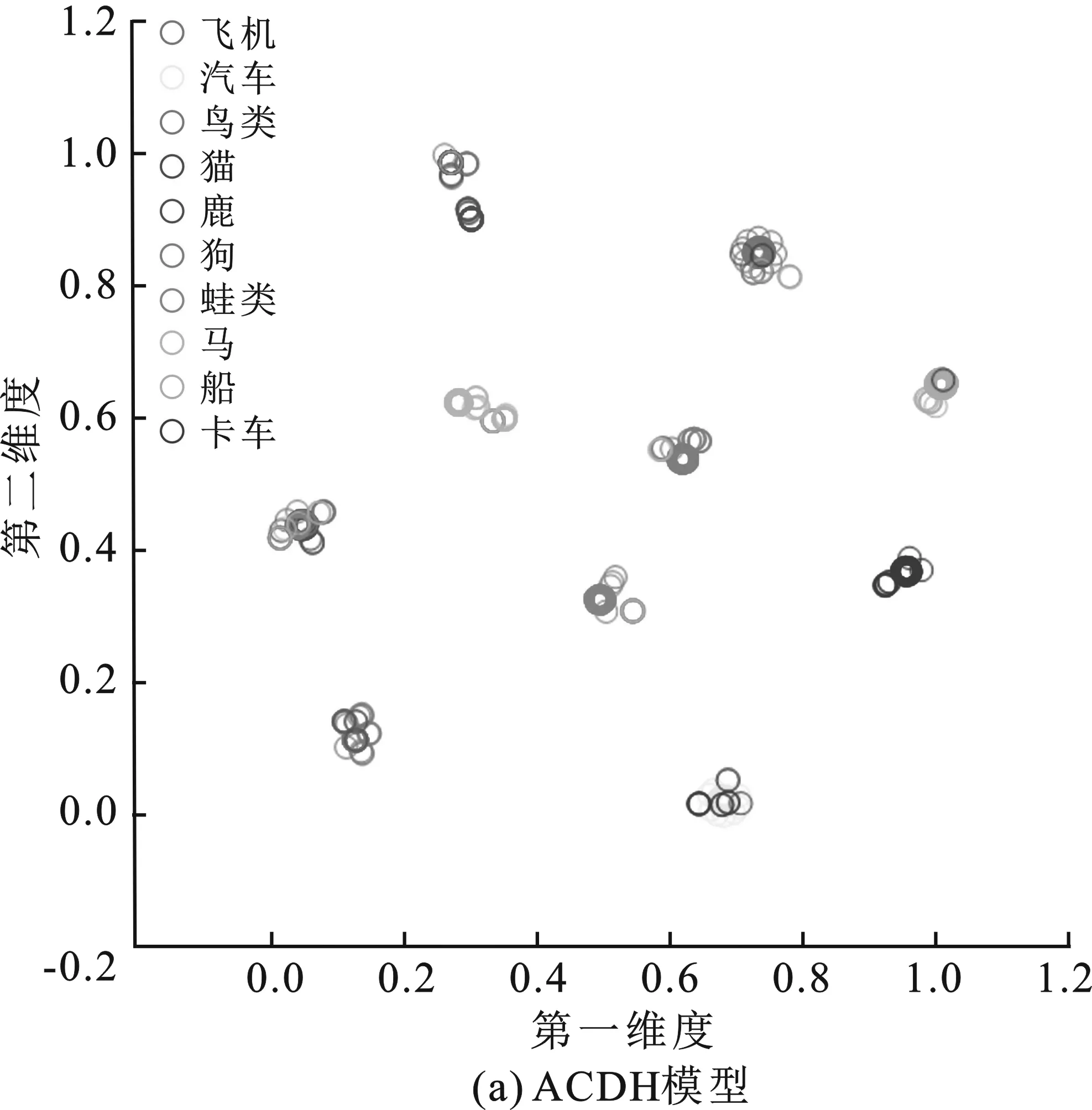
图5 使用t-SNE对两个模型结果进行可视化

2.4 参数对模型的影响

笔者对算法中超参数θ，ε，λ和查询集图像的数量m的影响做了定量分析，分别测试了4个参数对模型在CIFAR-10数据集上对精度的影响，结果如图6所示。

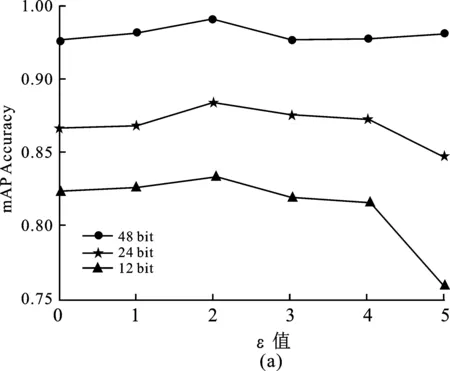
图6 参数对模型的影响

参数θ和ε共同影响着同类图像哈希码的聚拢程度。ε固定时，θ越小，生成的哈希码会越向中间靠拢；θ越大，生成的哈希码会向四周分离。参数ε控制着不同类型图像哈希码的分离程度，ε越大，不同类哈希码分离性会越高。由图6(a)和6(b)可知，θ和ε太大会对模型的训练精度产生影响，尤其对短的哈希码影响较大。系数λ是量化误差，控制着同索引下查询集哈希值U和数据集哈希值V的相似程度。λ值过高，会影响交替学习的进程。由图6(c)可知，λ=200时，模型的性能达到最佳。如图6(d)所示，当m>2 000后，模型性能会逐渐趋于平稳，但太大的m值会导致更高的计算代价。综上所述，参数θ设置为3，ε设置为2，λ设置为200，m设置为2 000。

3 结束语

笔者提出了一种基于非对称结构的深度哈希算法，通过端到端的网络对图像进行哈希编码。该方法将监督信息直接作用于离散编码过程，有效利用了数据库的全局监督信息。为了提高深度网络对图像表达能力，将改进的SKNet-50作为模型的主干特征提取网络输出哈希码；同时设计了一种新的损失函数，对生成哈希码的紧致性与分离性进行约束，增强了模型对困难样本的判别能力。使用ADMM算法完成了模型损失函数的不对称优化。在CAFAR-10，NUS-WIDE和MS-COCO三个数据集的上的测试表明，笔者提出的算法优于对比算法。