一种利用贝叶斯优化的弹道目标微动分类网络

李 鹏，冯存前，许旭光，唐子翔

(空军工程大学 防空反导学院，陕西 西安 710051)

随着多弹头分导以及诱饵技术大量应用在弹道导弹上，如何识别出弹头和诱饵成为各个国家反导系统研究的重点。微多普勒特征作为弹道目标的一个重要特性，广泛应用在弹道目标的识别上。早在1998年，美国海军研究实验室就对行人的雷达微多普勒特征开展了研究，一种基于微动特征的有效新途径开始在雷达识别领域得到应用[1]。弹道目标中常见的微动形式主要是旋转、进动、章动等。在弹道目标的中段飞行时，弹头一般会采用自旋的方式来进行姿态控制，由于在弹头和推进器分离时会受到冲击力距的作用，弹头总体会表现出进动的运动形式。而对于诱饵和其他的碎片，一般没有采取姿态控制，目标会呈现出章动的运动形式[2]。因此目标的微动特性作为弹道目标识别的有效依据，有必要对弹道目标的微动分类进行深入研究[3]。

为了对弹道目标的微动特征进行分类，很多学者对其进行了深入研究。文献[4]根据不同的微动形式时频图的周期性的强弱程度，提出用熵以及循环自相关函数与循环平均幅度差函数相结合的方法来判定其周期强弱程度，然后利用支持向量机分类器对其进行分类。文献[5]应用谐波和的形式描述回波信号，然后采用特征值分解提取特征谱作为识别分类的特征，提出用k近邻分类器进行分类。文献[6]首先提取微多普勒谱脊线，设定阈值来区分出自旋与进动章动的微动形式，然后根据微多普勒谱峰值是否等间距分布来对进动和章动两种微动形式进行分类。然而，弹道目标的微动特性周期规律性不明显，存在检测、提取和识别困难的问题，因此上述方法普遍存在识别精度不高，鲁棒性不强的问题。近些年随着人工智能的发展，深度学习被广泛应用在模式识别上。与传统的分类方法相比，基于深度学习方法的模式识别具有较好的泛化能力和识别精度，其在面部表情识别[7]、姿态感知[8]、图像识别[9-10]等领域均有大量应用并取得良好的识别效果。深度学习也被应用在弹道目标的特征识别上，文献[11]首先将弹道目标的高分辨距离像进行图像化，然后基于深度卷积神经网络对目标进行识别判定。文献[12]采用预训练的网络，利用迁移学习的技术更改AlexNet网络的全连接层和输出层，用来对弹道目标的微动特征进行分类。文献[13]根据分形理论把一维并行结构放到神经网络内，把不同深度的卷积层提取到的特征结合到一起以提高对弹道目标微动特征的提取和识别能力。上述的基于神经网路的方法在微动特征的识别精度上有显著的提升，然而在对神经网络的超参数和卷积深度的选择上往往靠过去的经验和大量的人工调试，很难得到最优的网络结构和参数，而利用迁移学习的网络其学习层还保留大量与源域有关的特征，对新任务的学习层次不深。

为了克服上述的网络的缺点，需要找到能够快速有效地得到适合于微动特征分类的网络参数和结构。笔者采用从头训练的方法训练卷积神经网络(CNN)，并用贝叶斯优化算法寻找最优的卷积神经网络的卷积层层数、初始学习率、随机梯度下降的动量以及正则化强度的数值。贝叶斯优化算法可在目标函数未知的情况下利用历史评估结果去建立目标函数的概率代理模型，能够在较少的优化次数中找到最优的优化参数。

1 弹道目标的建模与分析

采用文献[4]的等效散射点模型，对弹道导弹进行建模分析。选择圆锥作为弹头的几何模型。如图1所示，A，B，C为锥体弹头的3个强散射点，O点为质心，锥旋轴为Z轴，雷达视线为η，在雷达视线η与Z轴的平面上作OY轴垂直于Z轴，过O点作OX轴垂直于YOZ平面。记Z轴与雷达视线η的夹角为雷达视线角α，Z轴与锥体对称轴OA的夹角为章动角θ，OA在面XOY的投影OA′与OX轴的夹角为锥旋角φ。假设弹道目标已进行过平动补偿。

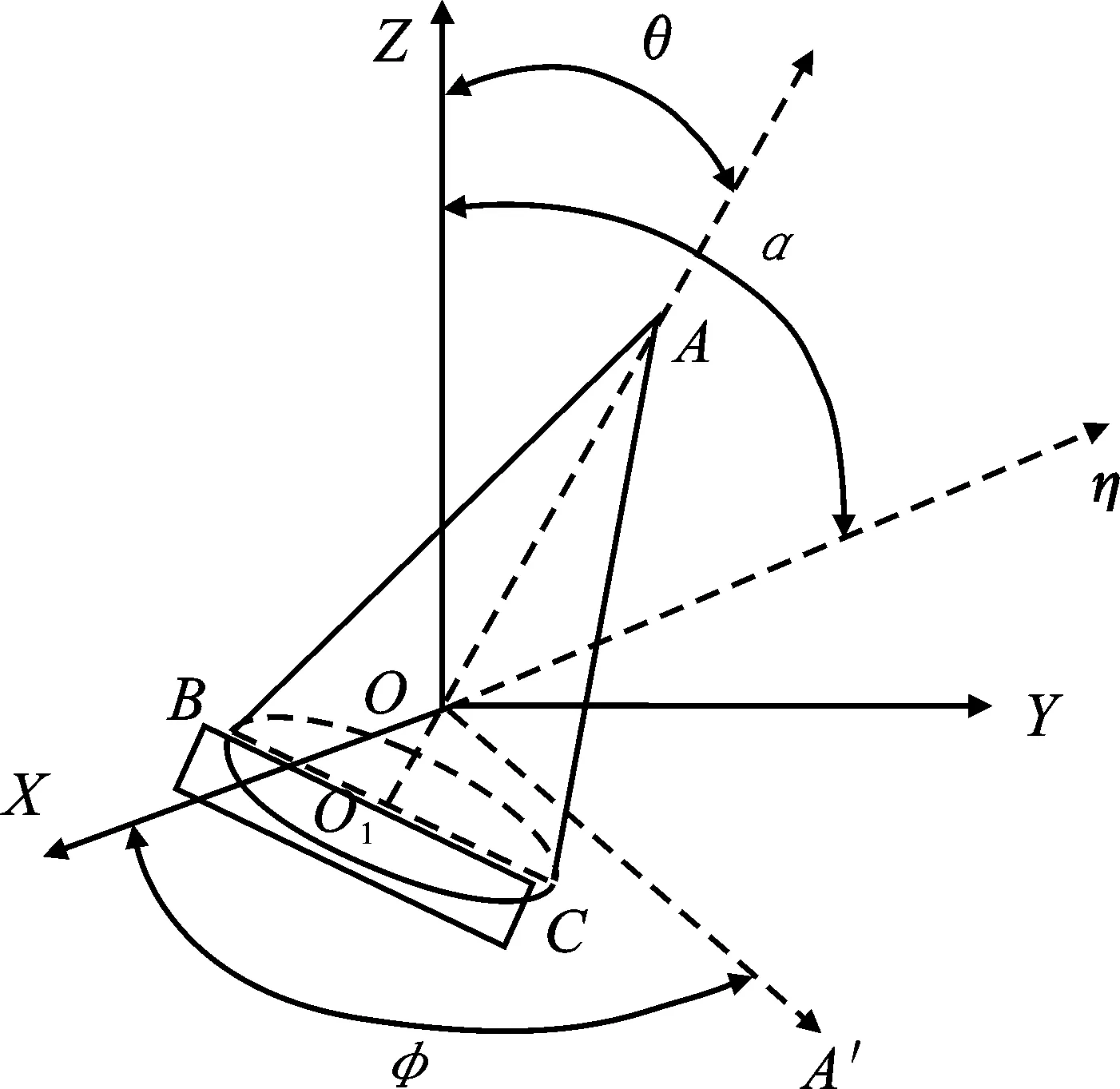
图1 弹道导弹弹头模型

雷达视线角η可以表示为

η=[0，sinα，cosα] 。

(1)

锥顶A在η上的投影为

rOA=lOA·η，

(2)

则锥顶A的微多普勒频率为

(3)

式(3)中，λ为雷达的波长。

下面推导滑动等效散射点B，C的微多普勒频移表达式。设雷达视线η和锥体极轴OA所在的平面为π1，锥体底面所在的平面为π2，B，C两点位于平面π1与π2的交线上。平面π1的单位法矢量为

(4)

那么锥体底面中心O1到等效散射点B的单位方向矢量为

(5)

则锥底等效散射点B，C对应的矢量为

rB(C)=lO O1±n2r，

(6)

其中，r为锥体底面半径。等效散射点B，C在雷达视线上的投影为

lB(C)=rB(C)·η，

(7)

则B，C两点对应的微多普勒频率为

(8)

根据锥体目标在不同运动状态的锥旋角φ和章动角θ的变化规律，可得到锥体目标在旋转、进动、章动时的微多普勒频率表达式。具体推导过程及结果可参考文献[4]。

2 数据集的构建及卷积神经网络初始结构

2.1 数据集的构建

以节1的平底锥体为模型，分别模拟弹道导弹自旋、进动、章动3种不同微动形式宽带雷达回波。假设宽带雷达发射线性调频(LFM)信号，带宽为2 GHz，载频为10 GHz，脉冲重复频率(PRF)为1 024 Hz。设平底锥的高O1A为3 m，质心到底面的距离OO1为0.75 m，底面半径为0.64 m。微动参数为：自旋时，雷达视线角α为95°～150°，章动角θ0为12°～20°，初始锥旋角φ0为18°～360°；进动时，雷达视线角α为95°～150°，章动角θ0为12°～20°，初始锥旋角φ0为0°，锥旋角频率fφ为0.84～1.20 Hz；章动时，雷达视线角α为95°～150°，章动角θ0为12°～20°，初始锥旋角φ0为0°，章动角摆动角度θ1为10°，锥旋角频率fφ为0.84～1.20 Hz，章动角摆动频率fθ为1.0～1.5 Hz。设置参数如表1所示。

表1 微动参数设置

除了上述的变量外，在仿真的过程中数据集还分别加入了信噪比为-15 dB∶5 dB∶15 dB的高斯白噪声。由此方法一共得到7×3×1 300张不同的时频图。同一信噪比情况下，每类微动形式产生1 300张不同的图像以用作训练测试网络的数据集，图像的分辨率大小为227×227×3，得到的部分图像如图2和图3所示。

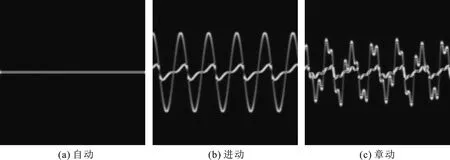
图2 无噪声条件下的时频图

图3 信噪比为-10 dB的时频图

2.2 贝叶斯优化算法

在机器学习中，几乎所有的优化问题都是黑箱优化问题，其需要找到最小绝对值的目标函数，但没有一个确定的表达形式，其导数也无法求出[14]。对于卷积神经网络模型超参数的优化，也是将卷积神经网络模型整体视为一个黑箱。超参数优化问题可以假设为：在一组超参数组合中X={x1，x2，…，xn}(xn表示第n个超参数的值)，对每一个超参数进行评估，评估的结果可以表示为f(xn)。在优化的过程中，需要找到最优的超参数x*：

(9)

其中，x*表示为使目标函数最小的参数值，x∈X。

人工选择相关的超参数进行调优非常困难，并且需要花费大量的时间。这就需要一个算法能够自动地找到最优的超参数。笔者基于贝叶斯优化算法，对卷积神经网络模型的超参数进行优化。贝叶斯优化算法是基于目标函数的历史评估结果去建立目标函数的概率代理模型，在选择下一组超参数的时候充分利用了之前的评价信息，减少了超参数的搜索次数，得到的超参数也最有可能是最优的，从而可以提高模型的估计精度和泛化能力。

贝叶斯优化是由贝叶斯定理导出的一种方法，用于搜索目标函数的最小值。根据贝叶斯定理，给定观测点E，模型M的后验概率P(M|E)与观测点E的似然比概率P(E|M)乘以模型M的先验概率P(M)成正比，即

P(M|E)∝P(E|M)P(M) 。

(10)

贝叶斯优化背后的思想是利用目标函数f(x)的先验分布以及之前训练模型的试验得到的观测点，来获得模型的后验分布。然后利用后验信息选择下一个样本点，使f(x)减小到最小[15]。

贝叶斯优化算法有两个核心的部分，概率代理模型和采集函数[16]。概率代理模型是指用来表示未知目标函数的概率模型，通过增加试验次数，不断地对目标函数的先验概率进行修正，从而使得表示未知目标函数的代理模型更加准确。采样函数根据后验概率分布，在最可能出现全局最优解的区域和还未采样的区域进行采样，从候选集中选择出最优的样本点，使得目标函数值最小。

在概率代理模型的选择中，高斯过程是一个很好的选择。高斯过程(Gaussian Processes，GP)是一种常见的非参数概率代理模型。高斯过程可以生成高维的高斯分布，能够模拟任何形式的目标函数[17]。在求出概率分布后，需要采样函数寻找下一个样本点进行样本计算。目前主要的采集函数有3种：Probability of Improvement(PI)，Excepted Improvement(EI)，GP Upper Confidence Bound(GP-UCB)[18]。笔者选择高斯过程和EI函数作为概率代理模型和采集函数。

2.3 卷积神经网络结构的搭建

一个典型的卷积神经网络模型包括输入层、分类输出层和隐藏层。隐藏层包括一系列的卷积层，然后是批处理归一化层和ReLU层，最后是池化层。为了使卷积神经网络模型能够充分地学习到图像的特征，将隐藏层分为3部分：第1部分隐藏层学习底层特征，接下来的部分依次学习中层和高层特征。每一部分由相等的块数组成，定义块数(部分深度)为n，其中每一块由一个卷积层、一个批处理归一化层和一个ReLU层组成。在每一部分后连接一个最大池化层，将空间维度下采样至一半。在隐藏层后依次连接全连接层和分类层组成的输出层，把学习的特征从高维降到低维，进行分类的显性表达。卷积神经网络的架构如图4所示。

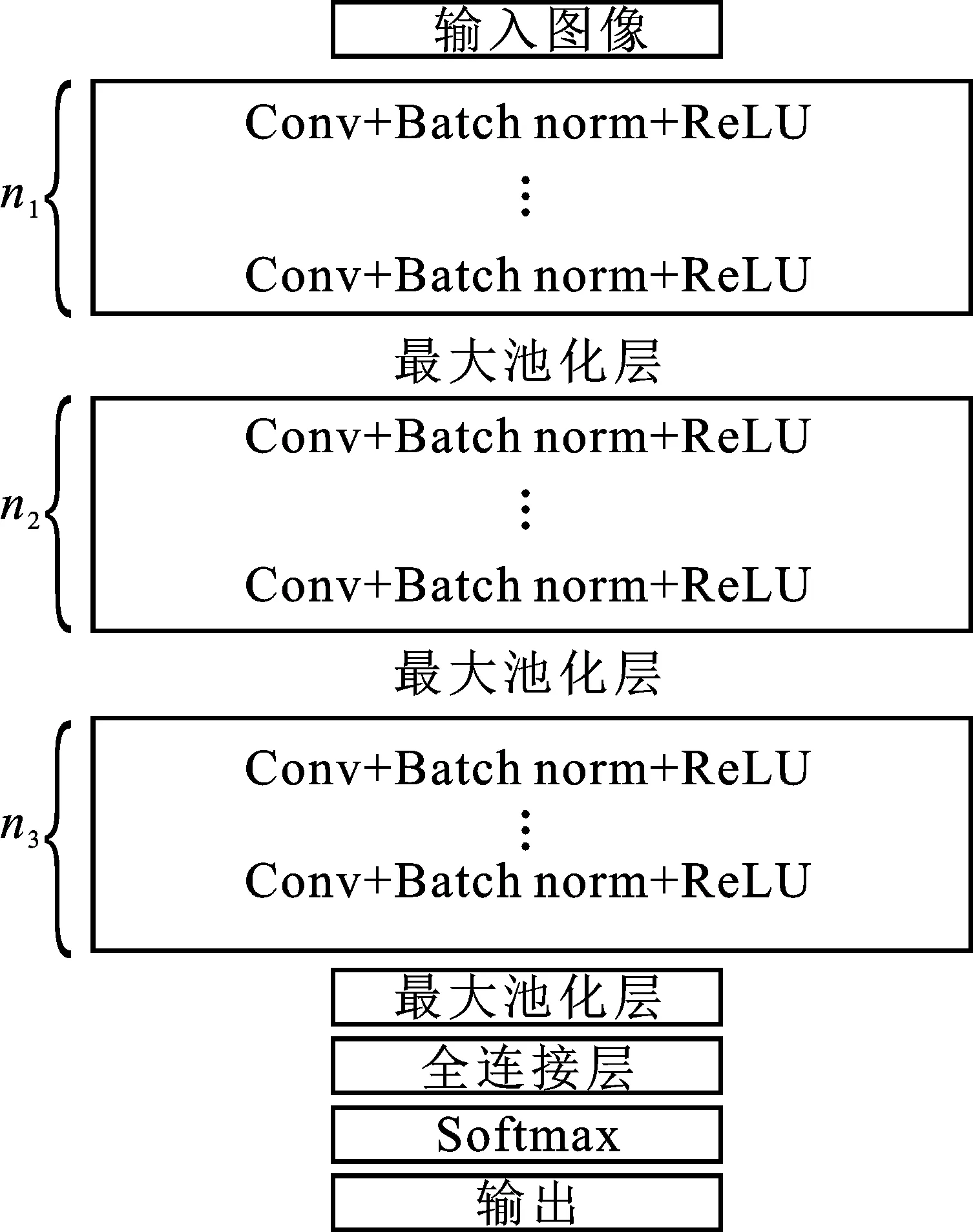
图4 卷积神经网络架构

在网络参数的选择上，因为仿真产生的时频图的大小是227×227×3大小的图片，因此输入层为二维图像输入层，输入层的图像参数设置为227×227×3。每个部分的卷积核(滤波器)的数量设置为与部分深度的平方根成反比。对于每次迭代，无论贝叶斯优化评估的网络模型之间的部分深度是否相同，参数数量和计算时间几乎是相等的。每次根据最大池化层将空间缩小1/2时，卷积层滤波器的数量就会增加1倍。这确保了每个卷积层的计算量几乎相等，因为卷积层越深，网络需要学习的特征就越多。网络各部分的卷积层滤波器的数量N可以表述为

(11)

其中，β为任意值，设置为10；n代表部分网络深度；ε为部分网络的排列顺序，依次为1，2，3。

本次实验的微动形式为3种，因此把全连接层的卷积核数量设置为3，输出可以将时频图划分为自旋、进动、章动3种不同的类别。

3 贝叶斯算法的卷积神经网络模型优化

3.1 卷积神经网络模型优化过程

卷积神经网络的基本架构以及训练的选项需要在训练之前进行设计，找出这些超参数以最小化匹配误差和避免过拟合不是一项简单的任务，如果在获得满意的匹配结果之前决定使用人工的方法搜索，则它会消耗大量的计算时间。笔者通过贝叶斯优化来自动调整超参数，在有限的搜索次数内达到最优值，从而保证得到最好的卷积神经网络模型。结合上一章中介绍的贝叶斯优化算法，利用贝叶斯算法优化训练卷积神经网络的流程如下：

步骤1 把得到的时频图数据集分为训练集、验证集和测试集，图像数量比例为0.7∶0.15∶0.15，即训练集、验证集和测试集的图像数量分别为910张，195张和195张。

步骤2 指定要优化的变量，优化的变量为卷积神经网络的超参数和网络结构本身的参数。

步骤3 定义目标函数FJ，将优化变量的值作为输入，利用数据集训练指定的网络，并用验证集进行验证。为了使此模型能够在不同的信噪比条件下具有较强的泛化能力，选择不同信噪比的数据集分别训练网络。同时以验证集上的错误概率作为目标函数FJ，然后保存训练后的网络。本次实验以0 dB的数据集为例说明网络的优化过程。

步骤4 通过将验证集上的错误概率最小化来执行贝叶斯优化。

步骤5 将得到的最优的网络参数加载到网络中，利用测试集上的数据对网络进行评估。

在步骤2中，选择优化变量时，需要指定变量的搜索范围和数据类型。在卷积神经网络的结构和超参数中，笔者选择对网络影响比较大的4个变量进行优化。

(1)网络的部分深度n。每个部分具有n个相同的卷积层，卷积层的总数为3×n。神经网络的深度影响对输入特征的抽象程度，然而神经网络的深度并不是越深越好，针对不同的任务需要找到合适的深度。

(2)网络的初始学习率LR。神经网络的学习率指的是神经网络对数据进行学习的速率。如果学习率过小，则可能会导致局部最优；如果学习率过大，则可能导致无法收敛到最优。最佳的学习率由使用的数据集和网络模型共同决定。

(3)随机梯度下降的动量MT。动量通过使用当前更新包含与上一次迭代中的更新成比例的贡献，来为参数更新增加惯性。这样可以使参数更新更加平滑，并减少随机梯度下降所固有的噪声。

(4)L2正则化强度RS。正则化可以防止神经网络过拟合现象的发生，通过搜索正则化强度的设置区间以找到一个合适的值。

上述的4个优化变量相互影响，任意一个参数的变动都会导致其他参数的效果发生变化，因此需要找到全局最优的参数设置。

在参数范围的设置上，根据以往的经验确定优化变量的搜索区间，如表2所示。

表2 优化变量的搜索区间

确定完优化变量及搜索区间之后，为了充分利用贝叶斯优化的能力，设置对目标函数进行30次评估。在每一次训练过程中设置验证频率为10，最小训练批次为64，求解法为随机梯度下降法，并把每次评估的结果显示出来。在贝叶斯优化过程中，每次观测到的函数值、计算时间、最小目标值如图5所示。实验条件：软件MATLAB 2020b，计算机配置i7-10750H，GTX1650 4 GB显卡。

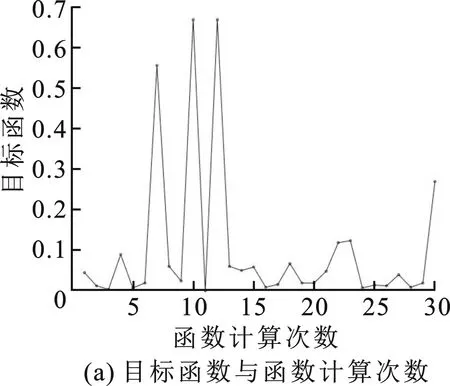
图5 贝叶斯优化过程

在对目标函数进行30次的贝叶斯优化评估中，得到了最优的可行点，最优的参数数值如表3所示。在此参数下，目标函数的值为0，即此参数下的卷积神经网络模型对微动特征的识别性能在验证集上的错误概率为0。

表3 最佳的卷积神经网络参数

3.2 模型优化结果

根据上一节中得到的优化结果，得到卷积神经网络模型的最终结构如图6所示。其中第1层为图像数据的输入层，其输入的图像数据大小为227×227×3，用来读取数据集中的时频图；在网络的最后为全连接层和分类输出层，用来将网络的计算结果转化成每一种类的概率，并将最大概率的结果当作识别结果作为网络的输出。在每一个网络层上显示了这一层网络的输出大小以及在卷积层和池化层的滤波器的大小。

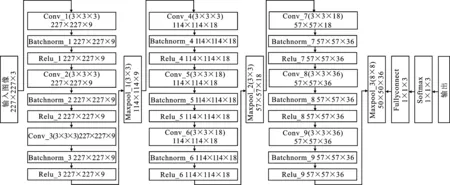
图6 贝叶斯优化得到的网络结构

接下来，将贝叶斯优化过程中找到的卷积神经网络模型在测试集上进行测试。由于贝叶斯优化是利用验证集得到的错误概率，从而确定最优的网络。然而测试集并没有暴露给网络，所以在测试集上的错误概率可能会大于验证集。如图7所示的测试集混淆矩阵，从图中可以看出，得到的最优化卷积神经网络模型在识别旋转、进动、章动3种微动形式时，正确率分别为100%、95.9%、95.9%。由于自旋形式的微动特征的比较明显，所以识别率最高，对微动形式的平均识别率为97.3%。

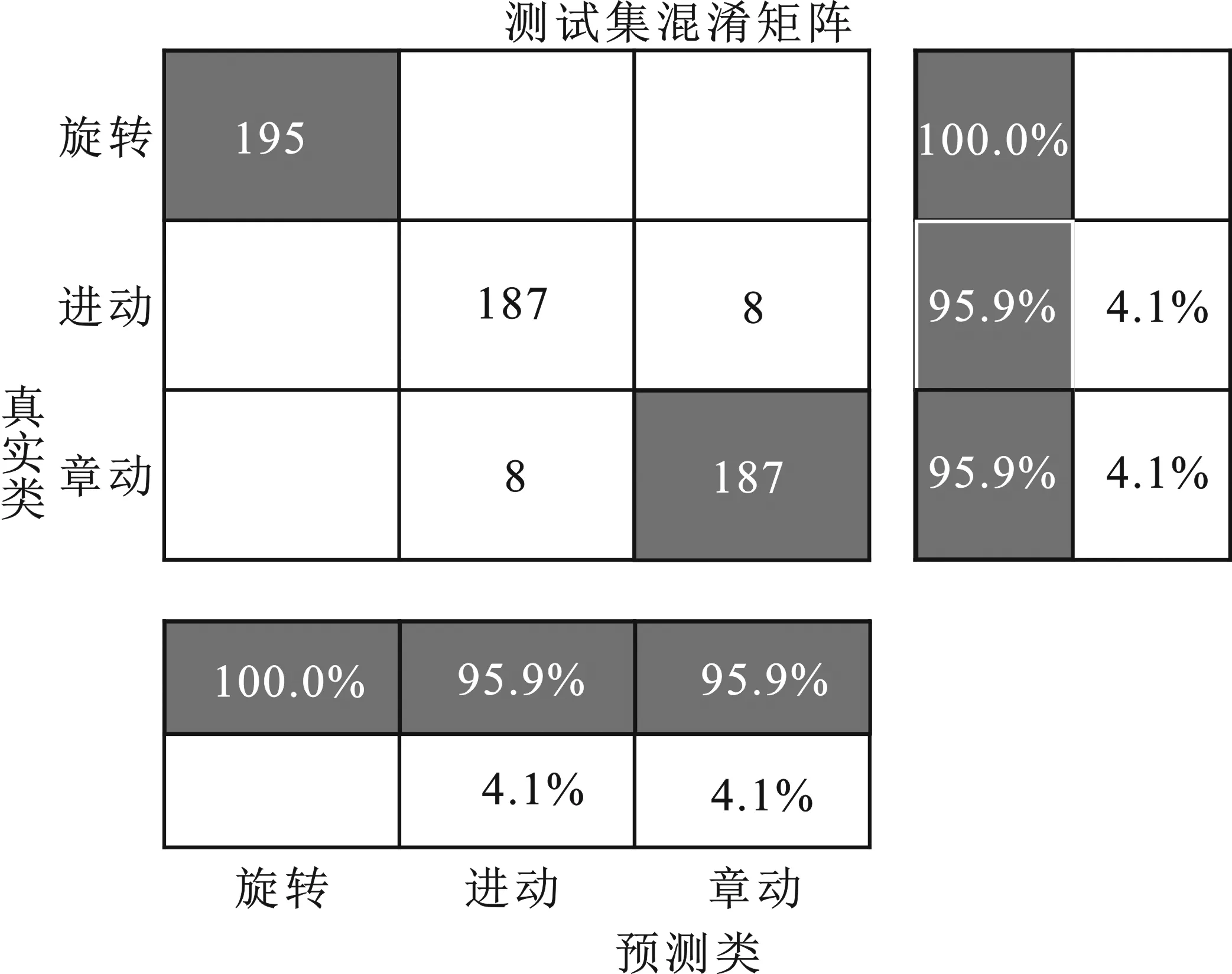
图7 测试集混淆矩阵

4 实验结果及分析

4.1 卷积神经网络的t-SNE分析

前面得到的卷积神经网络模型能够正确分类绝大多数的样本，但图像的哪些特征导致该网络做出的这种判断需要深度研究。卷积神经网络及许多其他深度学习模型常被认为是一种难以解释的“黑箱模型”，即无法了解卷积层提取的特征的本质。笔者采用t分布随机邻域嵌入(t-Distributed Stochastic Neighbor Embedding，t-SNE)算法[19]来可视化卷积神经网络的激活情况，从而分析卷积神经网络的响应方式。t-SNE技术可以将高维数据(例如某层的网络激活)映射到二维，它本质上是一种非线性降维方法。图8所示为用t-SNE技术展示的卷积神经网络模型中的第2个最大池化层，最后一个卷积层和最后的Softmax层的t-SNE数据。其中黑色、深色和浅色的点分别代表了旋转、进动和章动的二维特征。卷积神经网络模型中靠前的层倾向于对边缘和颜色等低级特征进行操作，而更深的层已经学会了包含更多语义信息的高级特征。从图8中可以看出，随着网络深度的增加，更深层的激活趋向于将来自同一类的点聚集在一起。

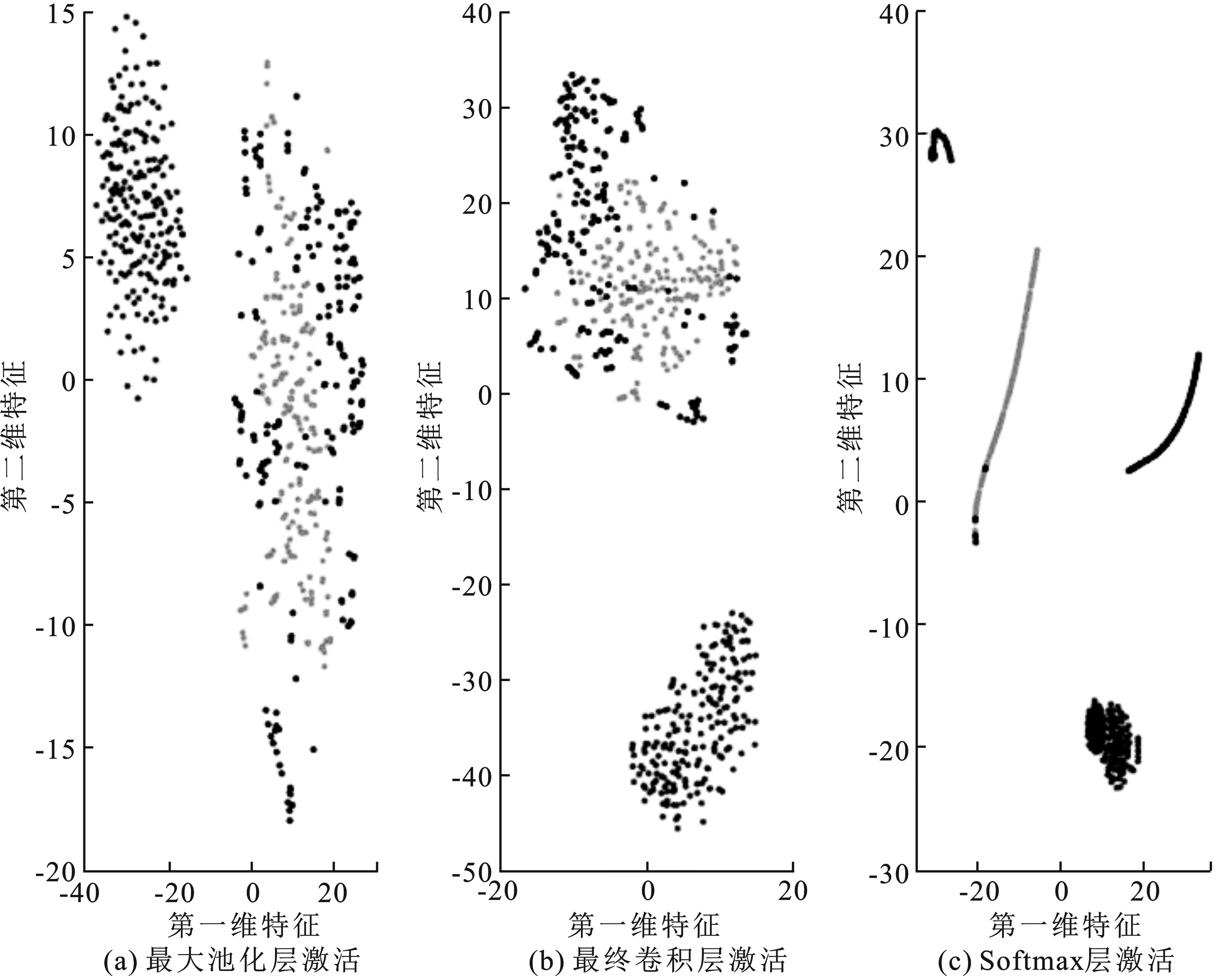
图8 t-SNE分析结果

在Softmax层的激活空间中，图像越相似其距离就越近，则不同类别的相似图像就容易导致误分类。在图7中，根据t-SNE展示的结果，其中旋转的二维特征和进动、章动的特征有很明显的区分，然而进动、章动的二维特征由极少量的数据混在一起，这也就解释了为什么识别旋转微动形式时正确率为100%，而识别进动与章动两种微动形式时，正确率为95.9%与95.9%。

4.2 分类性能比较

为了验证贝叶斯优化算法对卷积神经网络模型的影响，将有无贝叶斯参数优化作为变量。在无贝叶斯优化的网络，其结构与有贝叶斯优化的网络的结构保持相同，网络参数选择默认参数，即LR=0.01，MT=0.8，RS=0.000 1。在不同的信噪比下用数据集训练网络，得到的综合识别率对比如表4所示。从表中可以看出，在不同的信噪比下，与无贝叶斯优化的卷积神经网络相比，经过贝叶斯优化的卷积神经网络具有更高的识别精度。

表4 有无贝叶斯优化的网络识别性能对比 %

为了进一步验证文中网络在不同信噪比情况下的有效性和实时性，利用经典的Alexnet、GoogleNet和SqueezeNet网络模型，运用迁移学习的方法对微多普勒特征在不同的信噪比下进行训练，同时设置3种网络的超参数为默认参数。将不同信噪比下得到的数据集按照70%、15%和15%的比例随机分为训练集、验证集和测试集。同时，为了测试网络的数据处理能力，将4种训练好的网络在同一电脑环境下识别1 000张数据集中的时频图，记录下每种网络所花费的时间，然后就可以得到网络每秒的图像处理帧数。图9和表5分别给出了Alexnet、GoogleNet、SqueezeNet和文中网络对不同形式的微多普勒时频图的识别性能和识别 1 000 张图像所需要的时间。

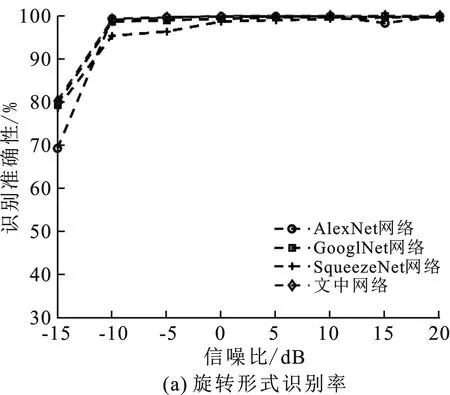
图9 不同网络微动特征识别性能

表5 不同网络的数据处理能力对比

分析图9和表5中的数据可知：

(1)在不同网络识别3种微动特征时，旋转形式的微动特征的识别率最高，这是因为旋转形式的微动特征与其他两种的微动形式具有较大的差异，特征较明显。

(2)在信噪比较大的情况下，4种网络都有很好的识别性能，识别率可以达到100%。随着信噪比下降，导致目标的微动特征减弱。基于迁移学习的网络由于其学习层的特征大多数为源域的特征，而基于贝叶斯优化的卷积神经网络学习层特征为微动数据集上的特征，因此在低信噪比的情况下，基于贝叶斯优化的卷积神经网络具有更好的识别性能。在信噪比为-15 dB的情况下，综合识别率比Alexnet、GoogleNet和SqueezeNet网络模型分别高出9.8%、7.3%和5.6%。

(3)在综合识别率的对比上，文中网络在不同的信噪比情况下的识别率都是最高的。可以得出结论，这种网络由于深入学习了不同微动形式的时频特征，因此与其他迁移学习的卷积神经网络相比具有较强的鲁棒特性。

(4)文中的网络在识别效率上高于GoogleNet，略低于Alexnet和SqueezeNet网络。

从上述对比中可以得出结论，文中网络与传统的方法相比，具有更高的精度和鲁棒性，对于识别精度和鲁棒性要求比较高的应用环境，卷积神经网络比较适合。

5 结束语

笔者研究了基于深度学习的弹道目标微动分类的方法。为了避免人工方法寻找网络的结构和超参数，提出利用贝叶斯优化的方法自动寻找最优的结构和超参数的方法。利用贝叶斯优化算法在30次迭代中成功地找到了最优的网络结构和训练方案。基于贝叶斯优化算法得到的卷积神经网络结构相比于支持向量机和微多普勒脊线方法具有更高的识别精度。在不同信噪比条件下，相比于基于迁移学习的Alexnet、GoogleNet和SqueezeNet网络模型具有更好的鲁棒性，其综合识别率均高于上述3种网络模型。仿真结果表明，笔者提出的方法为弹道目标的智能化识别提供了一种综合性能更好的卷积神经网络和网络设计思路。