基于CEEMDAN-DFA与FCM聚类算法的大地电磁强噪声识别与抑制

2021-11-12史维严良俊谢兴兵周磊

长江大学学报(自科版) 2021年5期

史维，严良俊，谢兴兵，周磊

1.油气资源与勘探技术教育部重点实验室(长江大学)，湖北武汉 430100 2.非常规油气省部共建协同创新中心(长江大学)，湖北武汉 430100 3.长江大学工程技术学院，湖北荆州 434020

大地电磁测深(magnetotelluric sounding，简称MT) 法是一种通过研究大地对天然交变电磁场的频率响应来获取地下不同深度介质电性特征分布的电磁勘探方法。MT法作为一种重要的地球物理勘探方法，现已被广泛应用于油气田勘探、深部找矿、地热资源调查、地震监测、深部地质构造研究等众多领域[1-3]。MT法以天然场为场源，天然电磁场具有能量弱、幅度变化大、频带范围宽等特点，野外实测信号常常容易受到各类噪声的干扰[4，5]。随着人类社会工业化进程的加快，噪声也越来越复杂，特别是强干扰地区(如矿山、城区)附近，噪声的幅值往往是天然信号的几倍甚至是几个数量级，导致采集数据的质量明显下降，并且很难将噪声与天然信号分离，致使后续的处理结果不能真实地反映地下介质的电性分布特征，从而影响整个勘探效果。因此，MT信号中的噪声抑制问题长期以来都是广大国内外学者长期关注和研究的热点之一。

近年来，如小波变换[6，7]、经验模态分解(empirical mode decomposition，EMD)[8，9]、数学形态滤波[10]、压缩感知重构算法[11]、局域均值分解[12]等现代信号处理方法均被引入到MT信号噪声压制领域，对于MT数据质量的改善都取得了一定的效果。但是上述方法均是对含噪的MT数据时间片段进行整体滤波处理，缺少噪声识别环节，在压制噪声的同时会损失一部分缓慢变化的低频信息，导致过处理现象的产生。鉴于此，笔者尝试对含强噪声的MT数据运用CEEMDAN(complete ensemble empirical mode decomposition with adaptive noise，自适应噪声的完备经验模态分解)-DFA(detrended fluctuation analysis，去趋势波动分析)与模糊聚类算法相结合的技术进行噪声识别与噪声抑制来解决该问题，以期更好地改善实测数据质量。

1 CEEMDAN-DFA滤波方法

1.1 CEEMDAN

CEEMDAN是在EMD和集合经验模态分解(ensemble empirical mode decomposition，EEMD)基础上发展而来的。EMD不需要选择基函数，能够根据信号的时间特征自适应地将复杂信号分解为有限个频率由高到低分布的本征模态函数(intrinsic mode function，IMF)，是一种分析和处理非线性、非平稳信号的有效方法[13]。然而，当信号中存在间歇干扰和噪声时，EMD容易产生模态混叠现象，为了解决该问题，2009年WU和HUANG提出了EEMD方法[14]。EEMD虽然在一定程度上解决了模态混叠问题，但其弊端在于信号在分解过程中不能完全消除残余噪声、重构信号误差较大。在EEMD的基础上，CEEMDAN被TORRES等提出[15]，该方法在EMD分解的每一阶段添加自适应高斯白噪声，计算唯一的余量来获取各个模态分量，相较于EEMD，它具有更好的分解完备性、重构误差几乎为零、计算量小等优点。信号x(n)经CEEMDAN分解后，可以被精确地分解为k个IMF分量和1个残差r(n)，即：

(1)

式中：xi(n)为IMF分量；i=1,2,…,k。

1.2 DFA

在EMD和其改进的去噪算法中，如何判断某个IMF分量是信号主导还是噪声主导，是影响算法去噪效果的关键因素。通过人工判定的方式选择，需要一定的先验知识，且缺乏自适应性。DFA利用分形特性对信号的复杂性进行量化，提供了一个定量参数(标度指数α)来表示非平稳时间序列的自相关特性，是一种被成功运用于检测非平稳信号的长程相关属性的方法[16]。其计算步骤如下：

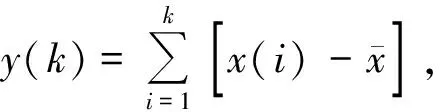
2)将y(k)不重叠地分为n个长度相等的窗口,对每一窗口，根据最小二乘原理，利用多项式拟合局部趋势项yn(k)来计算波动均方根F(n)：

(2)

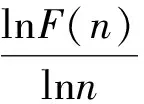
标度指数α可以作为识别噪声IMF的判别依据，具有可靠的评判标准[16]。当α=0.5时，说明时间序列不相关，如白噪声；当0<α<0.5时，表明时间序列呈反向相关，即小的波动后紧接着会出现大的波动，反之亦然；当0.5<α<1时，说明信号呈现相关性；当α≥1时，相关性不具有幂律性。因此，当α<0.5时，IMF的自相关性差，可以认为它是噪声；当α>0.5时，IMF具有长程相关性，即为有用信号。

1.3 仿真试验

MERT等[17]利用EMD-DFA对不同信噪比下的合成信号和真实信号进行去噪处理，效果优于软、硬小波阈值法。在此基础上，笔者采用CEEMDAN-DFA方法对含噪的MT信号进行滤波，选取小波分析中常用的piecewise-regular信号为原始信号，其采样率为4096Hz，时间长度为1s，添加信噪比(signal-to-noise ratio，SNR)为10dB的高斯白噪声得到含噪信号。

图1为含噪信号经CEEMDAN分解后所得的IMFs和残差(residual)，但从图中无法判断哪些IMFs是属于信号分量还是噪声分量。计算每一阶IMF(IMF1～ IMF12)对应的标度指数α，结果分别为0.386、0.219、0.214、0.308、0.531、0.900、1.450、1.760、1.948、1.986、1.996、2.012。基于之前的分析，将计算结果α>0.5的IMF判定为有用信号，CEEMDAN-DFA滤波结果应为IMF5～IMF12之和，其结果如图2(c)所示，此外图2还给出了小波阈值滤波(db6)和EMD-DFA滤波结果，分别如图2(d)、图2(e)所示，可以看出，相较于小波阈值滤波(db6)和EMD-DFA滤波，经CEEMDAN-DFA方法滤波所得的结果曲线毛刺明显减少，形态更加清晰、光滑，更好地还原了原始信号特征。

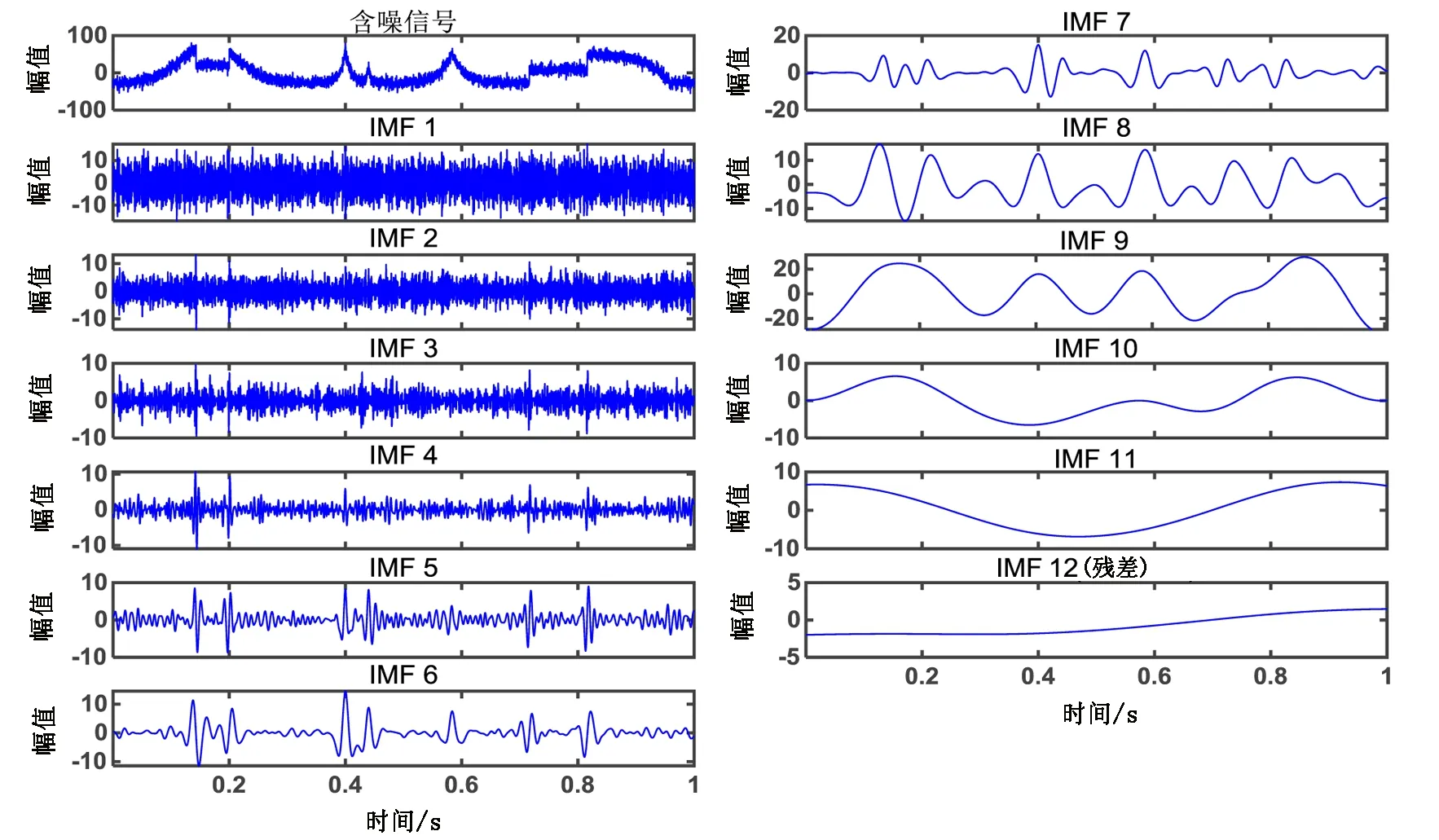
图1 含噪信号CEEMDAN分解过程Fig.1 Decomposition of the noise signal by CEEMDAN

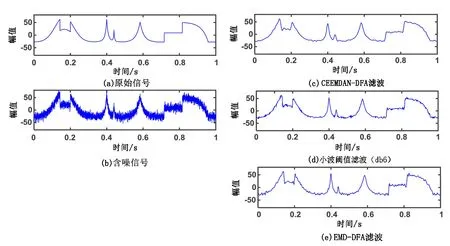
图2 SNR为10dB时3种方法滤波效果Fig.2 The filtering effect by three denosing methods with SNR=10dB

为了更加综合、客观地评价上述3种方法所获得的去噪效果，笔者对原始piecewise-regular信号加入不同强度的噪声，再分别利用上述3种方法对含噪信号进行去噪处理，并选用SNR、归一化相关系数、均方根误差3个指标参数对去噪效果进行评价，对比结果如表1所示。其中，在小波阈值方法中选择sym6和db6小波函数，分解层数为5层，阈值方式选用sqtwolog，阈值函数选用软阈值。分析表1可知，当含噪信号的SNR为20dB时，3种方法的去噪效果相差无几；然而，随着SNR的降低，经CEEMDAN-DFA方法的归一化相关系数更接近1，均方根误差最小。由此可见，在不同噪声强度背景下，上述3种方法中CEEMDAN-DFA方法的去噪效果是最好、最稳定的。

表1 不同噪声强度背景下3种方法去噪效果对比

2 基于模糊C均值聚类算法的噪声识别

模糊聚类算法是一种典型的无监督学习方法，它以模糊集合论为数学基础，其基本思想是将待分类的对象按照数据的特征分成若干类，使得划分为同一类的对象之间的相似度最大，而不同类之间对象的相似度最小[18]。模糊C均值(fuzzy C-means，FCM)聚类是模糊聚类中应用最为广泛的一种算法，该算法理论完备，聚类效果良好，已在图像处理[19]、机械故障诊断[20，21]等领域得到广泛应用。

特征参数的选定是数据聚类分析的首要问题，选择哪些特征参数作为聚类特征来使用，会直接影响到聚类效果。通过分析大量的实测MT数据可知，常见的强干扰有方波噪声、脉冲噪声、三角波噪声等，相较于随机的天然电磁场信号，这些噪声具有能量强、幅值大、形态特征明显等特点。鉴于此，笔者尝试从时间序列的复杂度与能量大小2个角度出发，选取模糊熵与短时能量2个特征参数作为聚类特征，并利用FCM聚类算法对实测MT数据中受强噪声干扰的部分进行识别。

2.1 模糊熵

模糊熵是陈伟婷等[22]在近似熵和样本熵概念的基础上提出的一种新方法，这3者具有类似的物理意义，都能衡量时间序列维数变化时产生新模式的概率大小。概率越大，则时间序列的复杂度越大，其熵值也越大；反之亦然。然而，相较于近似熵和样本熵，模糊熵具有更好的连续性、一致性和数据长度独立性，且不受基线漂移影响的特点[23]。

假定长度为N的时间序列为{u(i)：1≤i≤N}，模糊熵的计算流程如下：

1)对于给定的参数m，按顺序对时间序列进行相空间重构得到m维向量：

(3)

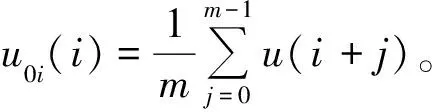
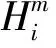
(4)

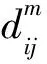
(5)

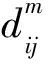
4)定义函数：

(6)

5)令m=m+1，重复步骤1)～4)可得φm+1(n,r)：

(7)

6)模糊熵FE定义为：

FE(m,n,r,N)=lnφm(n,r)-lnφm+1(n,r)

(8)

2.2 短时能量

能量分析用来反映信号能量随时间变化的情况，短时能量为一个短段(帧)的能量。目前，短时能量被作为一种识别语音信号与非语音信号的重要参数在语音信号处理中已得到了广泛应用[24]。鉴于MT信号与语音信号都属于非线性、非平稳信号，且天然MT信号和强噪声在能量特征上有显著区别。因此，选取短时能量作为模糊聚类算法的特征参数去识别MT有用信号和强噪声在一定程度上是可行的。

对MT时间序列进行不重叠分帧，第i帧短时能量E(i)公式为：

(9)

式中：ti(n)为第i帧时间序列，1≤i≤M；M为总帧数；L为每帧的长度。

2.3 FCM聚类算法

FCM聚类是传统硬聚类算法的改进，其基本思想是计算从所有数据到每个聚类中心的欧氏距离及模糊隶属度的加权和所确定的目标函数，通过反复修改聚类中心矩阵和隶属度矩阵使目标函数最小化，以达到将具有相似特征的数据对象聚为一类的目的[20]。

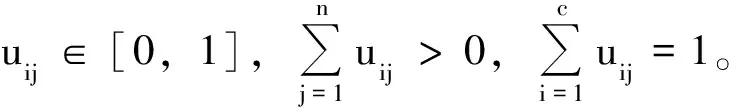
FCM的目标函数J(U,V)为：

(10)

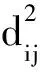
从式(10)可以看出，目标函数J(U,V)等于加权类内距离平方和，其值越小，表明样本离某个聚类中心越近。因此，FCM聚类算法的实质是使目标函数J(U,V)最小化来求解隶属度矩阵U和聚类中心矩阵V，具体步骤如下：

1)给定聚类个数c和加权指数m，初始化隶属度矩阵U=[uij]c×n，设定精度ε，令迭代次数l=0。

2)计算样本的c个聚类中心vi：

(11)

3)更新隶属度矩阵U：

(12)

4)当满足‖Ul+1-Ul‖<ε时，迭代停止，否则重新执行步骤2)、3)直到满足精度为止。

2.4 仿真试验

先选取内蒙古锡林浩特某工区几乎未受干扰的MT信号中的30个时间片段，然后再从受人为干扰严重影响的湖南某工区选取90个受典型强噪声干扰的时间片段(含矩形波噪声、含脉冲噪声及含三角波噪声干扰的时间片段各30个)，总共120个时间片段组成测试样本集。其中每个时间片段均包含150个采样点，从每种类型的信号中随机选取一个片段，波形如图3所示。

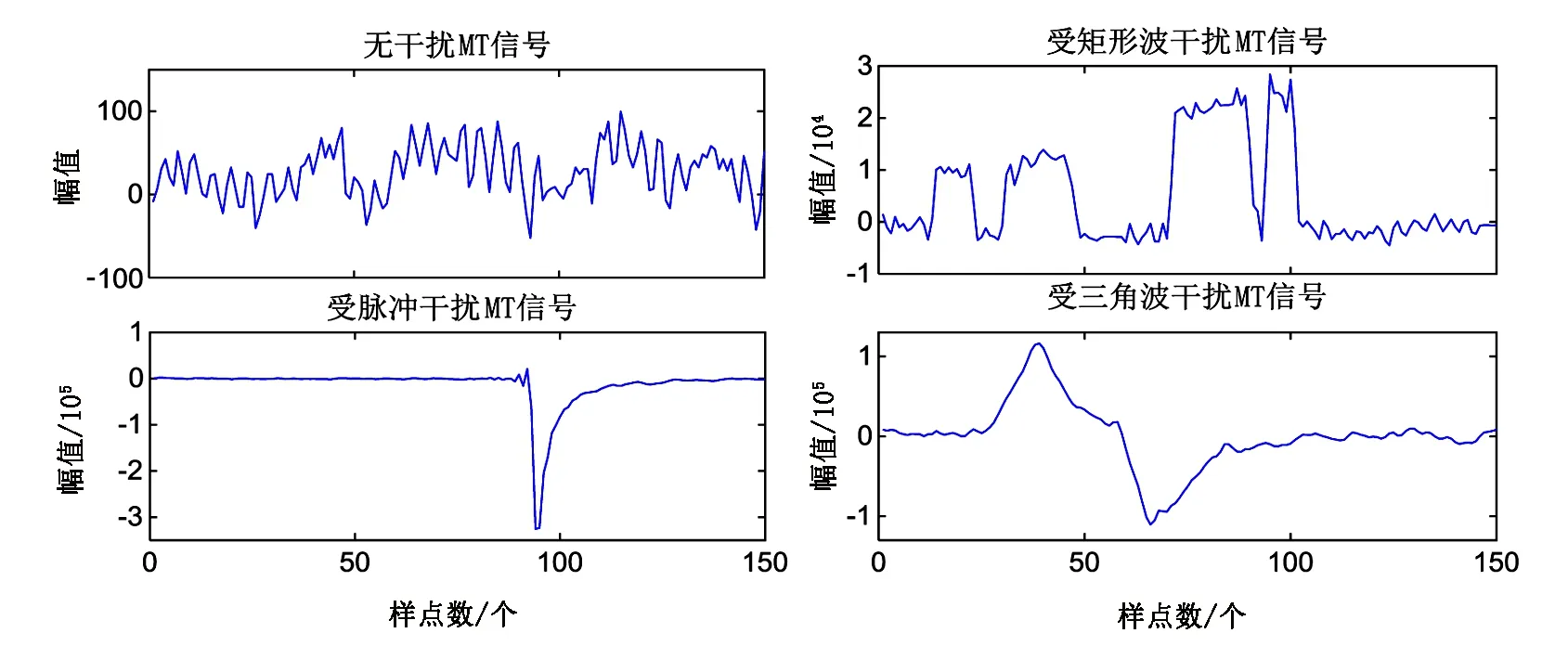
图3 各种实测MT信号时间片段Fig.3 Time domain waveform segments of various measured MT signals

计算120个样本的模糊熵及归一化短时能量，参数数值分布如图4所示。由模糊熵的定义可知，模糊熵的大小能反映时间序列的复杂程度。从图4可以看出，无干扰MT信号的模糊熵要大于受到强噪声干扰的3类MT信号的模糊熵，能很好地将无干扰和受强干扰的MT信号区分开，其原因是：无干扰的MT信号属于非线性、非平稳的随机信号，波形无规则程度较高，相对较复杂，故模糊熵较大，而受严重干扰的MT信号由于受到强噪声的影响，形态比较规则，复杂度较低，故模糊熵较小。由于实测MT数据幅值容易受到地域、基线漂移等因素的影响，从而导致数据幅值的数量级差异巨大，使得短时能量无法客观地反映信号能量随时间变化的规律。为避免上述因素所带来的影响，在计算短时能量之前需要对数据进行预处理，笔者采用去趋势项、标准差标准化的预处理手段使数据在同一尺度范围下进行计算分析，经预处理后计算的归一化短时能量结果如图4(b)所示。从图4(b)中可以看出，虽然受强干扰的3类MT信号曲线跳变、交叉现象比较明显，但与无干扰的MT信号并没有混叠，这表明归一化短时能量对无干扰和受强干扰的MT信号也有较好的区分度。

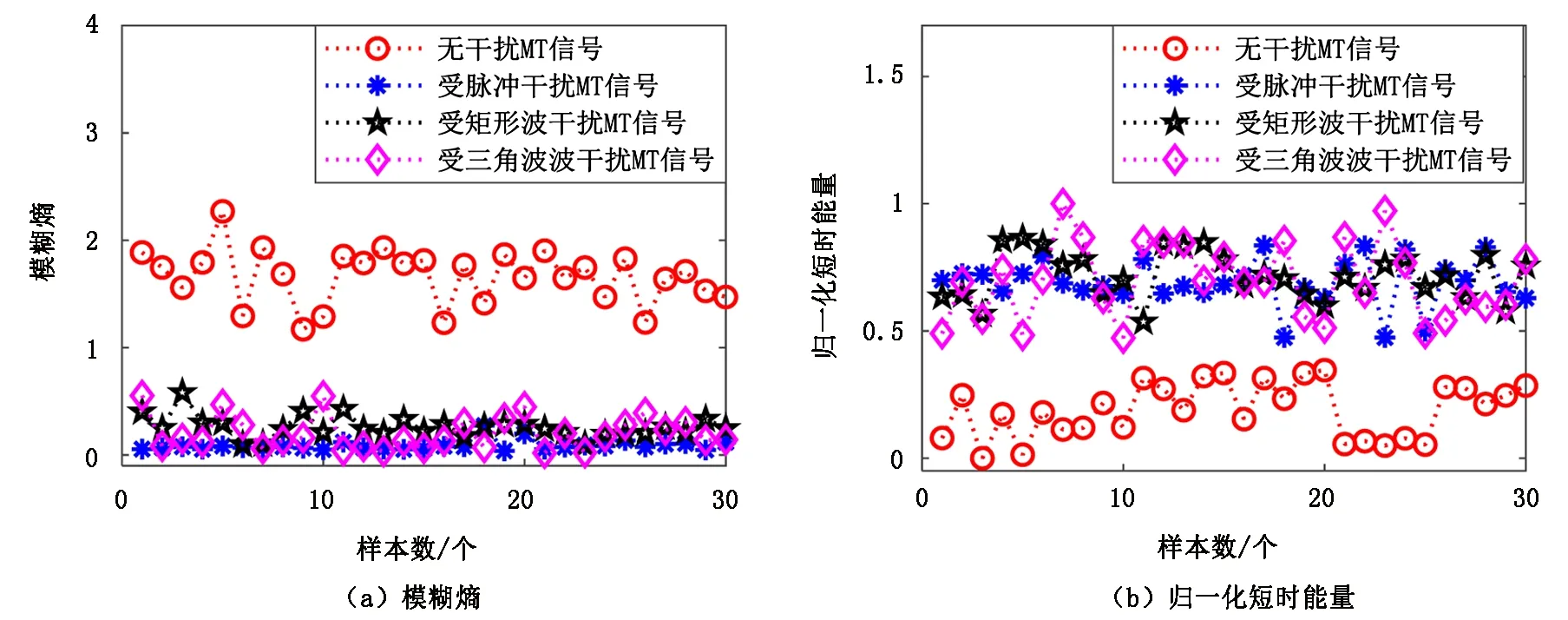
图4 特征参数数值分布Fig.4 Value distribution of characteristic parameters

图5 FCM模糊聚类结果Fig.5 Fuzzy clustering results by FCM

将模糊熵和归一化短时能量作为特征参数，并利用FCM算法进行模糊聚类，结果如图5所示，可以看出，30个未受干扰的MT信号样本分为一类，其他90个受强噪声干扰的MT信号样本则分为另一类，显现了良好的聚类效果。

3 实测数据处理

实测数据来源于湖南某地区受干扰严重的TYS2-31A测点的采集资料，采集仪器为加拿大Phoenix公司的MTU-5A。数据采样率为高、中、低3种频率，分别为2400、150、15Hz，采集数据分别保存放在TS3、TS4、TS5这3个文件中，每个文件均包含5个分量(Ex、Ey、Hx、Hy、Hz)。考虑到数据量巨大，为了便于解释说明与对比，仅选取该测点TS5文件的电场分量Ex和磁场分量Hy中受到矩形波、三角波干扰的2个时间片段，并利用传统的整体滤波和笔者所提方法分别进行处理，对其他噪声的处理方法也与之类似。

传统的整体滤波方法首先会对含噪的MT信号进行CEEMDAN-DFA滤波，提取强噪声整体轮廓，然后从含噪的MT信号中将强噪声剔除，得到重构的有用MT信号，结果如图6所示。分析图6可知，利用CEEMDAN-DFA方法进行整体滤波虽然可以较好地压制矩形波和三角波干扰所产生的影响，但重构后的MT信号仅在基线附近振动，原始信号表现出的整体波动趋势已不存在，表明原始MT信号中缓慢变化的低频信息在整体滤波过程中已被剔除，即出现了过处理现象，使得后续卡尼亚视电阻率计算结果中会出现低频信息的缺失，从而导致后续的解释结果无法客观地反映地下介质深部构造的电性特征。

笔者在传统整体滤波方法的基础上增加了强噪声干扰识别环节，使得滤波更具针对性，处理步骤如下：①对受干扰信号先进行整体滤波，保留滤波结果；②对原始信号进行不重叠分帧，每一帧数据为一个样本，样本长度为10s，即150个样点，并对数据进行预处理；③计算每个样本的模糊熵和归一化短时能量；④利用FCM算法对样本进行分类识别；⑤将识别为受到强干扰的数据段所对应的整体滤波结果与识别为未受干扰的MT信号组合作为最终的处理结果。

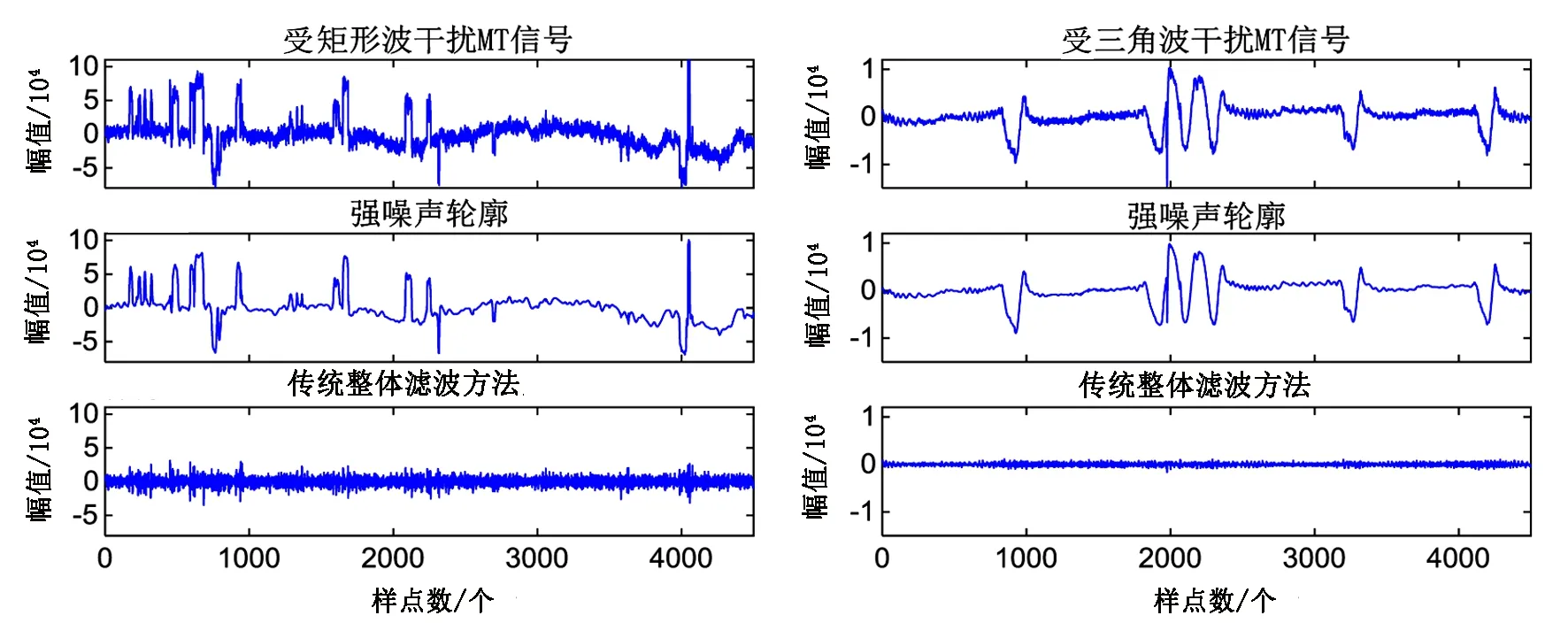
图6 实测数据传统整体滤波方法效果Fig.6 The effect of traditional integral filtering method for measured data

图7为实测数据传统整体滤波方法与CEEMDAN-DFA与FCM聚类算法的噪声识别及滤波结果对比。分析图7可知，CEEMDAN-DFA与FCM聚类算法可自动将受严重干扰和未受干扰的MT信号区分开，所得结果不仅能压制矩形波和三角波干扰的影响，而且能很好地保留原始信号中缓慢变化的成分。

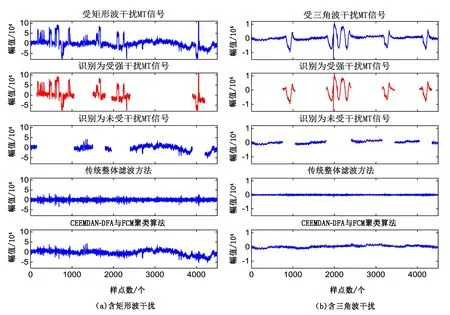
图7 实测数据传统整体滤波方法与CEEMDAN-DFA与FCM聚类算法的噪声识别及滤波结果对比Fig.7 Comparison of the noise recognition and filtering results between the traditional integral filtering method and CEEMDAN-DFA combined with FCM clustering algorithm for measured data

图8为经上述2种方法处理后所得结果的时频分布对比图，可以看出，经整体滤波处理后的结果在低频部分幅值出现快速下降的现象，说明该方法损失了有用的低频信息；而经笔者所提方法处理后的结果则较好地保持原始信号中低频部分能量分布的特征，表明该方法能更多地保留反映低频信息的细节成分。

注：lg(Amp)、lg(Fre)表示对幅值和频率取以10为底对数。图8 传统整体滤波方法与CEEMDAN-DFA与FCM聚类算法的时频分析结果对比Fig.8 Comparison of time-frequency analysis results between the traditional integral filtering method and CEEMDAN-DFA combined with FCM clustering algorithm