基于自编码器的零样本扣件检测

申瑞超，柴晓冬，李立明，孙 睿，钟倩文

(上海工程技术大学 城市轨道交通学院, 上海 201620)

0 引 言

铁路运输是一种能源集约式的陆地交通运输，因其运输量大、速度较快、受环境因素影响较小、安全性强等特点受到国家重点发展，截至2020年7月底，中国铁路运输总营业里程已超过14万千米[1]。在铁路运输中安全尤为重要，扣件作为钢轨与枕木的连接部件，扣件状态的检测在铁路运输安全中扮演着重要角色。扣件处于缺失、位移、断裂等失效状态时，可能会造成列车脱轨等重大安全事故。人工巡检是常用的扣件状态检测手段之一，但绵长的铁路线路和复杂的环境，耗费了巨大的人力和财力，工作人员的安全也得不到保障，利用机器视觉技术检测铁路扣件状态已成为趋势。如20世纪90年代，美国的VIS综合系统使用人工和计算机结合的方式对扣件、钢轨和道床等进行检测[2]；2016年，中国自主研发的综合铁路巡检车在昆明铁路局试用，实现了自动化检测钢轨表面和扣件，其对扣件状态检测的准确率达96%[3]。为了提高准确率，机器学习和深度学习应用到扣件检测中，如Khan R A[4]等结合脚点检测和模板匹配检测扣件；王强等[5]利用改进的LBP特征对扣件进行检测，提高了在不同环境下的检测的正确率；林菲等[6]采用深度学习网络VGG自动提取扣件特征，使得扣件检测的精度提升，达97.14%。然而，机器视觉算法的有效性是建立在数据分布大致均衡的假设基础上[7]，采集到的现场扣件图像正负样本往往不均衡[8]，这样的数据训练出的模型就会造成将负样本检测为正样本的情况。如Gibert[9]和李永波[10]在利用机器视觉算法检测扣件时，正负样本失衡，虽然在其各自提出的算法中做了验证，但是负样本较小的情况下的算法指标不能代表模型的泛化能力[11]，在现实应用中可能会造成漏报率较高的情况。为解决机器学习中样本不均衡问题，Nekooeimehr[12]等提出了一种加权训练方式，通过对少数样本的采样次数和权重进行自适应，实现不均衡样本的机器学习[12]。本文提出了一种基于自编码器的零样本扣件检测，只需要提供正样本，就可以达到检测扣件状态的目的。

算法流程如图1所示。首先，使用欠完备自编码器、栈式自编码器和卷积自编码器提取扣件正样本图像特征；通过正样本特征向量与基向量的余弦相似度推断出负样本的分布空间；在检测时将各自编码器算法得出的结果利用多数投票法确定样本属性。实验证明，使用本文方法，在只使用正样本训练的情况下，可以有效地检测出扣件图像的负样本，实现了零样本扣件检测。

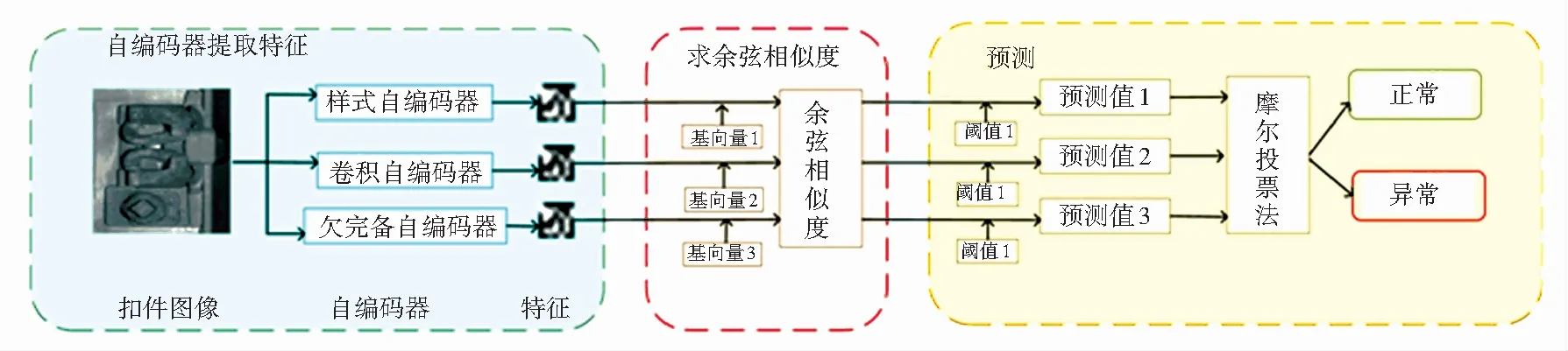
图1 算法流程图

1 自编码器

自编码器是前馈非循环神经网络，不需要借助事先标注的标签，通过无监督学习，学习到数据的高效表示[13]，具有非常好的提取数据特征的能力，在图像重构、聚类、机器翻译等方面有着广泛应用。自编码器的通用结构如图2所示，有输入层、隐含层和输出层，可以分为编码器部分和解码器部分[14]。假设自编码器的输入层输入为v，隐含层的输出为y，输出层的输出为s，则v和s有相同的维度，在训练时，通过调整自编器内部的参数，尽可能的让v和s的值相同，训练完成后，移除解码器，新的数据经过编码器前馈运算输出的值就是编码结果。

图2 自编码器通用结构

编码器通过式(1)将v映射为y，实现了原始数据的编码，解码器通过式(2)将编码数据y重构为s，实现数据解码。

y=f(v)=ξ1(w1v+b1)

(1)

s=g(v)=ξ2(w2y+b2)

(2)

其中，w1和b1是编码器的参数矩阵和偏置量，w2和b2为解码器的参数矩阵和偏置量，通过对w1、b1、w2和b2的调整，使v和s相同；ξ1和ξ2为映射函数。本文使用3种自编码器：欠完备自编码器、栈式自编码器和稀疏自编码器。

1.1 欠完备自编码器

欠完备自编码器的隐含层神经元数少于输入层，即s的维度小于v的维度。初始状态时，w1、b1、w2和b2都是随机初始化，通过最小化损失函数L实现s与v的值相同。假设v和s的维度为n，本文欠完备自编码器使用的均方误差(Mean Square Error，MSE)损失函数的表达式为：

(3)

其中，si表示输入图像的第i个像素值，vi表示解码器的第i个输出值。自编码器的参数用w表示，参数的更新如式(4)：

(4)

其中，η是学习率，通过链式求导法则更新自编码器中的每个参数使L(v,s)趋近于0，此时y就是v的低维度表示。

本文使用的欠完备自编码器如图3所示，隐含层使用49个神经元，输出层与图像维度相同，使用式(5)ReLu作为映射函数。

图3 欠完备自编码器

(5)

在训练时将扣件图像的每个像素依次排列，拉伸为211 600维的向量作为自编码器的输入，将输出值带入式(3)求得损失，并通过式(4)更新自编码器参数。

1.2 栈式自编码器

栈式自编码是一个由多层自编码器堆叠组成的神经网络，其前一层自编码器的输出作为其后一层自编码器的输入。对于一个k层栈式自编码的编码过程就是按照从前向后的顺序执行每一层自编码器的编码步骤。假设Hi表示栈式自编码器的第i层(0≤i≤k)，自编码器的隐含层Hi会作为Hi+1层的输入层，第一个输入层就是整个神经网络的输入层，利用贪心算法训练每一层的步骤如下：

准确称取25mg样品(样品粒度小于0.074mm)，加入0.2mL高氯酸和125mg氟化氢铵于消解罐中，盖上盖子(不要拧紧)，放入烘箱，升温至120℃，保温1h，然后升温到230℃，保温3h，冷却后取出消解罐，得到白色粉末状固体。于消解罐中加入2mL硝酸，拧紧盖子置于160℃电热板上加热1h，冷却后打开盖子，160℃蒸至近干状态，继续加入2mL 硝酸，升温至250℃继续蒸干，同时保温2h。取下消解罐，并冷却到室温，加入2mL 5%硝酸(体积分数)于消解杯中，于电热板上，待消解杯中的溶液开始冒泡时，将其取下，并用0.5%硝酸稀释定容至25mL。

(1)首先采用自编码网络，训练从输入层到H1层的参数，训练完毕后，去除解码层，只留下从输入层到隐藏层的编码阶段；

(2)接着训练从H1到H2的参数，把无标签数据的H1层神经元的输出值作为H2层的输入，然后再进行自编码训练，训练完毕后，再去除H2层的解码层；

(3)对所有层重复(1)和(2)，即移除前面自编码器的输出层，用另一个自编码器代替，再用反向传播进行训练，直到栈式自编码器的层数达到k。

本文所用栈式自编码器结构如图4所示。编码器部分神经元采用递减式结构，减少了重要信息的丢失；输出层的维度为49；在解码器部分，各层神经元数与解码器对称，使用式(5)作为映射函数。

图4 栈式自编码器

1.3 卷积自编码器

含有卷积操作层(Convolutional layers)的自编码器称为卷积自编码器。卷积层含有一系列滤波器，在特征图上按照一定的步长滑动，将卷积核参数与像素值对应相乘后相加输出。卷积层作用于图像的局部区域进而获得图像的局部特征，多层卷积层的应用，可以扩大这个局部区域的范围，使提取到的特征更具备空间特性，因此卷积操作更适合用于图像领域[15]。

本文使用的卷积自编码器结构如图5所示。在编码器部分，卷积层数量为3，每层卷积核数量递增，卷积核的大小为3×3，步长为3；在输出层与卷积层之间有一个全连接层作为过渡；输出层维度为49；在解码器部分有与编码器部分对称的全连接层和反卷积层，使用式(5)作为映射函数。

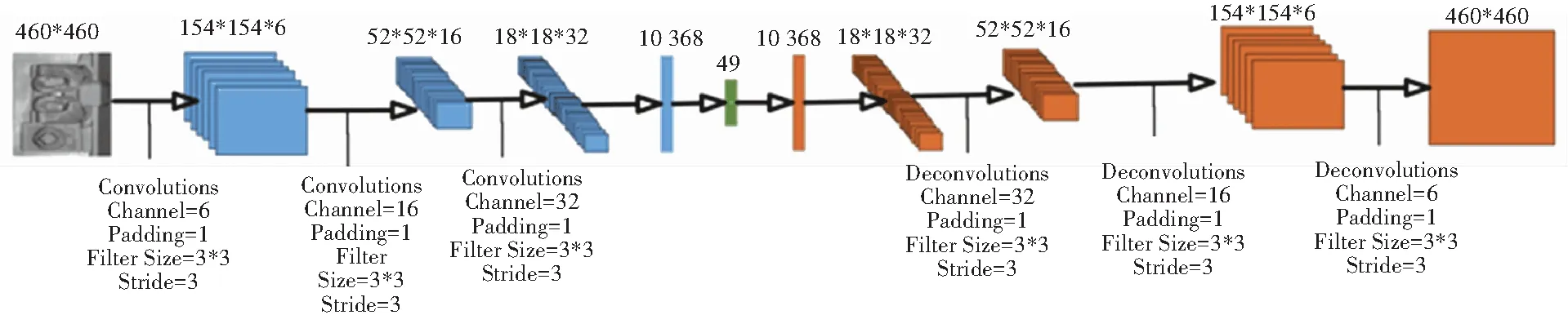
图5 卷积自编码器

2 余弦相似度和多数投票法

扣件图像经自编码器提取的特征都为49维的高维特征，本文使用余弦相似度作为度量这些高维特征之间相似度的尺度。余弦相似度是用空间中两个向量的夹角来判断这两个向量的相似程度，两个向量夹角越大，距离越远，最大距离就是两个向量夹角180°；夹角越小，距离越近，最小距离就是两个向量夹角0°，完全重合。假设有A、B两个n维向量，余弦相似度用式(6)求解。

(6)

其中，Ai和Bi代表向量的第i维的值。使用3种自编码器对扣件图像特征进行编码，并通过余弦相似度确定扣件状态，当3种方法识别的扣件状态不一致时，使用多数投票法确定结果。假设扣件的正常状态用1表示，异常状态用0表示，其真值见表1。

表1 投票法真值表

3 实验结果与分析

本文实验涉及的软硬件平台及版本信息见表2。

表2 实验软硬件平台及版本信息

以下实验都基于相同的软硬件条件。本文将扣件分为正常状态和异常状态两类，如图6所示。异常状态扣件包括断裂、弹出等情况。数据集中图像共600张，其中正常状态扣件430张，异常状态扣件170张。随机选取260张正常图像作为训练集，340张作为测试集。测试集中正常状态扣件170张，异常状态扣件170张。

图6 扣件状态

本文用向量余弦值作为扣件状态的判定标准。在训练集中，任意选取一个图像作为参照，经过自编码器得到的特征T定义为基向量，训练集中其余图像经过自编码器得到的向量与基向量求余弦值，该余弦值为两张图像的相似度，范围为-1～1，相似度越接近1，向量代表的图像与基向量越相关。在不同算法中特征向量的提取不尽相同，对3个自编码器进行上述操作，得到的相似度最小值见表3。

表3 各算法的最小相似度

本文将测试图像的相似度阈值设置为训练集中相似度的最小值，即测试图像的自编码向量在相似度最小值和1之间时扣件为正样本，否则测试图像中的扣件为负样本。为进一步提高算法的正确率，本文使用投票法对3种算法给出的结果使用多数投票法进行投票。各个算法实验结果见表4。

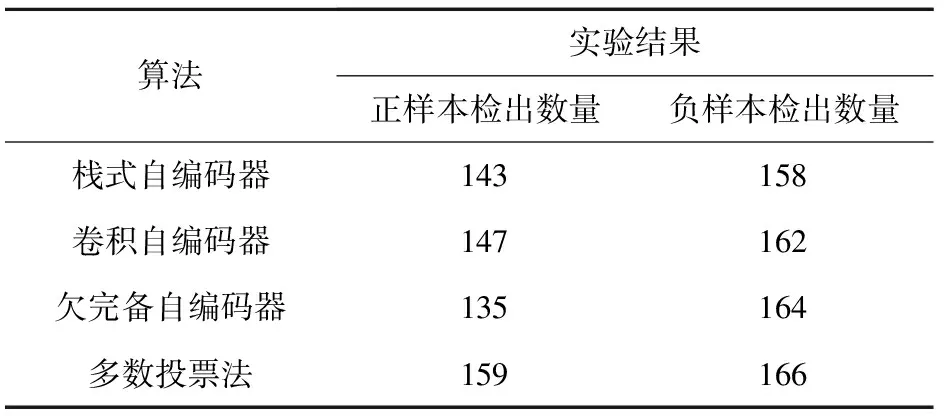
表4 自编码器实验结果

实验证明，自编码器可以有效地提取扣件特征，将扣件图像信息映射到高维空间中，利用特征之间的相似度实现了在只训练正样本的情况下检测扣件状态。从负样本的检出数量来看，因为卷积自编码器的卷积操作能更好地提取到扣件的空间特征，使得3种自编码器中，卷积自编码器表现最好。使用多数投票法后，正样本的检出数量和负样本的检出数量都有所增加。

代先星使用VGG深度学习网络对扣件进行分类[8]，李永波使用HOG特征提取与SVM分类器结合方式检测扣件[10]，这两种算法的指标在各自的数据集中都较为优秀，为证明本文算法的优越性，在相同的软硬件条件和数据集下将本文方法与以上两种算法对比，并使用总体精度(Overall Accuracy，OA)、精确率(Precision)、虚警率(False alarm，FPR)和漏警率(Missing alarm，FNR)评估扣件状态检测算法，式(7)～(10)。

(7)

(8)

(9)

(10)

其中，TP表示算法被正确分类的个数;N代表所有测试集的数量;NTP表示数据集中正样本数量;NFP表示负样本被检测为正样本的数量;NTN表示数据集中负样本的数量;NFN表示正样本被检测为负样本的数量。

因为扣件状态的检测关乎铁路安全，所以在保证整体精度的情况下，虚警率越低越好，算法分类实验结果见表5。由实验数据可知，传统的机器学习在没有负样本时，整体表现较差，不能达到扣件状态检测的效果；基于深度学习的VGG网络只通过学习正样本数据，总体精度不够，虚警率过高，不适用于扣件检测这种负样本较少的情况；本文方法不管是在总体精度还是虚警率方面比前两种方法都大有改观，综合各个评价指标，本文提出的扣件检测算法最好，实现了零样本检测铁路扣件状态。

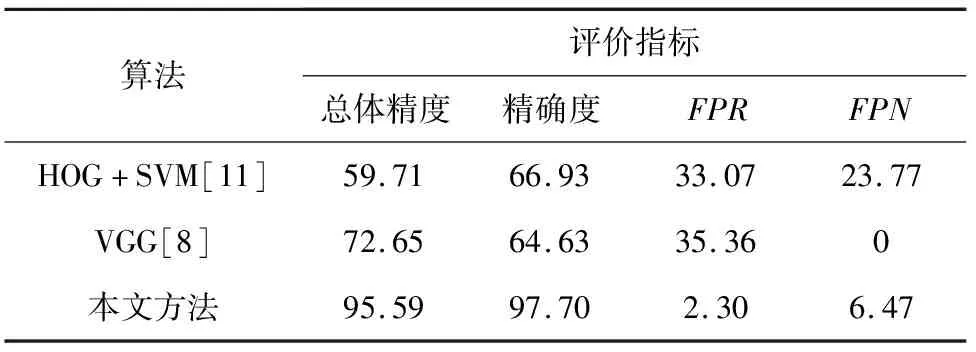
表5 算法分类实验结果

4 结束语

本文提出了一种基于卷积自编码器的零样本扣件检测方法，首先通过欠完备自编码器、栈式自编码器和卷积自编码器分别对扣件提取特征，再通过特征与基向量的相似度判定扣件的状态，最后通过多数投票法最终确定扣件状态，为铁路扣件检测提供了一种新的解决思路。本文算法在测试集中的整体精度为95.59%，精确度为97.70%，FPR为2.30%，FPN为6.47%，比传统方法和深度学习方法在评价指标方面有所提升，本文方法解决了利用机器视觉算法检测扣件状态时数据集不均衡的问题。