基于灰度拉伸和遗传算法的焊缝图像二值化算法

黄 静，蒋泽宁

(浙江理工大学 信息学院，杭州 310018)

0 引 言

随着计算机视觉技术的蓬勃发展，基于视觉传感的自动化焊接技术日渐成为智能焊接领域的一个研究热点。焊缝图像处理是焊缝自动跟踪的一个较为重要的环节，其主要任务是对视觉传感器所采集的图像信息进行加工处理, 以提取焊缝图像的特征信息，而图像二值化在此过程中起着关键性的作用。二值化阈值的选取至关重要，过高或者过低都会对焊缝边缘提取任务造成不利的影响。

图像二值化过程的主要任务就是把焊缝的灰度图像变成取值为0和1的二值图像[1]。对一幅焊缝灰度图像进行二值化操作时，首先要选取合适阈值，把所有高于阈值灰度的像素点替换成1，所有低于阈值的像素点替换成0。但实际操作中，由于不同图像的灰度基值不同，同一幅图像中各部分的明暗程度不同，因此阈值的设定很困难。对图像进行二值化处理，一方面对图像信息进行了压缩，保留了焊缝的主要信息，节约了存储空间，有利于计算机存储和处理；另一方面还可以去除大量的粘连，为焊缝特征的提取和匹配做准备。

1 二值化研究现状

国内学者对经典的Otsu算法进行了研究改进，申俊琦等通过最小二乘法建立图像阈值与焊缝激光带区域灰度平均值的直线回归方程，从而得到焊缝图像二值化处理的最佳阈值[2]；王兴东等提出了一种基于区域优化的等厚对接焊缝图像二值化方法[3]；齐继阳等提出了一种新的改进的Otsu法，在考虑类间方差和类内方差对图像分割效果影响的基础上，用方差信息代替均值信息，构建了焊接图像分割阈值算法[4]；徐建东等提出了基于最小二乘法拟合的Otsu快速图像分割法等[5]。

传统的Otsu阈值化算法对信噪比较低的图像分割效果不理想，本文提出将传统Otsu方法与遗传算法相结合，通过灰度拉伸增大背景与前景之间的灰度值分布，结合遗传算法，通过编码、选择、交叉、变异等操作对传统的类间方差法进行优化，并将该方法试验于焊缝图像。实际焊缝图像试验结果证明了该方法的有效性，可以更加准确地提取出适合焊缝图像的二值化阈值，更利于后续的图像处理操作。

2 改进的二值化方案

针对灰度化后背景灰度值与前景相近的问题，利用遗传算法选择两个灰度拉伸因子，增大背景与前景的区分度[6]。为了获得可靠的二值化阈值，综合考虑类间方差与类内方差。

2.1 灰度拉伸

灰度拉伸是一种改变图像对比度的方法，通过某种映射关系，将原图像中的灰度值映射为另一个灰度值，从而达到拉伸或压缩整个图像灰度分布的目的。当环境光照强度较大时，通过摄像头拍摄的焊缝图像灰度化后有相当多的背景灰度值与前景相似，使二值化阈值变得难以选取。通过灰度拉伸，可以增大背景与前景之间的灰度值分布[7]。灰度化的焊缝图像按灰度强度可以分为3个部分，高值的焊缝区域，有较大差异的低值背景区域，接近焊缝灰度值的中值背景区域。因此，灰度拉伸的关键在于中值灰度区域。根据区域划分的特点，本文选用了sigmoid函数作为灰度变换函数。sigmoid函数的基本表达如式(1)：

(1)

从公式(1)可以看出sigmoid是一个单调递增函数，值分布在0～1之间，函数图像如图1所示。

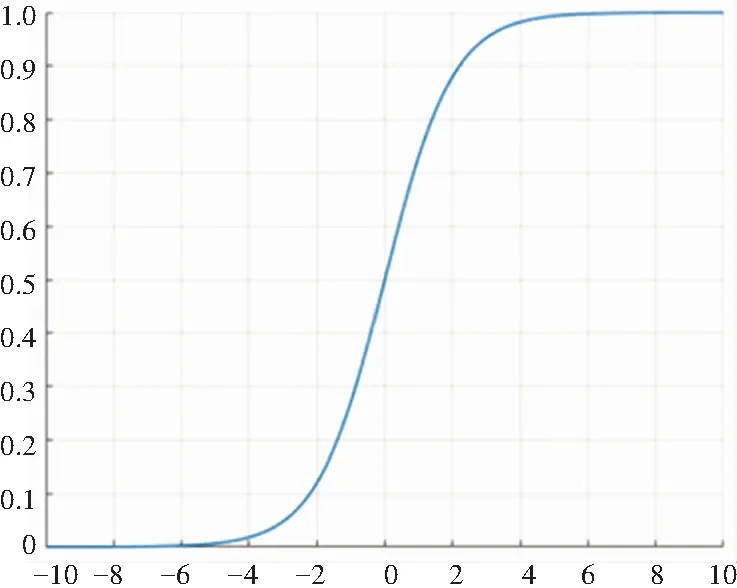
图1 sigmoid函数图像

可以发现，sigmoid函数在变量为0附近区域值变化非常剧烈，区域外函数值变化平稳，接近常数。sigmoid函数分布符合焊缝灰度拉伸的基本要求，本文将灰度图像的最小值与最大值先映射到-10～10区间，再通过sigmoid函数拉升到0～255。初次映射公式(2)如下：

(2)

其中，maxP、minP分别为最大灰度值和最小灰度值，i为输入的灰度值。

通过上述方式进行灰度拉伸还存在一个问题，如果x(i)集中在0的单侧(左侧或右侧)，会造成拉伸后的灰度值大概率被归结于前景或背景，影响阈值选取。因此，引入拉伸因子C调节sigmoid函数在变量值0附近的变化率，将变量x与C相乘，根据x与0的大小关系，选择不同的C值。拉伸因子不同取值下，sigmoid函数图像如图2所示。

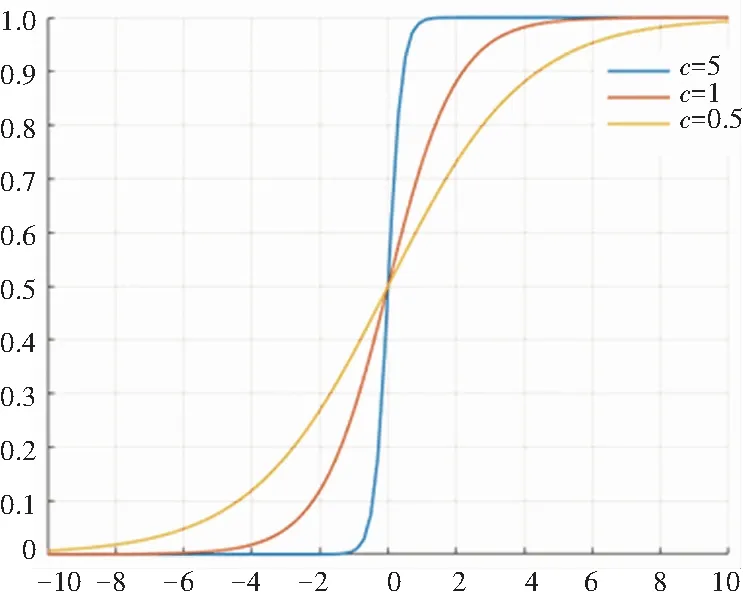
图2 不同拉伸因子取值下的sigmoid函数图像

从图2可以发现，随着C值的变大，sigmoid函数图像变得更加陡峭，这意味着调节拉伸因子，可以改变原灰度区间的拉伸变化率。本文根据公式(2)确定x的值后，对x>0与x<0分别选择不同的拉伸因子。灰度拉伸的表达如式(3)：

(3)

2.2 类间方差与类内方差

2.2.1 类间方差

类间方差也称作大津法(OTSU)，由日本学者大津提出。大津法的原理非常简单，但效果优异，在数字图像处理领域得到广泛应用。根据图像的灰度分布特性，大津法将图像分为背景和前景两部分，利用方差度量图像灰度分布的均匀性[8]。背景与前景之间的方差越大，表明两者之间的差异程度越高，发生错分的概率越小。类间方差的求解利用了灰度直方图，假定分割阈值为Th，将小于该值的灰度划分为背景，大于的则划分为前景，每个灰度级占整幅图像的比例为式(4)：

(4)

其中，hist(i)表示灰度为i的像素值个数。

由此可以计算出前景与背景的占比及均值，如式(5)～(8)：

(5)

(6)

(7)

(8)

根据类间方差的定义，可以得到公式(9)：

(9)

根据公式(9)，遍历0～255个灰度级，就能够得出最大的类间方差，此时的分割阈值即为所求结果。

2.2.2 类内方差

最大类间方差旨在尽可能的分离背景与前景，评判标准仅考虑目标与背景的距离，但是在灰度值相近区域可能发生灰度值误判的情况[9]。为了减少这种情况的发生，引入类内方差。类内方差关注的是目标的内聚性，如果灰度值与目标的中心距离较近，则有更大的概率属于该类，这意味着目标有着较小的类内方差。定义类内方差的表达如式(10)：

(10)

至此，综合考虑类间方差与类内方差，可以得到阈值分割的评估函数(11)：

(11)

该评估函数与类间方差成正比，类内方差成反比，符合上述分析。

2.3 遗传算法

达尔文的生物进化论以及其遗传规律指出生物的进化是一个依照群体遗传与自然选择机制结合的过程。其中有利的基因将遗传给下一代，而不利的基因将在此后的更替中逐渐消亡。遗传算法就是模拟生物进化过程中自然选择和自然遗传机制的一种广度优化搜索算法[10-12]。

利用遗传算法找出两个拉伸因子以及分割阈值的实现过程：

(1)编码。由于遗传算法不能直接处理解空间的解数据，染色体必须采用二进制字符串编码，图像灰度值的取值范围在0～255之间，所以采用00 000 000～11 111 111八位二进制代码代表图像灰度值。灰度拉伸因子C值的取值范围在0～32之间，根据变量x的正负分成两种情况，所以采用十位二进制代码表示，其中高5位为变量x>0条件下的拉伸因子C1，低5位为变量x<0条件下的拉伸因子C2。将灰度因子和灰度值结合，共计18位二进制代码来表示，前5位、中5位和后9位分别表示拉伸因子C1、拉伸因子C2和图像灰度值。

(2)初始化群体。在[1，32]之间随机生成一个整数C1，在[1，C1]之间随机生成一个整数C2，在[0，255]之间随机生成一个整数Thres，重复上述步骤n次，生成n组(C1，C2，Thres)，并将其以二进制的形式编码成18为二进制码，初始化群体。

(3)评价。评估种群中个体适应度，首先根据变量x的正负，通过灰度因子C1和C2进行灰度拉伸；将sigmoid拉伸后的灰度值进行类间方差的计算，得到种群中的个体适应度，对种群适应度求和；根据方差找出最优个体，进行个体适应度概率的计算。

(4)选择。本文采用轮盘赌选择(Roulette Wheel Selection)，每个个体进入下一代的概率等于其适应度值与整个种群中个体适应度和的比例。

(5)交叉。在[0.00，0.999]之间取任一随机数，与初始设定的交叉概率CP比较之后进行重组运算，产生两个新的个体，新的个体既保留了双亲的部分基因，同时也引进了新的基因。

(6)变异。在[0.00，0.999]之间取任一随机数，与初始设定的变异概率MP比较，符合变异条件的个体在相应的进制位上进行二进制取反操作以实现变异，从而形成新的个体。

(7)循环。每一次进化都会更优，因此理论上进化的次数越多越好，但在实际应用中往往会在结果精确度和执行效率之间寻找一个平衡点，设定循环演化的迭代次数NG。

(8)结果处理。将最后一代群体之适应度最大的个体作为遗传算法所寻求的最优结果，并将其反编码成[0，255]之间的灰度值即为最佳阈值。

3 实验及结果分析

3.1 实验环境搭建

实验整体环境如图3所示。选择了ROSEEK公司提供的Woodpecker1系列CCD彩色工业相机，该相机拥有4 GB的内存，能够在[-40 ℃，80 ℃]条件下正常启动并长期稳定工作，12 w的最大功耗，390 g的重量，满足实验需求；选择一字线激光器作为激光源，其波长是635 nm，优点是能获得亮度大小适合、光源相干性能较好、不存在闪烁的一字线光带，可以在焊接处进行较为均匀的照明，形成高质量的焊缝成像图像；将工业相机摆放在水平平稳的支架上，连接到PC上以控制相机对焊缝图像进行采集和后续的处理。

图3 实验整体环境图

为验证本文方法的有效性和实用性，对采集的焊缝图像做了大量的试验。本实验是在Microsoft Visual Studio 2019平台上开发，图像处理算法主要是以C++代码的形式及调用OpenCV函数实现的。遗传算法中设定种群大小n=20，终止迭代次数NG=20，交叉概率CP=0.9，变异概率MP=0.1，拉伸因子C1_MAX=32。

3.2 实验结果

首先对如图4所示的原始焊缝图像应用传统的Otsu算法进行二值化，得到传统Otsu阈值化后的结果如图5所示，可以明显看出存在反光噪声，焊缝光带边界不光滑，定位不够精确，目标与背景存在混淆等问题。传统的Otsu大津法对图像噪声较为敏感，只能对单一目标分割，当目标和背景大小比例悬殊、类间方差函数就可能会呈现双峰或者多峰，阈值分割效果不太理想。

图4 原始焊缝图像

图5 Otsu阈值化后的图像

为了应对实时的焊接要求，应有效滤除噪声、准确且高效地提取焊缝光带，故本文将传统Otsu方法与遗传算法相结合，通过灰度拉伸增大背景与前景之间的灰度值分布，结合遗传算法，通过编码、选择、交叉、变异等操作对传统的类间方差法进行了优化，并将该方法应用于焊缝图像。实际焊缝图像试验结果如图6所示，证明了该方法的有效性，可以更加准确地提取出适合焊缝图像的二值化阈值。

图6 改进后的阈值化图像

4 结束语

传统的Otsu大津法对图像噪声较为敏感，只能针对单一目标分割。当目标和背景大小比例悬殊、类间方差函数就可能会呈现双峰或者多峰，阈值分割效果不太理想。本文将传统Otsu方法与遗传算法相结合，通过灰度拉伸增大背景与前景之间的灰度值分布，结合遗传算法，通过编码、选择、交叉、变异等操作对传统的类间方差法进行了优化，并将该方法应用于焊缝图像。实际焊缝图像试验结果证明了该方法的有效性，可以更加准确地提取出适合焊缝图像的二值化阈值，更利于后续的图像处理操作。