基于对称百分误差的线性回归与印染工业应用

宋丛威，张晓明

(北京雁栖湖应用数学研究院, 北京 101408)

0 引 言

目前印染工业面临的问题，是根据已知的颜色，给出染料浓度配比，使得布料染出所需颜色[1]。文献[1]中已经建立了一个高效的线性模型用于预测染料浓度，本文则讨论另一种预测浓度的方案。工人通常会在正式染色前，对样品进行试验性的染色，得到一组浓度配比。这本身也是目前印染业标准生产流程的环节。理想情况下，样品试验得到的是正式染色的浓度配比。但在实际效果上却总是存在一定的误差。为了利用样品试验数据来预测正式染色时的染料浓度配比，提出了线性模型[2-3]：

其中，x、y分别是样品浓度配比和正式染色的浓度配比。

注意：x是向量，代表样品试验浓度配比，而y是数量，代表正式染色的浓度配比的一个分量。即使y是向量，也假定各分量是独立的，则分别研究每个分量即可。

为了便于理论分析,把所有参数整合成一个向量θ=(a,b)，并把线性模型表示为[4]：

(1)

其中，Cφ(x)表示由x决定的一组基。在本文中由x的分量和1构成。考虑到下述对数线性模型：

(2)

相当于对y做对数化预处理。由于x、y有相同的物理意义，x也会做对数化预处理。

设θ为p维向量，对于N个样本，则有：

(3)

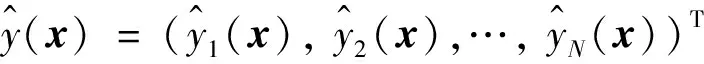
本文对相对误差做一些改良。此时，最小二乘法的代数方法不再适用，需用梯度下降法(GD)进行优化。这就是本文要解决的技术问题。最后的数值实验说明，在该误差下，本文方法优于普通的线性回归。

1 百分误差与损失函数

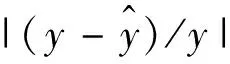
1.1 矩阵分析

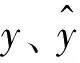
(4)

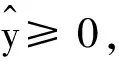
(5)

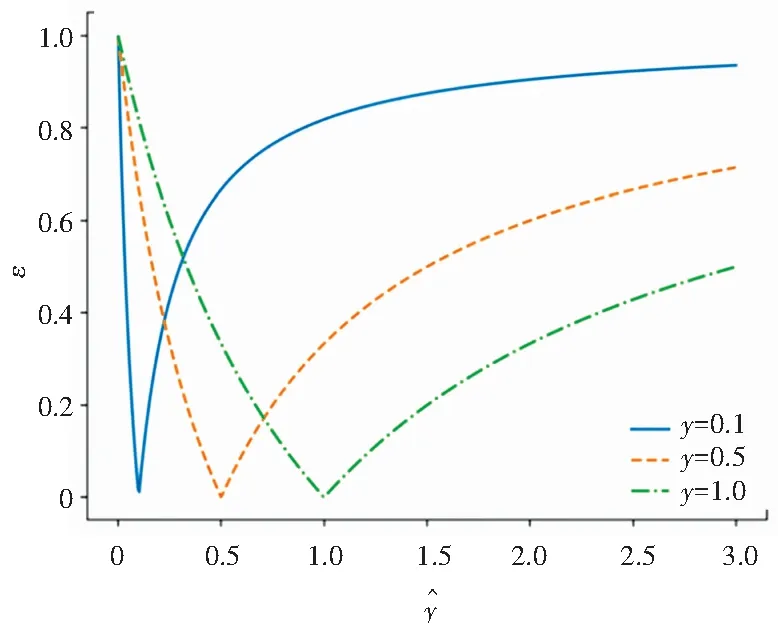
图1 不同y值产生的误差绝对值

如此定义相对误差的好处，就是对异常值不敏感。不对误差取绝对值，是为了更准确地反映误差的分布。

数值计算中，小数除法会导致溢出，必要时改造为：

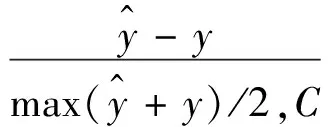
其中，C>0是一个合理的常数，在程序实现时考虑这一点。

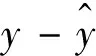
对于多维情形y=(y(1),…,y(n))，对每个分量计算误差或直接用其2范数平方根取代：

(6)

注：本文用下指标给样本编号，用上指标表示分量。

1.2 损失函数

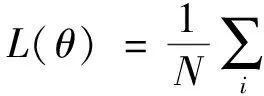
(7)

这个损失函数被称为(对称)均方百分误差。

用代数方法可以求解绝对误差下的损失函数最小化问题，但不能求解损失函数(7)的最小化问题。相反，本文采用一种常用的梯度下降法(GD)——Adam算法[11-12]，预测可以得到比最小二乘法更好的解。

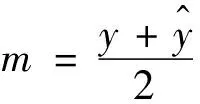
(8)

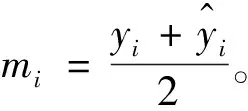
注：导数中可能出现小数的三次方除法，故在程序设计时需考虑溢出和梯度值异常。

式中省略了归一化参数，C大致为方差的倒数，这个值基本决定了置信度。该分布形状类似于逆Gamma分布，如图2所示(因为归一化因素的存在，y轴不必显示刻度)。令相对误差ε服从“紧支撑的正态分布”ε～exp{-Cε2},-1≤ε≤ 1，而绝对误差变成了偏态的。

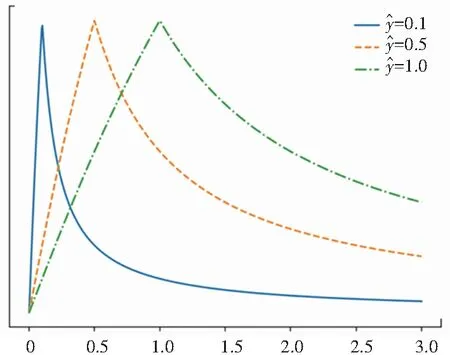
图2 不同估值下y的分布

最后，损失函数的多维形式为：

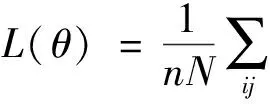
就本文的线性模型而言，多维输出不是本质的。因为每个分量均独立，所以只需单独对每个分量应用GD，然后对其对应的损失函数值求平均即可。

1.3 损失函数其它形式

损失函数：

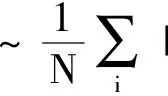
(9)

称为(对称)平均绝对值百分误差[13]。此时，梯度为(已省略次要系数)：

其中,符号函数：

等价于，假定y服从下述分布的极大似然估计。

通常可以考虑：

(10)

不过对GD而言，p=2依然是首选。

2 算法与实验

本文算法利用Python3.8实现, 运行于MacOS10.15上，程序设计遵从scikit-learn的API设计规范[14-15]。已在Gitee上公开了所用数据、源代码和运行结果, 网址为https://gitee.com/williamzjc/relinear。

2.1 算法

在此，虽然最小二乘法不再适用，但可以用来初始化参数。对于可微性较好的相对误差，采用梯度下降法；对于可微性较差的相对误差，采用遗传算法等智能算法。

算法设计采用Adam算法优化误差函数。基本处理过程概括如下：

(1)输入x、y。

(2)可用最小二乘法初始化θ或随机初始化。

(3)根据式(8)计算梯度，并用Adam算法优化L(θ)，得到最终的θ。

(4)预测测试数据。本算法还具有增量学习功能。学习未来产生的数据时，可以从当前存储的θ开始迭代，无需初始化。

2.2 实验

实验数据来自绍兴的一家印染工厂。输入变量X是样品在小缸中进行实验的染料浓度，输出变量Y是正式染色时的染料浓度。两者维度为3，因此包含3个线性模型，每个模型有4个参数，总共134条数据。

数据被随机分成训练数据(80%)和测试数据(20%)。损失函数选用式(7)来计算。将本文算法和多种常用的线性模型相关算法进行比较，测试重复进行50次，产生50份实验数据。最后取这50份实验数据的中位数作为最终的结果，并保留4位有效数字，实验结果见表1。

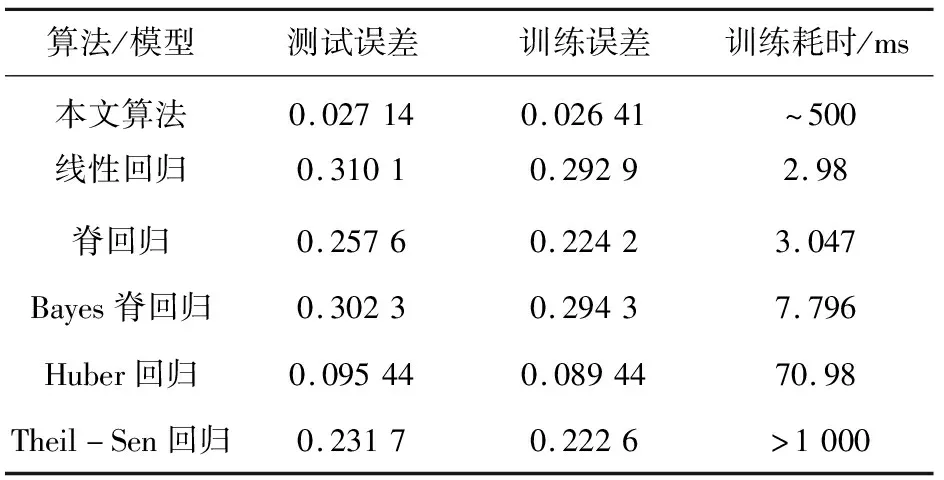
表1 数值实验报告

对数线性模型测试结果见表2。

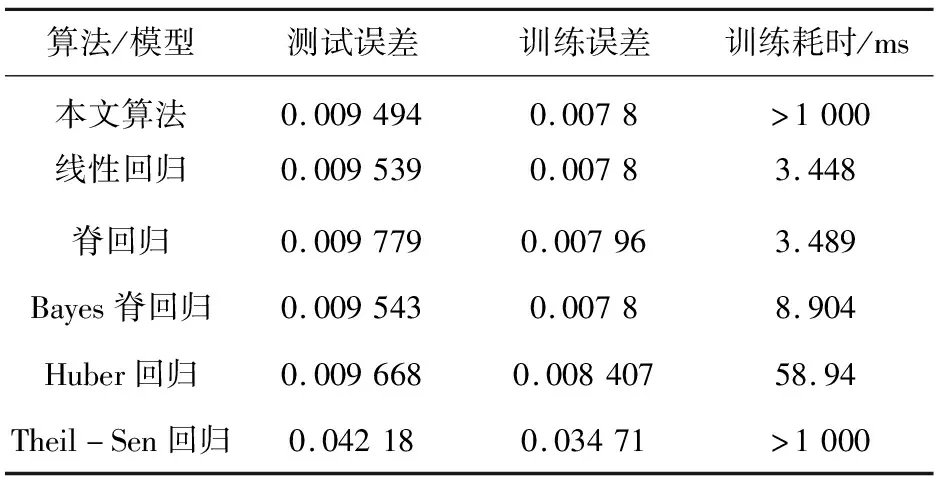
表2 对数线性模型的数值实验报告

实验验证了本文算法的有效性。在线性模型中，其表现显著超越所有算法。但在对数化模型中，所有算法整体上表现相当，其中本文算法的训练误差稍优于其它算法。就本问题而言，对数化处理似乎非常有效，以至于一定程度上掩盖了本文算法的作用。为了降低误差，设置较高的迭代次数，同时也增加了训练时间。

3 结束语

在工业生产中，损失函数通常有实际意义，比如y值越小样本权重越大。本文最终选择式(4)和式(7)作为误差函数和损失函数。对称百分误差导出的偏态分布一定程度上接近真实数据的分布情况。

本文算法的核心是通过GD优化误差函数，通过实验充分证实了本文算法的有效性，可应用于工业领域。在精度方面显著高于其它算法，但是效率较低，有待提高。

未来工作主要寻找并研究其它可行的损失函数。损失函数与误差的分布是联系在一起的。因此，构造合理的误差分布也将是未来的任务之一。