车用载具装备有限元网格剖分定制化策略研究
2021-11-12林鉴岳董焱章程文明王辉
林鉴岳,董焱章,*,程文明,王辉
车用载具装备有限元网格剖分定制化策略研究
林鉴岳1,董焱章1,2*,程文明2,王辉2
(1.湖北汽车工业学院 汽车动力传动与电子控制湖北省重点实验室,湖北 十堰 442002;2.湖北迪迈威智能装备有限公司,湖北 十堰 442002)
为解决非标类机械结构仿真分析和优化设计中有限元网格尺寸选择问题,文章提出一种有限元网格剖分的定制化策略通用流程,即在结构有限元网格收敛性得以保证的基础上,综合考量有限元收敛精度和计算时间成本的双重影响,针对结构仿真中不同的分析和设计需求,提供相应的有限元网格剖分策略。算例结果表明:对于车用载具装备,采用计算时间成本最小的网格剖分方案可大幅缩减结构概念设计阶段(拓扑优化设计)周期;采用收敛精度最高的网格剖分方案可有效提高结构性能评价(单次重分析)可信度;采用折中的网格剖分方案则可较好地平衡详细设计阶段(尺寸优化设计)的计算时间成本和收敛精度要求。
车用载具装备;网格剖分;收敛性分析;定制化策略
前言
车用载具装备是在早期SQ系列铁道运输平车基础上,为满足汽车行业生产制造需求专门开发设计出来的一种运输工作平台,其主要功能为承载、运输相关器件物料等,其具有承载能力强、货损少和效率高等优势,运输平车经过相应修改亦可应用在特种运输和危险救援等领域[1-7]。车用载具装备设计阶段需要对其结构进行力学性能分析,通常是借助有限元软件进行几何建模和求解,由于车用载具装备属于非标类设计产品,其不同的产品结构间差异较大,故有限元分析中的网格尺寸如何选择变得棘手,网格尺寸的恰当选择通常是借助网格收敛性分析来实施的[8-9]。
网格收敛性分析主要存在两类方法:网格自适应剖分法和整体细化法。其中网格自适应剖分法是调整有限元模型几何尖锐或者关键区域的单元尺寸进而实现局部网格加密,在减少计算时间的同时又保证了计算精度[10]。此外,基于算法设计的网格自适应剖分法研究主要聚焦在基于标记策略和后验误差估计的收敛性分析中[11-17]。通常来讲,网格自适应剖分法的求解精度不如整体细化法,研究者也对整体细化法进行了积极探索,力求最大程度地减少分析时间,如胡季等[18]基于Ansys采用APDL命令流进行了二次开发,有效缩短了有限元建模的时间;Patil等[19]基于开源求解器CodeAster搭建了自动化网格细化求解平台,同样减少了重复繁琐的操作步骤。
尽管如此,对网格收敛性分析的研究,收敛精度和计算时间往往无法兼得,且对于不同的工程实际需求,比如性能评价分析和性能优化设计,对于收敛精度和计算时间的要求不尽相同,此时有必要针对不同的工程需求建立不同的有限元网格剖分策略。本文首先提出了一套基于整体网格细化的有限元网格剖分定制化策略通用流程,然后以车用载具装备为算例,建立其多方案有限元模型,进而完成其网格收敛性分析,然后综合评价收敛精度不同的多套有限元模型,最后确定满足不同工程需求的车用载具装备有限元网格剖分定制化策略。
1 有限元网格剖分定制化策略研究通用流程
非标类机械结构的几何模型导入有限元程序经过初始建模后,初始给定一个有限元网格尺寸(单元尺寸)0,然后将0对半缩减次后,借助网格自动剖分工具获得1、2、…、S-1、S等+1套不同单元尺寸下的有限元网格,接着进行材料赋值、载荷施加和边界条件设置等操作,最终建立+1套不同单元尺寸下的有限元模型。针对上述+1套有限元模型,实施仿真计算分析,并从其分析结果中随机选择几个位置,判断所选位置的节点应力值是否收敛,若结果收敛则针对不同工程需求,按照收敛精度和计算时间的差异制定相应的有限元网格剖分策略;若结果不收敛则重新调整单元尺寸0,重复上述步骤,整个通用流程如图1所示。
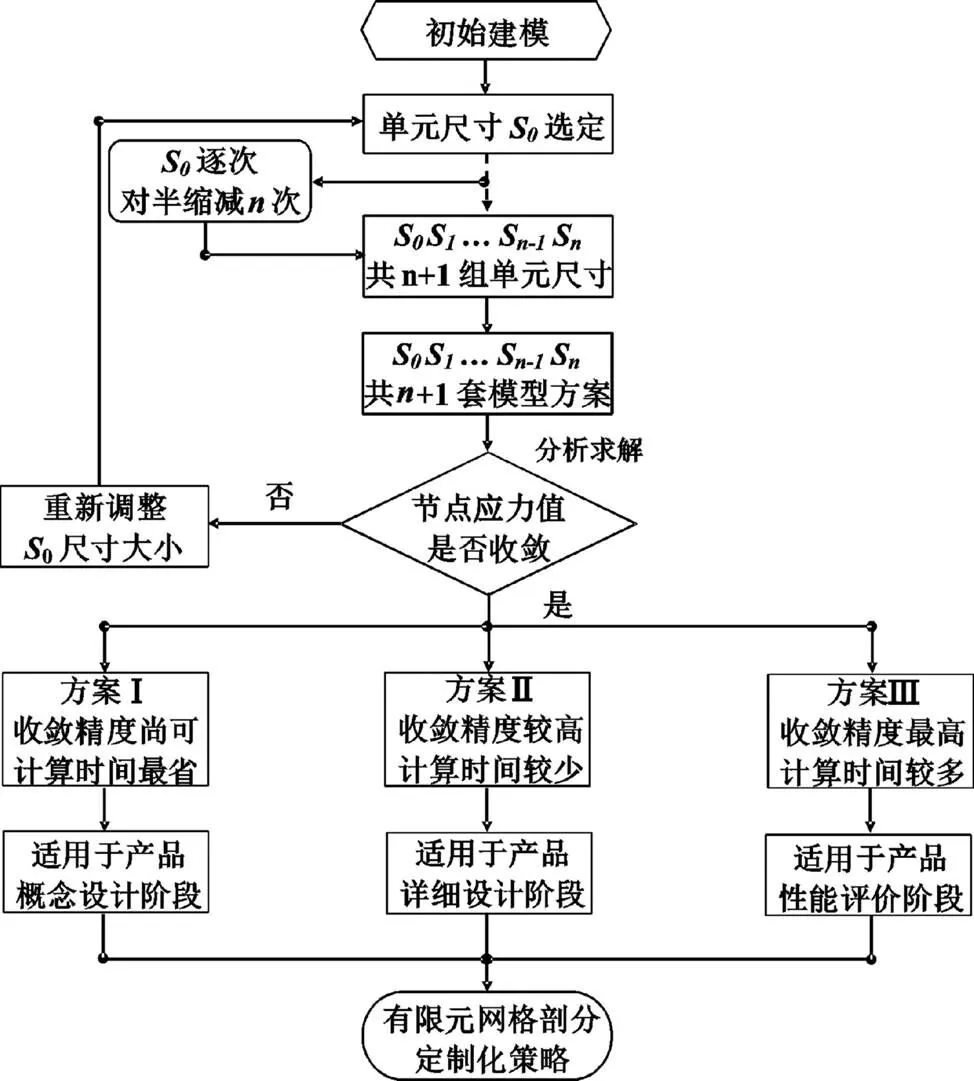
图1 有限元网格剖分定制化策略通用流程图
2 有限元网格剖分定制化策略算例:车用载具装备
2.1 车用载具装备有限元模型建立
针对某型车用载具装备,依次选用20 mm、10 mm、5 mm、2.5 mm和1.25 mm等尺寸的壳单元对其结构进行整体网格剖分,接着实施焊接和螺栓连接[20-21]、材料赋予(Q235A)、载荷施加和边界条件的设置,最终建立五套不同单元尺寸的车用载具装备有限元模型。
其中载荷施加时采用质量单元和载荷传递单元结合来实现载重的模拟。此外,边界条件通过约束车用载具装备的下方支撑处的所有自由度来模拟其工况。
2.2 车用载具装备有限元网格收敛性分析
对五套不同单元尺寸的车用载具装备有限元模型进行仿真分析,从其应力云图中随机选择Ⅰ、Ⅱ、Ⅲ、Ⅳ等四处(具体位置如图2所示)节点应力值进行对比分析,进而判断结构有限元的网格收敛性情况。
为便于观察五套不同单元尺寸的有限元模型分析获得的节点应力值变化趋势,横坐标的单元尺寸使用其对数值(log20、log10、log5、log2.5、log1.25),纵坐标为随机选择四处位置的节点应力值,从而得到了相应位置处节点应力值随单元尺寸的变化趋势,如图3所示。从图中结果可以发现:位置Ⅰ、Ⅱ、Ⅲ等三处节点应力值随着单元尺寸的缩减而趋增,位置Ⅳ的节点应力值则随着单元尺寸的缩减而趋减;尽管如此,除了前两个单元尺寸(20 mm和10 mm),后三个单元尺寸(5 mm、2.5 mm和1.25 mm)下四处位置(Ⅰ、Ⅱ、Ⅲ、Ⅳ)的节点应力值呈现出比较明显的收敛趋势。
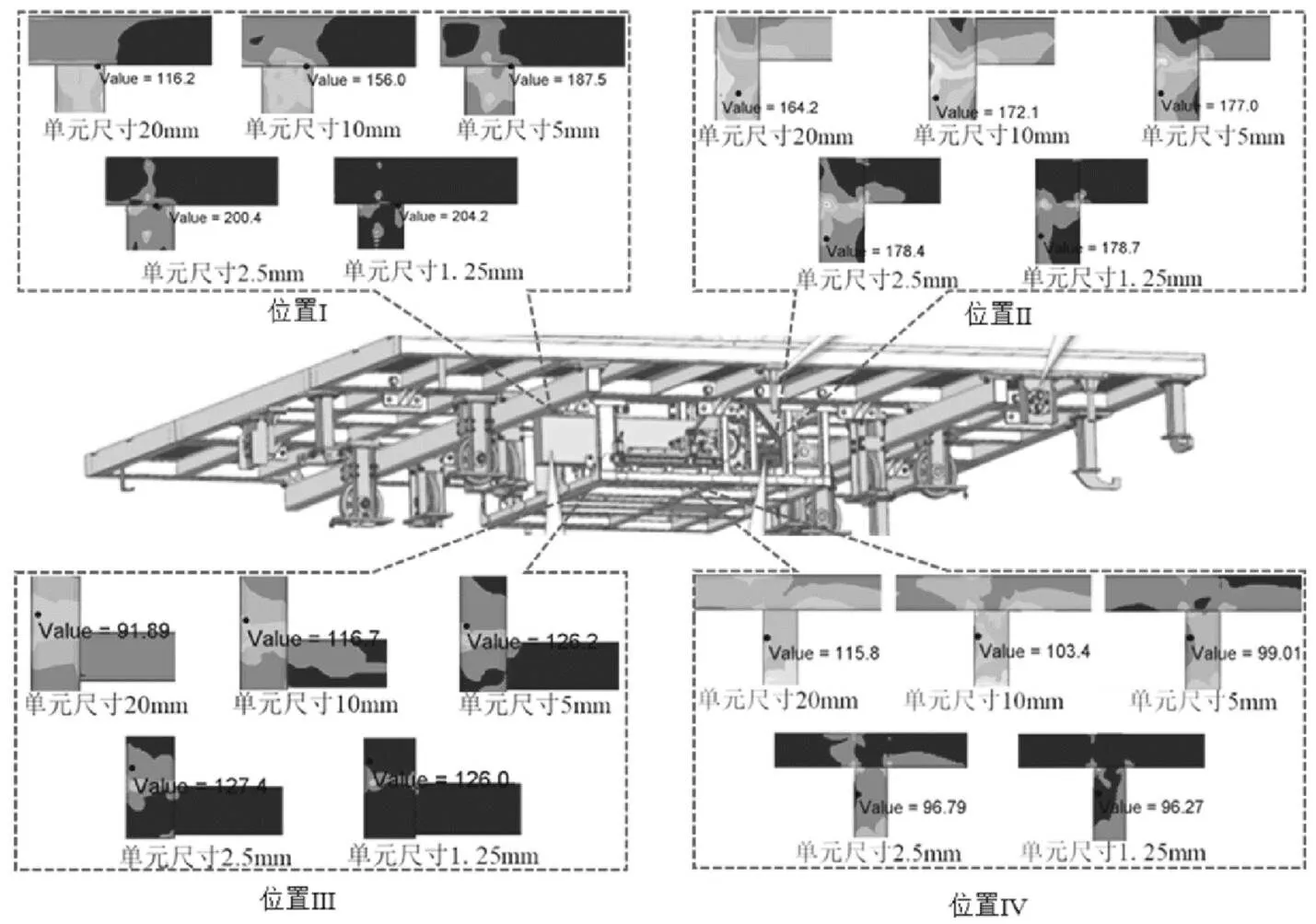
图2 不同单元尺寸下随机选择四处位置的局部应力云图

图3 随机选择四处位置节点应力值随单元尺寸的变化趋势
进一步地分析,不同单元尺寸下随机选择四处位置(Ⅰ、Ⅱ、Ⅲ、Ⅳ)的节点应力值具体变化情况如表1所示。
由表1可知,与图3不同单元尺寸下随机选择四处位置的节点应力值变化趋势相对应:单元尺寸20 mm下,位置(Ⅰ、Ⅲ、Ⅳ)的节点应力幅值变化超过10%,位置(Ⅱ)的节点应力幅值变化也接近5%,故单元尺寸20 mm属于网格未收敛情形;单元尺寸10 mm下,位置(Ⅰ、Ⅲ)的节点应力幅值变化超过5%,位置(Ⅳ)的节点应力幅值变化也接近5%,故单元尺寸10 mm属于网格未收敛情形;单元尺寸5 mm下,除了位置(Ⅰ)的节点应力幅值变化略高于5%外,位置(Ⅱ、Ⅲ、Ⅳ)的节点应力幅值变化均低于5%,故单元尺寸5 mm属于网格收敛度尚可情形;单元尺寸2.5 mm下,位置(Ⅰ、Ⅱ、Ⅲ、Ⅳ)的节点应力幅值变化均低于5%,故单元尺寸2.5 mm属于网格收敛度较高情形;进而,单元尺寸1.25 mm属于网格收敛度最高情形。
表1 不同单元尺寸下随机选择四处位置的节点应力值变化情况
位置Ⅰ位置Ⅱ位置Ⅲ位置Ⅳ 应力(单元尺寸20 mm)/MPa116.2164.291.89115.8 应力(单元尺寸10 mm)/MPa156.0172.1116.7103.7 应力变化(20 mm到10mm)/%+34+4.8+27-10 应力(单元尺寸10 mm)/MPa156.0172.1116.7103.7 应力(单元尺寸5mm)/MPa187.5177.0126.299.01 应力变化(10mm到5mm)/%+20+2.8+8.1-4.5 应力(单元尺寸5mm)/MPa187.5177.0126.299.01 应力(单元尺寸2.5 mm)/MPa200.4178.4127.496.79 应力变化(5mm到2.5 mm)/%+6.9+0.79+0.95-2.2 应力(单元尺寸2.5mm)/MPa200.4178.4127.496.79 应力(单元尺寸1.25mm)/MPa204.2178.7126.096.27 应力变化(2.5mm到1.25mm)/%+1.9+0.16-1.1-0.54
2.3 车用载具装备有限元网格剖分策略定制
针对车用载具装备,有限元网格的单元尺寸选择还需要考虑有限元仿真分析的计算时间成本,本文仿真分析采用的移动计算工作站性能配置参数如表2所示。
表2 某移动计算工作站性能参数
主要配件配件型号 CPUIntel Core i7-8750H@ 2.20GHz(12CPUs) RAMSAMSUNG DDR4 2666MHz(32.0GB) GPUNVIDIA QUADRO P3200(6GB)
五种不同单元尺寸(20 mm、10 mm、5 mm、2.5 mm和1.25 mm)下的有限元仿真分析的具体计算时间如表3所示。
表3 不同单元尺寸下有限元分析的计算时间
值 单元尺寸/mm201052.51.25 计算时间/min2640260480
由于参与仿真分析的单元节点数目较少,前两个单元尺寸(20 mm和10 mm)有限元模型的计算分析时间均小于10分钟,但根据上一小节的结果,其网格属于未收敛状态,故20 mm和10 mm的网格尺寸选择无法用于车用载具装备结构的工程需求分析。后三个单元尺寸(5 mm、2.5 mm和1.25 mm)的网格收敛度程度不一,收敛度尚可的5 mm单元尺寸计算时间成本最省(40分钟),该网格剖分策略(A)比较适用于对时间成本敏感的拓扑优化等概念设计中;收敛度最高的1.25 mm单元尺寸计算成本最耗时(8小时),该网格剖分策略(C)比较适用于对计算精度侧重的性能评价中,这类仿真通常是单次重分析,对时间成本承受度高;单元尺寸2.5 mm较好地平衡了计算精度和计算时间成本,故网格剖分策略(B)适用于精度和效率兼顾的尺寸优化等详细设计中。具体的车用载具装备有限元网格剖分定制策略如表4所示。
表4 车用载具装备有限元网格剖分定制策略
策略A策略B策略C 单元尺寸/mm52.51.25 工程需求概念设计详细设计性能评价
3 结论
本文提出了一种非标类机械结构有限元网格剖分定制策略的通用流程,并以车用载具装备为算例,分析了五套不同单元尺寸的网格收敛性,确定了收敛程度不一的三套单元尺寸(5 mm、2.5 mm和1.25 mm),继而探究了上述单元尺寸下有限元仿真分析的计算时间成本,从而制定了三套满足不同工程需求的有限元网格单元尺寸选择策略:时间成本最省的策略A,适用于产品的概念设计(拓扑优化设计);兼顾时间成本和计算精度的策略B,适用于产品的详细设计(尺寸优化);计算精度最高的策略C,适用于产品的性能评价(单次重分析)。
[1] 张柏,张兴国,郭旭,等.车间智能物料运载车的发展综述[J].科技资讯,2015,13(26):237-238.
[2] 杨拥军,张勇,何军国,等.XD70/14×12型运载车车架的强度计算[J].石油矿场机械,2012,41(04):72-75.
[3] 熊振浩.轨道平车底架结构分析及优化设计[D].石家庄:石家庄铁道大学,2019.
[4] Wei J, Ma H W. Kinetic characteristics analysis and simulation research on carrier robot[C]//Advanced Materials Research. Trans Tech Publications Ltd, 2012, 346: 359-363.
[5] 吴佳龙.煤矿救援运载车起落架机械结构设计及分析[D].西安:西安科技大学,2014.
[6] Abdullah M A, Tamaldin N, Ramli F R, et al. Design and develop- ment of low cost all terrain vehicle (ATV)[C]//Applied Mechanics and Materials. Trans Tech Publications Ltd, 2014, 663: 517-521.
[7] 刘林丰. 适用于多路况的小型救援运载车设计[D].大连:大连工业大学,2017.
[8] 赵经文,王宏钰.结构有限元分析[M].北京:科学出版社,2001:59-61.
[9] Ahmad M, Ismail K A, et al. Convergence of Finite Element Model for Crushing of a Conical Thin-walled Tube[J]. Procedia Engine- ering, 2013, 53(7):586-593.
[10] Choopanya P,Yang Z.An effective mesh strategy for CFD modelling of polymer electrolyte membrane fuel cells[J].International Journal of Hydrogen Energy, 2016, 41(15):6445-6456.
[11] Dorfler.A Convergent Adaptive Algorithm for Poisson’s Equation[J]. Siam Journal on Numerical Analysis, 1996, 33(3):1106-1124.
[12] Morin, Pedro, Nocheto, et al. Data Oscillation And Convergence Of Adaptive FEM.[J].SIAM Journal on Numerical Analysis,2000,38 (2):466-488.
[13] Binev P, Dahmen W, et al. Adaptive finite element methods with convergence rates[J].Numerische Mathematik,2004,97(2):219- 268.
[14] Cascon J M, Nochetto R H, et al. Design And Convergence of AFEM in H(DIV)[J]. Mathematical Models and Methods in App- lied Sciences, 2007, 20(17):1849-1881.
[15] Carstensen C, Praetorius D, et al.Axioms of Adaptivity [J]. Com- puters & Mathematics with Applications: An International Journal, 2014, 67: 1195-1253.
[16] 刘春梅,钟柳强,舒适,等.平面弹性问题自适应有限元方法的收敛性分析[J].应用数学和力学,2014,35(09):969-978..
[17] 钟德云,王李管,毕林.复杂矿体模型多域自适应网格剖分方法[J].武汉大学学报(信息科学版),2019,44(10):1538-1544.
[18] 胡季,刘春艳,杨玥.基于ANSYS子模型的网格收敛尺寸快速分析方法[J].大连交通大学学报,2019,40(02):57-60.
[19] Patil H,Jeyakarthikeyan P V.Mesh convergence study and estima- tion of discretization error of hub in clutch disc with integration of ANSYS[C].IOP Conference Series: Materials Science and Engine- ering,2018,402(1):12-56.
[20] 刘瑞昌,刘祥斌,宋年秀,等.螺栓连接有限元模拟方法的应用研究[J].制造业自动化,2013,35(23):5-7+21.
[21] 迟秀.典型机械连接结构有限元建模与实验验证研究[D].南京:南京理工大学,2011.
Study of Finite Element Mesh Subdivision Strategy of Customization in a Vehicle Carrier Equipment
LIN Jianyue1, DONG Yanzhang1,2*, CHENG Wenming2, WANG Hui2
( 1.Hubei Key Laboratory of Automotive Power Train and Electronic Control, Hubei University of Automotive Technology, Hubei Shiyan 442002; 2.Hubei DMW Intelligent Group Equipment Co., Ltd., Hubei Shiyan 442002 )
In order to solve the problem of finite element mesh size selection in the simulation analysis and optimization design of non-standard mechanical structures, this paper proposes a general process of customized finite element meshing strategy. Based on the structural finite element model mesh convergence analysis, comprehensively consider the dual effects of finite element convergence accuracy and calculation time cost, corresponding finite element meshing strategies are provided for different analysis and design requirements in structural simulation. The results of the calculation example show that for vehicle equipment, the meshing scheme with the least computational time and cost can greatly reduce the period of the structural conceptual design phase (topology optimization design); the meshing scheme with the highest convergence accuracy can effectively Improve the reliability of structural performance evaluation (single re-analysis); using a compromised meshing scheme can better balance the calculation time cost and convergence accuracy requirements in the detailed design stage (size optimization design).
Vehicle carrier equipment; Finite element mesh; Element convergence analysis; Strategy of customization
U462.2+2
A
1671-7988(2021)20-85-04
U462.2+2
A
1671-7988(2021)20-85-04
10.16638/j.cnki.1671-7988.2021.020.020
林鉴岳(1995—),男,广东湛江人,硕士生,就读于湖北汽车工业学院,从事结构优化设计方面的研究。
董焱章(1983—),男,山东诸城人,副教授,博士,主要从事工程力学、结构与多学科优化、超材料天线设计等方面的研究。
国家自然科学基金青年科学基金(11502075);汽车零部件技术湖北省协同创新项目(2015XTZX0401);湖北汽车工业学院博士科研启动基金(BK201501)资助。
