基于ART神经网络的运行轨迹聚类

薛方，王鹏，王军

基于ART神经网络的运行轨迹聚类

薛方，王鹏，王军

（陕西重型汽车有限公司，陕西 西安 710200）

在商用车大数据研究领域，需在相同路况下对车辆的性能、油耗、载重等进行深入研究，那么就需要将相同轨迹的路线取出来，然后去研究这些路线上车辆的行驶状况。文章要在海量的车辆运行数据（具有时间序列）中，对路线进行聚类。首先使用射线法判断GPS点与区域（可视为多边形）的拓扑关系，得到A市到B市之间的GPS数据，然后对GPS轨迹进行网格化处理，将网格划分为0.01度，得到0-1稀疏矩阵，最后建立自适应共振理论(ART)神经网络模型，对99条样本进行聚类，通过调节阈值的大小，得到合适的聚类结果。

多边形拓扑关系；网格化；稀疏矩阵；聚类；自适应共振理论；阈值

前言

针对具有相同的起点，相同的终点，但中间轨迹不完全相同的GPS轨迹，要从中取出轨迹一致的，以便后续对车的载重、油耗、性能、驾驶习惯等进行研究。本文使用了自适应共振理论（ART）神经网络模型对轨迹样本进行聚类。聚类前需要对原始GPS轨迹数据进行数据预处理，本文用到了射线法[1-3]，网格化稀疏矩阵。首先利用MATLAB自带函数inpolygon，判断点（GPS数据）在多边形（区域）内、多边形（区域）上还是多边形（区域）外，得到驶出A市的时间点，驶入B市的时间点，然后提取该时间段内的GPS信息，即为A市到B市的运行轨迹。其次，进行网格化稀疏矩阵，将运行区域划分为一个个的“网格”。本文将全部样本的运行轨迹的覆盖面进行网格化，计算覆盖面经纬度的最大值和最小值，得到一个区间，对其以0.01度为步长进行网格化，得到每个样本网格化后的0−1矩阵（稀疏矩阵）。最后，使用ART神经网络[4-5]对99个数据处理后的0−1稀疏矩阵进行聚类。

1 点与多边形的拓扑关系判断

为判断车辆何时驶入某个地区，何时驶出某个地区，我们将地区看成一个不规则的多边形，车辆的运行状态借助GPS信息看成点，因此计算车辆何时驶入何时驶出某个区域转化为判断点和多边形的拓扑关系。

（1）点在多边形边界外：就是GPS点未进入观测区域。

（2）点在多边形边界上：就是GPS点在观测区域的边界上。

（3）点在多边形边界内：就是GPS点进入了观测区域内。

本文使用MATLAB自带函数inpolygon识别点和多边形的拓扑关系，得到点在多边形内，点在多边形上，点在多边形外，从而确定每个点和多边形的位置关系。图1是使用函数识别出的点和多边形的位置关系。

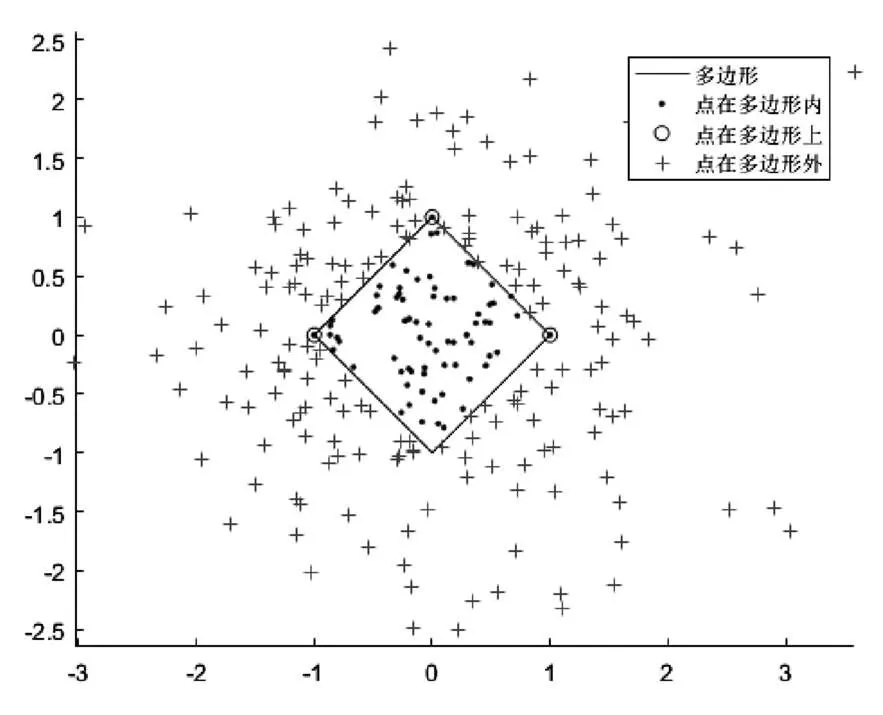
图1 点和多边形的位置关系

2 车辆运行区域识别

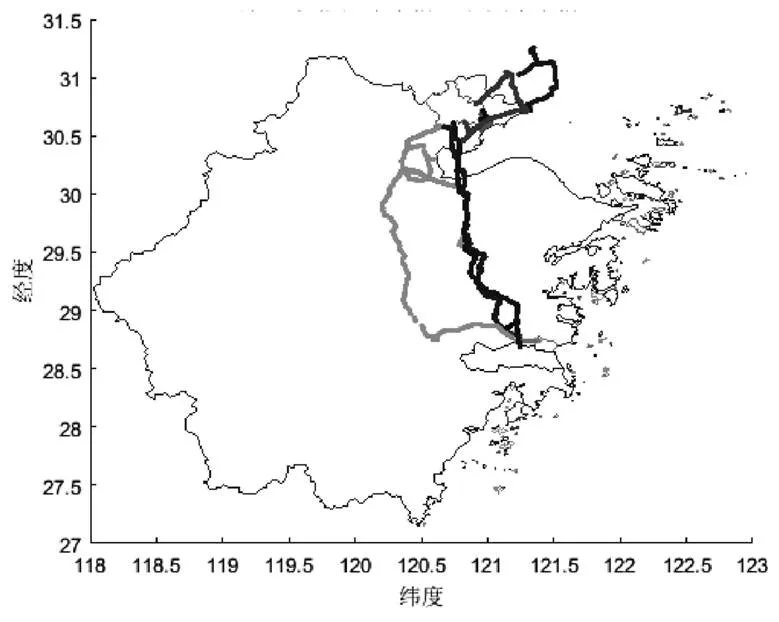
图2 99条路线映射到地图上

在某重卡车型的某细分市场中选取一个月运行数据，根据国家基础地理信息系统数据（网上开源下载）中的省，市，县界限，依据射线法对点与多边形的拓扑关系进行判断，得到了驶出A市的时间，驶入B市的时间，然后提取这段时间内的GPS信息，就得到了99条从A市到B市的路线，见图2。

3 合理划分网格

对全部样本的GPS经纬度覆盖区域进行网格划分，将原来的精度缩减为网格大小，大大减少了计算量。

本文中网格划分的方法如下：

第1步：计算99条样本所覆盖区域的经纬度区间。

经对样本计算得到，纬度（latitude）区间是[28.689 1,31.257 9]，经度（longitude）区间是[120.203 3,121.520 5]。

第2步：设定网格大小。

以经纬度区间为上下限，间隔0.01度生成257×132大小的网格，间隔可以根据实验结果设定。

第3步：划分网格。

如果每个网格里出现GPS经纬度的次数超过1次，那么该网格的值记为1，否则记为0，因此得到0-1矩阵，如图4所示。将全部99个样本都转换为0-1矩阵，接下来要使用ART神经网络算法对0-1矩阵进行聚类。

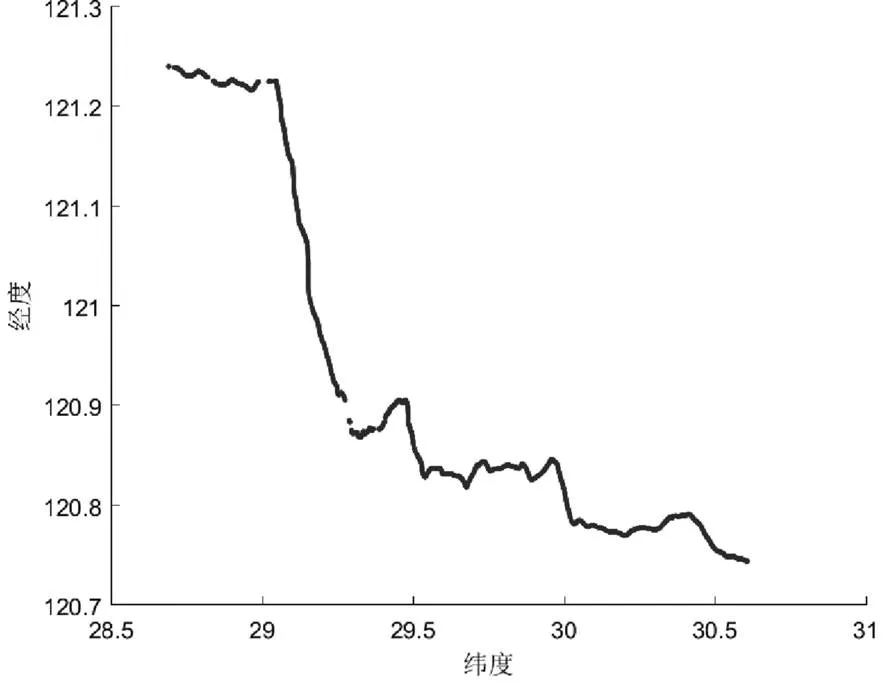
图3 原始GPS轨迹

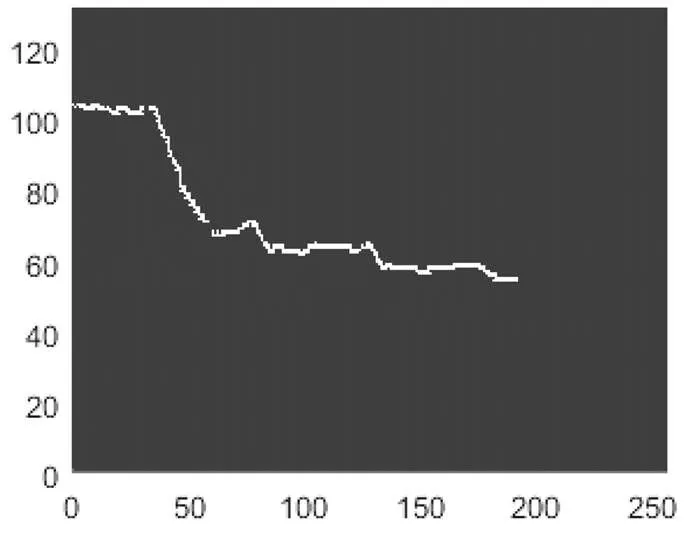
图4 网格化后的轨迹（网格大小为257×132）

4 聚类

4.1 自适应共振理论（ART）神经网络

自适应共振理论（Adaptive Resonance Theory，缩写为ART）网络具有较大地灵活性，可以适应新输入的模式，同时也避免了对网络学习过的模式进行修改。记忆容量可以随样本的增加而自动增加，可以在不破坏原记忆样本的情况下学习新的样本。

ART模型算法步骤：

（1）初始化，设置前向连接权的初值为：w(0)=1/(1+)，其中为输入层单元数，反馈连接权最终将记忆已经学过的输入模式，其值最终为0和1二值的形式，为在开始时不丢失信息，设：t(0)=1,=1,2,…,;=1,2, …,。按需求设识别阈值0＜≤1，识别阈值越大，分类越细；识别阈值越小，分类越粗。

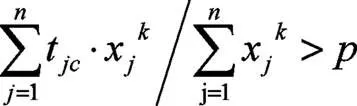
（5）如果小于，取消识别结果，将神经元排除在识别范围之外，返回第（3）步。当所有已记忆过的神经元都不满足（4）时，则在输出层增加一个神经元，并令这个神经元为神经元的连接权和反馈连接权均为X。

（6）按下式调整连接权和反馈连接权：

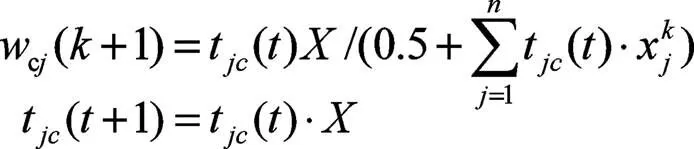
（7）返回第2步，对下一个输入模式进行识别。

4.2 实验结果

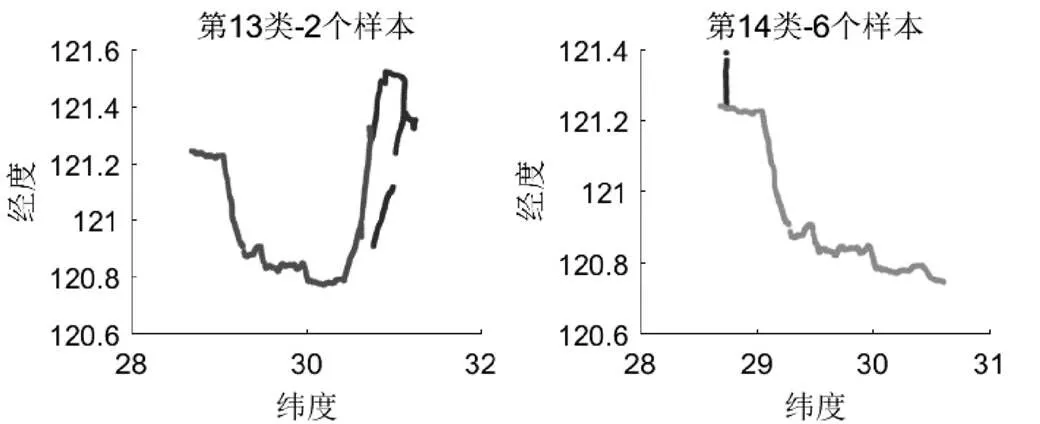
对合理划分网格得到的99个0−1矩阵使用自适应共振理论（ART）网络算法，建立=339 24，=99的网络，然后设置识别阈值进行聚类，识别阈值的大小决定聚类的程度，针对本文样本，识别阈值等于0.94的情况下得到以下分类结果：99个样本分为17类，其中第1类有66个样本，在进行车辆性能测试，油耗比对，载重估计，驾驶行为等研究时，我们通常选择聚类样本较多的某些类进行深入研究。

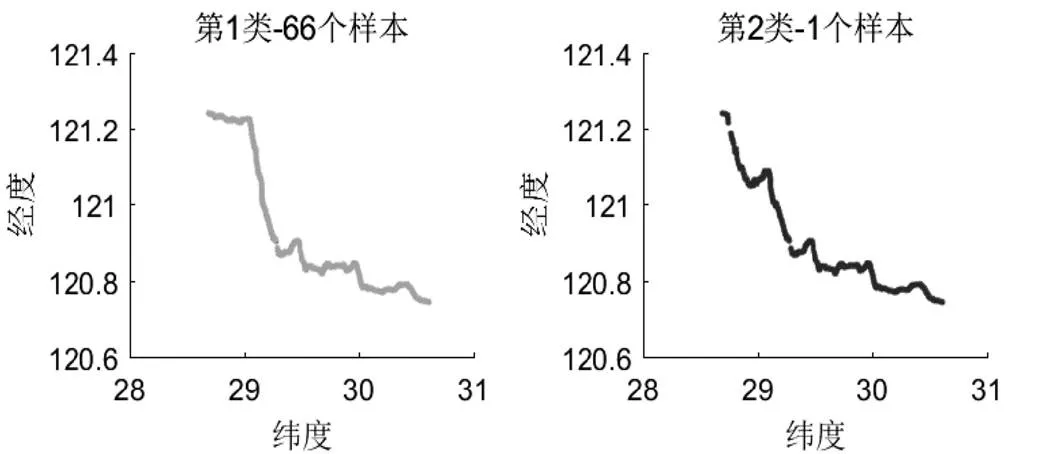
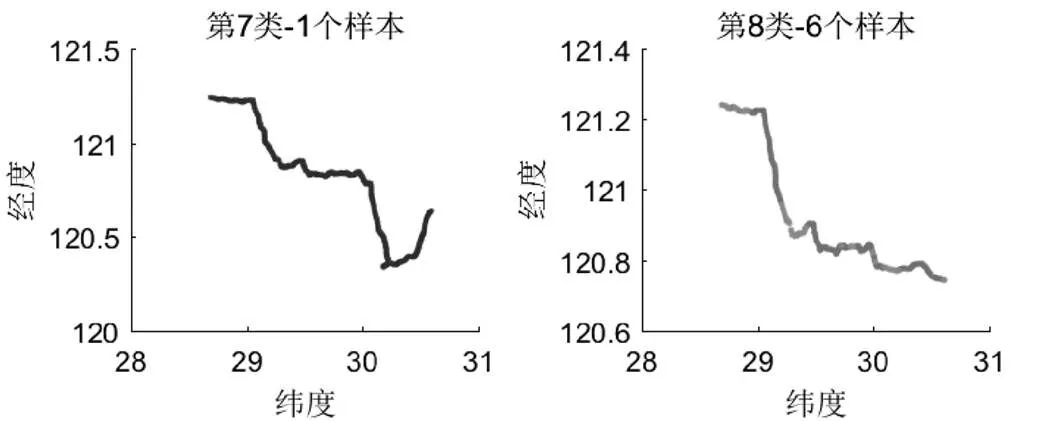
5 结语

本文以真实的GPS轨迹为输入数据，经过数据预处理得到0−1稀疏矩阵，再使用自适应共振理论（ART）神经网络算法对其进行聚类，得到轨迹一致的路线，方便对车辆性能的深入研究和应用，聚类效果好。

[1] 常胜,宋鄂平.射线法的完善及其在地理信息系统中的应用[J].湖北民族学院学报（自然科学版）,2004.3,22(1):91-93.

[2] 翟艳,徐卫亚,张强.点与多边形或多面体的拓扑关系判断[J].计算机工程与设计,2015.4,36(4):972-975.

[3] 向俊,王静,夏幼明.判断点与多边形拓扑关系的改进算法[J].计算机工程与设计,2014.5,35(5):1732-1737.

[4] 杨戈,莫青青,黄静.基于ART1网络的字符识别器[J].计算机系统应用,2014,12(23):136-141.

[5] 韩可轶,周德俭,张烈平,等.基于人工神经网络自适应共振理论的手写字符识别[J].桂林工商学院学报.2006,26(1):122-124.

Trajectory Clustering Based on ART Neural Network

XUE Fang, WANG Peng, WANG Jun

( Shaanxi Heavy Duty Automobile Co., Ltd., Shaanxi Xi’an 710200 )

In the research field of big data of commercial vehicles, the performance, fuel consumption and load of vehicles should be studied in depth under the same road conditions. Then, the routes with the same trajectory should be taken out and the driving conditions of vehicles on these routes should be studied. In this paper, the route is clustered in the massive vehicle operation data (with time series). Firstly, the topological relationship between GPS points and regions (which can be regarded as polygons) is determined by ray method, and the GPS data between A city and B city is obtained. Then, the GPS track is processed by grid. The mesh is divided into 0.01 degree and 0-1 sparse matrix is obtained. Finally, an adaptive resonance theory (ART) neural network model was established to cluster the 99 samples, and the appropriate clustering results were obtained by adjusting the threshold value.

Polygon topological relation; Grid; Sparse matrix; Cluster; ART; The threshold value

P228.4

A

1671-7988(2021)20-37-04

P228.4

A

1671-7988(2021)20-37-04

10.16638/j.cnki.1671-7988.2021.020.010

薛方（1989—），女，硕士，工程师，就职于陕西重型汽车有限公司，研究方向：数据挖掘，机器学习，深度学习，控制策略。