棒束子通道CHF机理模型开发及初步验证

桂民洋，田文喜，吴 迪，陈荣华，张 魁，苏光辉，秋穗正

(西安交通大学 核科学与技术学院，陕西 西安 710049)

在核反应堆的设计与安全分析中，临界热流密度是重要的限制性热工参数，它直接影响核反应堆的安全性和经济性。临界热流密度是指沸腾传热机理发生变化而使核燃料元件表面发生传热恶化时发热元件表面单位面积产生的热量，如果反应堆燃料元件表面发生沸腾临界，将会导致燃料元件表面温度过高从而造成加热壁面烧毁，放射性物质泄漏，进而造成严重的反应堆运行事故[1]。因此，准确预测临界热流密度对反应堆热工水力设计和安全分析有着十分重要的意义。临界热流密度模型一般分为两类：偏离泡核沸腾(DNB)型和干涸型。常用的预测方法主要有经验关系式和临界热流密度查询表(CHF look-up table)[2]。

但受限于特定流体种类、热工边界、几何尺寸等实验条件，大多数实验关系式的适用范围不能轻易外推，或外推后预测精度下降。因此，一些学者转而从临界发生时的微观机理入手，力图获得适用范围更广的临界热流密度机理模型。如Weisman等[3]、Ying等[4]提出的近壁面气泡壅塞模型，他们认为，发生临界时壁面附近大量汽泡聚集形成一个汽泡层，当汽泡层外沿处的液相流动减弱到不能穿透汽泡层到达加热壁面时，汽泡层的汽泡会结合形成汽泡膜阻隔传热从而发生DNB；而Lee等[5]、Liu等[6]针对DNB提出了微液层蒸干模型，认为壁面附近会有由多个小汽泡结合而形成一个拉长的大汽块，汽块下存在一层很薄的微液层，当微液层蒸干时即发生临界。对于干涸，其主要发生在环状流末期，此时液滴的作用显著，因而大多数学者主要关注环状流流型区液滴的夹带沉积现象[7-12]。

作为反应堆堆芯热工水力分析的重要工具，子通道程序中临界热流密度基本通过实验关系式求得，而本文则基于临界热流密度机理模型，通过与子通道分析方法耦合，实现对棒束通道内临界热流密度的预测，其中子通道程序用于计算通道中的焓分布和流量分布，为临界热流密度机理模型提供边界条件，进而判断临界的发生。

1 数学物理模型

本研究中考虑3类模型，即子通道模型、DNB型和干涸型临界热流密度机理模型。其中，子通道模型基于SACOS子通道程序[13]。

1.1 子通道模型

子通道内流体的流动包含轴向和横向两个方向，其控制方程组(连续方程、能量方程、轴向动量方程和横向动量方程)如下。

连续方程：

(1)

式中：i、j为相邻通道编号；Ai为通道i流通截面积，m2；ρi为通道i流体密度，kg/m3；mi为通道i轴向质量流量，kg/s。

能量方程：

(2)

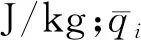
轴向动量方程：

(3)

式中：pi为通道i的压力，Pa；g为重力加速度，m/s2；θ为通道倾斜角度，(°)；fT为横向动量因子；ui为通道i的轴向流速，m/s；uj为通道j的轴向速度，m/s；u*为通道间横向搅混流体流速，m/s；fi为通道i的摩擦系数；Di为通道i的等效水力直径，m；Ks为局部阻力系数；Δz为轴向控制体高度，m。

横向动量方程：

(4)

式中：sij为通道i与j间隙长度，m；lij为通道i与j间搅混长度，m；KG为通道i与j间横流阻力系数；ρ*为通道间横流冷却剂密度，kg/m3，为来流通道的冷却剂参数。

1.2 DNB型临界热流密度机理模型

DNB型临界热流密度机理模型主要基于微液层蒸干模型，假设加热壁面附近产生的小汽泡结合形成大汽块，在汽块下存在非常薄的液相层，称为微液层，当微液层蒸干即发生临界，如图1所示。

图1 微液层蒸干模型示意图

微液层蒸干所对应的热流密度可表示为：

qDNB=ρfδhfgUB/LB

(5)

式中：δ为汽块下微液层厚度，m；hfg为汽化潜热，kJ/kg；UB为汽块移动速度，m/s；LB为汽块长度，m。

在微液层蒸干模型中，汽块下微液层厚度δ、汽块移动速度UB与汽块长度LB是模型求解的3个关键参数。其中，汽块移动速度可通过轴向方向施加在汽块上的浮力FB和拖拽力FD的平衡得到，即：

FB=FD

(6)

最终可得到汽块速度的表达式为：

(7)

式中：UBL为汽块径向位置处的主流速度，m/s；CD为拖拽系数。

汽块的长度LB假设为Helmholtz临界波长，可得：

(8)

微液层的厚度δ由径向方向施加在汽块上的力的平衡来确定，主要考虑蒸发力FE、侧面提升力FL[5]、壁面润滑力FWL和Marangoni力FM[6]。最终可得其表达式为：

(9)

式中：DB为汽块当量直径，m；q为加热壁面热流密度，W/m2；CWL为壁面润滑系数；CL为提升力系数；G为通道质量流密度，kg/(m2·s)。

图2为微液层蒸干模型计算流程图。

图2 微液层蒸干模型计算流程图

1.3 干涸型临界热流密度机理模型

干涸型临界热流密度机理模型主要基于环状流液膜蒸干模型。加热通道内饱和沸腾区两相流流型如图3所示，主要经历了泡状流、搅混流，最后形成环状流直到液膜逐渐烧干。通道内环状流的特点是液膜在沿着通道壁面流动，同时夹带有液滴的汽芯在通道中央流动。

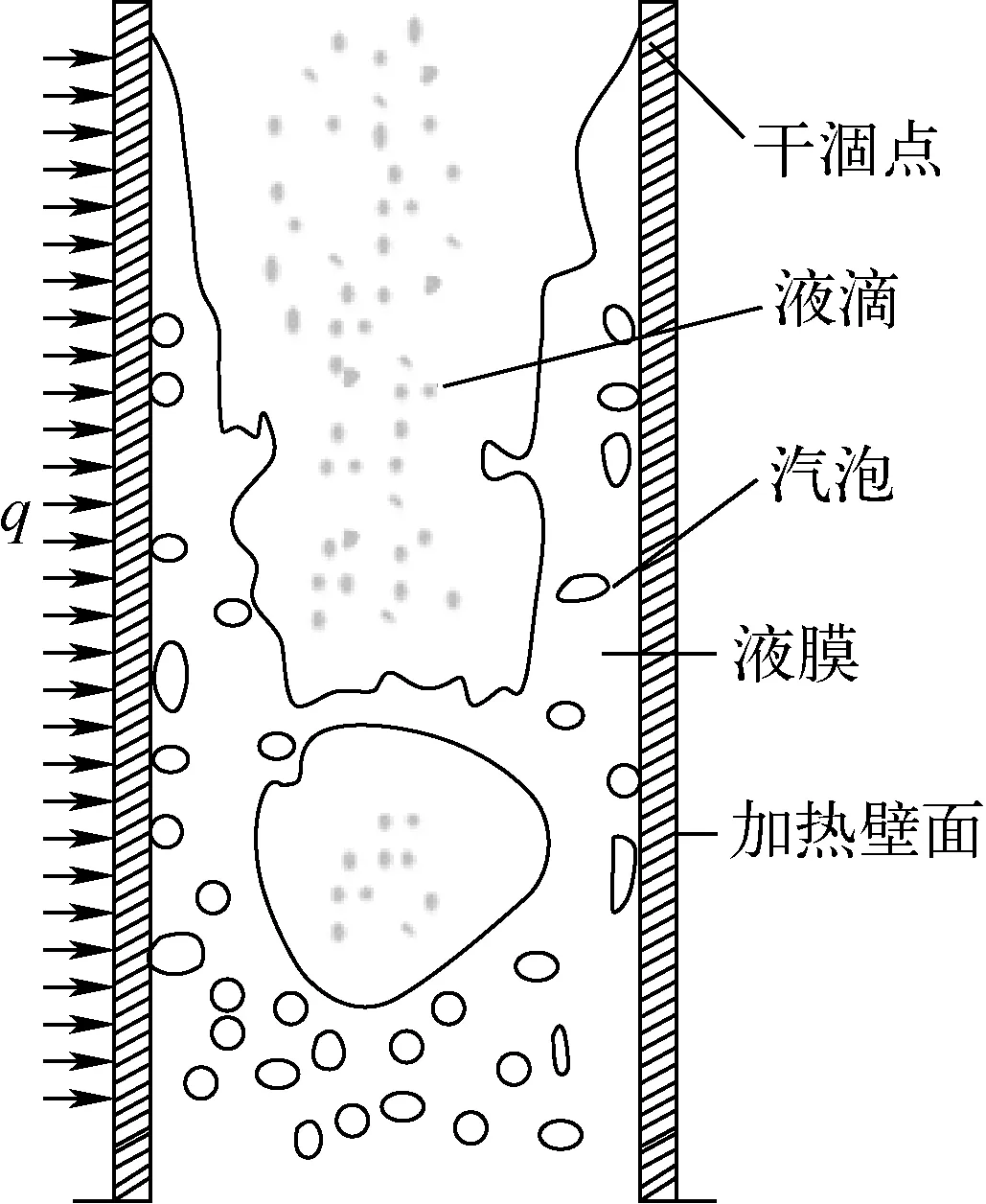
图3 环状流液膜蒸干模型示意图

在环状流区域存在液膜蒸发、液滴夹带和液滴沉积的复杂现象，干涸的发生可认为是三者之间相互竞争的结果。考虑沿通道轴向液膜质量流量的变化，可得到液膜质量流量的控制方程：

(10)

式中：Wf为液膜质量流量，kg/s；md为液滴沉积率，kg/(m2·s)；me为液滴夹带率，kg/(m2·s)；mv为液相蒸发率，kg/(m2·s)；P为通道湿周(加热周长)，m。

一旦确定了环状流起始点，通过引入液滴夹带沉积的本构关系式，由式(10)可得到沿轴向壁面液膜质量流量的变化趋势，当液膜质量流量为0时，即认为发生干涸。

1) 环状流起始点

环状流起始点采用Wallis[14]的理论，其推荐如下由搅混流到环状流转变的关系式：

(11)

(12)

即可通过通道内含汽率确定环状流起始点。

2) 液滴的夹带和沉积率

液滴的夹带率和沉积率关系式选用Okawa模型[9]，它是基于大量的液滴实验数据拟合而来，对于沉积率md，其与气相中液滴浓度C有关：

md=kdC

(13)

式中，kd为液滴沉积系数，表达式为：

(14)

(15)

针对液滴夹带率，从夹带产生的机理出发，主要考虑两类效应：中心气相对液相的剪切夹带(液相雷诺数Ref>320)和气液界面处气泡的破裂造成的夹带，即：

me=me1+me2

(16)

对于前者，Okawa提出了如下关系式：

(17)

式中：fi为相间剪切应力系数；Jg为气相表观速度，m/s；δ为液膜厚度，m；σ为表面张力，N/m。

对于后者，采用了Ueda等[15]建立的夹带关系式：

(18)

3) 液相的蒸发率

模型中假设环状流区域液膜处于饱和状态，则加热壁面的热量全部用于液相的蒸发，则液相的蒸发率为：

mv=q/hfg

(19)

2 子通道模型与机理模型的耦合

子通道程序已被证明可较好地计算棒束通道中的流量和焓，得到通道中的流量和温度分布；而临界热流密度机理模型从微观机理现象入手，可克服经验关系式对几何条件、热工边界条件的限制要求，通过两者的耦合计算，可充分发挥各自的作用。但一般的机理模型是基于单通道提出的，对于子通道还需考虑通道间的质量、能量搅混，因而对于两者耦合还需做特殊的处理。

2.1 子通道模型与DNB型机理模型的耦合

一般情况下，DNB主要发生在过冷沸腾区，若通道轴向均匀加热，则DNB最先发生在出口；但通道轴向功率非均匀分布时，DNB在通道出口之前某处就有可能发生，因此，为充分考虑非均匀加热，轴向通道将被分为若干个控制体，由子通道程序计算得到通道的流量、焓参数传递给机理模型，每个控制体作为单独通道均调用机理模型进行计算。考虑到径向功率的不均匀性(如1个子通道为4根加热棒中间围成的区域)，保守来看应取径向热流密度最大值与式(5)所求的qDNB进行比较，从而判断该位置处是否发生DNB，耦合后的程序计算流程如图4所示。

图4 DNB模型与子通道分析的耦合计算

特别地，为考虑通道间能量搅混，模型中热流密度需由进出口焓进行修正，即：

(20)

式中：qj为轴向控制体j中热流密度，W/m2；hout为轴向控制体j出口焓，J/kg；hin为轴向控制体j入口焓，J/kg；G为轴向控制体j质量流量，kg/(m2·s)；A为轴向控制体j流通面积，m2；Det为轴向控制体j加热直径，m；l为轴向控制体j轴向长度，m。

2.2 子通道模型与干涸型机理模型的耦合

液膜蒸干模型是基于单通道(如圆管、矩形通道)提出的，其与子通道模型的耦合需考虑子通道特殊的结构形式，如图5所示。典型的子通道包含角通道、边通道和中心通道，一方面，机理模型需考虑通道间的质量、能量搅混；另一方面，需考虑径向功率的非均匀性，如图3中的角通道和边通道，由于存在非加热壁面，因此壁面液膜轴向质量方程中不存在蒸发项mv，对于中心通道，由于其周围加热棒功率的不一致性，导致液膜厚度不同，也需分开考虑。

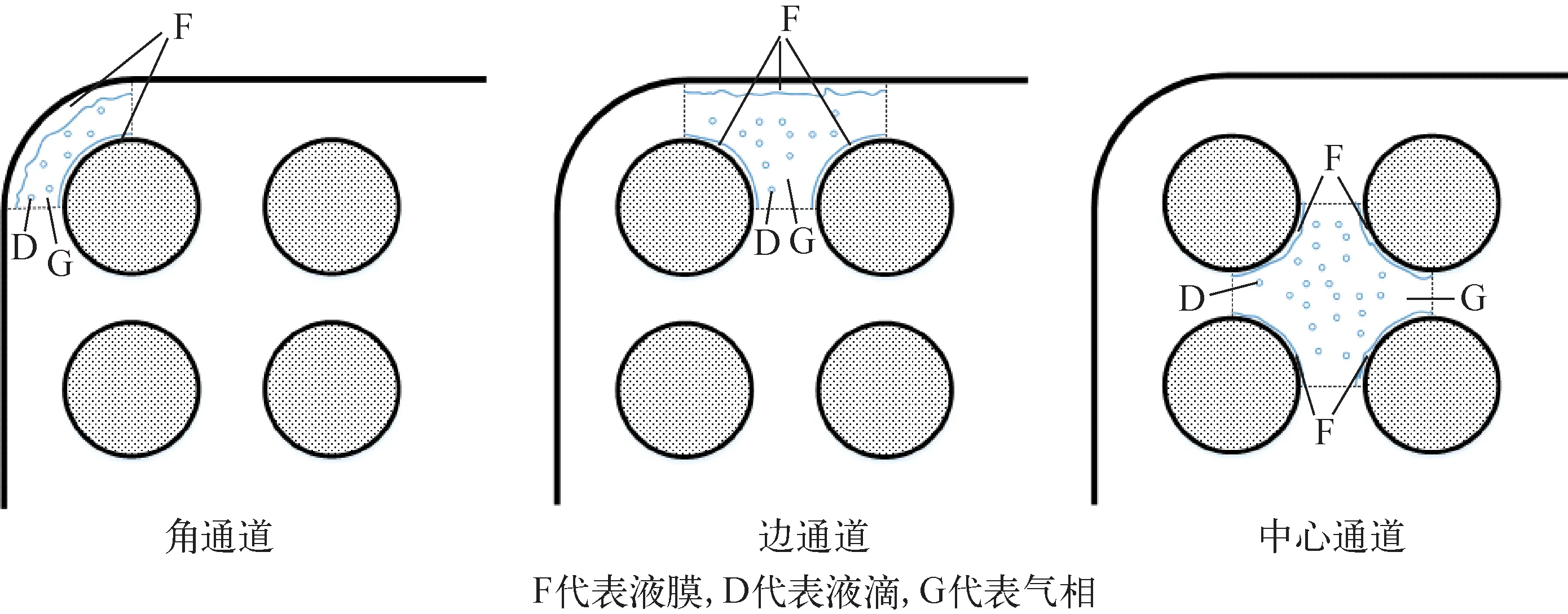
图5 棒束中液膜蒸干模型示意图

因此，考虑干涸型机理模型在子通道中的应用，式(10)液膜质量流量的控制方程需改为以下形式：

(21)

式中：k为液膜标识(k=1～N)；wl为子通道间液相横向流质量流量，kg/(m·s)；ζf为横向流中液膜所占份额。

1个子通道中液膜可分为N份(对于角通道N=2，对于边通道N=3，对于中心通道N=4)，它们共用同一区域的气相和液相，对于液相横向流，可由子通道程序计算得到，而液相又可分为壁面流动液膜和中心夹带的液滴，程序中两者的比例ζf可认为和通道中液膜与液滴的浓度比相同。

总地来说，由子通道程序计算得到各通道环状流起始点，可认为起始点处液膜均匀覆盖在各壁面上，同时由子通道程序可确定通道间流体的横向流动，即可通过液膜质量守恒方程及相关本构方程确定各壁面轴向液膜质量流量变化趋势，当某一壁面液膜质量流量或空泡份额趋于0时即认为发生干涸，耦合后的程序计算流程如图6所示。

图6 蒸干模型与子通道分析的耦合计算

3 验证和分析

子通道程序与临界热流密度机理模型耦合的验证基于EPRI的CHF实验数据库[16-17]，实验工况包含压水堆(PWR)和沸水堆(BWR)，可用于DNB型和干涸型临界热流密度机理模型的验证，通道类型主要为4×4棒束和5×5棒束，具体的通道几何与热工边界参数列于表1。

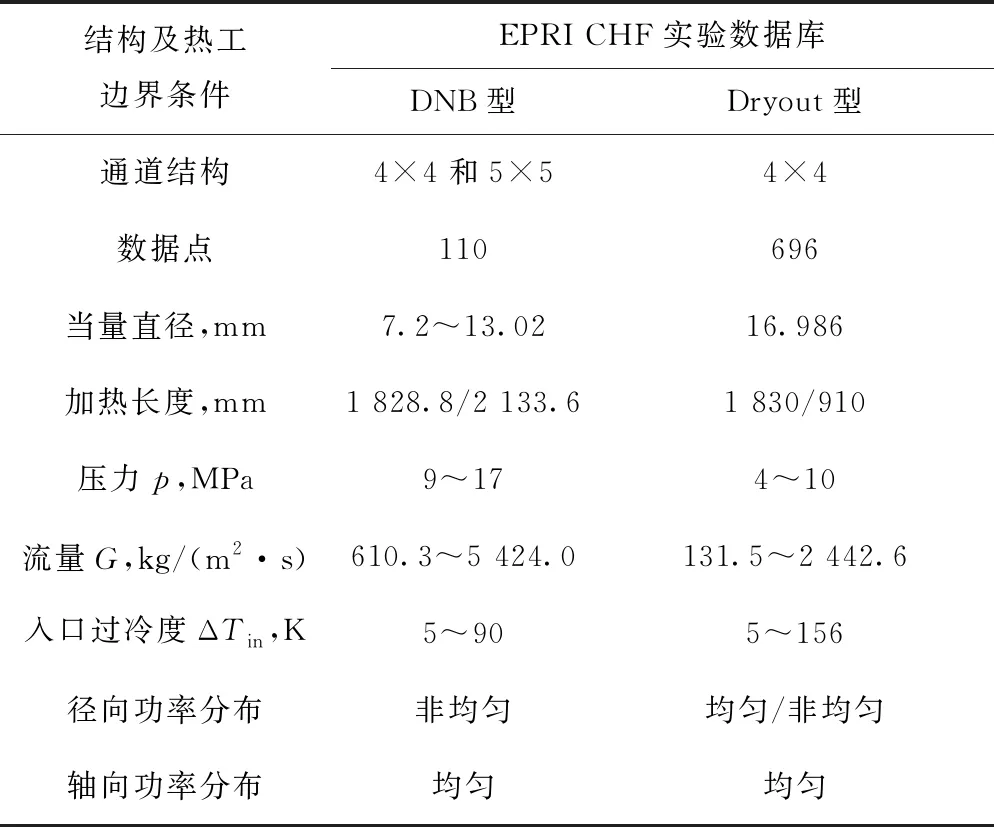
表1 临界热流密度机理模型验证数据

本文中，首先由SACOS子通道程序建立棒束通道的几何模型，给定边界条件，包括出口压力、入口流量、入口温度和平均功率密度，通过子通道程序计算通道各处局部参数，进而调用DNB或干涸型临界热流密度机理模型计算，逐渐增大平均功率密度，直至发生临界。图7～10示出了模型计算值与实验值的对比结果，其中图7、8为DNB型临界热流密度的对比结果，图9、10为干涸型临界热流密度的对比结果。

从图7可看出，验证数据点为110个，94.4%的数据点误差在20%之内，机理模型对CHF的预测趋势与实验结果一致。从图8可看出，机理模型的预测结果满足一般规律，且与实验结果相比有较好的一致性，临界热流密度(q)随系统压力的升高、入口过冷度的增大和入口流量的增大而增大。本文的DNB型临界热流密度机理模型是基于Lee和Mudawar[5]最早提出的微液层蒸干模型改进而来，其中微液层的存在也被一些可视化实验所证实。但机理模型中仍存在经验系数需人为确定，这也是模型计算误差的主要原因。其主要表现在式(9)中的提升力系数CL，Lee和Mudawar提出了仅与雷诺数Re相关的CL表达式：

图7 DNB型临界热流密度总体验证结果

图8 DNB型临界热流密度的变化

CL=a1Rea2

(22)

而Beyerlein等[18]建议CL是平均空泡份额和Re的函数，即它与紊流波动和当地汽泡分布情况有关。基于此，本文中模型采用的CL表达式为：

CL=230Re-0.35-0.23exp(1.8α)

(23)

式中，CL的经验处理使得模型计算值存在偏差，且具有一定的不确定性。可预料，当不断修正上式中的常数时，可获得与实验值更为接近的预测结果。

从图9可看出，验证数据点为696个，95.8%数据点误差在20%之内，机理模型对CHF的预测趋势与实验结果一致，显示了模型较好的预测能力。从图10可看出，临界热流密度随入口过冷度和流量的增大而增大，随系统压力的增大而减小，与实验趋势相同。总体来看，干涸型机理模型可较为真实地反映棒束通道中壁面附着的液膜逐渐减薄至发生干涸的物理过程，两者存在的偏差有两个方面的原因：一方面，机理模型中液滴夹带沉积模型存在计算偏差，目前关于液滴的夹带沉积模型多基于有限的实验数据，且受限于特定的适用范围，关系式的扩展性较差，因而引入了一定的不确定性，另一方面，目前干涸型临界热流密度机理模型中并未考虑格架的影响，通常格架的存在会增强液滴的横向运动，进而改变液滴的沉积率，因此会影响临界热流密度。

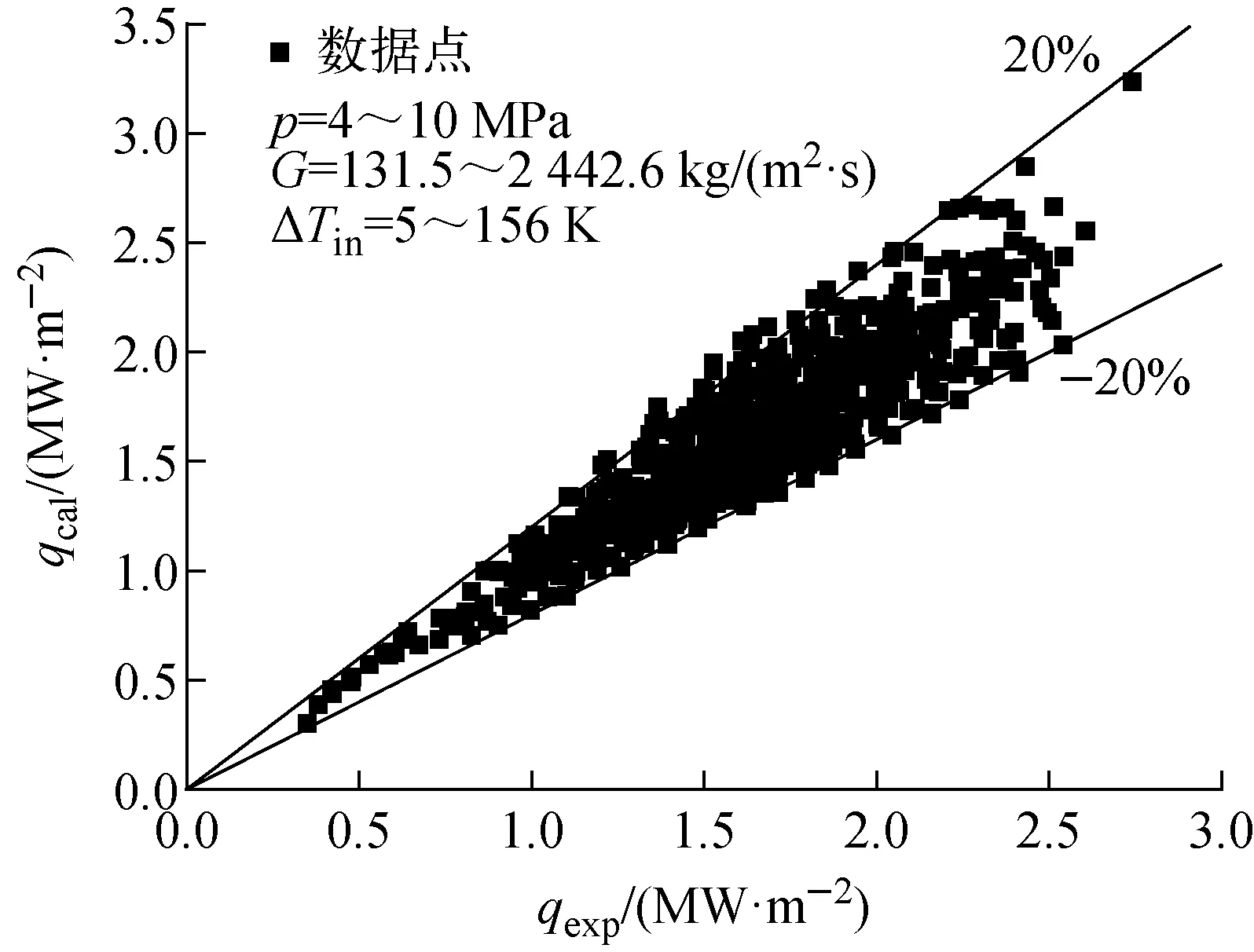
图9 干涸型临界热流密度总体验证结果

图10 干涸型临界热流密度的变化

4 结论

本研究以子通道模型为基础，通过耦合DNB型和干涸型临界热流密度机理模型，实现了对棒束通道内临界热流密度的预测，其中借助于子通道程序计算通道中的焓分布和流量分布，为临界热流密度机理模型提供边界条件，进而判断临界的发生。通过与临界热流密度实验数据对比发现，耦合程序对棒束通道中临界热流密度具有较好的预测精度，临界热流密度预测值随相关热工参数的变化规律与实验相比也有较好的一致性。

本研究中，基于棒束子通道的临界热流密度机理模型可有效弥补目前实验关系式适用范围受限的不足，也可为后续临界热流密度实验工况设计提供参考，但需注意的是，目前的研究中临界热流密度模型的验证范围仍有限，因此在后续的研究中有必要进行更为充分的验证。同时，对于干涸现象，中心气相、液膜和液滴的理论被普遍接受，除液滴的夹带和沉积关系式外，模型中的不确定因素较少，而对于DNB现象，除微液层蒸干模型，还有近壁面汽泡壅塞、边界层分离和界面提升等理论，模型中的不确定性参数也较多，因此后续的研究也需进一步探讨临界热流密度机理模型的可靠性。