顾及表层声速和坐标先验信息的海底控制点定位方法

李治远，吴永亭，胡 俊，豆虎林

(自然资源部 第一海洋研究所,山东 青岛 266061)

海底控制网是海洋大地测量的基础,对探测和监测海洋板块运动及地壳变形有重要意义[1-2]。在控制点绝对位置确定过程中,Spiess[3]、Kussat等[4]以及Chen和Wang[5]利用GPS和声学测量结合的方法研究了海底地壳运动,基于此,一些国内外学者相继做了进一步研究[6-10]。其基本思想都是利用船载GPS和水下测距设备,交会确定海底控制点坐标,但是测距精度受到声速误差影响较大,即使声速误差非常小,也会引起海底控制点定位精度大幅下降,因此,声速误差引起的定位误差是不可忽视的[11-12]。为削弱声速误差带来的影响,并提高定位精度和作业效率,Chen提出了圆走航法[13]。基于测量船轨迹的对称性,利用最小二乘求解控制点坐标可以有效削弱声速误差的影响,但圆走航法存在垂直解精度低且不稳定的问题。引入深度传感器的测深值可有效提高垂直解的精度,任国晶[14]研究表明采用深度传感器可以获得精度优于水深0.1%的深度信息。赵建虎等[15]提出了一种附加深度约束的海底控制点三维坐标确定方法,将深度传感器测得的水深作为新的观测量引入平差模型,并在松花湖水域进行了水下实验,结果表明,引入深度约束条件后,控制点垂直解的精度提高了2～5倍。在附加深度约束的海底控制点三维坐标定位方法中,精确的距离测定是必要前提,准确的声速剖面则是精确测距的关键,但是频繁的声速剖面测量费时费力[16-17],在深远海不具备测量条件。为解决不易频繁施测声速剖面而无法获得高精度、稳定的海底控制点三维绝对坐标问题,基于圆走航法,本文提出了一种顾及表层声速和坐标先验信息的海底控制网点定位方法。首先,考虑圆走航法的对称性,开展声速误差对海底控制点平面坐标精度影响的研究,建立利用表层声速求解海底控制点平面坐标先验值的模型；然后,建立仅需表层声速及深度信息的海底控制网点精密定位方法；最后,根据这些方法进行模拟实验验证,以期在仅利用表层声速的条件下,能得到与利用声速剖面的三维约束平差方法同精度的定位结果。

1 圆走航模式声速误差分析

圆走航法是利用测量船在水面围绕海底控制点绕圆航行,借助每个时刻GNSS提供的船位、船载换能器到海底控制点间的测距值,交会得到海底控制点坐标的方法。测量船在水面围绕海底控制点以某一半径进行圆轨迹走航,并等间隔地测量n个航迹点,即可获得每个航迹点处船载换能器与海底应答器之间的双程传播时间,根据时间及初始入射角进行声线跟踪即可得到换能器与应答器之间的几何距离。

由于圆走航轨迹是一个以待定点为圆心的圆,因此在每个航迹点处声线的入射角是近似相等的,且海底地形较为平坦,声线传播时间也近似相等。由声线跟踪原理可知,当入射角和声线传播距离相等时,一定区域内声速误差引起的测距误差也是相等的,故可以认为所有航迹点处的测距误差是相等的[18]。若海底控制点和船载换能器的坐标分别为xo和x i,则观测方程为

式中,ρoi为海底应答器与换能器之间的观测距离,f(xo,x i)为应答器与换能器之间的几何距离,δSoi为应答器延迟引起的等效误差,δρoi为声速误差引起的等效误差,εoi为偶然误差。根据最小二乘原理[19],δρoi对定位结果影响的表示方程为

圆走航模式下,每个航迹点处距离测量精度基本相等,因此权阵P取单位阵。BTB可展开为

式中,A i为航迹点与圆心连线的地理方位角,θi为该航迹点处声线入射角。由于声线入射角近似相等,因此式(3)中θi为定值,且航迹点均匀分布,关于圆心对称,因此有:

则式(3)可以简化为

于是,可以进一步将式(2)展开,得到

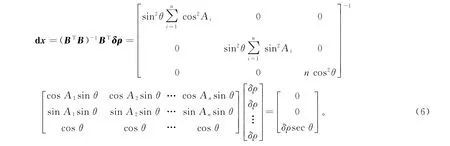
由式(6)可知,圆走航模式下,声速误差对控制点水平坐标精度没有影响,仅反映在垂直方向上,且对控制点垂直坐标的影响与声速误差δρ成正比。

2 顾及平面坐标先验信息的海底控制点坐标确定

2.1 控制点平面坐标先验值获取

设海底控制点坐标为Xo(xo,yo,zo),第i次观测时船载换能器坐标为X i(x i,y i,z i),声线在两点之间的单程传播时间为t i,表层声速为vs,则观测距离S i近似等于vst i,观测方程为

式中:f(Xo,X i)为控制点和换能器之间的空间斜距,且f(Xo,X i)＝δSo为应答器延迟等效误差；δSv为声速等效误差；ε为偶然误差。在文中的圆走航模式声速误差分析中已经证明,圆走航模式下声速误差仅对控制点垂直解的精度有影响,此处我们只关注控制点平面坐标,因此可忽略δSv,式(7)对应的误差方程为

每个航迹点处都可建立式(8)的误差方程,共可得n个误差方程。根据最小二乘原理,验后单位权中误差估值及控制点坐标精度为

至此,即可获得控制点水平坐标先验值(xo,yo)及其先验方差D x和D y。

2.2 顾及坐标先验值的精密定位

假设换能器在t i时刻的位置为X i,其坐标通过船载GNSS天线及其与换能器的位置关系确定。海底控制点坐标是待求量,设为Xo；t i时刻测得声线从换能器传播至海底应答器的时延为τi,利用表层声速vs乘以时延可得到近似距离ρi,参考式(7),可以得到观测方程:

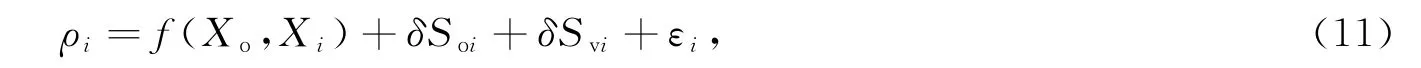
线性化之后得到:

式中,为Xo的先验值,水平坐标先验值由式(10)获得,垂直坐标先验值使用控制点上压力传感器测得的水深值。B i是根据和X i计算得到的f(Xo,X i)关于Xo的一阶偏导数。

控制点上的应答器内置压力传感器可提供较精确的水深,但由于其测量值为瞬时海面至应答器中心处的垂直距离,不可避免地会受到波浪影响而带有误差[20]。因此,直接将压力传感器测得的水深作为已知量是不合适的。将观测水深视为新的观测量,其先验方差根据经验值给定,一般为水深的0.1%,而平面坐标先验值及其方差在式(10)中已经求得。因此,将控制点坐标视为待求量,考虑其先验随机信息,采用广义最小二乘原理进行求解,误差方程为

式(13)中:前3式为虚拟观测方程[19],μx、μy和μz为控制点三维坐标的先验期望；第四式为式(12)对应的误差方程。设控制点三维坐标的先验方差分别为D x、D y和D z,观测值方差阵为DΔ,则此时μx、μy、μz和L的方差阵为

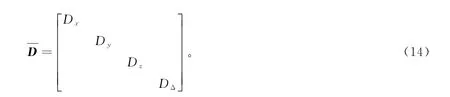
考虑到x、y、z和L互相独立,其方差阵为对角矩阵。引入虚拟观测值后,可将控制点三维坐标视为非随机量,采用经典最小二乘法求解,因此,控制点三维坐标可通过Xo＝求得,其中和为引入虚拟观测值后的扩展误差方程系数矩阵、观测值方差阵和误差方程常数项。

3 实验及分析

为验证本文提出方法的有效性,分别模拟了50 m 水深(Z)和1 500 m 水深处的实验,利用圆走航法,以海底应答器为圆心确定海底控制点的三维坐标。实验过程中,忽略GNSS接收机天线至换能器之间的坐标转换,直接给出换能器以海底应答器为圆心、半径为水深值1/2的圆走航轨迹(图1a)。声速剖面采用50 m和1 500 m 水深两处海域的实测数据,考虑到换能器的吃水,表层声速取4 m 水深处的声速剖面值(图1b和图1c)。应答器上内置的压力传感器测得的水深数据分别在50 m 和1 500 m 基础上附加振幅为－0.5～0.5 m的波浪效果。

图1 航迹图及实验区域声速剖面Fig.1 Track plot and sound velocity profiles in the testing area

根据圆走航法测量获得的换能器到应答器间时延、船载GNSS提供的换能器坐标及应答器内置压力传感器测得的控制点水深和换能器表层声速数据,采用3种数据处理方法(方法A、B 和C),计算海底控制点三维坐标。

①基于声线跟踪的精密定位方法(方法A):采用声线跟踪获得较为准确的观测距离,利用距离交会定位原理,结合应答器提供的水深信息平差求得控制点坐标最优解并评定精度。

②基于表层声速的三维定位方法(方法B):仅利用声线传播时间乘以表层声速得到换能器与水听器之间的几何距离,利用交会定位原理,平差求得海底控制点绝对坐标,并评定解算结果的精度。

③顾及水深信息及控制点坐标先验信息的精密定位方法(方法C):利用声线传播时间乘以表层声速得到换能器与水听器之间的几何距离,并引入控制点平面坐标先验值及深度传感器提供的水深信息作为控制点坐标先验信息,采用广义最小二乘原理求解控制点三维坐标,并评定其精度。

以控制点绝对坐标为参考,将3种数据处理方法结果分别与其进行比较,可得控制点坐标外符合精度(表1),结果能较为真实地反映数据处理结果的准确性。由表1可知:①3种方法的平面定位精度都较高。50 m 水深时,平面精度基本处于0.05 m；1 500 m 水深时,平面精度基本处于0.5 m。方法B中,观测距离由表层声速与声线传播时间的乘积直接得到,由此可以证明,在圆走航模式下,声速误差对控制点平面位置的影响基本可以忽略不计,这与文中圆走航模式声速误差分析的结果相符。②方法A 和方法C的控制点垂直坐标精度明显高于方法B。50 m 水深时,前两者精度为厘米级,后者达到分米级；1 500 m 水深时,前两者精度为亚米级,后者达到米级。比较方法A 和方法B的控制点垂直坐标精度可以看出,方法B得到的精度远低于方法A,这说明在圆走航模式测量中,声速误差虽然不会影响控制点坐标的平面精度,但会给垂直坐标精度带来巨大的误差。相较于方法A 和方法B,由方法C 得到的控制点平面坐标和垂直坐标精度均较高,且方法C未采用声线跟踪计算换能器和应答器之间的几何距离,因此不需要采集声速剖面,进而简化了作业流程,这说明本文提出的顾及深度信息和平面坐标先验信息的海底控制点精密定位方法是有效的。③比较方法A 和方法C控制点垂直解的精度可以看出,2种方法的结果虽然处于同一量级,但是方法C 的结果略高于方法A。这是因为方法C中的模拟数据中加入了涌浪效果,顾及了涌浪对控制点深度测量的影响,而方法A 中并未考虑。

表1 不同定位方法下应答器坐标外符合精度Table 1 The external precision of transponder coordinates by using different positioning methods

4 结语

本文提出了顾及表层声速和平面坐标先验信息的海底控制点三维坐标定位方法,将压力传感器测得的水深值视为新的观测量,并根据经验给定水深值的先验方差,同时考虑到声速误差仅对垂直坐标有影响,顾及控制点平面坐标的先验信息,采用广义最小二乘原理进行解算海底待求控制点的三维坐标。对于需要使用声速剖面进行声线跟踪的传统三维约束平差方法起到一定的补充作用,有助于在深远海等不易频繁开展声速测量的情况下开展应用,能够解决控制点三维坐标解算复杂的问题,并可极大节省测量成本,提高作业效率。在仅利用表层声速的条件下,通过开展模拟实验,得到了与利用声速剖面的三维约束平差方法同精度的定位结果,实现了海底控制点三维坐标的高精度获取,结果稳健可靠,表明此方法有很好的适用性。