基于趋势项距平值迭进式方差控制的SBE9plus CTD奇异值剔除方法

于 龙 ，孙 佳，熊学军*，郭延良

(1.自然资源部 第一海洋研究所,山东 青岛 266061；2.自然资源部 海洋环境科学与数值模拟重点实验室,山东 青岛 266061；3.山东省海洋环境科学与数值模拟重点实验室,山东 青岛 266061；4.青岛海洋科学与技术试点国家实验室 区域海洋动力学与数值模拟功能实验室,山东 青岛 266237)

现场调查是认知和把握海洋环境最直接、最有效的方法,为了能准确地揭示海洋环境的时空分布特征和变化规律,保证所获取调查数据的准确性和可靠性就显得尤为重要。目前观测方式和观测仪器多种多样,数据处理日趋自动化。然而,在调查现场,由于仪器或人为因素所产生的测量误差在所难免,主要包括随机误差和过失误差[1-3]。这就要求数据的后期处理人员对数据获取情况有足够了解,包括数据来源、现场调查环境等,在进行数据处理之前,根据现场情况对数据进行质量审查和控制,做出切合实际的判断,保留下那些能反应海洋环境异常变化的数据,去掉因误差造成的奇异值,尽最大可能还原现场海洋环境。

目前,对SBE9plus CTD(美国SEA-BIRD 公司生产的温、盐、深测量系统)剖面观测资料的处理,基本按照仪器自带的SBE Data Processing处理软件的流程进行[4-6],主要步骤包括低通滤波(Filter)、滞后订正(Align CTD)、热效应订正(Cell Thermal Mass)、消除逆压(Loop Edit)、奇异值剔除(Wild Edit与Window Filter)及衍生计算(Derive)等。其中,低通滤波对压力数据进行平滑,为后续消除逆压数据做准备；滞后订正目前多通过SBE11甲板单元实现[2,4],并在原始数据头文件中给出订正说明；对于热效应订正,可以采用Lueck[7]和Morison等[8]提供的校正系数对电导率进行热效应校正。通过低通滤波-滞后订正-热效应订正-消除逆压这4个步骤,可有效去除因各传感器不同步造成的数据“尖峰”及船舶起伏造成的数据“打结”。但在进行奇异值剔除时笔者发现,SBE Data Processing软件中的Wild Edit与Window Filter程序需要数据处理人员根据经验进行多次尝试[4,9],处理结果受人为因素影响较大,或条件过松无法尽除奇异值,或条件过严造成正常数据失真。此外,亦可采用中位数滤波结合最大偏差(Max Difference,MDIF)[10]或中位数绝对偏差(Mean Absolute Deviation,MAD)[11]进行奇异值剔除。其中,中位数滤波结合最大偏差法剔除效果较好,但其剔除结果取决于处理者对MDIF或最大梯度选择的合适程度,而MDIF随调查海区的不同而变化。若无法有效剔除温度、电导率等直接观测要素中的奇异值,则盐度、密度等导出量的数据质量更无从谈起。为此,本文对温度、电导率等直接观测量的奇异值剔除进行讨论。

首先明确奇异值的定义。每一个物理量均客观存在,其测量值分为真值、误差限内值和超出误差限值。绝对真实值无法通过测量得到,只能通过提高测量仪器的测量精度、减少环境因素和人为因素所造成的误差等,将测量值控制在误差限内,进而无限逼近其绝对真实值；而超出误差限值的数据则被认为无效数据,即奇异值。其特征如下:①物理上违背了观测值分布的基本规律和趋势,超出了观测对象的物理性范畴；②由于海水连续性特征,温度、盐度和密度等大多数物理海洋要素在时间与空间分布上的变化趋势,表现在曲线上应基本呈平滑状态,而奇异值在数学上违背了数据连续性法则,表现在曲线上即与曲线平滑性显著冲突；③仪器性能上表现在传感器的物理偏差、反应时间滞后及各传感器之间未能达到同步性调整等,从而造成“尖峰”等突变现象。

本文以SBE9plus CTD 剖面数据为例,提出了一种基于趋势项距平值迭进式方差控制的奇异值剔除方法。此方法主要参数涉及观测仪器采样频率与下放速度,可为其他型号CTD 剖面数据的奇异值剔除提供参考。

1 资料与方法

1.1 资料介绍

原始数据是以船载观测方式观测得到的多个站点的温、盐、深单点剖面资料,其中实例数据D1如图1所示。观测仪器为SBE9plus CTD 温盐深测量系统,采样频率24 Hz,其温度传感器分辨率为0.000 2 ℃,准确度为0.001 ℃；电导率传感器分辨率为0.000 4 mS/cm,准确度为0.003 mS/cm；压力传感器分辨率为0.068 95 dbar(0.001%FS),准确度为1.034 dbar(0.015%FS)。由于SBE9plus CTD 温、盐、深测量系统的压力传感器输出单位为dbar,为方便表述以及与仪器自带软件处理结果进行比较,我们在后续分析中仍然用dbar作为压力单位,而不使用压力的国际标准单位Pa,其换算关系为1 dabr＝104Pa。

如图1所示,原始剖面数据中温度和电导率均存在逆压数据,经过消除逆压(Loop Edit)后,仅电导率存在明显奇异值(图2)。观测甲板单元在现场观测时已对电导率传感器进行了滞后订正(Align CTD)0.073 s,因此在数据处理过程中对仅对电导率进行热效应订正(Cell Thermal Mass)。但在采用Wild Edit与Window Filter程序进行奇异值剔除时,需经多次尝试,且最终剔除结果或因条件过松无法尽除奇异值,或因条件过严造成正常数据失真。

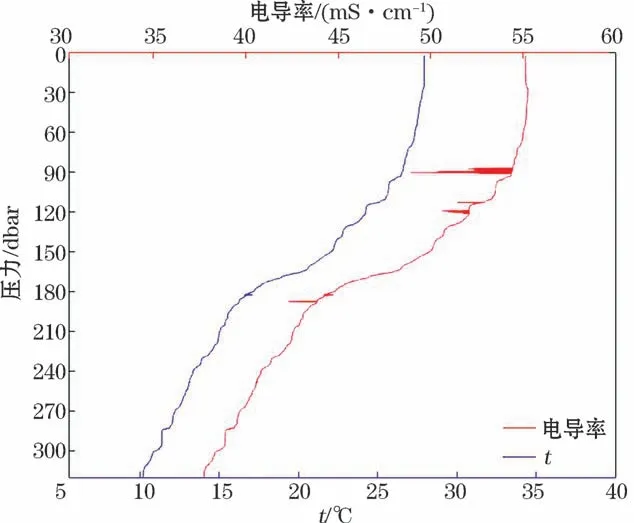
图1 CTD 原始数据D1Fig.1 The CTD raw data at D1

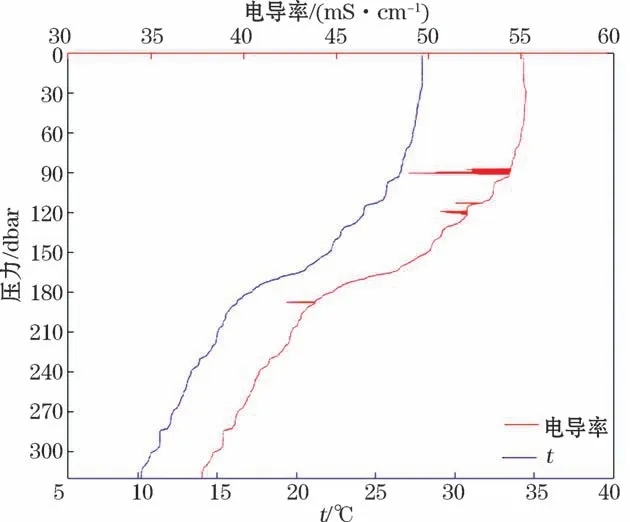
图2 消除逆压后CTD 数据Fig.2 The CTD data after Loop Edit

1.2 研究方法

由于原始数据在整个剖面上变化范围较大,特别是在温盐数据本身的变化幅度与奇异值导致的变化幅度之间存在交叉的跃层区或逆跃层区等海洋环境变化剧烈的水层,因此很难直接提出有效的奇异值判别条件,但奇异值具有震荡性,而跃层区与逆跃层区正常数据具有单调性。

针对以上区别,首先通过EMD(Empirical Mode Decomposition)方法[12]求取原始数据的最优趋势项,进而与原始数据做差求得距平,以距平为切入点进行奇异值的判别与剔除。具体步骤如下:

1)求取最优趋势项与距平

在求取趋势项时本文采用EMD 方法[12],该方法对非线性、非平稳过程数据进行距平化效果显著。通过EMD 方法得到的残余项本身就是趋势项,并且,还可以根据物理背景的不同,调整残余项与部分模态分量相加作为趋势项[13]。为了使趋势项尽可能地反映原始数据的所有信息,本文以王金良和李宗军提出的最小方差比率[14](后n项模态分量和的方差与原始数据方差的比)作为最优趋势项的判别条件。

2)识别奇异值区

根据数据采样频率F和观测仪器移动速度V,确定每k＝min(F/V)个数据作为一个区块,对距平A进行分割,得到一系列距平区块A n(j)(其中j＝1,2,3,…,k,代表每个距平区块内的数据量,max(j)＝k；n为距平区块个数,n＝1,2,3,…,max(n)＝[max(i)/k],i为原始数据的下标),若无法整分,取A中的最后k个数据作为最后一个距平区块,保证每个区块包含k个数据；然后求出每个距平区块的方差V n。由于这一步仅为寻找可能存在奇异值的区域,因此可以缩小方差控制区间,放宽判别条件,即对距平区块方差通过1倍方差控制识别奇异值区。本文所用资料的观测仪器采样频率为24 Hz,观测仪器下放速度在1.0～2.0 m/s,故取k＝12,使得区块的深度变化范围在1 m 之内。对于1 Hz等低频采样频率型号的CTD,可尝试直接进行数学分割或采用其他方法,但识别效果有待进一步研究。

3)剔除奇异值

奇异值区内的数据并不一定全部为奇异值,因此并不对上一步识别出的奇异值区进行整体方差控制,而是针对识别出的每个奇异值区Qm进行逐点判别。在判别第一个奇异值区内的第一个数据点时,由于其前面的数据可以确定为非奇异值,其后面的数据则暂时无法判定,因此取与其相邻的至少前2k－1个正常数据共同组成至少2k个数据量的被判别区,保证被判别区内的数据量至少为每个区块数据量的2倍。由于这一步需要识别出真正的奇异值对其进行剔除,从而扩大方差控制区间,加严判别条件,谨防误判,因此进行3倍方差控制。针对识别出的奇异值,在保证上升过程数据趋势与下降过程数据趋势基本一致且对上升过程数据质量有把控的前提下,取上升过程对应水层正常数据予以平移替代。在第一个数据点被纠正后可作为下一个被判别点的正常引入数据点,依次逐点推进,最终剔除整个剖面数据奇异值。

2 方法应用

以数据D1(图1)进行方法说明,在应用本方法之前对原始数据进行初步质量控制,包括去除感温数据、逆压数据及明显不符合常识的数据等,上述初步质量控制步骤完全可以通过编程实现自动化处理[15]。

第一步,采用EMD 方法求取最优趋势项。如图3a所示,当模态分量个数为9时,方差比率最小。即后9项模态分量的和为最优趋势项(图3b中红色实线)。将最优趋势项与原始数据做差得到距平(图3c)。

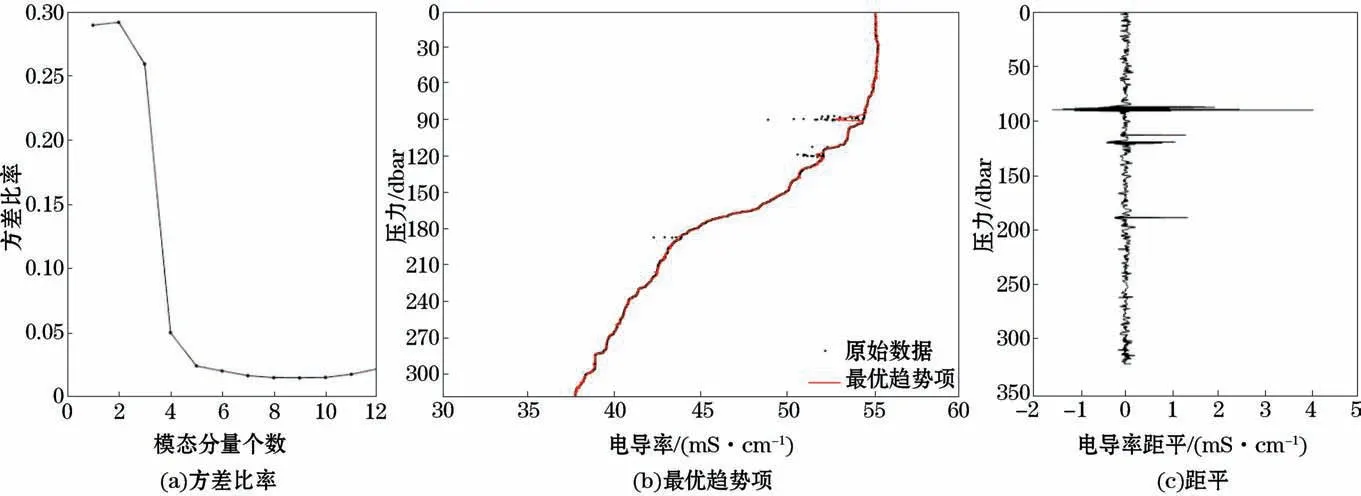
图3 方差比率、最优趋势项及距平Fig.3 Variance ratio,optimal trend and anomalies

第二步,识别奇异值区。将第一步得到的距平按照每12个数据一个区块进行分割,并求取每个区块的方差,然后对距平区块方差通过1倍方差控制识别奇异值区。数据的4个奇异值区如图4所示,依次与原始数据(图1红线)中从上到下的4个“尖峰”相对应。可以看到,原始数据中的4个奇异值区全部被识别。

第三步,剔除奇异值。针对识别出的奇异值(图4黑色圆圈),在保证上升过程数据趋势与下降过程数据趋势基本一致,且对上升过程数据质量有把控的前提下,取上升过程对应水层正常数据予以平移替代(图4红色实点)。在第一个数据点被纠正后可作为下一个被判别点的正常引入数据点,依次逐点推进,最终剔除整个剖面数据奇异值。最终结果如图5所示,在不改变其他正常数据的前提下,对奇异值进行了精准识别与靶向剔除。

图4 奇异值区、奇异值及使用同水层上升数据平移替代结果Fig.4 The identification results of abnormal block,abnormal data and their replacement with upcast data

图5 电导率原始数据、奇异值剔除结果、趋势项距平值及距平区块方差Fig.5 The raw data,elimination result,trend anomaly and variances of blocks

3 方法对比

在数据D1(图1)的基础上,增加另外6个同样存在奇异值的CTD 剖面数据实例(图6),分别使用本文提出的距平迭进方差法、SBE Data Processing中的Wild Edit与Window Filter方法以及中位数滤波结合最大偏差法共四种方法进行处理和对比分析,结果如下:

①采用本文提出的距平迭进方差法,处理过程无需针对每个实例进行个性参数设置,可对所有实例进行批处理,均可对所有实例中的奇异值进行靶向剔除,原始数据如图6黑点及图7a所示,剔除结果如图6红点及图7b所示。

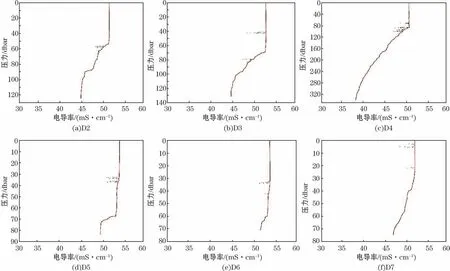
图6 CTD 原始数据(黑点)及本方法剔除结果(红点)Fig.6 The CTD raw data(black dot)and eliminate results(red dot)

②利用SBE Data Processing处理软件,首先对原始数据进行初步质量控制,去除感温数据及明显异常数据,然后依次执行Filter-Cell Thermal Mass-Loop Edit,采用2倍方差与4倍方差控制,从100～500不断改变区块大小多次运行Wild Edit[4]。但处理后数据D3～D7五个实例中仍存在明显奇异值,且继续多次改变区块大小运行Wild Edit后,剔除效果再无增益,数据D1剔除结果如图7c所示。

③执行SBE Data Processing-Window Filter-Median程序,剔除效果随滤波窗口大小的不同而存在差异,对于数据D1,与中位数滤波结合MDIF方法窗口保持一致取25时,无法剔除奇异值,如图7d所示。若窗口取为60,剔除效果稍有改善。此方法对其他正常数据同样进行了滤波处理,对正常数据改变较大。

④采用中位数滤波结合MDIF进行奇异值剔除时,首先计算7个实例原始数据的偏差情况,对整体偏差进行评估。由于7个CTD 剖面资料所处海域不同,最大偏差的选取也有所差异。对于数据D1,选取最大偏差MDIF＝0.05 mS·cm－1(图8中灰色实线所示)进行奇异值剔除,结果如图7e所示。

图7 奇异值剔除方法比较Fig.7 Comparison of the methods of eliminating abnormal data

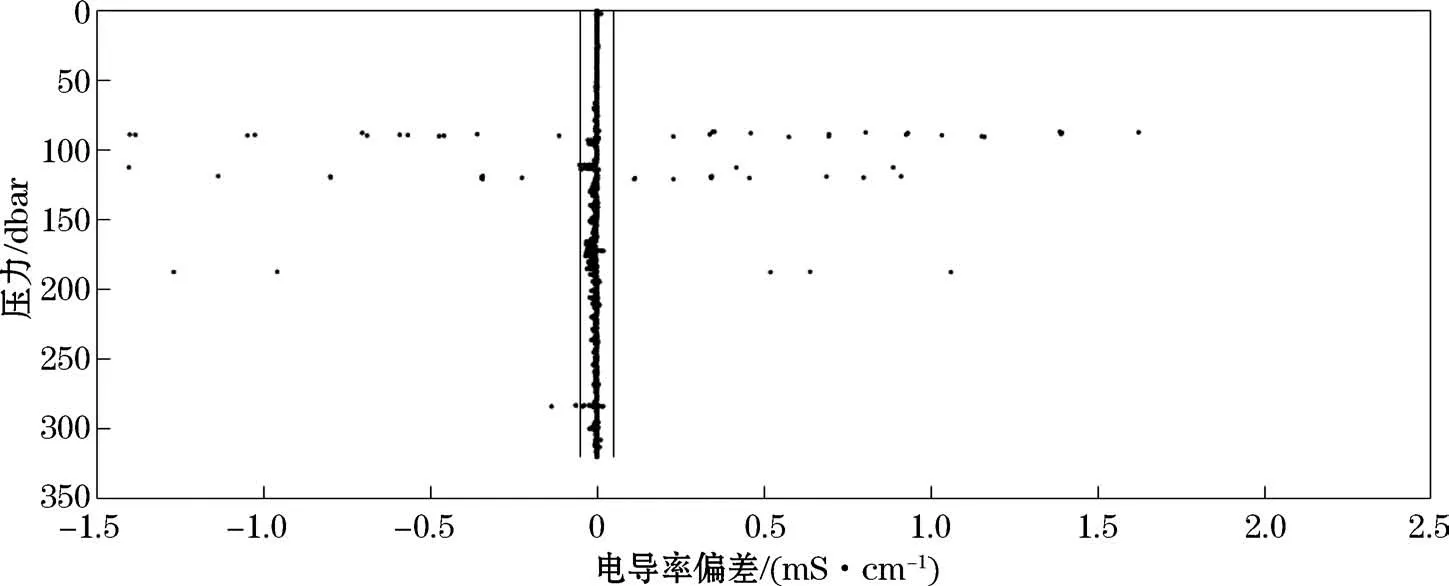
图8 电导率偏差Fig.8 Conductivity differences

为了进一步比较4种方法对正常数据的影响,将原始数据中的正常数据与结果中的相应数据做差,结果如表1所示,距平跌进方差法对所有实例的正常数据均无改变；中位数滤波结合MDIF法对数据D1、数据D2、数据D5、数据D7 无改变,但对数据D3、数据D4、数据D6 正常数据的改变较大,最大改变量达0.33 mS·cm－1；SBE Data Processing处理软件中的Wild Edit程序和Window Filter程序对所有实例的原始数据均有改变,最大改变量同样达到0.33 mS·cm－1。

表1 正常数据改变量统计(mS·cm-1)Table 1 Statistics of the change of normal data(mS·cm－1)

综上所述,SBE Data Drocessing处理软件中的Wild Edit程序与Window Filter程序在处理过程中需要多次尝试,处理效果具有不确定性,且对其他正常数据的改变较大；中位数滤波结合MDIF法剔除效果优于前面2种方法,但同样存在改变其他正常数据的情况,且需根据不同剖面数据选取合适的MDIF；本文提出的距平迭进方差法可实现对异常值的精确识别与靶向剔除,避免多次尝试、误判以及处理结果的不确定性等,对高频采样频率的CTD 剖面数据的异常值剔除具有普适性。

4 结语

本文针对SBE9plus CTD 剖面数据的奇异值剔除问题,基于多个CTD 剖面数据实例,提出了一种利用趋势项距平值迭进式方差识别CTD 剖面数据奇异值的方法。首先通过EMD 方法求取最优趋势项进而得到距平,通过方差控制识别出奇异值区,在奇异值区内逐点推进,再次通过方差控制识别奇异值。并与SBE Data Processing软件中的Wild Edit程序和Window Filter程序,以及中位数滤波结合最大偏差法进行了比较分析。实例应用与方法对比结果表明,本文提出的基于趋势项距平值迭进式方差控制的奇异值剔除方法具有以下特点:

①可以对奇异值进行精准识别与靶向剔除,对奇异值的剔除更有针对性,且不会改变原始数据中的正常数据,最大程度保留数据原始特性；

②可以一次性尽除奇异值,避免不断改变判别阈值进行多次尝试,避免因人为因素选择不同的判别阈值而导致不同的剔除结果；

③该方法适用于其他高频采样频率的CTD 剖面数据,对于1 Hz等低频采样频率的CTD 剖面数据,其适用性有待进一步探讨。