内河水下边坡稳定性及加固方案研究

刘振楠

（中铁十八局集团北方区域指挥部，北京 100048）

在内河水域进行水下基槽开挖时，必然涉及到水下边坡的稳定问题.水下基槽开挖扰动将使土体密实度变小、孔隙率增大、渗透性增强、土体抗剪强度参数普遍降低.当基槽边坡土体内部下滑力超过抗剪强度时，坡体就会产生塑形变形，进而导致边坡失稳.此外，浚挖后基槽内极可能发生泥沙回淤，增加边坡荷载，且回淤土强度极低、土质松散且稳定性差，亦会对基槽稳定造成不利影响.因此，在水下基槽开挖中，必须充分考虑开挖过程土体强度的衰减以及回淤土对边坡的稳定性影响，并采取针对性的加固措施，以保证基槽边坡的安全[1].

近年来随着我国基础设施建设投入加大，内河隧道工程逐渐增多，研究人员对水下基槽开挖稳定性也有了更多认识.贺少辉等[2]对京沪高铁南京长江沉管隧道水下砂质边坡稳定性进行了研究，提出“水下边坡的初始破坏发生在坡脚”的结论，这与“水上边坡通常先由坡顶发生开裂，之后开始滑移”的通常认识不同；王晨希等[3]考虑河道冲刷的影响，进行了坡底高程和坡度对水下边坡稳定性影响的回归分析；周顺华等[4]、林枫等[1]分别研究了渗流情况下的水下边坡稳定性问题，认为在内河水流速度较小时，渗流会有利于水下边坡的稳定，而河流平均流速低于1 m/s 时，不需考虑水流在基槽中产生的低压区和高压区；潘家铮[5]提出当边坡完全淹没水中，此时计算下滑力和抗滑力时土体的重度指标都应采用浮重度；詹信群[6]以广州某沉管隧道工程为背景，基于有限元，建立了关键施工过程中沉管管段和基槽模型的空间力学分析模型，论证了有关施工的合理性和安全性；程栋栋等[7]对水下基槽边坡土体在卸荷状态下的承载与变形特性进行了研究，并对基槽的稳定性和安全系数进行了分析；赖金星等[8]以福州市湖东东路水底明挖隧道基坑为工程依托，对水下基坑开挖过程中的周围土层和支护结构的受力变形规律进行了分析；张建新等[9]结合现场监测资料，研究了回淤现象对沉管隧道水下基槽边坡的稳定性的影响，并提出了合理坡率. 国外方面，Kosyan 等[10]针对内河河道水下天然边坡进行了长达7 a的连续观测，得到了水下边坡不同位置变形量和变形速率的相关规律.

目前对水下基槽边坡研究主要基于边坡稳定性理论，以极限平衡原理为基础进行分析[11-13].针对水下边坡稳定的系统性研究成果极其不足[1]，同时，水下边坡加固方面的文献多限于施工，而加固机理、加固技术参数等理论方面的探讨还不够深入.

本文针对天津海河隧道水下基槽浚挖工程，采用有限差分法建立了水下边坡钻孔灌注桩加固三维分析模型，对非加固和不同加固参数等多种工况下的水下边坡稳定性进行分析，同时，对加固中主要施工参数对边坡稳定性影响程度进行讨论和评估，研究成果对内河水下基槽浚挖工程的安全施工具有重要的工程实践意义.

1 工程概况

本文研究基于天津海河隧道水下基槽开挖工程.基槽所在河段河床地质条件变化不大，均为淤泥质软土，呈灰色、饱和、软塑，土质均匀，自河床底部向下分布较厚的黏土和粉质黏土.水文方面，该段河道呈长条形，流速不超过0.5 m/s，非汛期水位控制在0.89～0.78 m 左右.由于河床多年未进行清淤工作，淤泥层厚，基槽边坡稳定性差，加之水下作业可视性低，故工程可能面临较高风险.

基槽开挖位置原水深约为6~8 m，基槽尺寸为56 m×72 m，位置如图1 所示.基槽开挖土层深度8 m，依设计要求，采用分层开挖方式，分4 层进行，每层土体开挖厚度约为2 m. 基槽浚挖面底标高为-14.106～-17.087m，边坡南北方向按1 ∶2 设置，东西方向按1 ∶3 设置，上下两层边坡高度均为4 m，中间设1 级平台，平台宽2 m，基槽开挖剖面如图2 所示.

图1 基槽位置示意

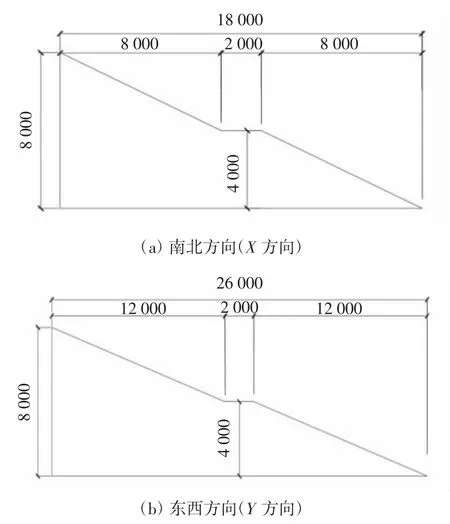
图2 开挖剖面示意

2 水下边坡稳定性有限差分分析模型

结合实际工况，采用FLAC3D 分析软件，建立三维数值分析模型，对分步开挖状态下水下边坡的稳定性进行研究.通过计算不同工况下基槽边坡各个位置的应力、位移、变形速率等参数，综合分析影响水下基槽边坡稳定性的各种因素，探求水下边坡失稳的主要影响因素及破坏发生的区域位置.

2.1 本构模型和几何尺寸的确定

参照国内外研究经验[1，3]，当水体流速较慢（流速小于1 m/s）时，土体渗流作用有利于水下边坡稳定，从工程安全和计算效率角度考虑，本工程数值分析时忽略水下边坡土体的渗流问题.土体强度参数采用固结快剪指标，本构模型选用了Mohr-coulomb 弹塑性模型，不排水材料类型，网格单元选用8 节点六面体单元.钻孔灌注桩桩体选用线弹性桩体模型Pile 单元.根据工程实际情况，选取了最不利的断面位置进行建模.

结合实际开挖情况，基槽顶部位于水面以下6 m，开挖深度约为水下14 m.根据对称原则，选取1/4 基坑进行建模，同时考虑边界效应对计算结果的影响，将模型尺寸设定为48 m×66 m×38 m（长×宽×深），网格数为131 040 个.边坡分两阶斜坡，中间设2 m 的平台，X 方向坡度 1 ∶2，Y 方向坡度 1 ∶3.

2.2 初始边界条件和计算参数

现场开挖深度为6 m，上表面作用静水荷载为60 kPa.水平方向边界施加位移约束，竖向模型底面边界施加位移约束，上表面为自由面.

计算时，水下边坡土层按4 层进行简化，第一层厚度3.5 m；第二层厚度5.5 m；第三层厚度10 m；第四层为基槽底部土层，厚度19 m.土层及桩体参数如表1 所列.

表1 土体及桩体参数

3 水下边坡稳定性分析

计算时假设[13-14]：①忽略边坡土体内部的应力集中对计算结果的影响；②达到极限平衡状态的土体仅在边坡滑动面上；③边坡土体与桩之间无相对滑动.

3.1 无支护条件开挖过程边坡稳定性

现场试开挖监测资料显示，开挖后基槽表层土体强度遭受明显破坏，各项强度指标下降幅度高达20%，同时边坡表层各位置均产生回淤，边坡外形变化处回淤量最大.基于此，本文在开挖完成后，对表层土体强度参数进行适当折减，同时施加回淤荷载，结合现场开挖试验槽的回淤量监测数据，本文将回淤土对水下边坡的影响简化为施加于边坡表层位置的附加竖向荷载（通过试验槽监测值估算，取最大回淤位置的竖向荷载值，约为11.2 kPa），之后对开挖全过程中边坡土体的应力、位移、加速度等参量进行计算分析.开挖分析模型如图3 所示.

图3 开挖区域示意

计算分析结果见图4 和图5.可见，未支护加固时，边坡会产生较大变形.坡度对边坡的稳定性存在一定影响，但坡度差别不大时，影响程度有限（1 ∶2 坡率边坡最大位移75 mm，安全系数FS=1.206 6；1 ∶3坡率边坡最大位移71 mm，安全系数FS=1.253 9）.

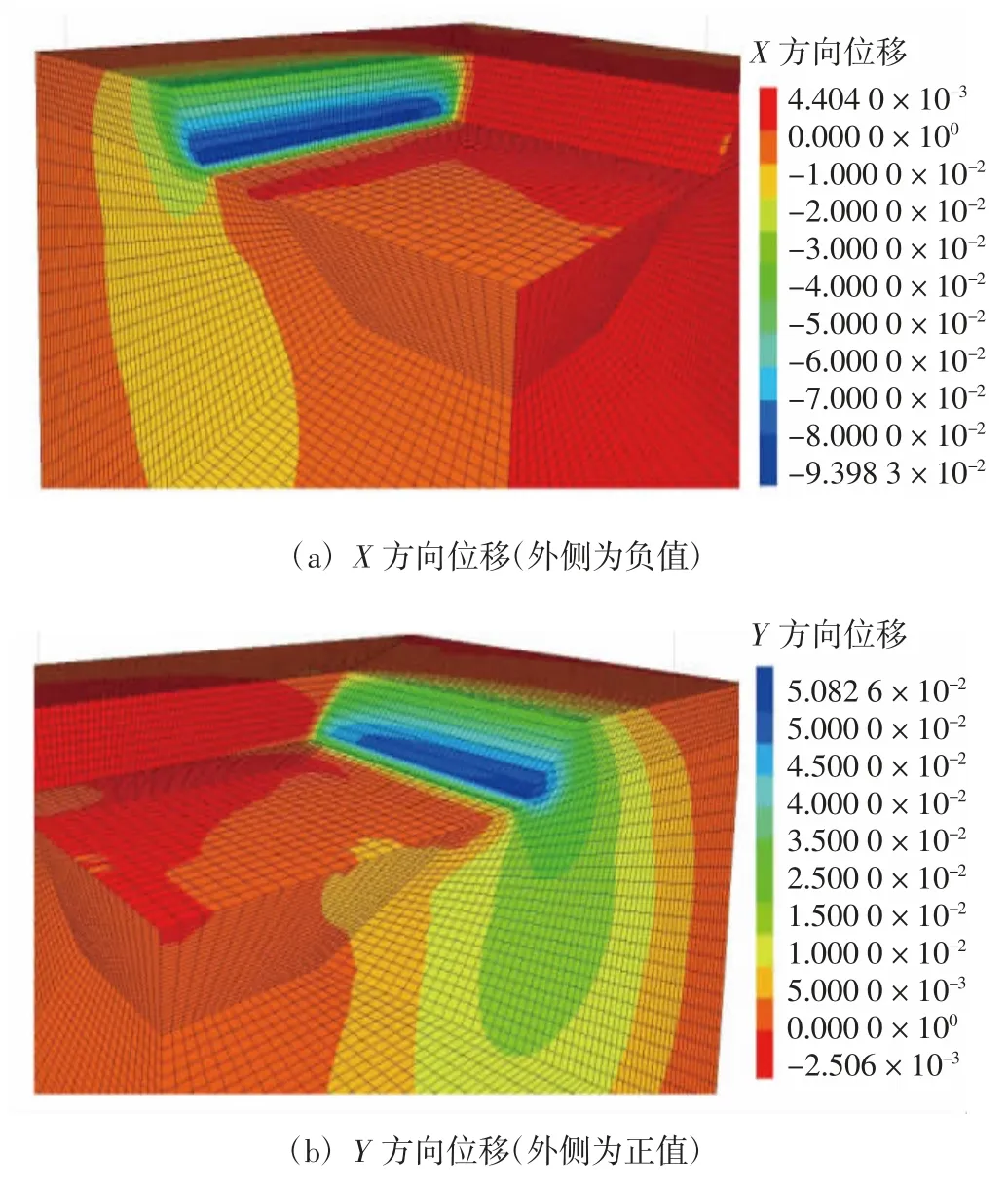
图4 上层开挖后位移云图

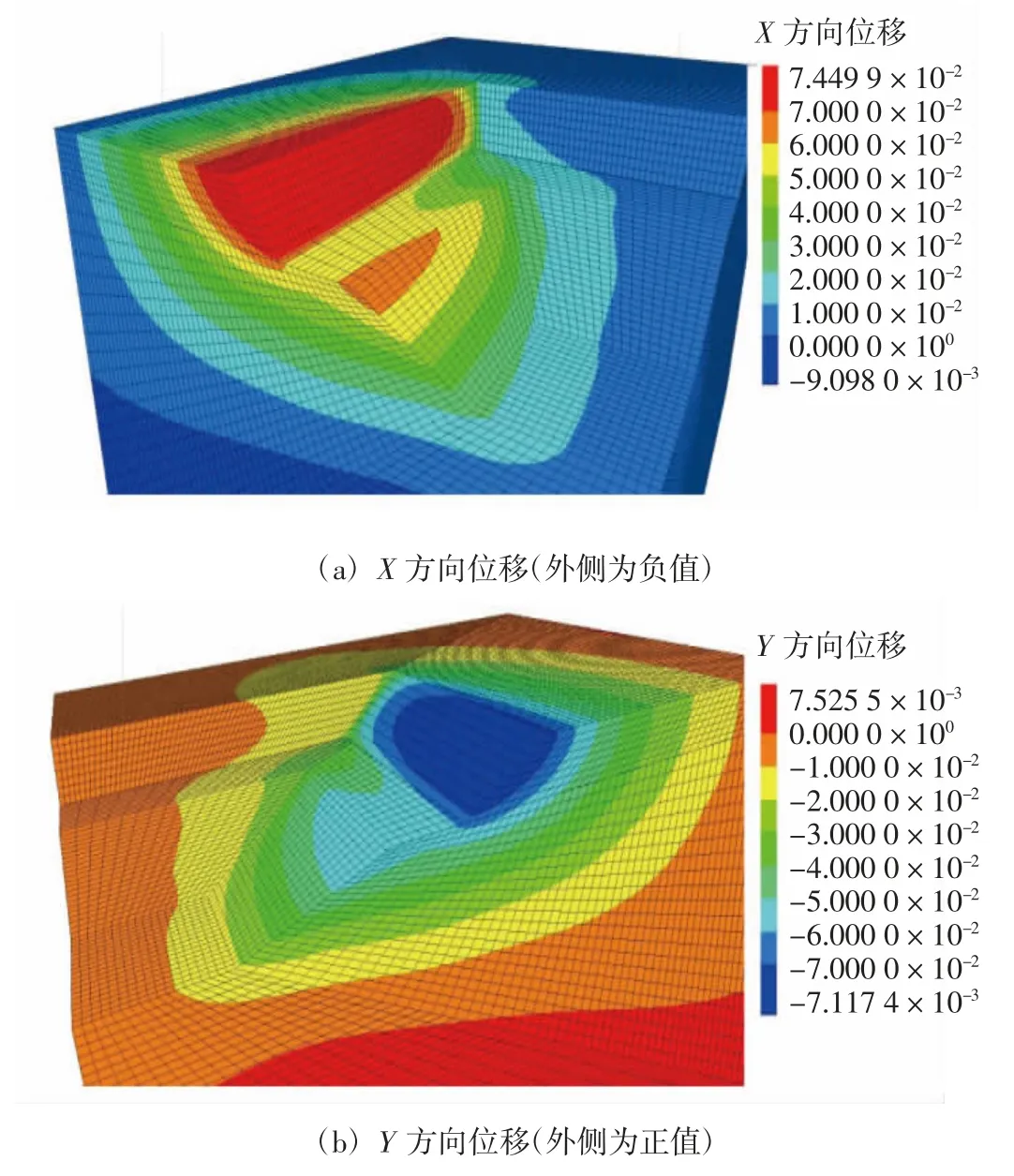
图5 下层开挖后位移云图

在未支护条件下，水下边坡开挖过程中上层坡脚位置和中央平台边缘的土体变形值较大，这与开挖试验中对基槽底部土体的水下地形测量结果一致.分析认为：该位置接近河床，土体为低强度的淤泥质土，转角处应力集中现象也使这些位置位移增大. 同时，分析还表明，开挖扰动对水下边坡的稳定性影响明显，一方面，开挖造成的土体强度损失会增加基槽的竖向和水平位移；另一方面，开挖后河床回淤会使边坡上竖向荷载有所增加，在两者的共同影响下，边坡的稳定性显著降低.

3.2 水下边坡经典算法比较

在前述数值分析基础上，本文借鉴文献[1]中基于经典条分原理的积分算法对水下边坡稳定性进行对比分析.

在水下边坡取一单元土条，根据其自重W、滑动土体渗透压力Fd和滑动面上的抗滑力T 之间的受力平衡，列出平衡方程式

式中：N 为潜在滑动面上的法向压力；c 为土体黏聚力；φ 为土体内摩擦角；β 为滑动圆弧切线方向与水平面的夹角；L 为潜在滑动弧长.

安全系数K 为抗滑力矩与下滑力矩的比值，计算公式如下

式中：R 为潜在滑动圆弧半径；M 为渗透力力矩；G 为条形土体单元总下滑力.

本文按 1 ∶2 和 1 ∶3 两种坡率分别进行计算，计算结果与数值分析结果对比见表2.

表2 经典计算法与数值分析法安全系数比较

对于出现计算差异的原因，本文认为：经典计算方法基于土体的极限平衡条件，以受力平衡作为是否破坏的评判标准；而数值分析的计算原理是强度折减法，破坏判断依据是边坡内达到临界失稳状态的塑性区范围.对于水下边坡的稳定性问题，后者对土体参数变化更加敏感，故本问题中数值分析得到的安全系数偏小.但是由表2 可知，采用两种方法计算得出的安全系数相差不到10%，且计算结果均表明边坡处于稳定状态.因此，本文对水下边坡进行稳定性分析结论是合理的，工程上具有可行性.

4 灌注桩加固水下边坡稳定性分析

参考国内外工程[15-17]，采用钻孔灌注桩作为抗滑桩对边坡加固经验丰富，效果良好.本工程采用钻孔灌注桩对水下边坡进行加固.基于上节研究结果，理论上加固位置宜选择变形最大区域，即上层边坡坡脚位置和中间平台边缘，但从钻孔灌注桩施工场地要求考虑，最终选择在下层边坡坡脚处设置桩体进行加固.桩体设置见图6 所示.

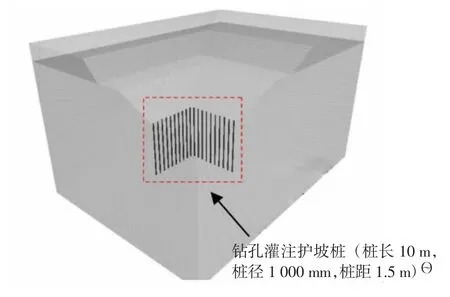
图6 加固桩设置示意（工况一）

对采用灌注桩护坡加固前后其边坡变形情况进行分析，加固桩直径1 m，嵌固深度10 m，桩距1.5 m，计算结果见图7.可见，经灌注桩加固后水下边坡位移显著减小，东西向边坡未加固时最大位移7.12 cm，加固后最大位移4.65 cm；南北向边坡未加固时最大位移7.45 cm，加固后最大位移5.47 cm.坡体各位置位移平均减少近30%.这说明坡脚位置采用灌注桩护坡可明显减小坡体变形，提高水下边坡的稳定性.

图7 桩加固后边坡开挖后位移云图

基于灌注桩良好的加固效果，进一步对灌注桩桩距、桩径和桩埋深等参数对水下边坡稳定性的影响进行分析.为比较各施工参数的加固效果，设定了多种工况模式，具体工况和计算分析结果列于表3.

表3 不同工况下水下边坡的位移值和安全系数

工况一、二、三对比分析. 计算结果表明，边坡安全系数随灌注桩桩径增大而增加，由桩直径1 000 mm时的1.533 增加到直径1 500 mm 时的2.052，增加了约33.9%，而边坡最大水平位移由54.7 mm 减小至41.7 mm，减小了23.8%，边坡稳定性明显提高.由于桩径增大，使得桩体受力面积增大，桩身所承担的外荷载得以分担，而周边土体的应力影响较小，使得桩身变形减小，增加了对周边土体的约束，从而使安全系数提高.通常情况下，桩径越大，安全系数越高，两者的增长趋势比较一致.

工况二、四、五对比分析. 计算结果表明，边坡安全系数随桩间距增大而降低，由桩距1.5 m 时的1.987下降到间距2.4 m 时的1.449，下降约27.1%.这是由于随着桩间距的增加，坡脚位置处桩土间作用力将重新分配，呈现逐渐减小的趋势，而桩体对土的约束作用随之减小，边坡土体变形增大，稳定性降低，反之亦然.但是，随桩距持续减小，边坡稳定性增加幅度会降低直至停止，此时桩体对土的约束作用已接近极限.工程实践中，桩间距过小，施工中相邻桩体之间会产生相互扰动，且桩数量会明显增加，施工成本随之增加.

工况四、六、七对比分析. 计算结果表明，边坡安全系数随桩长增大而增加，由桩长10 m 时的1.639 增加到桩长18 m 时的2.419，增加了约47.6%，边坡最大位移由49.8 mm 减少至37.5 mm，减少幅度24.7%，可见边坡稳定性增长趋势明显.分析认为，由于桩长增加，桩侧摩阻力随着桩长增加而增大，桩对土的约束作用不断增强，起到了加固土体的作用.但相关研究表明，护坡桩的长度达到某限值时，桩对土的约束作用不再明显，之后长度增加并不会使边坡稳定性持续增强，桩长限值与边坡潜在滑动面的深度密切相关.

5 结 论

基于天津海河隧道水下基槽工程，对开挖过程中水下边坡的稳定性进行研究，得到如下结论：

（1）水下开挖引起的土体扰动及泥沙回淤将明显降低边坡稳定性，特别在河床表层及应力集中区域，边坡极易出现较大变形.建议在水下开挖施工前建立测量控制网，确定基槽开挖范围，浚挖后及时根据测量结果，调整工艺参数，优化施工方案，尤其是对坡脚和中间平台位置的土体应加强监测，并采取有效加固措施防止边坡坍塌.

（2）采用钻孔灌注桩加固边坡，可有效限制水下边坡的侧向变形.加固桩桩长对边坡稳定性的影响明显，桩长越长，安全系数越高，但存在一定界限长度，同时，桩径、桩距对边坡稳定性也有一定影响，桩径越大，桩距越小，边坡稳定性越高.

（3）结合本文工程，建议水下加固边坡时应首先考虑桩长对边坡稳定性的影响，将桩长尽量插入边坡潜在滑动面以下一定深度（宜大于10 m），同时要考虑水下开挖扰动和回淤的不利因素，保证足够安全余量.基于施工便利性和经济性，本文建议海河水下边坡加固可采用14 m 桩长、1 200 mm 桩径和2 m 桩距的灌注桩加固，计算边坡安全系数宜达到2.2 以上.