迈克尔逊干涉仪的仿真研究

摘要：近些年来，随着计算机科学的发展，人们发现可以利用计算机语言来对光强公式编写，然后利用计算机模拟出干涉图样。本文首先分析迈克尔逊干涉仪中等倾干涉原理，然后应用MATLAB计算机软件基于各原理编写程序，模拟了各干涉条纹图样。方便地反映出入射光的波长、介质折射率等各参数与条纹图样的关系。用直观的图像将复杂的理论形象化，使学习者对迈克尔逊干涉的性质、理论以及规律更加清晰明了;更能丰富教师的教学资源。

关键词：等倾干涉;迈克尔逊干涉仪;MATLAB模拟

物理学的实验性很强，实验是研究物理知识必不可缺的重要组成部分。但人们很难把握有些实验的实验条件，稍有不慎就会使整个实验全军覆没。随着科学的发展和科技的进步，计算机的问世帮助人们解决了很多的难题。19世纪后期有位科学家叫迈克尔逊，他和他的同伴莫雷经过不懈的努力设计出一种利用分振幅法实现干涉的仪器——迈克尔逊干涉仪。它出现推动了物理学史的发展，至今在现代科技上仍起着非常重要的作用。但是实验者在做迈克尔逊干涉仪实验时发现，不仅它的原理复杂和抽象，而且对其实验环境和调节技巧具有较高的要求，否则很难得到理想的实验结论。本文首先分析迈克尔逊干涉仪的实验原理，以及产生等倾干涉条纹的条件，然后在此基础上用MATLAB编写程序，并对此进行仿真研究。这样就可以不受仪器、环境以及繁琐的调节技巧的影响，从而得到理想的实验效果。

1 迈克尔逊干涉仪

1.1迈克尔逊干涉仪装置原理

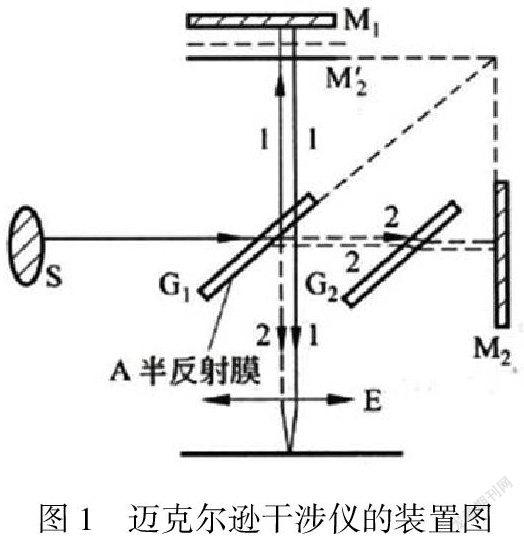
扩展光源S发出一束光，这束光首先照射在玻璃板G1板上，因为它的下表面被涂有一层半反射半透明的膜，所以这束光就会被它分成两部分，且这两部分光强度，频率，相位差都相同。（为便于表达本文把经G1反射出的光稱为光线1，把经G1透射出的光称为光线2。）其中，光线1又射向位于G1上方并与G1成45°倾角的平面镜M1上，再经M1反射后透过G1射向汇聚透镜E，最后光线被汇聚在透镜的焦平面上。光线2经过位于G1右侧并于G1平行的且材质大小和G1都相同的玻璃板G2透射到平面镜M2上（M2是与M1相同的平面镜，且与M1相互垂直放置），又被M2反射后经原路返回到玻璃板G1处，再经G1上的半反射膜A反射到达E处，汇聚后到达焦平面上。其中，G2称为补偿板，用来补偿光线2的光程，这样两束光线就分别三次穿过玻璃板。所以最初被半反射膜分开的两部分光就又会相遇发生干涉现象。此原理装置图如图1所示。

1.2 迈克尔逊干涉仪与薄膜干涉的关系

其实平面镜M2经半反射膜A反射后会在与M1平行的位置成一虚像M2'，所以上述中汇聚的光可以看成是分别由平面镜M1和虚拟平面镜M2'反射后相遇的光。这样一来，就实现了在M1和M2'之间成功创造出一空气薄膜，可以等效为薄膜干涉即一束光照在薄膜表面，其中一部分被上表面反射，另一部分经下表面反射，最后相遇后发生干涉。

2 等倾干涉实验的原理和仿真

2.1 等倾干涉条纹产生的原理

当M1和M2严格垂直时，等效空气薄膜层的两个平面M1、M2'就严格平行。光源S发射出来的光经半反射膜分成两束光，这两束光分别又经各平面镜反射，最后两束光经半透膜汇聚后叠加形成干涉。此过程可以等效为以下光路图2所示，一束光以i的角度入射到等效空气薄膜的上表面，光的一部分直接发生反射，另一部分发生折射，经下表面反射，再由上表面折射后回到原来介质中。这两部分光通过透镜汇聚在屏幕上。

设入射角为i;空气薄膜层M1与M2'之间的厚度为d，则两束光的光程差为：

可见当空气薄膜层M1与M2'之间的厚度为d一定时，光程差取决于入射光的入射角i。因此，由平板反射的相同入射角i的光线形成的反射光在汇合点具有相同的光程差。也就是说，相同入射角i的所有入射光线都可以形成相同的干涉条纹。由于通过平板角度不同的光线反射形成的干涉条纹是几个同心圆的明暗光环，所以这种干涉条纹被称为等倾干涉条纹。

现在计算屏幕上任意一点的光程差。已知到达屏幕上的光是由光束1和光束2叠加而成的，设汇聚点距屏幕中心的距离为r，汇聚透镜的焦距为f，如图3所示。由几何光学的知识可知，光束S的入射角满足：

2.2 利用MATLAB仿真等倾干涉实验

基于上述原理分析，利用MATLAB软件进行仿真。设入射光的波长λ=589.3nm，入射角θ=0.15rad，M1和M2'之间的等效介质薄膜的厚度为d=0.2mm，介质折射率n=1，透镜焦距f=200mm。根据这些数据在MATLAB软件中编写可直接执行的程序，然后逐一改变上述参数，可以得到相应的迈克尔逊等倾干涉条纹图样。下面是迈克尔逊干涉仪中等倾干涉的MATLAB程序。

运行该程序可得到图4：

从图4中可以看出，干涉图样为一组黑白相间的同心圆环，同时可以看出越远离屏幕中心的圆环越密集，总体呈现出内疏外密的特点。以下将通过改变各个参数来观察对干涉条纹的影响。

2.2.1入射光的波长对干涉条纹图样的影响

入射光的波长不同，其运行得到的干涉条纹图样也不同。如下图5所示，图（a）图（b）图（c）分别是其入射波长λ为390nm、530nm、780nm的干涉图样。由观察可得，在相同区域内条纹的疏密程度随着入射光波长的变化而变化，且波长越长条纹宽度越宽，干涉条纹就越稀疏;波长越短条纹宽度越窄，干涉条纹越紧密。也就是说，在相同大小的平面空间内，可看见的级数随着入射光波长的增长而减少。

2.2.2 等效介质薄膜厚度对干涉条纹图样的影响

等效介质薄膜厚度不同，其运行得到的干涉条纹图样也不同。如下图6所示，图（a）图（b）图（c）分别是其薄膜厚度d为0.1mm、0.2mm、0.3mm的干涉图样。由观察可得，在相同区域内条纹的疏密程度随着薄膜厚度的变化而变化，且薄膜厚度越薄条纹宽度越宽，干涉条纹就越稀疏;薄膜厚度越厚条纹宽度越窄，干涉条纹就越紧密。也就是说，在相同大小的平面空间内，可看见的级数随着等效介质薄膜厚度的增加而增加。

2.2.3介质的折射率对条纹图样的影响

介质的折射率不同，其运行得到的干涉条纹图样也不同。如下图7所示，图（a）图（b）图（c）分别是其折射率n为1、1.33、1.65的干涉图样。由观察可得，在相同区域内条纹的疏密程度随着介质折射率的变化而变化，且折射率越小条纹宽度越宽，干涉条纹就越稀疏;折射率越大条纹宽度越窄，干涉条纹就越紧密。也就是说，在相同大小的平面空间内，可看见的级数随着介质折射率的增大而增大。且由观察可得干涉条纹的明暗对比度与介质折射率也有关系，折射率越小，条纹图样的对比度越低。

2.2.4 透镜焦距对干涉条纹图样的影响

透镜的焦距不同，其运行得到的干涉条纹图样也不同。如下图8所示，图（a）图（b）图（c）分别是其透镜焦距f为0.15mm、0.20mm、0.25mm的干涉图样。由观察可得，在相同区域内条纹的疏密程度随着透镜焦距的变化而变化，且透镜焦距越短条纹宽度越窄，干涉条纹就越紧密;透镜焦距越长条纹宽度越宽，干涉条纹就越稀疏。也就是说，在相同大小的平面空间内，可看见的级数随着透镜焦距的增长而减少。

结论

在研究薄膜干涉等实验时，我们利用MATLAB强大的绘图和计算功能，在不使用任何光学仪器的情况下，可以进行对迈克尔逊干涉仪中等倾干涉实验模拟在不同参数变化时的干涉图样，而且可以通过干涉图样的变化规律直观的验证了干涉理论的正确性。这对于干涉图样的研究具有一定的意义，并且可以使学生的学习以及教师的讲授这部分内容时从实验室中解放出来。可以采用计算机软件对各类实验进行模拟和仿真，通过改变各类参数得出结果，从而使学生把握规律。

参考文献：

[1]赵凯华，钟锡华.光学（上册）[M].北京：北京大学出版社，1982：172-176.

[2]姚启钧.光学教程（第五版）[M].北京：高等教育出版社，2014：33-44.

[3]曹卫军.基于Origin的迈克尔逊仪等倾干涉仿真研究[J].昌吉学院学报，2016（03）：95-99.

[4]乔亮.迈克尔逊干涉实验的仿真研究[J].重庆三峡学院学报，2015，31（03）：50-52.

[5]梁齐，许晓琳，王明虎.光干涉实验的计算机模拟[J].大学物理实验，2003，16（3）：61-63.

作者簡介：郭珍（1997—），女，汉族，山西孝义人，学历：2021级在读研究生（学号20212513003），单位：太原师范学院，研究方向：学科教学物理。