基于支持向量回归改进的工况传递路径分析方法及其应用

胡 涵，高 亮，孟 言，郑 辉

(1.上海交通大学 振动冲击噪声研究所，上海 200240；2.徐工集团徐工机械道路机械分公司，江苏 徐州 221004)

工程机械驾驶室的声学舒适性较差是制约国产工程机械市场占有率的重要因素之一。振动压路机作为一种主要的压实机械，振动作业的特性引发驾驶室板件和整机结构件的振动，进而引发整机的噪声与振动。振动通过结构传递路径传递至驾驶室，强烈的振动严重影响司机操作的舒适性，甚至会导致驾驶室地板断裂；同时，较大的钢轮激励力使得钢轮向外辐射较大噪声，并通过空气传递路径传入驾驶室，与驾驶室由于结构振动产生的结构噪声一起构成驾驶室内恶劣的声学环境，严重影响司机的身心健康。

噪声的控制可以从激励源、传递路径、接收者三个基本环节入手。对应的处理方法分别是减弱激励源的强度、对主要传递路径进行隔离和消振或噪声主动控制手段等。其中，从传递路径分析方法的改进入手，分析双钢轮振动压路机驾驶室内噪声的传递路径，辨识驾驶室内噪声的主要传递路径，并最终将所得结论应用于压路机的降噪设计，对于驾驶室的声学设计具有重要意义。

传递路径分析[1](transfer path analysis,TPA)作为一种基于试验的研究方法，能够根据试验获取的数据建立系统的“激励源-传递路径-接收者”模型，分析不同激励源对接收者响应的贡献，从而对传递路径的贡献量进行排序，识别出主要的传递路径，对后续减振降噪工作的开展提供重要依据。然而，传统的TPA方法要求对系统装配交界面处的自由度进行大量繁琐的频响函数测试，测试过程中还需要将主动部件拆除。这对于大型工程机械这类激励部件不易拆卸的复杂系统不具有可行性。

工况传递路径分析方法(operational transfer path analysis,OTPA)[2]只需测取运行工况下激励源附近结构响应的数据，作为激励力的代替输入建立模型，即可得到响应点处的路径贡献，省去了大量繁琐的传递函数测试，因而受到工业界的欢迎[3-4]。有研究表明[5]，尽管由于路径串扰、噪声等原因，运用OTPA方法进行分析时会损失精确度，但就找出主要路径贡献而言是有效的。

遗漏路径的辨识方法、消除或减弱信源交叉耦合的方法以及OTPA的工程应用是目前国内外对于OTPA方法的研究热点。Bianciardi等[6]对OTPA方法进行了信号源串扰实验，提出为保证分析结果可靠性，信号源不相干的工况数至少和输入数目相等。Asahina等[7]使用OTPA方法对有轨列车阻尼器到车内地板的振动传递路径进行了分析，分析了各个路径的相关系数来检验各路径信号的独立性，同时使用重相干函数检验了输入与输出之间的线性度，确认了无重要路径遗漏。付俊涵[8]对于OTPA方法中信号交叉耦合的现象进行了深入研究，应用完全Cholesky分解预处理与最小二乘法相结合的方式进行了对病态方程的有效求解，提出了消除声源串扰的方法。伍先俊等[9]提出为减小源之间的串扰传感器应布置在尽可能靠近激励源的位置。Cheng等[10]提出了基于Tikhonov正则化的OTPA方法，并给出了正则化参数λ的取值范围，经过试验验证提高了求解结果的拟合度和稳定性。然而，对于OTPA方法中降低噪声和串扰消除的各种方法实际效果的横向比较还少有研究。此外，由于OTPA方法中使用距离振源附近的测点测量值代替实际的激励力，不可避免地会在信号中引入噪声。随机噪声具有不确定性，因而使得分析结果具有不确定性。事实上，使用同次试验取得的不同数据建立的OTPA模型，其分析结果也会有所差别，尤其是当传递路径选取不当(即遗漏路径或包含不含振源的路径)，不同试验有可能会出现非常大的差异，构成对主要传递路径判断的干扰。因此，量化OTPA方法中的不确定性，提高主要路径贡献的置信度，对于拓展该方法在解决工程问题中的应用具有重要意义。

本文以大型工程机械为研究对象，面向其驾驶室降噪需求，应用支持向量回归(support vector regression,SVR)理论和工况传递路径分析原理，并结合对随机噪声的不确定性分析提出了一种考虑噪声不确定性的工况传递路径改进方法。将SVR-OTPA方法应用于某型号双钢轮振动压路机驾驶室的噪声分析。采集实验工况数据建立OTPA模型，对压路机低频率、高振幅起振工况时的驾驶室司机耳旁噪声的空气声和结构声主要传递路径进行分析，为提出驾驶室司机耳旁噪声的降低方案提供依据。

1 考虑噪声不确定性的改进OTPA方法

1.1 OTPA方法的基本原理

OTPA方法是基于“传递率”概念的传递路径分析方法。传递函数是反映“激励-响应”之间的关系，而传递率则是反映“响应-响应”之间的关系。如图 1所示，测量激励源附近位置的响应(afi,pfi)，其与目标点之间的传递率可以分别表示为

(1)

式中：NTFi和NTFfi分别为激励源i和响应fi至目标点的噪声传递函数，Fi和Qj为激励处的力和声源强度，a和p分别为对应的加速度和声压。具体可参照图 1。

图1 OTPA模型Fig.1 OTPA model

设系统中共有n条传递路径，其中通过激励附近加速度响应建立的传递路径数目为r，则目标点的声压响应可以表示为

(2)

在工程实际中，通常将激励源邻域采集的工况数据整理为输入信号矩阵X，目标响应点在对应工况下采集的数据作为输出信号矩阵Y，输入-输出对应的传递率整理为传递率函数矩阵T，满足Y=X·T。则有

(3)

式中:GXX是输入信号的自功率谱矩阵，GXY是输入信号与输出信号间的互功率谱矩阵。定义X的伪逆X+=(XTX)-1XT。为使传递率函数矩阵T有解，GXX需要满足可逆条件，即要求工况数不小于输入信号的数目。

对于信号中噪声和串扰的部分，现有确定性方法如截断奇异值分解法[5](truncated singular value decomposition,TSVD)、Tikhonov正则化方法[10]和病态方程组求解法[8]均通过一定手段对其进行削弱。本文主要介绍具有代表性的TSVD方法。线性系统可以表示为

X·T=Ytrue+ε=Y

(4)

式中:ε为输入信号之间耦合串扰和噪声所引起的部分，是均值、方差均未知的微小量，Ytrue为系统输出的真实值。假设输入信号数目为n，工况数目为s，对输入信号矩阵X进行奇异值分解

X=UΣVT

(5)

式中:U为s×s的酉矩阵;V为n×n的酉矩阵；Σ为具有如下形式的s×n矩阵(s≥n)

(6)

其对角元素即为X的奇异值，并且满足σ1≥σ2≥…≥σn≥0。式(4)的解可以表示为

(7)

式中：ui，vi分别为U，V的列向量。由式(7)可以看出，越小的奇异值，就会将式中含有误差的第二项越放大，严重影响解的精度；如果奇异值等于零，则这一项将被无限放大，所取得的解则失去意义。因此，可以通过截断较小的奇异值来保证求逆运算的稳定性，根据奇异值大小占总信息量的百分比设定奇异值贡献率 (contribution rate,CR)为

(8)

(9)

式(9)表明后l项特征值满足CR≤τ，因此它们将被舍弃。如果l较小，则截断的项数较少，传递率函数矩阵估计值依然含有误差项，与未截断前可能相差并不大；而如果l较大，截断的数目较多，则有可能因为截取项过多而损失重要信息。

1.2 改进的OTPA方法

现有OTPA方法主要存在的不足包括：①分析结果准确性严重依赖于重要参数的选取，如截断奇异值方法中对阈值τ的取值；②方法没有考虑信号中因混有随机噪声而具有的不确定性。本文改进思路即从这两个方面入手，首先使用能够自适应工况数据调节参数的支持向量回归(support vector regression,SVR)方法对OTPA方法进行改进，然后在考虑噪声不确定性条件下进行分析。

1.2.1 支持向量回归改进的OTPA方法

对于如式(4)所示的线性系统，在噪声项没有足够先验知识的条件下，为使得模型在具有较好的拟合度的同时，又具有良好的泛化能力，可以使用支持向量回归方法。支持向量回归是一种通过对凸二次规划问题进行求解从而得到全局最优解的回归方法，因其回归性能良好而得到广泛应用。延续上节的基本设定，假设在每个频率点上有n个输入信号的s组工况数据，有数据对{(x1,y1),(x2,y2),…,(xs,ys)}⊂n×。理想状态下，希望通过数据拟合得到如下形式函数

f(x)=

(10)

考虑到信号中混有随机噪声等因素，不可避免会对中心值产生偏差。ε-SVR方法通过设定半径为ε的“不敏感管道”对拟合偏差绝对值超过ε的部分进行惩罚，偏差绝对值在ε内的则免于惩罚，也称作软边界损失。其示意图如图 2所示。

图2 软边界损失Fig.2 Soft margin loss

图2中阴影区域内的点在“不敏感管道”内，它们对损失函数没有贡献；阴影区域外的点则为离群点，它们是构成拟合函数的关键，因此称作“支持向量”。其对损失函数的贡献计算为

(11)

(12)

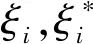
(13)

(14)

L(T,ξ,ξ*,α,α*,η,η*)取最优值时满足

(15)

将式(15)代入式(14)，原问题转化为求解如下优化问题

(16)

传递率函数矩阵可根据式(15)表示为

(17)

(18)

不敏感系数ε的作用是决定模型对于噪声的容许程度。ε取值过大，不敏感管道较宽，可能使模型回归误差增大；ε取值过小，不敏感管道较窄，支持向量的数目增多，同样会场产生过拟合而使模型的泛化能力下降。在实践中ε的取值应考虑训练样本的噪声程度，可以按如下公式求解

(19)

式中σ是对工况数据的噪声估计，按下式进行计算

(20)

(21)

1.2.2 噪声不确定性的量化方法

对于声学/振动信号的测量，其测试链一般包含如下过程：软件控制产生数字信号，由DAC转为模拟信号并经过功放将信号导入激振器；声振信号由激振器对被测装置激励而发出，由传感器接收并经过前置放大器进行放大，再经过ADC转为数字信号输入到软件中。噪声不确定性在测试链的多个环节均存在：ADC和DAC转换中由于对信号数据进行截尾或舍入产生量化噪声；信号通过功率放大器会产生共模噪声；在被测装置受到激振器激励而产生的声振信号一般具有空间指向性，其辐射场参数具有依频特性；此外，在存在多个被测装置时，其信号间的串扰耦合也会为系统引入不确定性。

OTPA方法需满足工况数不少于输入信号数目，即s≥n，考虑噪声不确定性的改进OTPA方法要求s′≥2n，这是为了保证在其后建模过程中包含每种关心的工况。现实中可能难以实现数量较多而互相不同的工况，因此可以在原s组工况之上，取相同的另外s组工况参与建模。由于随机噪声的存在，它们并不会完全相同。如果噪声程度很小，由于改进方法中不敏感管道的存在，新增的数据对回归结果不会产生较大影响；如果噪声程度较大，则新增数据与原数据存在较大差异，其分析结果具有较强的不确定性。在建模过程中采用“留一法”，即每次建模时留出一组数据，取s′-1组工况数据进行建模，在保证模型中包含了足够的有效信息的同时，使得随机噪声成为影响模型参数不同的唯一因素。在此方法下，能够获得s′组模型参数。预测结果的均值和方差对于分析由于随机噪声的混入而导致传递路径分析产生的不确定性具有重要的意义。一方面，均值能够直观反映主要传递路径，路径贡献均值较大的路径是所分析目标点响应的主要传递路径；另一方面，方差能够反映出该路径受随机噪声的影响程度，方差越大则噪声程度越大。如果某条传递路径贡献具有较大均值和较小方差，而另外一条传递路径具有较小均值和较大方差，在使用传统OTPA方法分析时，很可能出现后者的贡献值大于前者，从而导致错误的传递路径分析结果。

2 SVR-OTPA方法的有效性验证

2.1 数值仿真

为验证基于SVR-OTPA方法的路径贡献分析的有效性，根据“源-传递路径-接收者”模型，设计图 3所示的空间声场数值算例[12]。根据上节设定，取8个模拟实验工况和1个模拟测试工况。每个声源特征频率的工况安排如表 1所示。在数值模拟中各声源强度相同。声场中混有高斯噪声，其幅值为声源振动幅值的0.2倍。数值算例的求解方法可以参考已有文献[10,12]，本文不作详细展开。

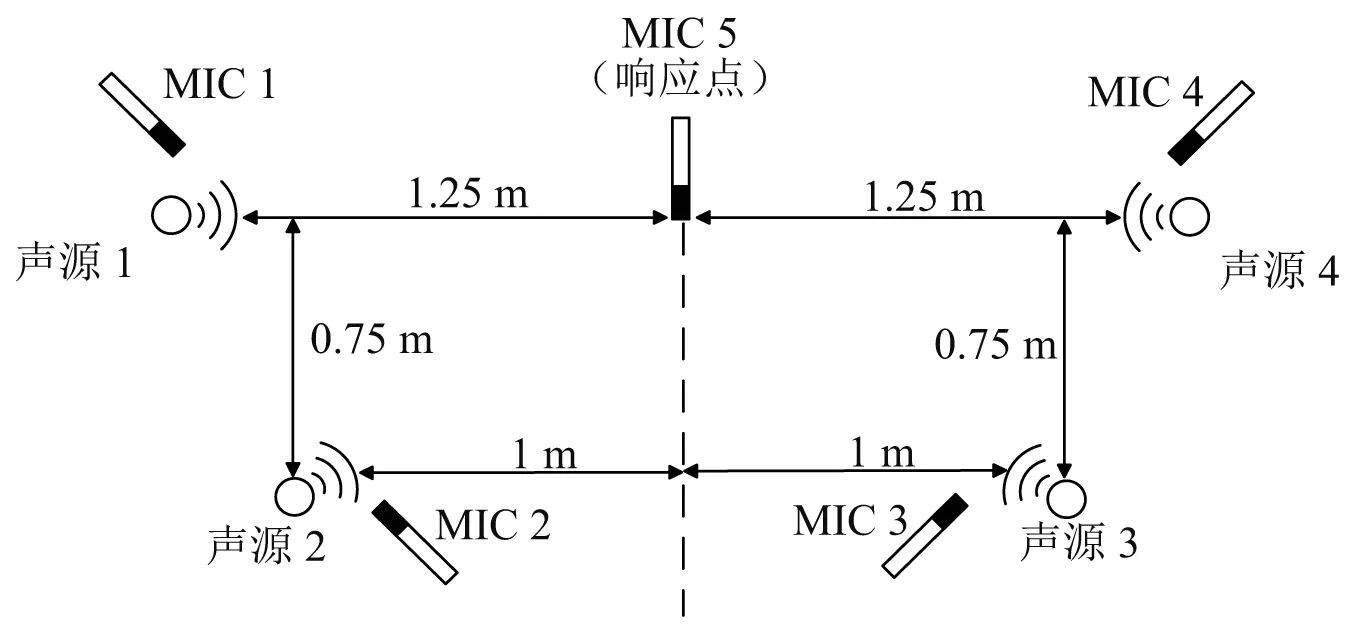
图3 数值算例的“源-传递路径-接收者”模型Fig.3 “Emitter-transfer path-receiver”acoustic model

表1 数值算例工况条件(特征频率)Tab.1 Operational conditions in numerical case (characteristic frequency)

根据前述传递率函数计算方法，分别使用截断奇异值分解法(“TSVD-OTPA”)、Tikhonov正则化方法(“Tikhonov-OTPA”)、病态方程组求解法(“病态方程-OTPA”)以及考虑不确定性的SVR改进OTPA方法(“SVR-OTPA”)建立相应的OTPA模型。利用这些模型分别对测试工况数据进行求解，并将求解得到的预测信号与实际仿真得到的信号进行对比，其结果如图 4所示。其中SVR-OTPA方法给出的预测信号结果，是由8组模拟工况应用“留一法”建立的7组模型得出结果的均值。图中结果表明，四种对传递率函数矩阵的处理方法所得到的预测信号均能够在较大程度上还原仿真结果信号，尤其是都能够捕捉到仿真信号中的特征频率(即20 Hz、30 Hz、40 Hz和50 Hz)。

图4 目标响应点信号：实线-仿真结果；虚线-SVR-OTPA；双点线-TSVD-OTPA；点划线-Tikhonov-OTPA；双点划线-病态方程-OTPAFig.4 Response point signal:solid line-simulation result;dashed line-SVR-OTPA;double dotted line-TSVD-OTPA;dash-dotted line-Tikhonov-OTPA;doubledot dashed line-Ill-posed function-OTPA

进一步地，分析每条传递路径对目标响应点的贡献，并对于4条传递路径在全频段计算四种OTPA方法的预测RMSE值如表 2所示。结果表明：就整体预测能力而言，SVR-OTPA方法和Tikhonov-OTPA方法性能相当，且优于TSVD-OTPA方法及病态方程-OTPA方法。而对于每条传递路径在特征频率上的贡献进行单独考察表明，就传递路径贡献量预测精确度而言，SVR-OTPA方法最高，Tikhonov-OTPA其次，而另外两种OTPA方法相对误差较大。

表2 数值算例中不同OTPA方法各路径贡献预测RMSETab.2 RMSE of path contributions using different OTPA methods in the numerical case

对四种OTPA方法在特征频率下路径贡献量预测值和每个声源单独仿真得到的路径贡献量真实值进行对比如图 5所示。比较仿真结果可以发现，TSVD-OTPA在特征频率50 Hz处预测值产生严重错误，影响了主导传递路径的判断。相比之，SVR-OTPA方法具有较高的整体预测精度，同时对于特征频率下的路径贡献也有较准确的预测值。Tikhonov-OTPA方法和病态方程-OTPA方法总体而言能够具备分析主要传递路径的功能，但在整体预测精度和特征频率下预测精度上略逊于不确定SVR-OTPA方法。

进一步地，由SVR-OTPA方法得到的路径贡献不确定性如图 6所示。图中展示了由SVR-OTPA模型对测试工况数据的预测均值及其95%预测区间(95 percent prediction uncertainty,95PPU)。图 6所示结果与特征频率下路径贡献度相比，路径1非特征频率噪声项的不确定性与路径2、3、4相比较大，而特征频率下噪声的不确定性可能将其贡献值抵消到与非特征频率路径贡献相当的水平，即噪声的不确定性对于路径1的影响较大。噪声的高不确定性给出了图 5中四种OTPA方法对路径1特征频率下贡献估计偏低的解释。同理，路径4尽管非特征频率下噪声的不确定性程度较小，但在特征频率下具有很高的不确定性。对路径2、3，其特征频率下噪声不确定性高于非特征频率段噪声的不确定性，但因其幅值较小，并不影响特征频率的识别。

图5 特征频率下各路径贡献Fig.5 Path contributions at characteristic frequency

图6 数值算例路径贡献不确定性Fig.6 Uncertainty of path contribution in numerical case

2.2 实验验证

为确认SVR-OTPA方法在实际应用中的有效性和精确度，根据上述数值仿真算例中的设定进行验证实验。实验环境为本底噪声为15.6 dB的半消声室。实验中使用活塞式扬声器代替数值算例中的点声源，使用ICP传声器采集声源附近参考点和目标响应点的声压数据。实验系统和实验现场照片分别如图 7和图 8所示。由于实验用小尺寸扬声器对于低频信号的表现力较差，数值算例中的特征频率不再适用。实验工况制定如表 3所示。

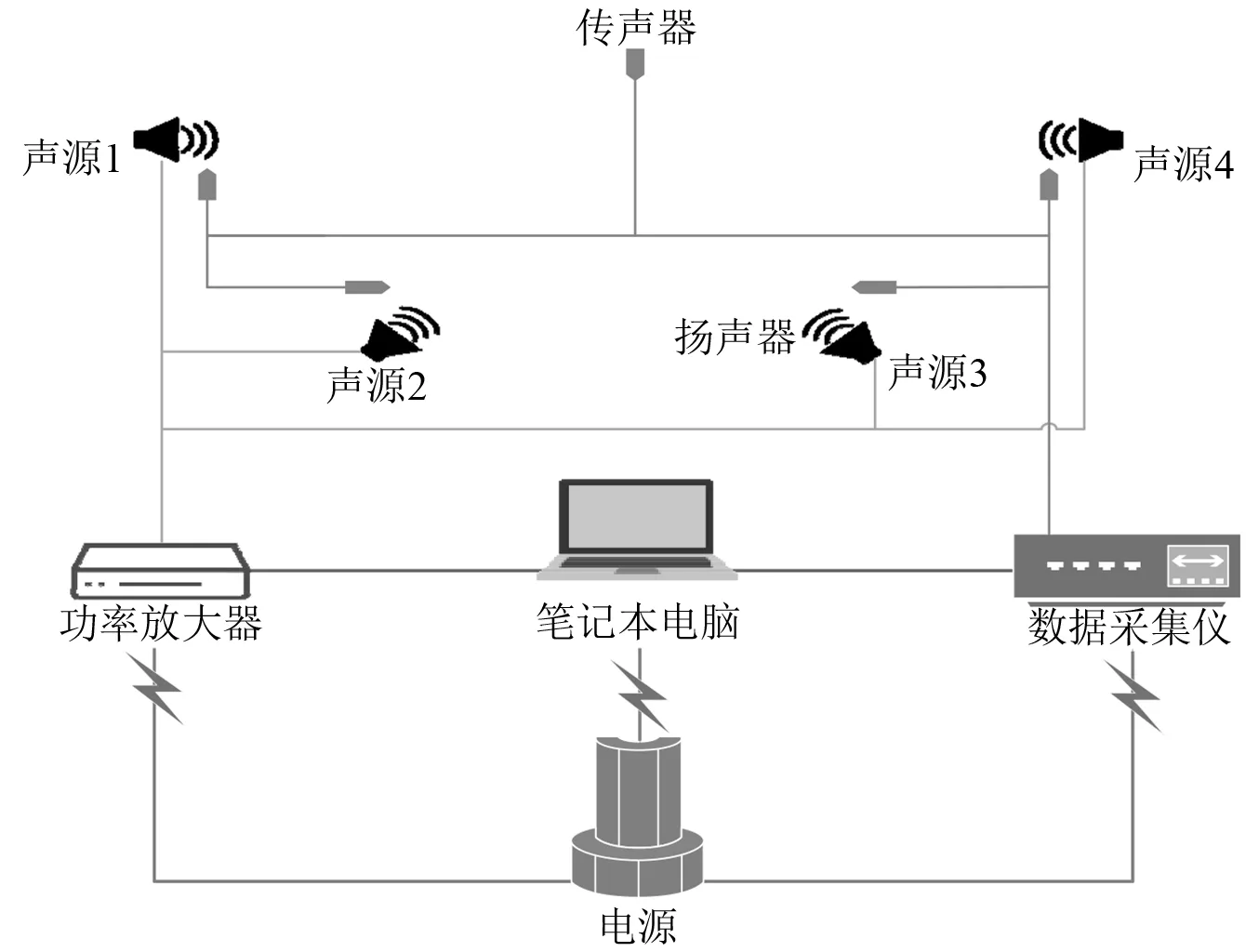
图7 实验系统Fig.7 Experiment system

图8 实验现场Fig.8 Experiment layout

表3 实验工况条件(特征频率)Tab.3 Experimental operational conditions (characteristic frequency)

对四种OTPA方法得到的路径贡献量预测值和实验中测量得到的路径贡献量真实值进行对比如图 9所示，各个方法的RMSE值如表 4所示。可见，SVR-OTPA方法和TSVD-OTPA方法在整体预测精度和路径预测精度上都要优于另外两种方法。TSVD-OTPA方法在多条传递路径上的预测精度略优于SVR-OTPA方法。然而，如图 9(4)所示，在特征频率988 Hz处，由于噪声不确定性，TSVD-OTPA和Tikhonov-OTPA方法的预测值都产生了较大偏差。其中TSVD-OTPA方法预测值偏差尤为严重，甚至有可能影响该特征频率下主导传递路径的辨识结果。

图9 特征频率下各路径贡献Fig.9 Path contributions at characteristic frequency

表4 实验中不同OTPA方法各路径贡献预测RMSETab.4 RMSE of path contributions using different OTPA methods in the experimental case

综合上述分析结果，可见TSVD-OTPA虽然在整体路径贡献量预测上具有较高精度，但在某些特征频率处预测值产生严重错误，影响了主导传递路径的判断。这与数值仿真得到的结果相一致，即在人为设定的截断阈值下，TSVD-OTPA方法有时会因截断过多有效信息而产生错误的预测结果。相比之下，不确定SVR-OTPA方法具有较高的整体预测精度，同时对于特征频率下的路径贡献也有较准确的预测值。而Tikhonov-OTPA方法和病态方程-OTPA方法总体而言能够具备分析主要传递路径的功能，但在整体预测精度和特征频率下预测精度上逊于不确定SVR-OTPA方法。因此，SVR-OTPA方法具有较高的整体预测精度，同时对于特征频率下的路径贡献也有较准确的预测值。

3 SVR-OTPA在压路机驾驶室司机耳旁噪声分析中的应用

3.1 OTPA“源-路径-接受体”信号测试

压路机驾驶室耳旁噪声主要来源于空气声传递和结构声传递两部分，本文以这两种噪声传递路径为研究对象。经过前期测试，可以确定该双钢轮振动压路机对外通过空气声辐射噪声的主要噪声源，即发动机所在的动力舱两侧、前、后钢轮的左、右两侧以及排气孔附近。而对于结构声的传播，则结合空气声测试结果及过往振动测试经验，取发动机和钢轮这两个主要振源与车架的连接处作为振源。在确定激励源基础之上，在每个激励源邻域布置参考点测点，采集作为OTPA模型的输入信号，部分测点布置的照片如图 10所示。

图10 信号测试点Fig.10 The experimental testing points

采集的输入信号中噪声信号共有7个通道，加速度信号共有18个通道(每个加速度传感器采集三个方向的振动加速度信号)。对于空气声传递路径，定义Path 1～Path 7分别为噪声信号测点到达司机耳旁目标响应点的传递路径；对于结构声传递路径，Path 1～Path 18的名称定义如表 5所示。

表5 结构声传递路径Tab.5 Structure-borne sound transfer path

压路机工作时主要存在三种工况：①发动机额定转速，钢轮不起振；②钢轮低频率、高振幅振动；③钢轮高频率、低振幅振动。本文相关分析主要在第2种工况下开展，即钢轮呈低频率、高振幅振动状态，其振动的特征频率为53 Hz。

3.2 司机耳旁噪声的SVR-OTPA模型建立

3.2.1 主要传递路径的遗漏检验

目标响应点的频率响应曲线如图 11所示。图中显示频域响应曲线出现了明显的特征频率53 Hz时域响应呈现周期性变化的原因即是前、后钢轮的振动频率由于控制误差而产生微小差距，使得前、后钢轮对外辐射噪声叠加呈现拍振现象。进一步观察发现其在特征频率下的幅值远高于其他非特征频率，因此可以得出此工况下噪声能量主要集中于低频 (0～500 Hz)。

图11 目标响应点测试频响应(上图-时域响应；下图-频域响应)Fig.11 Time &frequency domain response of target response point at testing operational condition 2;fig above-time domain response;fig below-frequency domain response

使用重相干函数法对双钢轮振动压路机驾驶室司机耳旁噪声是否遗漏主要传递路径进行检验。分别另外选取(不参与构建输入信号的)两组平稳运行状态下，压路机在钢轮低频率、高振幅振动的测试工况的数据作为测试分析数据。分别考察其目标响应点频谱曲线以及和各参考点信号的重相干函数值。

对该测试工况的各参考点信号与目标响应点信号的重相干函数进行计算，得到如图 12所示结果。可见在1 000 Hz以下，重相干函数值基本大于0.8，说明没有重要的传递路径遗漏，可以使用设定的输入信号构建SVR-OTPA模型。

图12 参考点信号与目标响应点信号的重相干函数Fig.12 Multiple coherence function

3.2.2 SVR-OTPA模型建立与预测结果

根据SVR-OTPA方法原理，利用构建的输入信号矩阵和对应的目标响应点矩阵建立模型。使用模型处理测试工况的数据，得到预测结果与测试实际信号对比如图 13所示。

图13 预测信号与测试信号Fig.13 Predicted signal &testing signal

可见，预测信号与测试信号在分析频段上具有相同的量级和变化趋势，在特征频率(53 Hz)及其他峰值频率上与测试信号具有很高的吻合度。在少数频段(如350～400 Hz)预测信号与测试信号有所偏差，实际信号在此频段内某些频率点上的声压响应很小，对于总体响应的贡献较少，因此这种偏差是可以接受的。

利用SVR-OTPA方法对该型双钢轮振动压路机驾驶室司机耳旁噪声的主要传递路径进行分析，分别对空气声传递路径和结构声传递路径贡献量进行识别和对比，从而确定两种不同传播方式的主要传递路径。

3.3 司机耳旁噪声的路径贡献分析

3.3.1 空气声主要传递路径分析

测试工况下特征频率下空气声各传递路径贡献如图 14所示。图中显示路径3和路径4是主要的传递路径。其中路径4贡献量约为30，路径3贡献量约为15，路径1和路径2贡献量均小于10。相比之下，路径5～路径7贡献量较小，而路径7的贡献量略大于路径5和路径6。总结而言，该测试工况下司机耳旁目标响应点的主要空气声传递路径为前、后钢轮两侧辐射噪声向驾驶室的透射，特别是通过隔声量较低的门窗密封件，其中后钢轮两侧辐射噪声是最主要噪声贡献源。而发动机噪声和排气孔噪声所在的传递路径对司机耳旁噪声贡献相对较小。

图14 特征频率下空气声各路径贡献Fig.14 Airborne sound transfer path contribution at characteristic frequency

进一步考察四条主要传递路径在分析频段上的不确定性，结果如图 15所示。图中黑色实线代表SVR-OTPA模型的输出均值，灰色区域代表输出结果的95%预测区间。由图中结果可以看出，空气声四条主要传递路径能量集中在特征频率53 Hz，在200 Hz以下具有较明显的不确定性。在该特征频率，路径1最高贡献量可达10.4，路径2最高贡献量可达12.8，路径3最高贡献量可达20.6，而路径4最低贡献量可达25，说明主要空气声传递路径不会因不确定性而产生误判。

图15 空气声传递路径贡献及其不确定性Fig.15 Uncertain path contribution of airborne sound

考察分析如图 16所示的频段上各传递路径贡献的分布，主要声压贡献频率集中在250 Hz以下，路径1～路径4以及路径7在此频段内有较高贡献量，而路径5和路径6则只在某些频率点上具有相对较高的贡献量。

图16 空气声传递路径贡献分布Fig.16 Airborne sound transfer path contribution distribution

3.3.2 结构声主要传递路径分析

特征频率点的结构声各传递路径贡献辨识结果如图 17所示。图中显示结构声路径5和路径6对司机耳旁目标响应点的声压贡献较大，属于主要传递路径。其中路径5声压贡献量最大约为50，路径6声压贡献量最大约为40，其他传递路径声压贡献量则均低于20，路径7～路径18声压贡献量很小甚至几乎无贡献。这些结果表明，测试工况下司机耳旁目标响应点的主要结构声传递路径为压路机前钢轮右侧Y方向和Z方向的振动，后钢轮和发动机的振动均不构成司机耳旁目标响应点声压的主要贡献源。

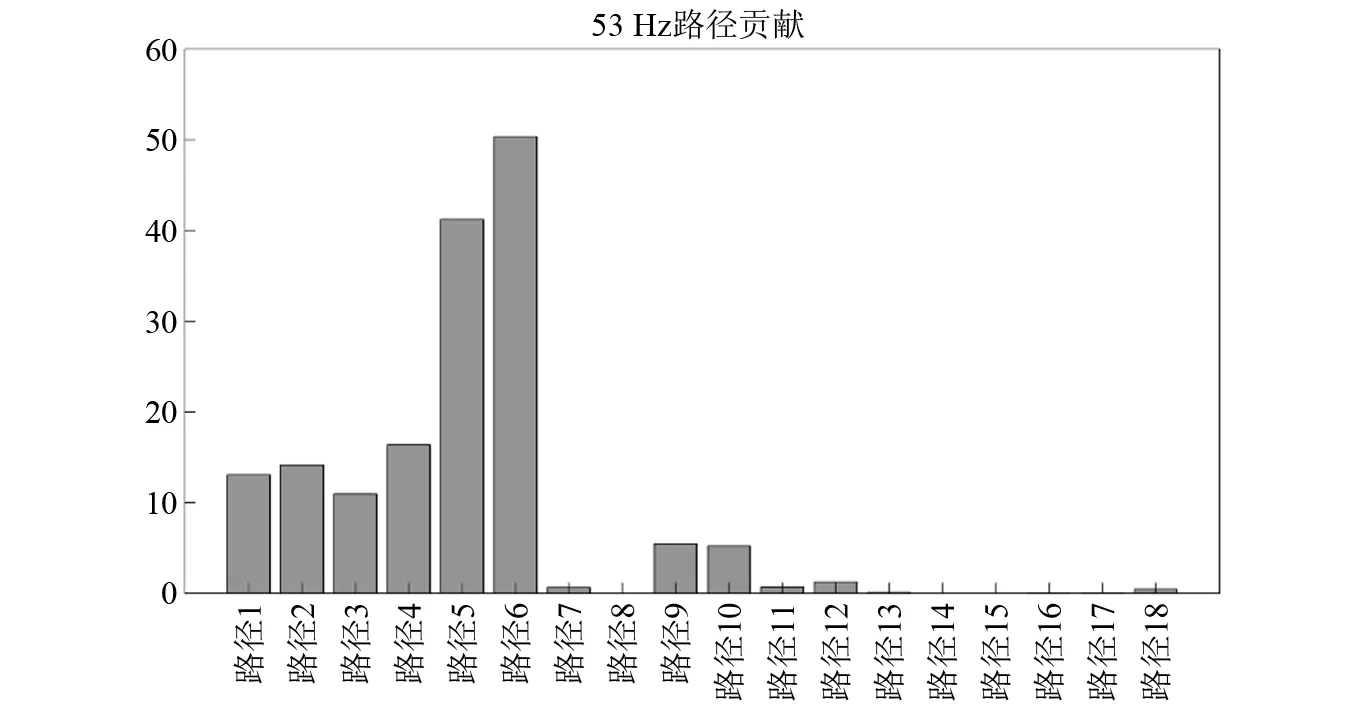
图17 特征频率点的结构声各路径贡献Fig.17 Structure-borne transfer path contribution at characteristic frequency

分析频段上各传递路径贡献的分布如图 18所示。路径5与路径6两条主要传递路径声压贡献集中在低频，非主要传递路径如路径11～路径14在全频段上均存在声压贡献。路径4、路径8和路径17在高频段上几乎无贡献。

图18 结构声传递路径贡献分布Fig.18 Structure-borne sound transfer path contribution distribution

3.4 分析结果

根据上节对振动压路机驾驶室空气声、结构声传递路径的分析，可以得到如下两点分析结果：

(1)司机耳旁目标响应点的主要空气声传递路径为前、后钢轮两侧的辐射噪声通过隔声量较小的门窗密封件向驾驶室内的透射，其中后钢轮两侧漏声是最主要噪声贡献源；

(2)主要结构声传递路径为压路机前钢轮右侧Y方向和Z方向的振动传到驾驶室结构振动从而引起司机耳旁噪声，后钢轮和发动机的振动所在的传递路径对司机耳旁噪声的贡献相对较小。

4 结 论

本文提出了一种在考虑噪声不确定性情况下，结合支持向量回归理论的改进工况传递路径分析(SVR-OPTA)方法。与现有方法相比，本文提出的改进方法具有高准确度、高可靠性的特点。通过“声源-传递路径-接收者”模型设计了空间声场数值算例，并结合验证实验验证了SVR-OTPA方法即使在输入信号混有随机噪声和串扰的情况下，依然能够准确预测路径贡献并成功辨识主要传递路径。在工程实践中，将SVR-OTPA方法应用于某振动压路机驾驶室噪声分析，成功辨识出驾驶室司机耳旁噪声的主要空气声和结构声传递路径。