基于动载试验荷载效率的简支梁桥冲击系数研究

周勇军，赵 洋，赵 煜，曹 群，李 珍

(1.长安大学 公路学院，西安 710064；2.长安大学 公路大型结构安全教育部工程研究中心，西安 710064；3.呼和浩特市市政工程管理局，呼和浩特 010020)

冲击系数是车辆激励下，桥梁产生的结构动力效应与相应竖向静力效应的比值。引入冲击系数的概念可以有效地将桥梁结构复杂的动力问题静力化，是研究车桥的耦合作用以及检测现役桥梁动力性能的重要内容之一。但冲击系数有很大的随机性[1]，且受到众多因素的影响[2]，因此众多学者对冲击系数进行了大量的研究与评价。桥面平整度是影响冲击系数的重要因素，众多研究表明冲击系数随着桥面平整度状况变差而减小[3-5]。

车辆模型的不断完善使的车桥耦合振动的更加贴近实际，Wang等[6]提出三轴车辆模型；Obrien等[7]参考欧洲大量卡车统计数据采用五轴车模型；蒋培文等[8]提出了四自由度双轴平面车辆模型、五自由度三轴平面车辆模型、九自由度三轴空间车辆模型等车辆模型；邓露等[9]基于中国桥梁规范中的设计车辆荷载，提出了一组5轴车辆模型参数；吴铭汉等[10]对比了移动弹簧-质量、四分之一、二分之一及整车模型的冲击作用，结果显示，二分之一车辆模型和整车模型作用下冲击系数计算良好。

对车辆数和车辆加载位置对冲击系数影响的研究方面，Huang等[11]发现车辆不同加载位置使混凝土梁桥各主梁上的冲击系数发生变化；单辆车的静荷载效应较小，但冲击系数不一定小，甚至大于规范值[12-13]；研究表明单辆车的冲击系数比多辆车冲击系数大[14-15]。

在车重作用分析方面，研究表明冲击系数随着车重增加而减小[16]，也有研究认为冲击系数随着静力效应增大而减小[17]，二者规律一致，韩万水等[18]计算特重车荷载下的冲击系数，指出特重车荷载下的冲击系数小于现行规范值。

我国现行规范JTG D60—2015《公路桥涵设计通用规范》中规定冲击系数的取值仅与桥梁结构基频有关，计算公式是对6座钢筋混凝土桥及1座预应力钢筋混凝土通过现场实测的数据统计回归分析得到，样本数较少且种类单一，部分学者也对其适应性进行质疑[19]，现行规范采用均布力加集中力作为桥梁设计荷载形式，无法直接展现移动车辆荷载对桥梁结构的冲击作用。若要研究设计荷载作用下的冲击系数，应采用与规范规定的设计荷载标准值相近的车辆荷载或等效的随机状态进行研究，而现行规范中规定的车道荷载为均布力和一个集中力，均布力加集中力的车桥耦合振动可以近似的通过数值模拟来实现，但在实测中对于均布力加集中力用车辆荷载无法实现。因此采用现行规范中规定的车道荷载进行冲击系数分析没有实际工程价值。

冲击系数是汽车荷载标准值的放大系数，而不是单一或少数车辆荷载的冲击作用[20]。上述研究表明，车辆载重较小时，相比重车会产生较大的冲击系数，而静载时效应较小，虽然得到冲击系数较大，但总的荷载效应仍然较小，这样获取的冲击系数没有实际意义。但在实际桥梁动载试验中通常仅采用一辆车或两辆车进行试验，此时并不是在设计荷载下的标准试验，缺乏与规范设计值的对比依据。

基于此，本文以标准跨径简支小箱梁桥为研究对象，采用桥梁动载试验常见的三轴重车来等效还原设计车道荷载，考虑跨径、桥面平整度、速度等因素的影响，进行准设计状态车桥耦合振动分析，以此研究等效设计荷载作用下的冲击系数，并与规范值进行对比；其次研究动载试验荷载效率与冲击系数的关系，分析不同因素对冲击系数的影响规律；最后提出基于动载试验荷载效率的轻荷载冲击系数修正方法，建立轻荷载试验冲击系数与准设计状态冲击系数之间的关系，为桥梁动载试验实测冲击系数值的评价提供依据。

1 车桥耦合冲击系数分析理论

1.1 冲击系数计算方法

公路桥梁设计规范中一般采用动力冲击系数来表征车辆对桥梁结构产生的动力冲击效应。冲击系数是汽车过桥时对桥梁结构产生的竖向动力效应的增大系数。车辆荷载的冲击系数可表示为：

(1)

式中：Yjmax为在车辆过桥时测得的效应时间历程曲线上最大静力效应处量取的最大静力效应值；Ydmax为在效应时间历程曲线上最大静力效应处量取的最大动效应值。

本文采用的最大动力效应由车辆过桥时的挠度时程曲线获得，最大静力效应为车辆低速过桥(准静态)时结构的最大动力效应值。

1.2 车辆模型及振动方程

参考JTG/T J21-01—2015《公路桥梁载荷试验规程》[21]，本文选择桥梁动载试验的主流车型三轴载重车为试验加载车，采用五自由度三轴平面车辆模型，并选用了尽可能还原荷载试验中实际三轴载重车的模型参数，车辆模型如图1所示，模型参数见表1[22]。美国AASHTO桥梁规范中的主要设计车辆HS20-44三轴卡车模型规定悬架力是由线性弹簧的弹性弹簧力组成的，轮胎弹簧和所有阻尼器均可被认为是线弹性的，众多学者[6,16-17]在研究车重多冲击系数影响时，均采用的线弹性弹簧力为悬挂力，认为车重在合理取值范围内，悬挂弹簧、轮胎弹簧及阻尼器均可被认为是线弹性的，即车体重量在合理范围内调整时，悬挂参数是不改变的。相关标准DB61/T 916—2014《公路桥梁(梁式桥)荷载试验技术规程》[23]规定，三轴载重车总重不宜大于38 t，且单轴重不大于16 t，参照相关规范并结合所选车型，本文选择载重在25～38 t的车辆进行分析，通过改变表1中车体质量参数来实现调整车辆载重，悬挂参数不变。

表1 车辆模型参数Tab.1 Vehicle model parameters

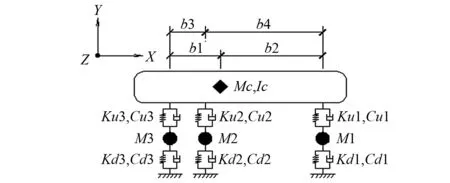
图1 五自由度三轴平面车辆模型Fig.1 Five-degree-of-freedom three-axis planar vehicle model

图1中，车体质量Mc有仰俯旋转自由度α和竖向位移z，构架与轮对质量之和M1、M2、M3的竖向位移自由度z1、z2、z3，Ku、Cu为一系悬挂刚度、阻尼，Kd、Cd为二系悬挂刚度、阻尼。

根据达朗贝尔原理可得三轴平面车型振动方程：

(2)

式中：[Mv]、[Cv]、[Kv]分别为质量矩阵、阻尼矩阵、刚度矩阵；{Fbv}为轮胎与桥面接触点处的瞬时耦合荷载向量；{Gv}为重力荷载向量。

1.3 桥梁模型

本文以标准跨径的简支小箱梁桥为研究对象，计算跨径分为20 m、30 m、40 m，桥面净宽11 m，横向布置4片梁，20 m跨径小箱梁横断面形式如图2所示，运用ANSYS有限元程序建立空间梁格模型，如图3所示。

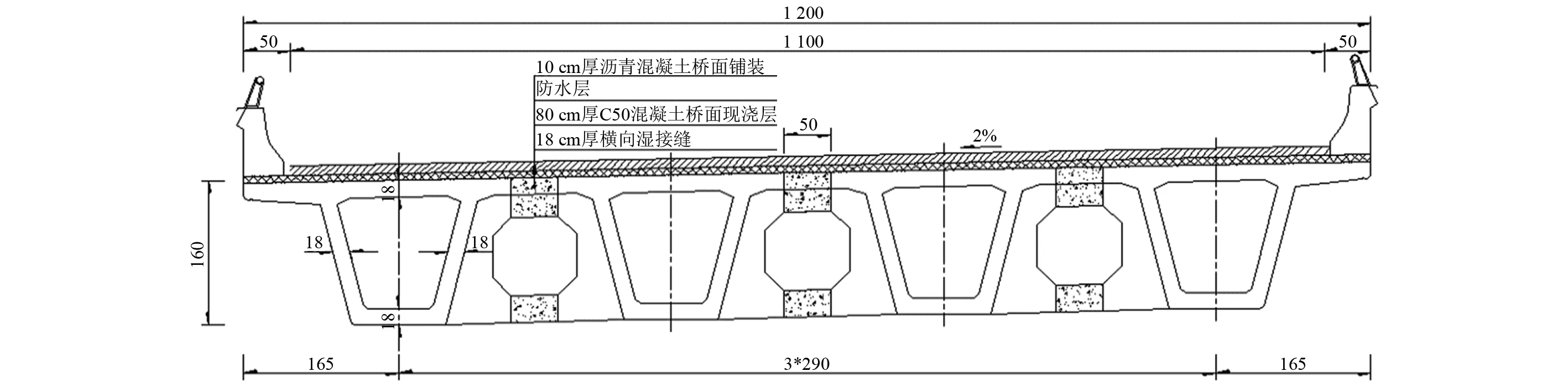
图2 简支小箱梁桥横断面图(cm)Fig.2 Cross section of simply supported box girder bridge(cm)

图3 简支小箱梁桥模型示意图Fig.3 Model diagram of simply supported box girder bridge

1.4 桥面平整度

桥面平整度是影响车桥耦合振动的重要因素，本文采用傅里叶变逆换法并参考GB7031—1986《车辆振动-路面平度表示方法》生成桥面平整度样本。

傅里叶逆变换的平整度数值模拟计算模型如下式：

(3)

式中：xm为平整度的离散序列,Xk为离散傅里叶变换信号的模值；N为采样点数。

由调查可知，我国桥面平整度大多处于A、B、C三个等级范围内，因此以A、B、C三个等级的平整度作为研究参数，一组桥面平整度曲线如图4所示。为减小不同桥面平整度样本对计算结果的影响，使本文计算结果具有较好的代表性，每一个工况选取10组桥面平整度样本计算动力响应，求10组样本动力响应的平均值作为该工况计算结果。

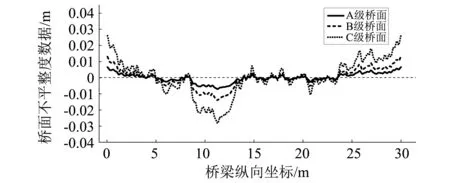
图4 一组桥面平整度曲线Fig.4 A set of bridge deck flatness curves

2 准设计状态下冲击系数的分析

要正确评价冲击系数，首先要采用与设计荷载等效的车辆荷载，进行准设计状态下的冲击系数研究。

2.1 分析方法及实例验证

本文采用ANSYS的二次开发语言APDL对车桥耦合振动进行数值分析[24]，借助APDL语言实现车辆移动过程中对式(1)中{Fbv}的瞬时计算，将式(1)中{Gv}+{Fbv}荷载施加于各节点，并调用ANSYS的时程分析功能对每个子步计算，解出车桥之间的接触力，进而计算时程响应。

为验证本文程序的正确性，采用经典文献[25]中的桥梁与车辆参数，将文献中计算结果与本文程序计算结果进行对比，文献中计算结果如图5(a)所示，本文程序的计算结果如图5(b)所示。对比分析可知，本文程序计算结果无论是数值大小还是变化趋势均与参考文献吻合。通过将本程序有限元计算值与实测值进行对比发现吻合度较好，验证了车桥分析方法及本文数值计算结果的准确性。

图5 不同速度移动荷载作用下桥梁跨中的位移响应Fig.5 Displacement response of bridge midspan under moving loads at different speed

2.2 准设计状态的概念

荷载效应等效比计算式：

(4)

式中：η为荷载效应等效比；Ss为静载作用下，某一加载试验项目对应的加载控制截面内力或位移的最大计算效应值；S为控制荷载作用下控制截面内力或位移的最不利效应计算值(不计冲击效应)；控制荷载为进行荷载试验所确定的荷载，可用来确定荷载试验效率，这里指设计荷载。

2.3 准设计状态的车辆布载

由简支小箱梁桥横断面的对称性，选择1#、2#主梁分析。车辆布载参照规范，横向车间距为1.3 m，纵向车间距为5 m，纵向车辆首尾衔接。将车辆重量分配在车辆各轴，通过将车辆各轴在简支梁各片梁跨中位置处的纵向位移影响线上加载，得到在简支梁跨中位置产生最大位移效应时的各轴的纵向位置，从而确定准设计状态车辆加载位置，车辆布载方式如图6所示。

计算各跨径简支小箱梁桥在公路Ⅰ级设计汽车荷载(不计冲击系数)作用下跨中控制截面的挠度效应值，然后将车辆按照图6的布载方式加载，调整车辆载重，并按式(4)计算各跨径桥梁跨中1#、2#主梁挠度效应等效比，使其等于或接近1，达到准设计状态。计算结果见表2。

图6 车辆布载方式(cm)Fig.6 Vehicle loading mode(cm)

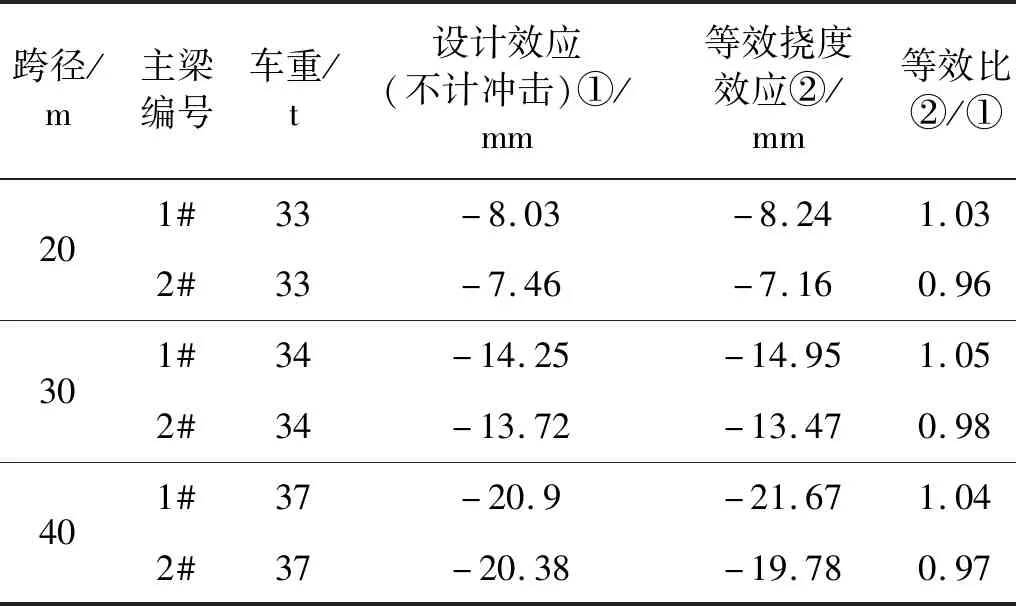
表2 简支小箱梁桥跨中挠度效应等效计算结果Tab.2 Equivalent calculation results of mid span bending moment effect of simply supported box girder bridge

参考JTG/TJ21-01—2015《公路桥梁荷载试验规程》[21]，当荷载效应等效比介于0.95～1.05之间，则认为车辆荷载效应与设计荷载效应等效，此时称为准设计状态。

2.4 准设计状态冲击系数分析

结合我国桥面实际情况，选取三个行驶速度20 km/h、60 km/h、100 km/h表征低、中、高速行驶状态，考虑A、B、C三个桥面平整度等级，同时选取十组桥面平整度样本对20 m、30 m、40 m跨径简支小箱梁桥进行准设计状态下车桥耦合振动分析，取10组样本动力响应的平均值作为计算结果，车辆横断面布载形式见图6。

任一跨径桥梁的分析工况排列组合共计18个，对各工况的车桥耦合振动问题进行求解，得到挠度时程曲线，部分40 m跨径小箱梁在B级桥面平整度下的挠度时程曲线见图7。

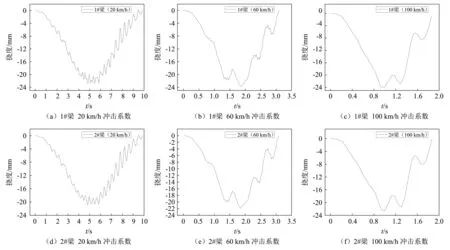
图7 40 m跨径小箱梁挠度时程曲线Fig.7 Deflection time-history curve of 40 m span box girder

为了直观分析简支小箱梁桥各主梁在准设计状态下的冲击系数，定义冲击系数计算值超过规范值的工况数与总的工况数的比值为超规范工况百分比，按照15规范计算冲击系数的规范值，将简支小箱梁桥所有工况的冲击系数计算结果进行统计分析后，汇总于表3。

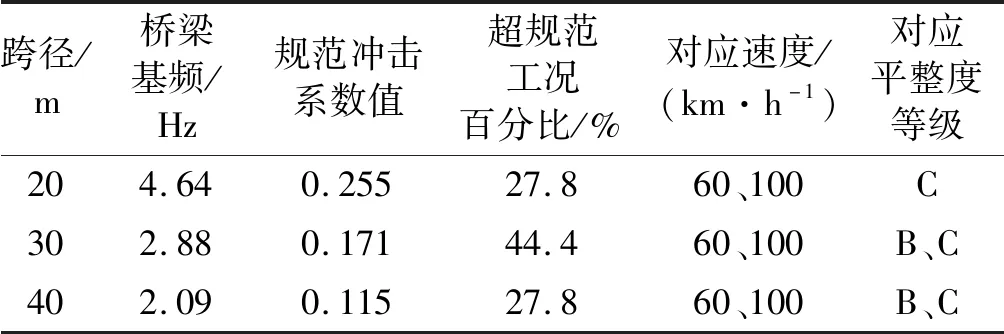
表3 简支小箱梁桥挠度冲击系数超工况统计Tab.3 Working condition statistics of deflection impact coefficient of simply supported box girder bridge

由表3可得，桥梁跨径为30 m时超规范工况百分比最大。分析其原因，通过ANSYS有限元程序建立了如图1所示的车辆系统模型，调整车辆载重，进行模态分析，采用LANB法提取相应的车辆竖向自振基频，30 m跨径桥梁对应加载车的车辆系统的竖向自振基频为2.77 Hz，30 m跨径小箱梁的基频为2.88 Hz，30 m跨径小箱梁的基频与车辆悬挂系统的竖向自振基频较为接近，使系统振幅增大，造成30 m跨径小箱梁的冲击系数超规范工况百分比最大。

速度对冲击系数的影响规律不明显，各跨径小箱梁超规范工况均出现在中、高速。超规范的工况均发生在B、C级平整度桥面，可见桥面平整度对冲击系数影响非常大。对于各跨径简支小箱梁桥，按规范取值的冲击系数与偏不安全，但在桥面状况良好和低速行驶时安全性较高。

3 动载试验荷载效率下冲击系数分析

通过调研大量动载试验工程实例，发现在相关规范[21,23]对加载效率无明确规定的前提下，为测试简便与保证试验安全，实际简支梁桥动载试验时，通常仅采用单辆25～38 t的三轴载重车进行加载，此时动载试验荷载效率较小。

通过改变车辆的载重为25～38 t来模拟动载试验荷载效率的变化，选择20 km/h、60 km/h、100 km/h表征低、中、高速行驶，考虑A、B、C三个桥面平整度等级，并取10组平整度样本计算20 m、30 m、40 m跨径简支小箱梁桥在不同动载试验荷载效率下的冲击系数，来分析动载试验荷载效率对桥梁冲击系数的影响，并对轻荷载作用下的冲击系数进行修正分析。

3.1 动载试验荷载效率计算

(1)动载试验荷载效率计算式：

(5)

式中：ηd为动载试验荷载效率；Sd为动载试验荷载作用下控制截面的最大内力或变形；S为控制荷载作用下控制截面的最大内力或变形(不计冲击)；控制荷载为进行荷载试验所确定的荷载，可用来确定荷载试验效率，这里指设计荷载。

(2)车辆荷载作用方式

为使研究模拟过程贴切实际，车辆行驶车道宽度取值3.5 m，且车辆始终行驶在车道中间。以1#梁作为研究对象，由于车道宽度3.5 m，轮距为1.8 m，车辆横向布置在距护栏0.85 m处；以2#梁作为研究对象，车辆横向布置在2#梁的中心线处，具体布载方式如图8所示。

图8 简支小箱梁桥单辆车横向布载示意图(cm)Fig.8 Schematic diagram of lateral load of single vehicle on simply supported box girder bridge(cm)

(3)动载试验荷载效率计算

按图8的布载方式将单辆车荷载加载在桥梁跨中位置纵向位移影响线的最不利位置处，并通过改变三轴车辆的载重为25 t、30 t、35 t、38 t，来模拟动载试验荷载效率的改变。按式(5)计算各跨径简支小箱梁桥1#、2#主梁的跨中挠度效应的动载试验荷载效率，计算结果见表4所示。

表4 简支小箱梁桥跨中挠度效应动载试验荷载效率Tab.4 Effect of deflection in midspan of simply supported box girder bridge load efficiency of dynamic load test

3.2 动载试验荷载效率对冲击系数的影响

对20 m、30 m、40 m跨径简支小箱梁桥进行车桥耦合振动分析，三轴车辆载重以25 t、30 t、35 t、38 t变化来模拟动载试验荷载效率的改变。考虑A、B、C三个桥面平整度等级，并选择10组平整度样本，同时选取三个行驶速度20 km/h、60 km/h、100 km/h表征低、中、高速行驶。

对各工况进行车桥耦合振动求解，得到简支小箱梁桥的挠度时程曲线，根据时程曲线计算冲击系数，将1#、2#梁的挠度冲击系数按不同速度绘制于图9～图11，分析冲击系数随动载试验荷载效率改变而变化的规律。

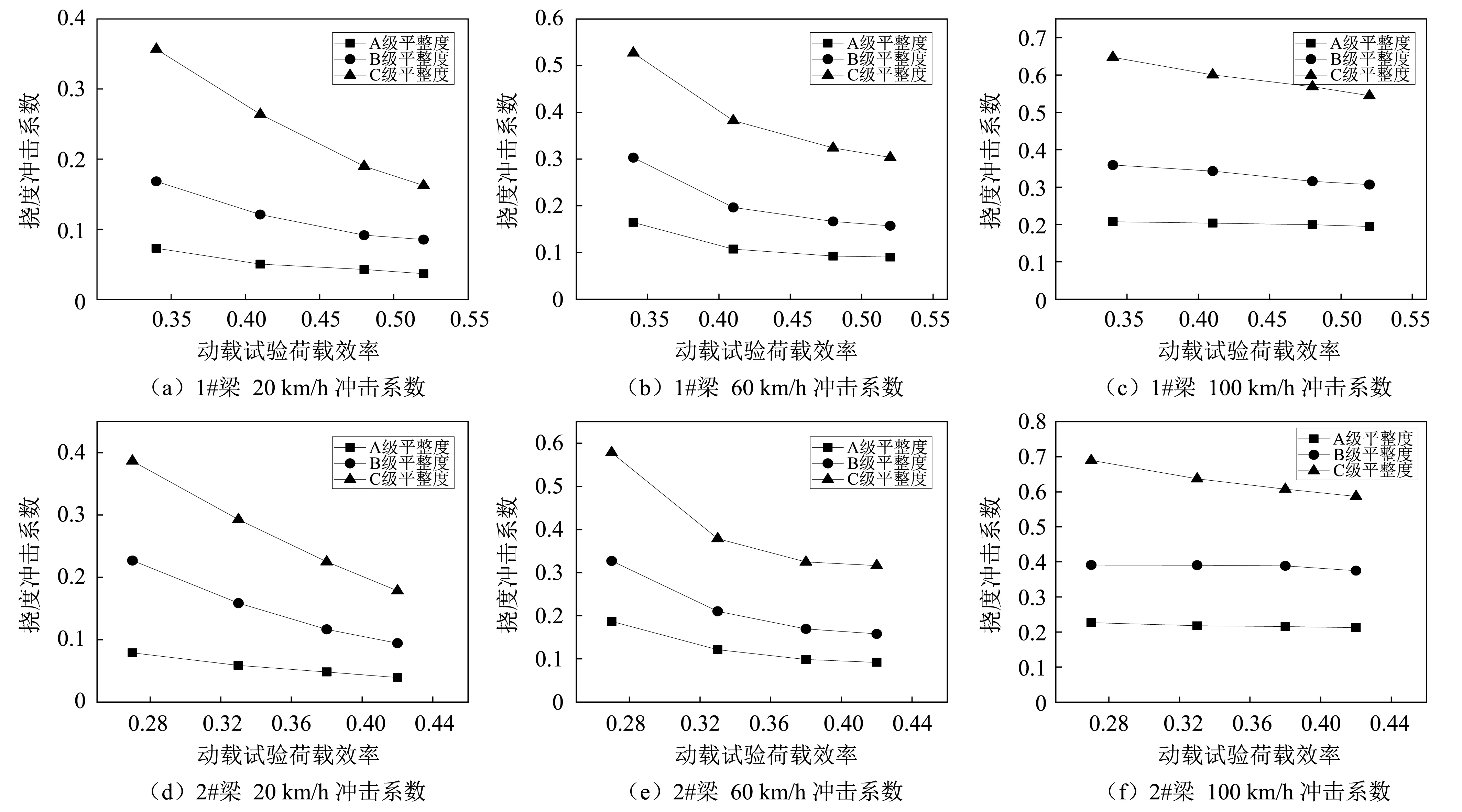
图9 20 m跨径简支小箱梁挠度冲击系数Fig.9 Deflection impact factor of 20 m span simply supported box girder

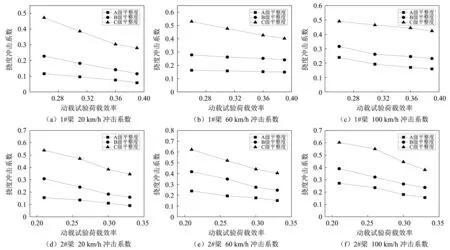
图10 30 m跨径简支小箱梁挠度冲击系数Fig.10 Deflection impact factor of 30 m span simply supported box girder

图11 40 m跨径简支小箱梁桥冲击系数Fig.11 Deflection impact factor of 40 m span simply supported box girder

由图9～图11分析可得，在单辆车荷载作用下，基于动载试验荷载效率，各跨径简支小箱梁1#、2#的挠度冲击系数有如下特征：

(1)总体来讲，1#、2#梁的挠度冲击系数随着动载试验荷载效率的增大而逐渐减小，且递减速率逐渐变小，说明轻荷载容易产生更大的冲击系数。

(2)随着桥面平整度状况变差，各片梁挠度冲击系数随动载试验荷载效率变化的趋势变陡，随着动载试验荷载效率的增大，各平整度下的趋势线间的距离减小，当动载试验荷载效率最小时，20 m跨径、30 m跨径、40 m跨径小箱梁A级与C级平整度下的冲击系数差值最大分别为0.460、0.383、0.300，当动载试验荷载效率最大时，差值最大分别为0.362、0.264、0.220。说明随着桥面平整度越差，冲击系数越大，当动载试验荷载效率增大时，冲击系数的增大幅度减小。

(3)相同工况下的1#、2#梁，C级平整度下，当动载试验荷载效率最小时，20 m、30 m、40 m跨径的简支小箱梁两者冲击系数最大差值分别为0.050、0.112、0.100；当动载试验荷载效率最大时，最大差值分别为0.042、0.065、0.028。A级平整度下，当动载试验荷载效率最小时，各跨径简支小箱梁两片梁冲击系数最大差值分别为0.022、0.076、0.037；当动载试验荷载效率最大时，最大差值分别为0.017、0.032、0.010。说明随着动载试验荷载效率增大，相同工况两片梁的挠度冲击系数差值减小，且桥面平整度等级越高，冲击系数差值越小。

(4)速度对挠度冲击系数影响较大，但无明显规律。高速状态下，挠度冲击系数与动载试验荷载效率有呈线性变化的趋势。

3.3 简支梁桥冲击系数修正分析

3.3.1 修正系数定义分析

根据YC4-4—1978《大跨径混凝土桥梁的试验方法》中规定：

(δmax-1)ηdyn≤δ-1

(6)

式中：δmax为实测动力放大系数；ηdyn为动载试验荷载效率；δ为设计取用的动力放大系数。

该规范规定轻荷载下冲击系数取值采用动载荷载效率进行修正，但是根据本文上述研究，准设计状态的冲击系数与轻荷载的冲击系数之间的关系并不明确，其与平整度等级、速度、跨径等有关系，以此方法修正冲击系数的合理性有待商榷。

依据该规范并结合本文上述研究，且考虑对实际工程的实用原则，对轻荷载下冲击系数进行修正，建立单辆车作用下冲击系数与准设计状态下冲击系数的关系。引入修正参数ζ，ζ为考虑平整度等级、速度、跨径等因素对冲击系数影响的待定常值。基于此，提出能够便于工程应用的单辆车试验冲击系数的修正系数ηdζ。

(7)

式中：us为准设计状态下的冲击系数；uq为与准设计状态相应的单辆车的冲击系数；ηd为与准设计状态相应的单辆车的动载试验荷载效率；ζ为待定常值。

3.3.2 修正系数计算分析

桥梁动载试验通常是轻荷载在低速状态下进行，且B级平整度桥面最为常见。因此选择速度20～60 km/h，平整度等级为B级的工况，通过改变三轴载重车的载重为25 t、30 t、35 t、38 t，来模拟动载试验荷载效率的改变。选择10组平整度样本对准设计状态和单辆车作用的车桥耦合振动问题进行求解，得到挠度时程曲线，计算各工况的冲击系数后按式(7)计算各跨径ζ值。统计计算结果后，发现各跨径桥梁不同动载试验荷载效率下的ζ值在同一速度下较接近，对各跨径同一速度下的ζ值进行数据处理，剔除个别离散性较大的值后，取均值作为考虑平整度等级、速度、跨径等影响因素的修正参数ζ。

简支小箱梁桥在单辆试验车作用下的冲击系数修正系数为ηdζ，本文给出B级平整度下考虑不同影响因素的ζ值，见表5。

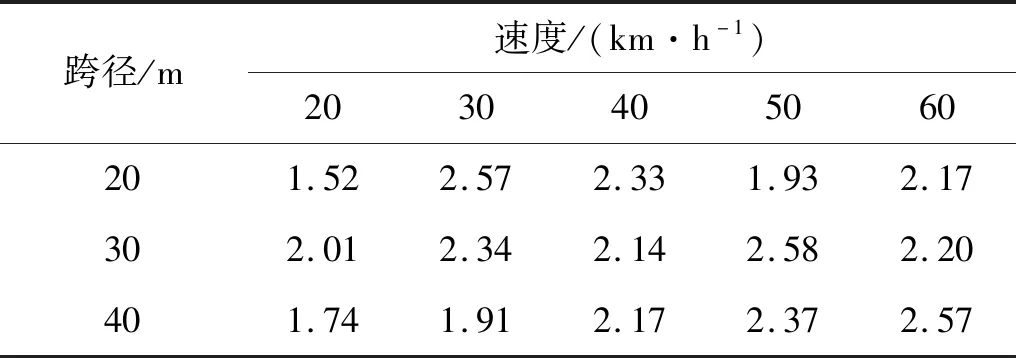
表5 各跨径简支小箱梁桥ζ平均值Tab.5 ζ average value of each span simply supported box girder bridge

由大量数据进行统计分析后得出的修正参数ζ，并结合动载试验荷载效率ηd，可得修正系数ηdζ。使用修正系数对单辆车作用下的轻荷载冲击系数进行修正，得到准设计状态下的冲击系数，即等效设计荷载作用下的冲击系数，便于对桥梁动载试验中轻荷载作用下的冲击系数进行评价。

4 结 论

本文以标准跨径的简支小箱梁桥为研究对象，采用五自由度三轴平面车辆模型，考虑了平整度、速度、跨径等影响因素，将设计车道荷载还原为等效的车辆荷载，进行了准设计状态下冲击系数的分析；分析了基于动载试验荷载效率的挠度冲击系数的变化规律，并提出了单辆车轻荷载下试验冲击系数的修正方法，建立了简支小箱梁桥轻荷载冲击系数与准设计状态冲击系数的关系。得出以下主要结论：

(1)将设计荷载的车道荷载等效还原为多辆重车荷载，进行准设计状态下的车桥耦合振动分析，结果表明按15桥规取值的冲击系数并不安全，但在桥面状况良好和低速行驶时安全性较高。

(2)整体来看，简支小箱梁桥的冲击系数随动载试验荷载效率的增大而逐渐减小，且递减速率逐渐减小。说明轻荷载容易产生更大的冲击系数，通过轻荷载所得的冲击系数直接与规范值对比评价并没有实际意义。

(3)桥面平整度状况较好时，冲击系数随动载试验荷载效率增大略有降低，随着动载试验荷载效率增大各片主梁的冲击系数相差微小或相等；桥面平整度等级较低时，冲击系数迅速增大，但动载试验荷载效率的增大会减缓其增大速率。

(4)轻荷载容易产生更大的冲击系数，因此提出了基于动载试验荷载效率的单辆车作用下的冲击系数修正方法，提出了修正系数ηdζ，此修正系数与平整度等级、跨径和车速等有关，建立了单辆车作用下冲击系数与准设计状态下冲击系数的关系，可为公路简支梁桥冲击系数的修正及评价提供参考。