自由液面对艇后螺旋桨性能的影响研究1)

2021-11-10郐云飞王世民

力学学报 2021年9期

李鹏王超韩阳郐云飞王世民

(哈尔滨工程大学船舶工程学院,哈尔滨 150001)

引言

近年来,诸多学者采用CFD (computational fluid dynamics)方法对舰艇在恶劣海况下的运动及阻力进行了研究[1-4].潜艇自身附体引发的非均匀来流会诱发螺旋桨载荷的周期性波动,进而诱发艇体结构振动而增加辐射噪声,降低潜艇自身的隐身性能[5].无线电信号在水中的传输距离有限,潜艇在必要的条件下需要靠近自由液面航行,如接收无线电信号以修正地理位置坐标,此时自由液面与非均匀来流的耦合会进一步改变螺旋桨的水动力性能,增加潜艇的生存风险,因此开展自由液面对潜艇自航模螺旋桨性能的影响研究十分必要.

螺旋桨敞水性能的研究已经取得了丰硕的成果[6-9],但关于近自由液面工作的螺旋桨的性能特性研究仍存在不足.Kozlowska 等[10-11]对吸气工况下螺旋桨的载荷变化机理进行了大量研究,认为依附在桨叶吸力面的涡结构是载荷变化的关键;Califano和Steen[12]证实常规螺旋桨的梢涡是形成吸气工况的重要因素;Paik 等[13]给出某螺旋桨近自由液面工作时上下游的速度分布及表面兴波形式;Li 等[14]和Wang[15]采用CFD 方法对在自由液面附近工作的螺旋桨性能进行了研究,发现非轴向来流会诱导螺旋桨产生明显的横向力,而斜流角度在桨叶自身压力脉动方面扮演十分重要的角色;Paik[16]就2 个尺度下的螺旋桨在近自由液面工作时水动力性能进行计算分析,并表明小尺度的螺旋桨较大尺度的螺旋桨推力损失更为严重,但2 个模型的推力损失均随着进速的增加而增大.

大量学者已经证实潜艇的阻力、升力和俯仰矩会随着潜艇自身潜深的降低而增加.Amiri 等[17]认为艇首兴波和尾肩兴波的耦合是潜艇自身水动力性能改变的主要因素,传统的假设认为:艇首兴波和艇尾兴波的耦合是潜艇自身水动力性能改变的主要因素,Amiri 等的研究结果显然和这种假设不同;Shariati和Mousavizadegan[18]对近自由液面航行的潜艇附体阻力占比进行了数值仿真研究,结果表明:附体的存在增加了约16%的黏性阻力,而兴波形式和兴波阻力并未有明显的改变;Daum 等[19]采用同Skejic和Jullumstrø[20]相同的方法来研究潜艇阻力和有效功率之间的关系;Amiri 等[21]认为带漂角航行的旋转体增加了其横向剖面的逆压梯度和流动分离,并认为自由液面和旋转体背流面的涡系耦合在水下旋转体的水动力载荷变化方面扮演重要的角色.

综上,采用CFD 方法对自由液面影响下潜艇、螺旋桨的性能研究已经取得诸多进展,但对自由液面影响下潜艇自航模及其螺旋桨性能的研究仍存在不足.本文采用CFD 方法,基于Star CCM+求解器,利用URANS (unsteady Reynolds-averaged Navier−Stokes)方程耦合k−ω湍流模型对2 个潜深、3 个航速下的潜艇自航模(Sub-off+E1619 桨)进行数值仿真计算,并分析桨前来流及螺旋桨水动力载荷变化,得到近自由液面航行潜艇自航模的流动特征及螺旋桨水动力载荷特征,以期为后续的试验研究及更细致的数值模拟分析提供参考依据.

1 数值模拟基础

1.1 理论基础

本文的数值仿真研究是利用URANS 方程耦合k−ω湍流模型开展的.连续性方程和不可压缩URANS方程的积分形式为

求解采用二阶空间离散和一阶时间离散,利用SIMPLE (semi-implicit method for pressure-lined equation) 算法对速度和压力耦合进行求解,SST(shear stress transport)k−ω[22]用于计算螺旋桨及艇体的水动力、流场信息,利用VOF (volume of fluid)法捕捉自由液面的变化.所有的计算都是在Star CCM+平台上开展的.

1.2 几何模型

本文采用的潜艇自航模是Sub-off 潜艇模型和E1619 桨的组合,具体参数及布置如图1 所示.Suboff 是一个用于学术研究的标准模型[23],有一副十字型尾舵,一个坐落在平行中体前端的流线型围壳,需要注意的是:本文选用的几何模型进行了缩放,具体的参数对比如表1,其中:Lsub为潜艇模型总长,Dsub为潜艇模型平行中体直径,Lpro为螺旋桨轴向位置,Rpro为螺旋桨半径.

图1 几何模型Fig.1 Geometry

表1 Sub-off 模型几何参数Table 1 Geometric parameters of Sub-off model

E1619 桨是CNR-INSEAN (Institute of Marine engineering-National Research Council Rome,Italy)水池提出并设计的一款潜艇用7 叶大侧斜螺旋桨,具体信息参见文献[24].一些主要的参数在表2 中列出,其中:Dpro为螺旋桨直径,Rpro为螺旋桨半径,Dhub为桨毂直径,P0.7Rpro为0.7 倍螺旋桨半径处的螺距比,c0.7Rpro为0.7 倍螺旋桨半径处桨叶剖面弦长.该桨的敞水试验是在CNR-INSEAN 的拖曳水池中进行的.为适配本文选用尺度下的Sub-off 模型,螺旋桨尺度同样进行了缩放.

表2 E1619 的主要参数Table 2 Main parameters of E1619 propeller

1.3 网格、边界条件和工况

本文设定2 种计算域:无限潜深和有限潜深,2 个计算域的尺寸和边界条件如图2,坐标系原点均位于艇体几何中心.需要注意的是:为降低兴波反射对计算结果的影响,有限潜深用的计算域较无限潜深用的计算域更大;另外,有限潜深的计算中,各边界添加波浪阻尼,阻尼波长均为4.5 m[18,21,25].

图2 2 种计算域Fig.2 Two sets of computational domain

本文采用3 套网格(粗网格、中网格和细网格) 开展收敛性研究,中网格如图3,网格信息如表3.采用切割体网格对计算域的绝大部分空间进行离散,对围壳、尾舵等附近空间进行网格细化以捕捉复杂的空间流动;艇体和螺旋桨壁面的边界层采用棱柱层网格离散,其沿壁面垂直方向以1.05 为比例逐层加厚至21 层,总厚度2 mm,由此得到壁面y+≤ 100.根据文献[25]推荐的重力波网格划分建议,在重力平行方向单个波高范围内保证25 个网格单元,重力垂直方向单个波长内保证450 个网格单元,尽管不同潜深下网格设置保持一致,但网格数量仍因艇体和自由液面垂向间距的增大形成较大的差异.螺旋桨旋转域和静止域间采用滑移网格技术进行数据交换,利用库朗数(CFL,Courant Friedrichs-Lewy)控制网格尺寸和时间步长之间的关系,CFL的定义为

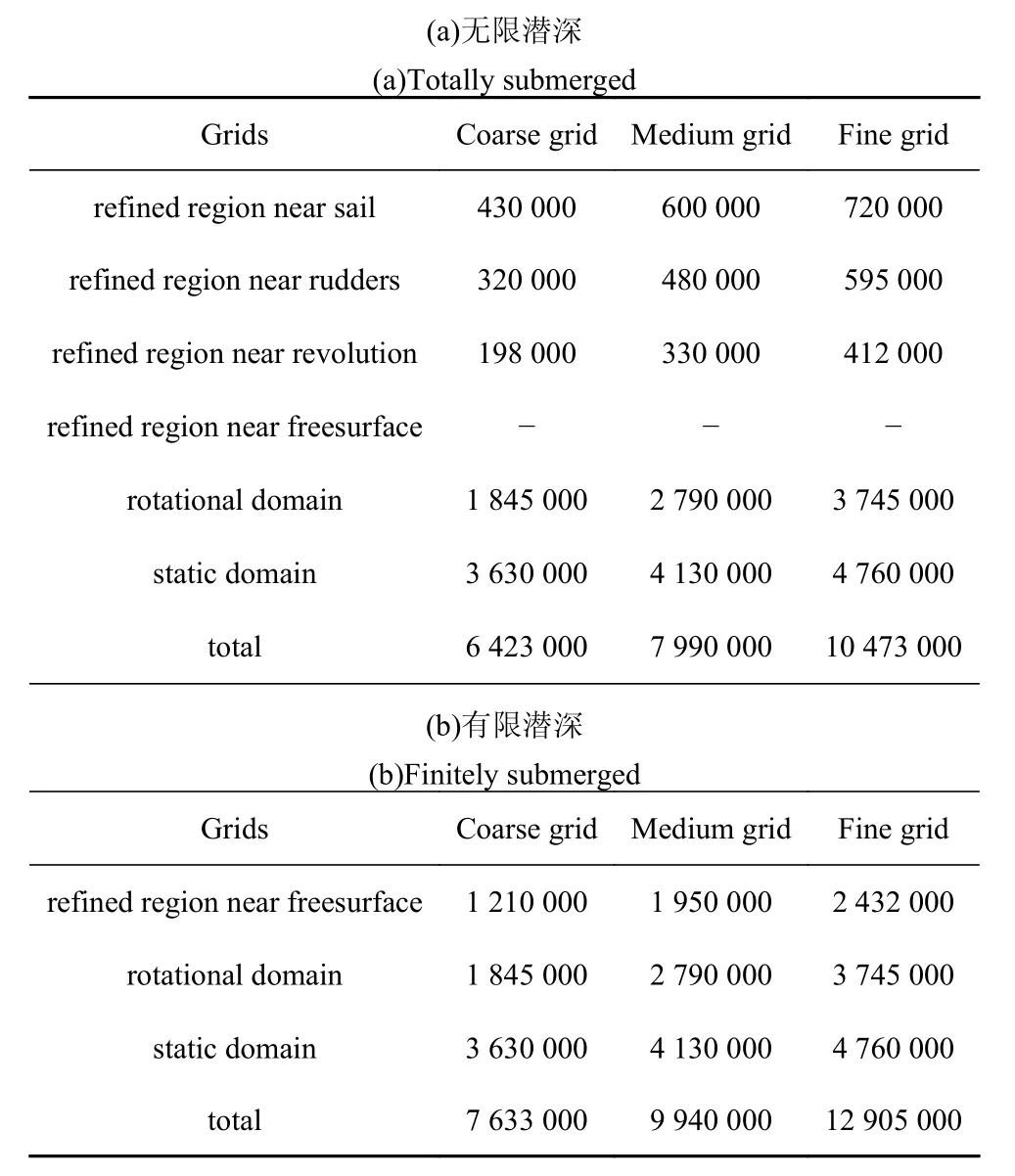
表3 不同网格方案的详细网格信息Table 3 The cells contained in various grids

图3 有限潜深条件下中网格示意图Fig.3 Grid-medium used for shallowly submerged

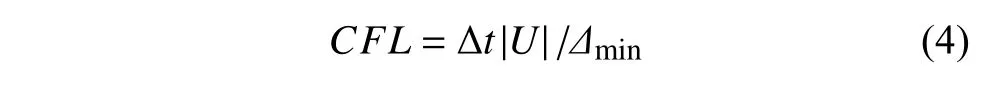
其中,Δmin为沿流向网格最小尺寸,Δt为时间步长,本文中时间步长的选取均满足CFL≤ 1.0.

参考Pan 等[26]的研究,制定如下的自航点计算流程:

(1)根据E1619 桨的敞水性能曲线和Sub-off 艇体模型的阻力曲线,在特定潜艇航速(自由来流速度)U下,依据阻力和推力相等的原则确定初始转速n0;

(2)开展至少3 个不同转速下的自航计算,获取对应转速下螺旋桨的推力和艇体阻力,并绘制螺旋桨推力、艇体阻力随转速变化的曲线;

(3)在第(2)步中获得的2 条曲线的交点对应的转速即自航模在对应航速下的螺旋桨转速,即自航点.

重复上述步骤完成设定的2 个潜深、3 个航速下的自航模计算,具体的工况信息如表4,其中H为潜艇航行潜深,U为自航模的航速或自由来流的速度.

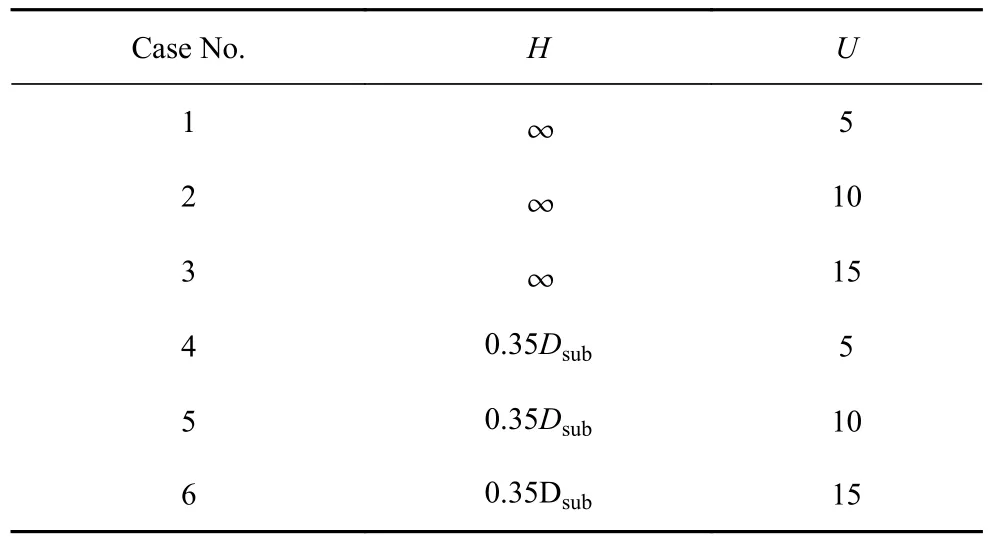
表4 计算工况信息Table 4 The cases listed in this paper

2 验证或确认

2.1 数值方法的验证

本文数值方法的正确性是通过对比数值结果和实验结果来确认的,对比的实验结果包括:标准Suboff 模型的阻力实验;不同潜深下的旋转体阻力实验;E1619 桨敞水实验.上述实验均可在文献[27-29]中查阅.用于数值模拟方法验证的网格信息如表5 所示,具体网格见图4,需要注意的是:Sub-off 标准模型的网格划分和1 小节中网格划分策略相同,差异仅体现在模型和计算域的尺度上,其它2 种数值方法验证的模型尺度均和文献中相同.

图4 部分验证网格示意图Fig.4 Sketch of the grids used for validation

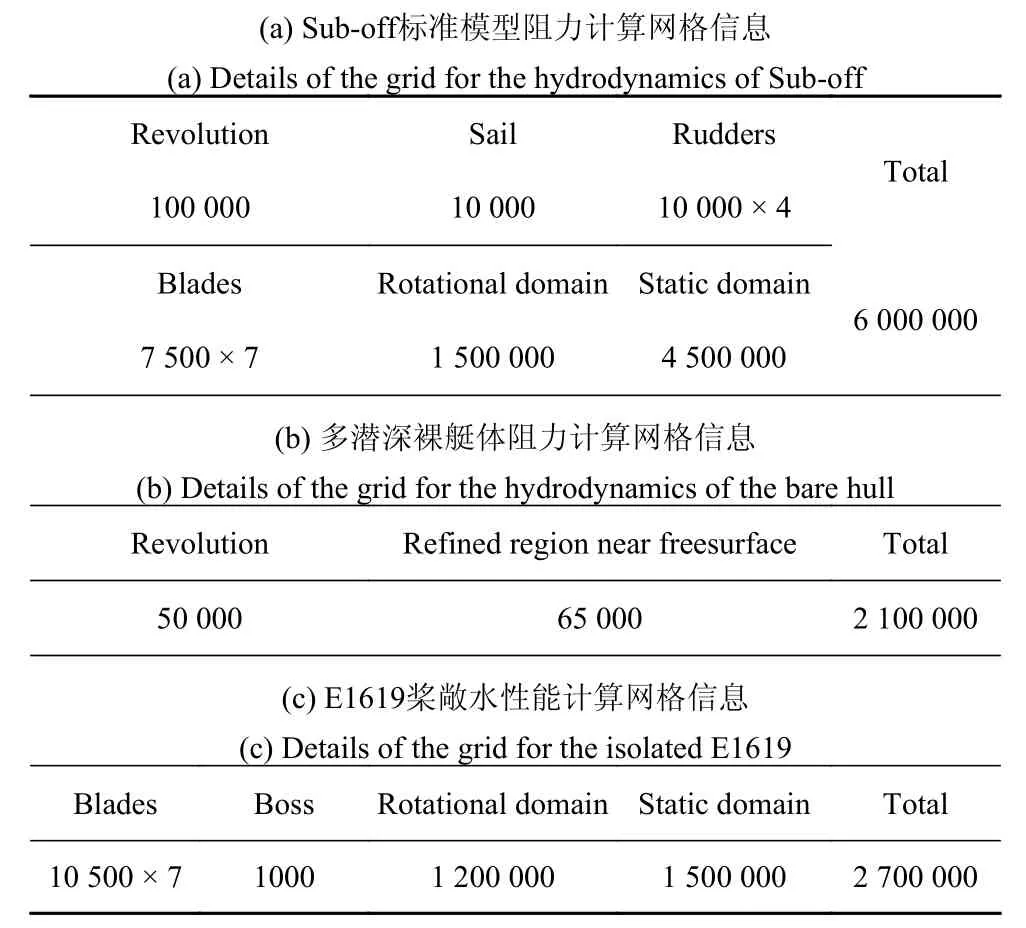
表5 数值模拟方法验证网格信息Table 5 Characteristics of the grids used for validation

阻力计算结果如图5 所示,数值模拟结果和实验结果取得了良好的吻合,但数值模拟低估了Suboff 模型在高航速下的阻力,推测是采用的网格不足以精确捕捉如此航速下的流动特征;基于不同的相似准则(有限潜深:等傅汝德数、无限潜深:等雷诺数)得到标准Sub-off 模型的航速均低于本文验证工况中选用的最大航速;同时本文选用的验证工况最大航速为6.68 m/s,且数值模拟结果和实验结果误差为4.23%,在合理的误差范围内;综上,可以确定本文采用的数值仿真方法能保证计算结果的正确性.

图5 全附体Sub-off 模型阻力-航速曲线Fig.5 R-U curve of the all-appendage Sub-off

通过对比E1619 桨的仿真结果和敞水实验结果,如图6 所示,其中CT,CQ和η分别是螺旋桨的推力系数、扭矩系数和效率,定义分别为

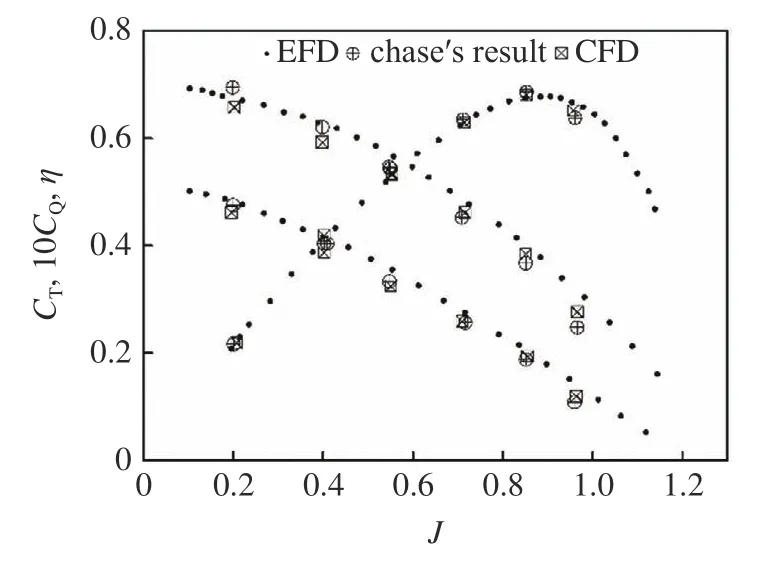
图6 E1619 桨敞水曲线Fig.6 The OWC of the E1619

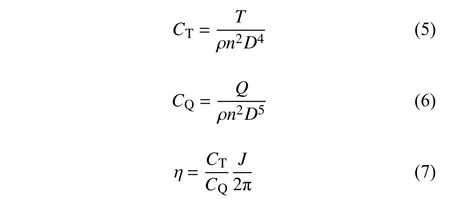
式中,T为推力,Q为扭矩,J=U/(nD)为进速系数.可看出,两者在进速系数为0.2～ 0.9 的范围内吻合良好,由此推断,本文采用URANS 方程结合k−ω湍流模型能准确地预报螺旋桨的水动力性能.Amiri等[17,29]开展不同潜深、航速下的旋转体阻力实验,结果见表6,本文采用相同的模型,对相同工况下的旋转体进行了数值仿真计算,结果亦列在表6 中,可以看出,不同的傅汝德数(g为重力加速度,9.81 m/s2)下本文的计算结果几乎和实验结果一致,进一步证实数值模拟方法的正确性.

表6 旋转体不同潜深、航速下地阻力系数(扩大1000 倍)Table 6 1000 × CR of the revolution with various depths(The results from this paper are in backets)

上述所用工作的开展均证实数值模拟方法模拟自航模在近水面航行的可行性和正确性,因此本文后续的计算均采用URANS 方程结合k−ω湍流模型的方法开展数值仿真计算.

2.2 网格收敛性验证

为了评估第1 节中提及的3 套网格方案的收敛性,本文针对潜深为1Dsub,航速为10 kn 的自航模进行了重复计算.基于前人的研究成果[30-34],本文制定了网格收敛性计算过程.首先,定义网格收敛性系数RG为

式中,Si是分别是3 套网格方案的计算结果,其中i=1,2,3 对应了粗网格、中网格和细网格;接着,参考Roache[31]的研究,利用广义理查森外推法来评估网格不确定性并定义hi为

式(12)中 εG32是细网格和中网格计算结果的差异(S3−S2).3 套网格方案得到不同的计算结果如表7和表8 所示;接着,对表7 和表8 中的数据进行不确定性分析后得到网格不确定度的评判因子结果,并列出在表9 和表10 中;需要说明的是,当遵循上式计算得到的PG大于2 时,取PG=2 进行UG的计算.可以看出得到的UG均非常小,证实数值模拟结果对本文采用的空间分辨率均不在敏感,而采用中网格方案能保证计算效率和结果的优异性,因此后续的计算均采用中网格开展.

表7 有限潜深艇体计算结果Table 7 Hydrodynamics of the sub-off navigating finitely submerged

表8 有限潜深螺旋桨推力及扭矩系数Table 8 CT and CQ of the propeller attached at the stern of the Sub-off navigating finitely submerged

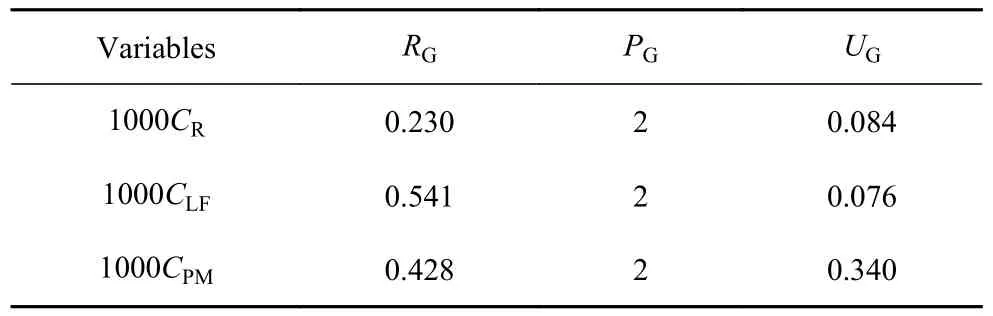
表9 有限潜深艇体计算结果Table 9 Hydrodynamics of the Sub-off navigating finitely submerged

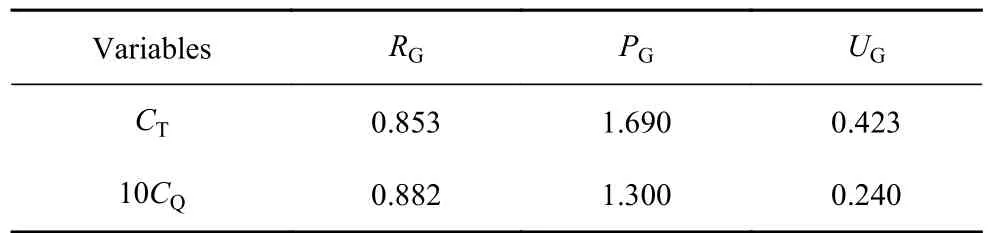
表10 有限潜深螺旋桨推力及扭矩系数Table 10 CT and CQ of the propeller attached at the stern of he Sub-off navigating finitely submerged

3 结果与讨论

3.1 自航点的确认

依据1.3 节介绍的自航点计算方法,对2 个潜深,3 个航速下的Sub-off+E1619 桨潜艇自航模的自航点进行计算,针对每个工况自航点的确认开展至少3 个螺旋桨转速的计算,最终通过线性插值得出对应潜深和航速下的自航点(螺旋桨转速,nself),计算结果如表11.固定潜深,随着航速的增加,自航模的自航点转速不断增加;相同航速,随着潜深的降低,自航点对应的螺旋桨转速增加,对比发现,增幅对航速更为敏感.根据Amiri 等[17]的研究,不同航速下,艇首兴波和尾肩兴波的耦合是改变潜艇阻力的重要原因,数值计算得到的结果也表现出这种本质相同的变化.表12 给出不同航速和潜深下,Sub-off模型平均阻力系数和E1619 桨平均推力系数的计算结果,图7 是自航模的艇体阻力系数和螺旋桨推力系数基于对应基准(完全浸没深度下的阻力系数和推力系数)的变化.不同航速下艇体阻力系数随航速增加而降低,推力系数亦如此.总结来说,自由液面的存在会增加潜艇自航模自航点对应的螺旋桨转速,且这种改变对潜艇航速更为敏感;自由液面的存在对艇体阻力系数的改变是规律且单调的.

表11 自航点计算结果Table 11 Self-propulsion

表12 艇体和螺旋桨平均水动力系数Table 12 The mean hydro-coefficients of hull and propeller

图7 艇体和螺旋桨的水动力系数变化Fig.7 The changes of hydrodynamic loads of hull

3.2 自由液面对全局流场的影响

图8 表明兴波(中纵剖面和自由液面的交线)随航速的变化,不同工况下波峰始终位于艇首附近,而在艇体平行中体结束前的波高均不断下降,推测波谷处于平行中体末端附近,图8 中航速为5 kn 时在艇长范围内均出现了完整的半个兴波(从波峰到波谷),但其他2 个速度均未出现,换言之,随着航速的增加兴波长度不断增加.根据Amiri 等[17]和Shariati和Mousavizadegan[18]的研究,艇首高压区形成的以波峰起始的波系和尾肩低压区形成的以波谷起始的波系相位耦合主导了近自由液面航行潜艇的整体兴波模式,本文的计算结果恰好同样证实了这样的波系产生.图9 是不同潜深艇体纵剖面流场速度变化云图,图中V是流场内的当地轴向速度,近自由液面航行时,自由液面通过蓝色虚线标注出来,同时将艇体周围流场主要分为围壳尾流区(蓝色虚线框)、尾舵尾流区(黑色虚线框) 和艇首流动区(绿色虚线框),可以明显看出,自由液面对艇首流动影响十分微弱,艇首区域流动主要受前端驻点和有利的压力梯度控制,随着流动沿艇体表面的演化,边界层加厚,垂直纵剖面(图9(a))和水平纵剖面(图9(b))均表明这一特征;Chase等[35-36]认为尾舵尾流的存在会改变螺旋桨尾流梢涡的对称螺旋面形状,图9 中螺旋桨尾流的上下流速的差异证实这样的观点.兴波波幅沿流向起伏变化,造成自由液面与潜艇壁面间距变化,基于Ponkratov[37]的假定,可推断,围壳尾流的流速存在差异;同理,尾舵尾流的流速亦有不同,定性来看,螺旋桨载荷增加是桨前来流速度降低造成的.Amiri 等[17]和Shariati 和Mousavizadegan[18]的研究认为潜深降低会增加潜艇阻力,艇体的低压区诱发边界层加厚,进而增加艇体阻力.对比图10 可知,兴波模式显然对航速更为敏感,围壳尾流、尾舵上梢涡和螺旋桨尾流受制于兴波波幅梯度,螺旋桨尾流与艇体中心轴线的夹角变化证实这样的说法,同时,图中红色箭头标注的区域表明:流速的变化与波高成反比,即较低航速下的兴波模式显著降低自由液面和艇体表面的间隙,进而使得这一区域的流速增加.

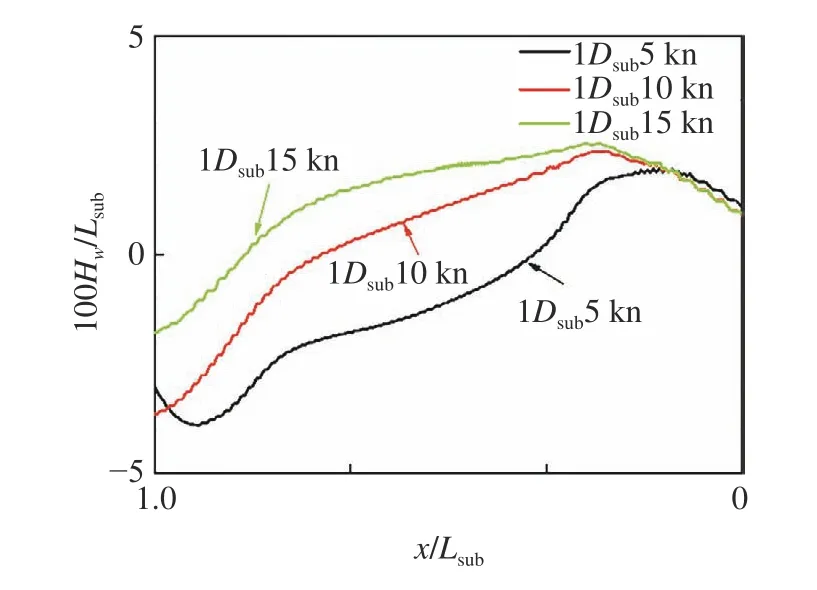
图8 兴波模式Fig.8 Wave pattern

图9 15kn 航速不同潜深下艇体周围流场Fig.9 The flow field around Sub-off at 15kn under various depths

图10 潜深1Dsub 时不同航速y=0 平面流场Fig.10 The flow field around Sub-off navigating under 1Dsub from the free-surface with various velocities

3.3 自由液面对桨前来流的影响

自由液面的存在增加桨前来流的轴向速度,并且随着航速的降低自由液面的影响会增加,这一点在图11 和表13 中可以明显看出;桨前来流似乎未因为螺旋桨的旋转出现抽吸加速,反而有阻碍来流速度增加的趋势,如图11 中蓝色虚线内的流动;总之,自由液面的影响会随着潜深、航速的增加而不断削弱.

表13 螺旋桨近前方轴向伴流分数(wi)Table 13 The mean axial wake fraction (wi) before propeller

图11 螺旋桨近前方轴向速度云图Fig.11 The axial velocity before propeller

图12 是桨叶剖面的速度三角形示意图,图13所示的螺旋桨近前方来流下0.7Rpro处的来流攻角(α)曲线;来流攻角呈现周期性的变化,变化周期对应桨叶的通道时间,图11 也清晰地表明这一点,同时随着潜深的降低波动的幅度也有略微的削弱,尽管自由液面的影响随着潜深的增加而降低,但是桨叶在靠近自由液面的过程中(即0°～ 90°)自由液面仍然一定程度上加剧攻角的波动变化,如图13(b)、图13(d)、图13(e)所示;桨叶攻角对潜深十分敏感,需要强调的是:波动滞后的原因是本次计算中并未校准桨叶旋转的起始位置,但这并未影响对结果的讨论.

图12 桨叶剖面速度三角形Fig.12 The velocity triangle in blade profile plane

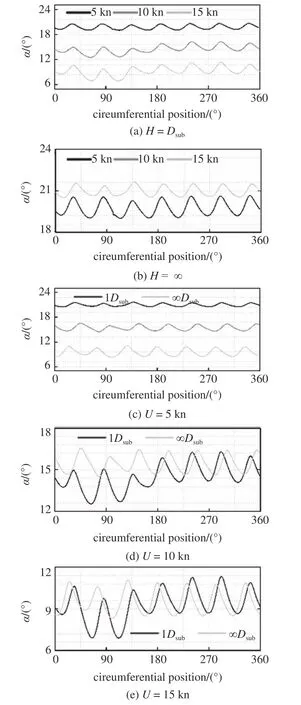
图13 0.7Rpro 桨叶攻角变化Fig.13 The attack angle (α) at 0.7Rpro

图14 是桨前0.7Rpro处来流径向速度的周向平均变化曲线,可以看出小潜深、低航速工况下自由液面加剧径向速度的径向变化,参考文献[37]的假定:变形后的自由液面和艇体表面设定为壁面条件,变形的自由液面参见图9(a)和图10,则桨盘面前后的流场形成了类似喷嘴的结构,而图14 中径向速度沿着螺旋桨径向的突起变化也符合喷嘴内流场的速度变化[38],而潜深的变化会改变表面兴波的变化,图9(a)中,1D潜深、5 kn 航速时,自由表面的变化最为剧烈,从而使得喷嘴的收缩率增加,流速增加,自由表面变形逐渐平和,即喷嘴的收缩率降低,对应图14 中径向速度的急剧向无限潜深工况靠近;而潜深增加会从量级上增加喷嘴收缩率的变化,换言之,收缩率对潜深的变化更为敏感;此处的假设同时也可以解释桨前来流轴向速度增加.

图14 螺旋桨近前方0.7Rpro 处来流径向速度周向平均曲线Fig.14 Circumferentially averaged radial velocities before propeller at 0.7Rpro

无限潜深工况下,艇体尾部几何形状的收缩会使得桨前来流的边界层加厚,近壁面的涡量也会增加,而桨前涡流被十字型尾舵划分为4 个涡流集中区域,如图15 中黄色虚线标注所示,而桨叶诱导作用对桨前来流的涡流变化十分微弱,航速的变化主要是增加围壳对桨盘面尾流涡量的影响,根据文献[39]的研究可知,航速的增加主要是增加马蹄涡的强度,从而增加其影响范围;潜深的降低主要增加桨叶的抽吸作用或诱导作用,而这一抽吸或诱导作用会抑制艇体尾流/桨前来流的涡量幅度,使得桨前来流趋向均匀化、无旋化;值得注意的时,桨前来流靠近自由液面的部分涡量在相同潜深下较远离的部分更强,旋度更大.

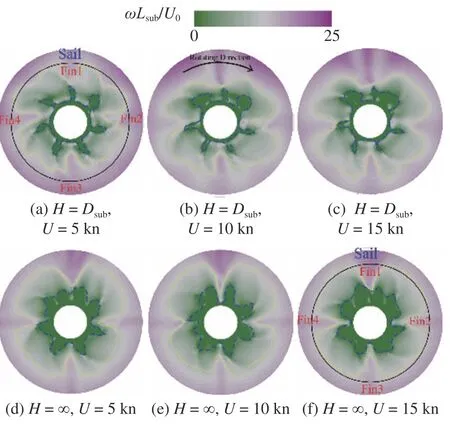
图15 螺旋桨近前方涡量云图Fig.15 The ω before propeller

总之,随着潜深的降低,艇体尾流伴流会急剧降低,从而增加螺旋桨桨叶剖面的来流攻角,在特定的假定条件下,桨前来流的速度变化规律同喷嘴内流的速度变化有相似之处;桨前来流的涡流成因主要是艇体尾部几何曲率增造成的边界层加厚,尾舵或螺旋桨的抽吸作用抑制了来流涡旋的产生,而自由液面刚好起到相反的作用.

3.4 自由液面对螺旋桨性能的影响

本节对3 个连续的单独桨叶进行力学分析,并截取自计算收敛后螺旋桨旋转30 圈的数据.桨前来流的不均匀性造成桨叶载荷的时历波动,由于数据量足够大,3 个桨叶的统计结果基本一致.桨叶1 的详细信息如表14 所示.

表14 单个桨叶水动力载荷的统计学结果Table 14 The statistics of hydrodynamics act on single blade

无自由液面影响的情况下,随着航速的增加,单个桨叶的推力系数随着航速的增加而降低,从0.033 4降至0.029,同时推力的波动有所增加;扭矩系数的变化微弱,由此可见艇后螺旋桨扭矩对航速的变化较为敏感,而航速的增加会降低扭矩波动的剧烈程度;自由液面的存在增加了扭矩系数、推力系数及其波动程度,根据Amiri 等[17]和Shariati 和Mousavizadegan[18]研究,航速较潜深而言对兴波模式的影响更大,表14 中推力系数随航速的增加而降低,但自由液面的影响使航速为10 kn 下螺旋桨的推力系数大于其它2 个航速,证实Amiri 和Shariati 等研究中的假设.

以单个桨叶旋转一圈为周期,对其旋转30 圈的时历结果数据进行平均,结果绘制如图16 所示.自由液面的存在改变了桨叶旋转周期内的载荷波动频率,潜深为Dsub时,桨叶载荷在旋转周期内明显被划分为两个子周期,如图16(a)、图16(c)、图16(e)所示,在有限潜深下,载荷与桨叶旋转位置有关;定性来看,随着航速的增加,单个旋转周期内,桨叶载荷的均值降低,载荷极值差异增加.无限潜深条件下,无自由液面的影响,单个旋转周期内,单个桨叶载荷可分为4 个子周期,即4 个尾舵尾流将螺旋桨桨前来流划分成了4 个伴流区,如3.3 节中图15 所示,另外需要注意得是,尾舵1 尾流造成桨叶载荷极值更大,由此推断围壳尾流叠加尾舵1 尾流诱发经过这一区域的桨叶载荷极值和波动幅值增加.

图16 单个桨叶载荷旋转周期平均曲线Fig.16 Circle-average blade hydrodynamics

图17 是单个桨叶旋转30 圈内推力系数时历数据的谐波分析,航速为5 kn 时不同潜深对应的基波频率(k)分别为:12.7 Hz (工况1)、19.2 Hz (工况4);航速为10 kn 时不同潜深对应的基波频率分别为:25.0 Hz (工况2)、27.65 Hz (工况5);航速为15 kn时不同潜深对应的基波频率分别为:36.65 Hz (工况3)、42.07 Hz (工况6);随着航速的增加,基波频率略微增加,但是基波对应的推力系数幅值发生了显著变化,无自由液面的影响时,除1 次谐波外,航速对其它推力系数的谐波幅值影响微弱;自由液面的存在显著的改变了各谐波下推力系数的幅值,航速的增加,尾舵和围壳的脱落涡流频率改变,从而增加推力系数谐波频率和幅值[40].

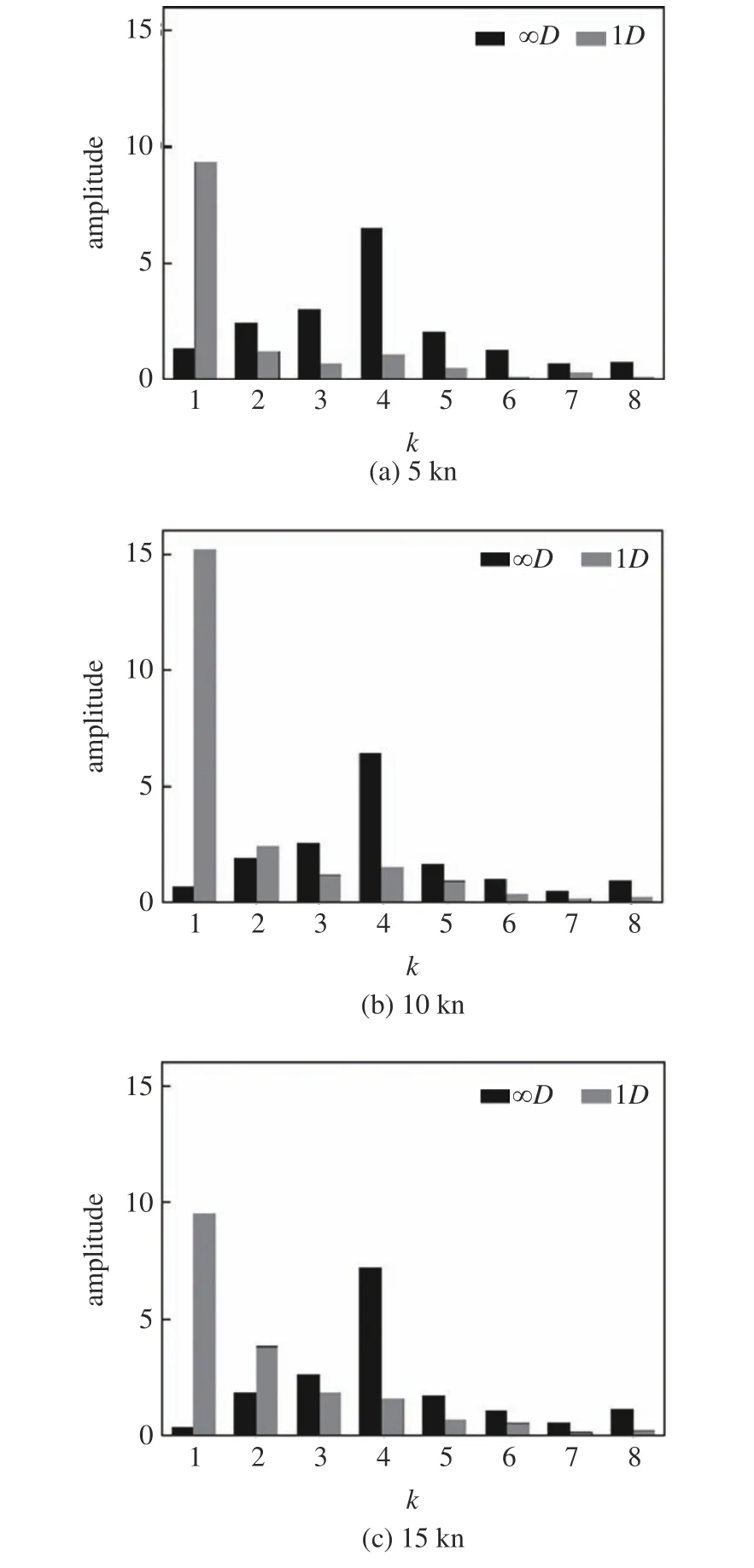
图17 单个桨叶时历载荷的谐波分析Fig.17 Harmonic analysis of hydrodynamics of single blade

图18 为自由液面波高(Hw)沿横向的变化以及桨叶表面压力分布,自由液面显著改变桨叶表面的压力分布,而桨叶推力的产生主要依赖叶面和叶背的压力差,对比可知,桨叶压力面对潜深的敏感性更大,而吸力面对航速和潜深均不太敏感,对比图8:当航速为5 kn 时,小潜深工况下,螺旋桨位于兴波从波谷向波峰的过渡区,换言之,自由液面处于斜向上发展,且潜深增加,斜率降低;而航速为15 kn 时,兴波发展趋势则相反,即兴波从波峰向波谷发展,并且随着潜深的增加,兴波斜率降低,根据文献[37]的假定可推断,艇后螺旋桨的环境压力与兴波变化密切相关,螺旋桨的推力系数变化趋势便同表面兴波紧密联系起来.图18 中,单一桨叶在旋转周期的不同的相位位置处液面压力分布有些许差异,诚然这与尾舵尾流耦合艇体尾流形成的螺旋桨非均匀来流有关,但更为明显的是靠近自由液面和远离自由液面对桨叶表面的压力分布起到更明显的影响作用.另外,螺旋桨上方自由液面明显呈楔状分布,随着航速的增加,螺旋桨上方波幅降低,对应3.2 节中兴波相位随航速变化的趋势,更有效的证实了桨叶表面压力分布与兴波分布的密切关系.

图18 横向兴波模式和桨叶表面压力系数Fig.18 Wave pattern and CP in blades

表15 是不同航速和潜深工况下螺旋桨的水动力载荷结果,对比不同航速、不同潜深工况下螺旋桨水动力载荷的波动情况,发现载荷波动未因航速、潜深的变化发生显著增加或降低,但扭矩系数和侧向力系数因潜深的降低发生显著的增加,由此可知,螺旋桨扭矩系数和侧向力系数较推力系数对潜深更为敏感;对比单个桨叶的推力系数变化,螺旋桨的推力系数随着航速的增加而降低、随着潜深的降低有所增加,这与单个桨叶的水动力载荷变化基本吻合,但是不同于单个桨叶推力系数在航速为10 kn时的异常凸点,螺旋桨推力系数仅在无限潜深时存在推力系数的凸点,由此可以推断,螺旋桨推力系数随着航速的变化是非线性的,而自由液面的存在削弱了螺旋桨推力系数与航速间的非线性关系,这种改变的动力来源于桨叶在旋转周期内靠近和远离自由液面时带来的推力系数变化,结合图16 中随着潜深降低,桨叶旋转周期内的子周期分布可知.