基于相空间重构的滑坡位移时间序列预测
2015-10-08孙九兵王珊珊
孙九兵 王珊珊

【摘 要】本文基于滑坡时间序列位移,根据相空间理论构建位移时间序列矩阵,利用熵值理论求取熵值。通过熵值变化及位移预测误差反馈调整该时序相空间重构的嵌入维数,然后利用支持向量机学习创建支持向量回归机模型。并通过实例进行位移时间序列预测,预测效果好。
【关键词】滑坡;时间序列;相空间
0 前言
在对滑坡的位移演化研究中,由于滑坡的形态、类型、规模等各不相同,一般选择单个滑坡研究其位移时间曲线的变化。在传统的位移时序研究方法[1-2]中,是采用时间序列分析法直接从位移这个序列研究滑坡的时间演变。随着滑坡可以被视为一种具有混沌特征的复杂过程这一观点的提出,根据混沌系统特征预测滑坡位移可能比统计学方法的预测更好[3]。相空间重构理论是混沌时间序列预测的基础。在滑坡这个受地质条件、地下水、地震和人类工程活动等多种因素影响而发展演化的多维非线性动力系统中,位移作为滑坡变形破坏的重要反馈信息,包括整个系统的非线性动力特征,通过位移数据的相空间重构可体现整个系统的运动特征。
1 相空间重构理论
1.1 滑坡位移时间序列相空间
相空间重构理论系统中分量之间存在着相互作用,并且任一分量的变化与其他分量之间不可分割,这些分量的信息也可以说就隐藏在任何一个分量的变化过程中[4-5]。因此系统的混沌行为可以通过系统长期演变的任一单变量时间序列来研究[6]。
对滑坡位移时间序列重构相空间,引入延迟时间和嵌入维,建立恰当的模型,根据一维位移序列转换出多维的相空间,可研究滑坡位移系统的动态特征[7]。
1.2 嵌入维
记逆序重构的相空间转置矩阵为时序重构矩阵(1),取m为整数N/2,则该矩阵包括所有的样本。
a)为方便计算,首先对重构的位移时间序列矩阵按照原序列按照自底向上的顺序进行扩充,并在空白位置填补零值。令dij表示扩充后位移时间序列矩阵中第i行第j列的位移记录值,则根据熵值理论的要求,其熵值计算如式(2),式中,k是一个常数1/In(l2),l1,l2分别为扩充后位移时间序列矩阵的行数和列数。并且当pij=0时,则令In(pij)=0。
b)找出峰值点对应的维数。定义在熵值变化量曲线中的任意三个连续维数,如果中间维数对应的值大于两端维数对应的值,则称中间维数对应的熵值变化量为峰值,中间维数为峰值维。即先对上式(2)中求得的熵值求取其变化量,再从中寻找峰值对应的峰值维,如式(3):
Fi=max{(hi-hi-1),(hi+1-hi),(hi+1-hi)},i∈{1,2,…,l2}(3)
其下标i就是峰值点对应的峰值维。根据这个维数可以重新构建相空间位移时序矩阵作为模型的训练集。如果峰值维只有一个,则可以唯一确定相空间重构维,否则需要根据多个峰值维以相同的方式分别建立位移时序预测子模型,并计算子模型的均方根误差,选取均方根误差最小的峰值维作为整个序列的重构嵌入维数。
2 支持向量机
支持向量机[8-9]是一种比较好的实现了结构风险最小化思想的方法,对给定的数据逼近的精度与逼近函数的复杂性之间寻求折衷,以期获得最好的推广能力。从理论上说,支持向量机解决了在神经网络方法中无法避免的局部极值问题,并将实际问题通过非线性变换转换到高维的特征空间,在高维空间中构造线性决策函数来实现原空间中的非线性决策函数,巧妙地解决了维数问题,并保证了有较好的推广能力[10-11]。一般采用回归在边坡位移非线性时间序列中预测期位移值[12]。
3 模型建立
Oracle Data Mining (ODM) 强大的数据挖掘功能以 Oracle 数据库中的原生 SQL 函数形式提供[13]。Oracle SVM会基于算法的复杂度及样本不大的原因自动取样来实现线性扩展[14]。但在创建模型之前,为了满足数据的平稳性,还需要进行趋势移动、目标转换、属性选择数据处理。
3.1 数据处理
采取对已知观测数据序列进行对数变换可以在一定程度上减小不可观测的误差和预测变量的相关性,差分可以消除其趋势以及降低其波动幅度,Z-score方法的常态化可以使其在零值附近波动而成为平稳序列,即tdi=log(di),tdi+1=tdi+1-tdi,tdi=(tdi-td)/σtd,其中td,σtd分别为参与模型训练的样本均值及方差。
3.2 模型建立
ODM通过PL/SQL API等接口的调用可以实现数据挖掘的建模、测试及应用模型等基本功能,并为多种数据挖掘算法提供支持[15-17]。其中ODM SVM回归支持通过时间延迟或lag方法的时序建模,提供时序预测功能,但是训练更简化。在其简单的形式中,以时序想要预测内容作为目标,目标的过去值被作为模型的输入。
在滑坡的位移时序模型建立中,其位移是模型预测的目标,而位移样本数据则会预留小部分作为检验数据,其余数据则作为位移过去值成为模型的输入部分。单变量位移序列通过时序重构矩阵变换后则构成模型的训练集。这一过程不仅使单变量的序列从一维扩展到了多维,还给加入其他影响因素提供了机会。鉴于位移数据的非平稳性,在训练模型之前还需要经过一系列的数据处理。然后通过在处理后的训练集上利用PL/SQL API训练创建SVR数据挖掘模型。同时利用得到的模型进行多步预测,并对预测结果经过与数据处理相反的还原操作后得到预测的位移序列后n个时刻的实际预测值。
4 以白家包滑坡为例
4.1 数据准备
本文以库区三期监测滑坡的秭归白家包滑坡作为研究对象。滑坡体上共布置有4个GPS监测点。监测时间始于2006年。对滑坡地表观测原位移数据通过样条差值处理得到65个观测数据,整个数据分为两部分,第一部分取前59个为观测样本数据,剩余数据组成第二部分,作为检验数据。对数据进行分析发现:监测数据都与时间有关,具有一定的连续性,适合采用回归算法以及拟合算法来建立模型。
4.2 相空间定维
时序重构矩阵的变换与相空间重构维数密切相关。而在相空间中,其维数直接关系到时间演变因子与其他因子的各种相互作用,因此,维数的确定是重构的一个关键。
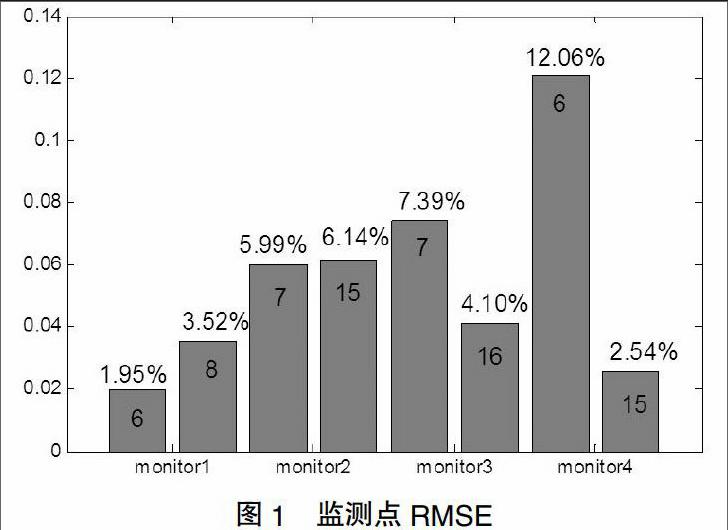
在本实例中,4个监测点的位移时序分别使用相同的方式进行处理及预测。首先利用单个监测点等距处理后第一部份的54个样本初次确定时序重构矩阵,其重构时延默认为1,维数初值是样本数的一半为27。然后根据变换得到的时序重构矩阵求取其熵值信息。在熵值信息中可以发现,噪声的影响会随着维数的扩大而增加,且各个监测点位移序列得到的熵值大小相差不大。因此,我们需要选择一个合适的范围进一步观察。当本实例中的熵值大于0.85时,其对应的维数不仅满足相空间维数确定的经验赋值法,而且也符合时间序列所代表活动先验知识中选取维数的范围。故主要处理熵值大于0.85时的部分,进一步求取其对应熵值与相邻维对应熵值差的绝对值作为该维对应的熵变化量,从而确定熵变化量曲线。再根据熵的变化量曲线寻找其峰值维的过程中,发现每个监测点分别包含2个维数待定选项。为了确定最终的维数,则先以样本数据第一部分的子集作为输入,根据这些维数分别以相同方式建立子模型并求取其RMSE。
不同维数最终得到的预测值之间存在明显差异,为尽可能预测其变化趋势,需要根据误差反馈进一步调整维数。选择其误差最小时对应维数作为该序列的合适重构维数,即4个监测点位移分别确定维数为6,7,16和15。
4.3 滑坡位移时间序列预测
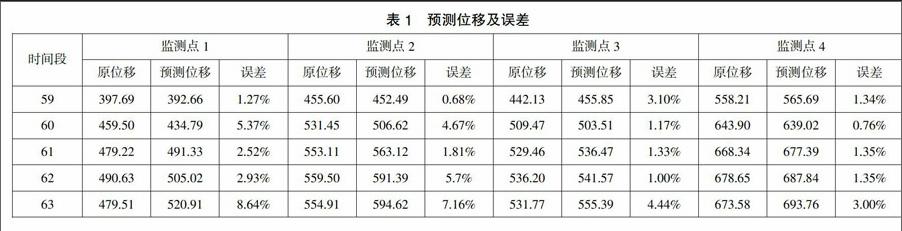
各个监测点观测序列分别利用最终确定的嵌入维数重复位移时间序列矩阵构建过程,从而使原始的一维序列通过变形得到用于短期预测的学习样本。通过对学习样本的训练得到支持向量机时序预测模型,并以检验数据以外的所有样本作为模型输入,模拟后续情况下的位移时间序列预测。其预测值同样需要经过与数据处理过程完全逆向的还原操作。各个监测点的预测结果(如表1所示)与原位移相对接近,前四步的误差均保持在6%以内,预测效果较好。
5 结束语
从理论上说,相空间重构中的嵌入维数选择越大越好。但随着嵌入维数的增大,其噪声的影响也会放大,因此需要选择合适的嵌入维数。但用于相空间重构的维数也不可能不断扩大,在实际中往往需要一个学习效果好且相对稳定的模型进行预测。对比发现,基于熵值理论寻找的维数通过重构后训练集的预测效果拟合较好,能够提高一定的准确性。从而说明,熵值理论对寻找合适的相空间嵌入维可能会有帮助。另外,SVM回归提供的时序预测功能训练简化,能够使用大量变量,因此被广泛应用于金融预测、电力负载预测等很多领域。
【参考文献】
[1]徐峰,等.基于时间序列分析的滑坡位移预测模型研究[J].岩石力学与工程学报,2011,30(4).
[2]彭令,牛瑞卿,吴婷.时间序列分析与支持向量机的滑坡位移预测[J].浙江大学学报:工学版,2013,47(9).
[3]周创兵,陈益峰.基于相空间重构的边坡位移预测[J].岩土力学,2000,21(3).
[4]吴湘宁,胡炫,胡光道,胡成玉,李桂玲.Oracle 中使用支持向量机的时间序列预测方法[J].计算机工程与应用,2013,49(14):121-125.
[5]唐璐,齐欢.混沌和神经网络结合的滑坡预测方法[J].岩石力学与工程学报,2003,22(12):1984:1986.
[6]刘华明,齐欢,蔡志强.滑坡预测的非线性混沌模型[J].岩土力学与工程学报,2003,22(3):434-437.
[7]杨虎,吴北平,汪利.混沌序列PSO-RBF耦合模型在滑坡位移预测中的应用[J].科学技术与工程,2013,13(30).
[8]刘华煜.基于支持向量机的机器学习研究[D].大庆石油学院,2005.
[9]林大超,安凤平,郭章林,张立宁.滑坡位移的多模态支持向量机模型预测[J].岩土力学,2011,4(32):451-458.
[10]熊天安,刘邦兵,雷畅.相空间重构理论支持下的滑坡预测方法[J].地理空间信息,2011(3).
[11]董辉,傅鹤林,冷伍明.支持向量机的时间序列回归与预测[J].系统仿真学报,2006,18(7):1785-1788.
[12]刘开云,乔春生,滕文彦.边坡位移非线性时间序列采用支持向量机算法的智能建模与预测研究[J].岩土工程学报,2004(1):57-61.
[13]陈荣鑫,陈维斌.基于Oracle ODM的数据挖掘研究[J].微机发展,2005(7):84-85.
[14]刘维会.不平衡数据集上支持向量机算法研究[D].山东科技大学,2010.Liu weihui. Study of Support Vector Machine Algorithms on Unbalanced Dataset. ShandongUniversityofSeienceandTechnolog,2010.
[15]朱传华.三峡库区地质灾害数据仓库与数据挖掘应用研究[D].中国地质大学,2010.
[16]http://blog.csdn.net/wonder4/article/details/1919156[Z].
[17]Oracle USA, Inc. Oracle data mining application developers guide 11g release 1 (11.1), B28131-04[R]. CA, USA: Red-wood City, 2008[Z].
[责任编辑:汤静]
