基于比例加速退化建模的单台机载设备剩余寿命自适应预测
2021-11-10蔡忠义王泽洲陈云翔项华春王莉莉
蔡忠义, 王泽洲, 陈云翔, 项华春, 王莉莉
(1.空军工程大学装备管理与无人机工程学院, 陕西 西安 710051;2.中国人民解放军93920部队, 陕西 汉中 723200)
0 引 言
出于保证飞行安全和任务完成的需要,机载设备普遍具有高可靠、长寿命等特点,导致传统寿命试验和退化试验难以快速地获取足够的寿命/退化数据来确保剩余寿命预测的准确性和维修决策的科学性。针对传统寿命/退化试验方法存在的不足,能够快速经济地获取设备退化数据的加速退化试验得到了普遍关注,实现了广泛应用[1-2]。
机载设备常需要在高空、低压、低温、高振的环境下工作,运行环境的复杂多变性导致其退化的不确定性进一步加剧。由于Wiener随机过程在描述退化的时变不确定上具有天然优势,因此多被用于对机载设备进行退化建模。Wiener过程也称布朗运动过程,其在加速应力(温度)条件下将体现出更强的运动不确定性,因而现有研究多假设加速应力既影响Wiener过程的漂移系数又影响扩散系数,体现出对退化过程的综合影响。目前,基于上述假设的研究已围绕电缆、发光二极管(light emitting diode,LED)、加速度计等设备开展了实例分析,取得了一定成果[3-6]。例如,火箭军工程大学的唐圣金等人基于线性退化过程构建加速模型,并利用某型激光器的步进加速退化数据实现了对设备剩余寿命的预测,取得了良好效果[7]。然而,线性Wiener模型不具备普遍的适用性,导致该方法的应用受限。针对上述研究的不足,Hao[8]和Cai[9]等将非线性Wiener过程引入加速退化建模,并考虑了随机效应和测量误差对模型的不确定影响,从而建立了更具一般性的加速退化模型。然而,上述研究均认为加速应力仅与Wiener过程漂移系数存在函数关系,将扩散系数视为不随应力变化的常数,而未考虑到应力水平提升对退化不确定性增加的同步影响,从而在一定程度上影响了方法的准确性。针对上述方法存在的不足,Liu等[10]认为加速应力将同步影响漂移系数与扩散系数,并构建新的Wiener加速退化模型,有效提升了退化建模和剩余寿命预测的准确预测。然而,该方法将漂移系数与扩散系数视作独立变量分别建立加速模型,未能充分考虑漂移系数与扩散系数存在的关联关系,影响了预测精度的提升。为此,Wang等[11]采用特定共轭先验分布来描述漂移系数与扩散系数间的关联关系,并基于非线性Wiener过程建立了设备的加速退化模型。但该方法在建立退化模型的过程中,默认Wiener过程中的漂移/扩散系数服从类似正态-伽马分布的共轭先验分布,而当漂移系数与扩散系数不服从该分布类型时,此方法得到的剩余寿命预测结果缺乏可信性。进一步,考虑到加速退化试验需满足的加速因子不变准则,文献[12]提出了加速应力下漂移系数与扩散系数的比例关系假设,并据此构建加速退化模型,提升了剩余寿命预测方法的有效性。然而,该模型无法应用于加速应力场合,且未考虑个体差异和测量误差对退化建模的影响。
在上述剩余寿命预测研究中,均需要多个退化试验样本才能确保参数估计与剩余寿命预测的准确性。但在现实环境中,出于节约试验成本的考虑和产品研制进度的制约,在研制阶段参与加速退化试验的机载设备样本数量往往很少,甚至可能只有一个。这种立足于单一设备状态检测数据实时推导剩余寿命概率分布的方法称为设备剩余寿命的自适应预测方法,目前国内外关于此内容的研究不多。孙国玺等[13]将设备的退化过程刻画为一种基于随机系数的非线性回归模性,并在贝叶斯框架下利用期望最大化(expectation maximization, EM)算法实现了对设备剩余寿命的自适应估计。然而,该方法假设设备的非线性回归过程满足指数过程,具备严格的单调性。难以准确反映非单调退化设备的真实退化特性,降低了模型的适用性,影响了剩余寿命预测的准确性。考虑到设备退化存在的单调/非单调可能,司小胜等[14]将Wiener过程引入传统剩余寿命自适应预测研究,提出综合运用EM算法和卡尔曼滤波(Kalman filter, KF)方法来实时估计设备的真实退化状态和在线更新退化模型参数。并通过单个陀螺仪的实测退化数据,对所提方法进行了验证。在司小胜等[14]研究的基础上,Feng等[15]将其拓展至非线性场景,提出了基于EM和扩展KF(extended KF, EKF)的剩余寿命自适应预测方法,并就锂电池的性能退化数据开展了分析。然而,司小胜等[14]和Feng等[15]的研究均未考虑个体差异对设备剩余寿命预测的影响,也无法在加速应力环境下进行应用。
针对现有研究存在的不足,本文综合考虑单一加速退化试验样本和漂移系数与扩散系数的比例关系对机载设备剩余寿命预测的影响,开展了单台机载设备加速退化试验条件下的退化模型构建与剩余寿命预测研究。首先,基于加速因子不变准则建立了设备的比例加速退化模型,并同步考虑了测量误差与个体差异;其次,基于KF原理在线更新设备的退化状态;然后,针对加速退化试验仅有单一样本的情形,提出基于EM-KF算法的参数自适应估计方法;最后,基于全概率公式推导出剩余寿命的概率密度函数。通过对单台行波管加速退化试验的实测数据进行分析,验证了方法的合理性和有效性。
1 比例加速退化模型
基于Wiener过程的一般退化模型如下所示:
X(t)=X(0)+αt+βB(t)
(1)
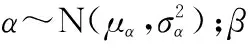
由式(1)易知,其退化过程为线性过程。而在真实环境下,设备退化过程对线性/非线性兼而有之,因此更具一般性的非线性退化模型具有普遍的适用性,其具体表达式为
X(t)=X(0)+αφ(t|θ)+βB(φ(t|θ))
(2)
式(2)也被称为时间尺度变换模型。其中,φ(t|θ)表示时间t的非线性函数,θ表示未知参量。
文献[16]证明了加速因子不变准则,即在加速试验有效的前提下,加速应力将同步影响退化模型的漂移系数和扩散系数,且影响程度同漂移系数或扩散系数的平方成正比,由此可得
(3)
式中:S1与S2分别表示加速应力;AS1,S2是一个仅与应力大小有关的参数;αS1,αS2,βS1,βS2则分别对应不同加速应力条件下的漂移系数与扩散系数。
则由式(3)易得
(4)
式中:ρ为比例系数。由于加速应力S1与S2具有任意性,则对于式(2)所示退化过程,可知式(4)恒成立。
设备加速模型的一般形式可表示为
α=g(S|κ)
(5)
其中,κ为未知参量。
则将式(4)与式(5)带入式(2)即可得到比例加速退化模型:
(6)
考虑到状态监测过程中由于测量方法、环境影响等对设备退化状态获取产生的不确定性影响,本文将测量误差引入比例加速退化模型,可得
(7)
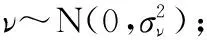
2 基于KF的退化状态在线更新
为便于分析,本文基于指数加速加速模型进行分析,其他加速模型分析过程与该模型相同,在此不再加以赘述。指数加速模型的一般表达式为
g(S|κ)=aexp(bS)
(8)
式中:κ=[a,b];S为电应力。

(9)
接下来,本文基于KF原理对设备的退化状态进行在线更新。假设ti|Sj为目标设备的第i个监测时刻,且其对应的加速应力为Sj,则Yi=Y(ti|Sj)与Xi=X(ti|Sj)分别为对应时刻设备性能退化量监测值和真实值;而Y1:k=[Y1,Y2,…,Yk]则表示直至tk时刻已获取的全部退化数据。
联立式(7)与式(8)可得比例加速退化模型的状态转移方程,具体可表示为
(10)
式中:Δφ(tk|θ)=φ(tk|θ)-φ(tk-1|θ),t0=0;且易知B(Δφ(tk|θ))=B(φ(tk|θ))-B(φ(tk-1|θ))。
由于式(10)中存在非线性函数Δφ(tk|θ),导致传统KF方法无法应用。针对此类情形,通常需要采用诸如文献[15]中提出的EKF方法来对退化模型的状态进行更新。但该方法需要利用幂级数展开的方式来实现对非线性函数的线性化处理,从而极大增加了迭代的复杂性,且其产生的高阶无穷小项也会引起不确定误差。为了解决上述问题,本文采用一种直接的线性化方法来对式(10)进行处理,从而有效简化了KF迭代的过程,提升了状态估计的准确性。
不妨令:
(11)
(12)
(13)
L=[1,0]
(14)
由此可得
(15)

(16)
(17)
(18)
(19)
基于上述分析,可给出KF的具体更新过程为
(20)
Pk|k=Pk|k-1-KkLPk|k-1
(21)
(22)
(23)
(24)
其中,
3 基于EM-KF的参数自适应估计
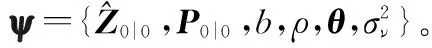
进一步,基于式(15)给出的设备状态方程,可得
L(ψ)=lnP(Z0:k,Y1:k|ψ)=
lnP(Z0:k|Y1:k,ψ)+lnP(Y1:k|ψ)=
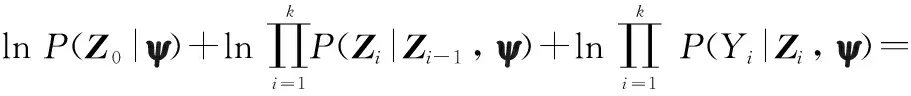
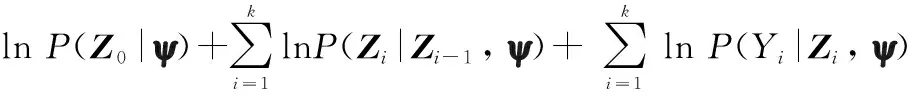
(25)
式中:Y1:k为实时监测得到的设备退化数据;P(Z0:k,Y1:k|ψ)为Y1:k与Z0:k在给定退化参数ψ条件下的联合概率密度。
基于本文假设,易知:
(26)
Zi|Zi-1,ψ~N(AiZi-1,Qi)
(27)
(28)
(29)
进一步,将上述结果代入式(25),可得:
L(ψ)=lnP(Z0:k,Y1:k|ψ)∝
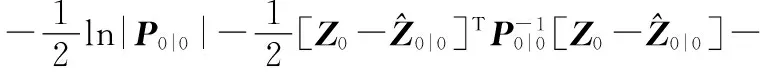


(30)

步骤 1对式(30)求解关于Z的期望值,也称E步。



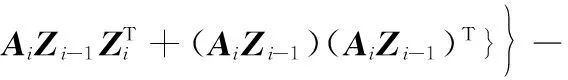
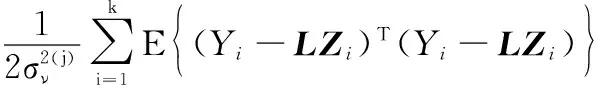
(31)
步骤 2求式(31)对应的极大值,也称M步。
式(31)包含未知参数多,且其估计结果随设备退化状态更新结果的变化而变化,因此无法通过解析法直接进行求解。为此,本文利用文献[17]中提出的RTS(rauch tung striebel)后向平滑滤波器来对其进行估计。其具体求解过程如下:
(32)
(33)
(34)
(35)

(36)
(37)
(38)
利用RTS基本原理可得
(39)
基于上述分析,可将式(31)转为
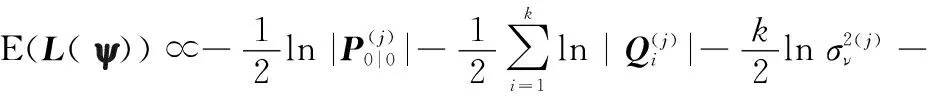

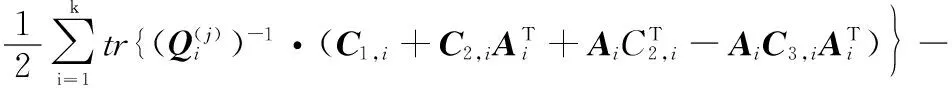
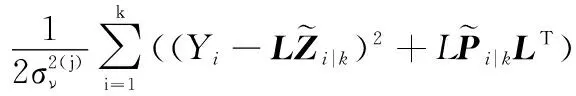
(40)
其中:
(41)
(42)
(43)

(44)
(45)
(46)
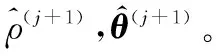
4 设备剩余寿命自适应预测
设备的寿命T通常被定义为其性能退化量首次超过预设失效阈值D的时间,对应的数学表达式为
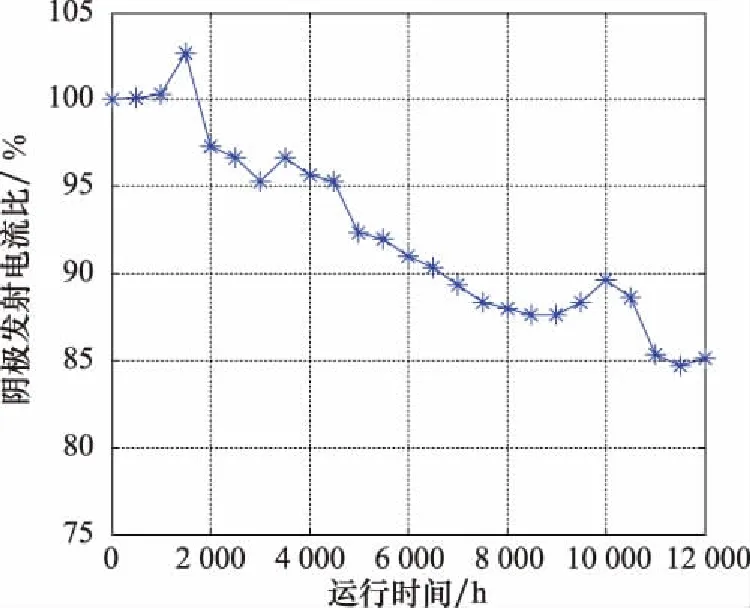
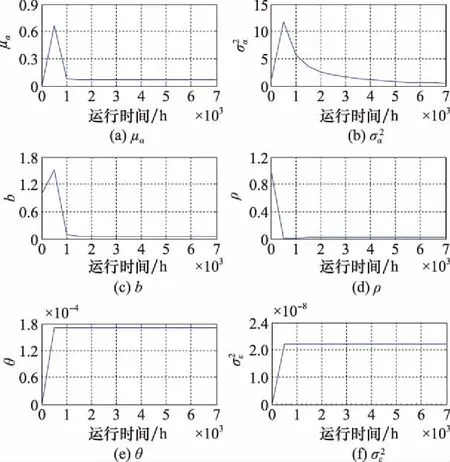
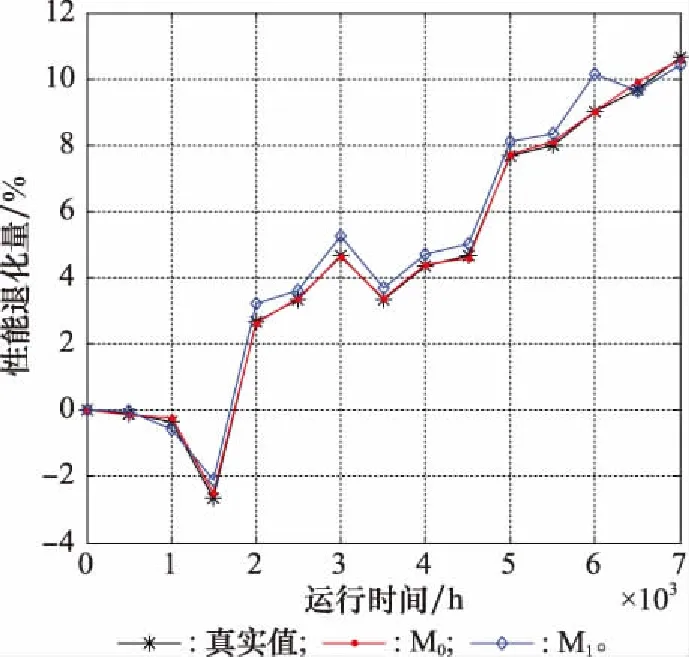
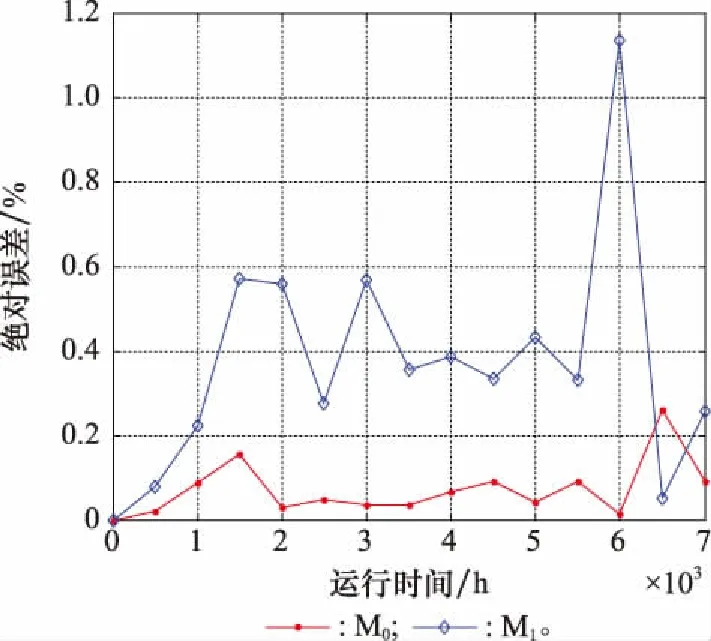
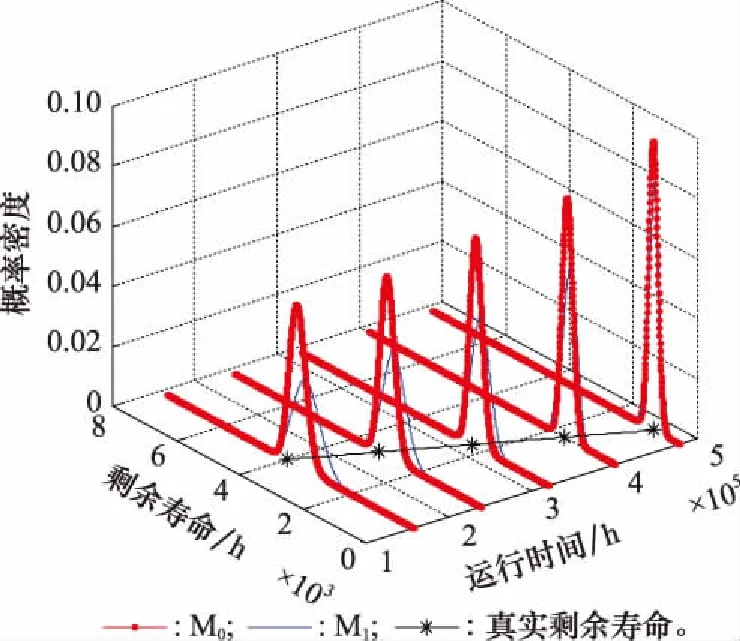
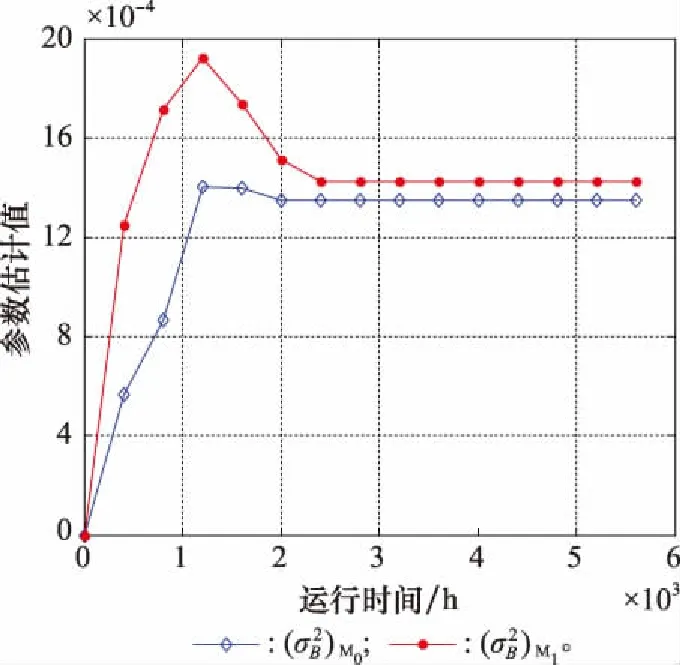
T=inf{t:X(t)≥D|X(0) (47) 若设备退化过程如式(2)所示,则其寿命的概率密度函数可表示为[18] (48) 设备的剩余寿命一般是指从当前时刻tk运行至设备失效的时间间隔,参照设备寿命的定义式,易于给出剩余寿命的定义式为 L=inf{lk:X(tk+lk)≥D|X(0) (49) (50) (51) 对应设备寿命的概率密度函数式(48),将失效阈值D变更为D-xk,将寿命的非线性函数φ(t|θ)变更为剩余寿命的非线性函数ψ(lk),进而可得基于时间尺度模型的剩余寿命概率密度函数为 (52) 若给定ak,Xk,Sj,并将加速退化模型式(8)与比例关系模型式(4)代入式(52),即可得到式(7)所示非线性比例加速退化模型的剩余寿命条件概率密度函数为 (53) 由二维正态分布性质可知,ak与Xk分别满足如下条件概率分布: ak|Y1:k~N(E(ak|Y1:k),D(ak|Y1:k)) (54) Xk|ak,Y1:k~ (55) 基于全概率公式,即可实现对目标设备剩余寿命的自适应预测,且对应的剩余寿命概率密度函数与累积分布函数分别为 P(Xk|ak,Y1:k)·P(ak|Y1:k)dXkdak (56) (57) 行波管是机载导航、雷达、电子对抗系统的核心部件,具备高可靠性、高价值、长寿命的特点。本文基于某型行波管单台加速退化试验数据进行分析,如图1所示,具体试验条要求如下: 图1 行波管加速退化数据 (1)行波管的性能退化量选用阴极发射电流; (2)行波管以加速应力8 A/cm2(加速应力为电流密度,且其正常工作应力约为1 A/cm2)进行恒定应力加速退化试验; (3)当行波管的阴极发射电流下降至初始时刻的10%时可认为该行波管发生失效(对应的真实寿命为7 000 h)。 由图1可以发现,行波管的退化路径具有明显的非线性特征,且对该行波管性能退化增量进行K-S假设检验后不能拒绝其服从正态分布的假设,从而表明采用非线性Wiener过程对该行波管进行建模分析具有合理性。 图2 参数自适应估计过程 为便于分析,记本文所提方法为M0;与之相对应,将忽略漂移/扩散系数比例关系的退化模型所对应剩余寿命自适应预测方法记为M1。结合前文得到的退化模型参数自适应估计结果,基于KF原理即可对设备的退化状态进行在线更新,具体更新结果如图3所示。 图3 退化状态在线更新 图3中设备退化量的真实值,是将图1中初始时刻退化量设定为0后得到的。由图3可知,M0对应设备退化状态的预测值较M1与真实退化量更为接近,表明考虑漂移系数与扩散系数比例关系的退化模型更能反映设备的真实退化规律,具备更好的模型拟合性。为了更为直观地讨论M0与M1的差异,本文给出不同方法对应退化状态预测结果的绝对误差,具体如图4所示。 图4 退化状态预测误差 由图4可知,M0的退化状态预测误差要显著小于M1。究其原因,主要是由于M1忽略了漂移系数与扩散系数的比例关系,从而导致该方法对设备退化状态进行估计的不确定性增大,进而产生了较大的误差。因此,有必要在退化建模过程中考虑漂移系数与扩散系数的比例关系。 在第5.1节与第5.2节分析的基础上,基于本文提出的剩余寿命自适应预测方法,即可对设备的剩余寿命进行预测。一般情况下,该型行波管的正常工作应力S0约为1 A/cm2,其对应的剩余寿命预测曲线如图5所示。 图5 剩余寿命预测结果 由图5可得,本文方法和对照方法均可准确预测设备的剩余寿命,其直观体现为两种方法对应的剩余寿命概率密度函数在任意状态监测时刻均可完全包含设备的真实剩余寿命。然而,进一步分析可以发现,本文方法对应的剩余寿命预测曲线较对比方法的聚集程度更高,说明本文方法的不确定性更低,预测精度更优。进一步,令: 图6 扩散系数更新情况对比 由图6可知,在扩散系数更新的全过程中,M0对应的扩散系数较M1更小,表明利用比例关系模型可以更为准确地描述退化的时变不确定性,有效降低预测的不确定性,从而显著提升剩余寿命预测方法的性能。该结论也进一步验证了第5.2节中的结论。 本文针对单一机载设备在加速退化试验条件下的退化建模和剩余寿命预测问题进行了研究,具体结论如下。 (1)利用加速因子不变准则推导出漂移系数与扩散系数间的比例关系,并据此构建了加速应力环境下的设备退化模型。拓展了模型的适用性,提升了建模的准确性,实现了对设备剩余寿命的准确预测。 (2)针对加速退化试验仅有单一样本的情形,提出基于EM-KF算法的参数自适应估计方法,克服了传统参数估计方法需要大量试验样本的局限性,实现了对模型参数的准确估计。


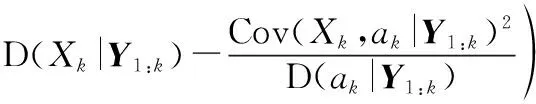

5 实例分析
5.1 参数自适应估计

5.2 退化状在线更新
5.3 剩余寿命自适应预测
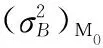
6 结 论
