多无人机协同探测快速目标的控制方法设计
2021-11-10符小卫陈子浩
符小卫, 陈子浩
(1.西北工业大学电子信息学院, 陕西 西安 710129;2.湖北航天技术研究院总体设计所, 湖北 武汉 430040)
0 引 言
无人机因为其独特的优势被充分运用于各种作战任务,典型的任务场景有:目标围捕[1-3]、目标追踪[4-6]、协同目标探测打击[7-9]等,研究这类问题可以极大的提升无人机作战智能化程度。其中协同目标探测问题[10-11]主要研究如何控制无人机编队自主协调的利用队形去侦察探测个体或群体目标,在军事领域具有重要的研究价值,因此很多专家投入到相关的研究中。
文献[12]基于光电载荷提出了一种无人机编队协同定位、跟踪地面目标的算法。文献[13]建立了基于多Agent的无人机群区域探测协同作战模型,利用战场信息作出较为准确的判断,从而选择探测路线。文献[14]为了提高定位精度,提出了一种保证通信距离约束和传感器探测距离约束性能的无人机双机协同探测路径规划算法。文献[15]将多智能体技术和信息融合技术引入无人机编队系统中,构建出无人机编队协同探测任务规划体系和编队协同探测信息融合体系,进而探讨了基于多智能体技术的无人机编队协同探测策略。文献[16]提出了一种无人机协同探测目标问题的控制算法,能够有效合理地完成分布式协同探测任务。文献[17]针对单个飞机接近支援干扰问题,提出了一种双机协同支援干扰模型,有效提升了支援性干扰压制力不足的问题。文献[18]主要探究了多架无人机从不同机场起飞执行协同探测的问题,以减少被敌方雷达发现时间为目的,将最小停留时间问题转化为最短路径组合优化问题,利用遗传算法对模型进行求解,生成具有价值的侦察路径。文献[19]研究了多无人机系统中多目标跟踪探测的协同决策问题,基于一致联合多目标概率分布,采用分布式可观测马尔可夫决策算法进行跟踪决策。文献[20-21]基于一致性的方法,对无人机编队的控制方法进行了分析,提出了一种有限控制一致性协议,在不预先对多智能体网络进行分组的情况下,可以实现多个无人机编队的控制,并运用到对目标的协同探测和围捕中。
现有的文献从多种角度研究设计了无人机协同探测方法,但仍然存在一些问题。首先,大部分文献研究的是多无人机协同探测的概率问题和任务分配问题,对无人机编队的控制问题讨论较少。其次,传统无人机载荷控制还需要人工操作进行跟踪探测,如果可以解决载荷的角度控制、编队无人机姿态自平衡等关键技术环节,携带侦察载荷的无人机编队就可以具备编队一边行进、一边所携带载荷探测扫描的能力,这将加强无人机编队的智能化程度。而且,无人机协同探测任务中所设定的目标性能一般弱于无人机,当目标的速度大于无人机的速度时,现有的方法可能无法作出良好的应对。因此,针对快速运动目标,本文从无人机载荷角度控制和无人机编队控制的方向,提出了快速目标的多无人机协同探测方法。
本文首先引入了固定时间控制一致性协议到无人机载荷角度控制中,控制载荷持续照射目标;然后引入有限时间一致性协议到无人机编队控制中,用以形成协同探测队形,并通过二跳网络加快队形的收敛。根据载荷特性设计了针对快速运动目标的无人机协同探测队形,通过将无人机队形控制与无人机载荷的角度控制相结合,实现了无人机编队对快速目标的协同探测。
1 多无人机系统模型
1.1 无人机运动模型
假设二维空间中有n个无人机编队飞行,并按照1,2,…,n的顺序对其编号,并且系统中所有无人机都是相同的机械结构构型,因此用下式来描述系统中的无人机模型:
(1)
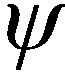
(2)
式中:ri,vi,ui∈Rm(m=2;i=1,2,…,n);ri表示第i架无人机在惯性坐标系中的二维坐标;vi表示第i架无人机的速度。
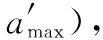
(3)
(4)
1.2 通信网络拓扑结构
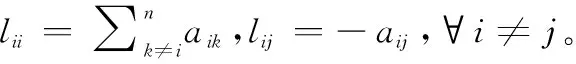
(5)
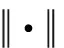
2 多无人机协同探测控制
2.1 无人机载荷模型
编队中的每架无人机都携带相同类型的载荷,该无人机载荷在平面上可360°旋转,其探测范围为扇形,图1中由点U、A、C、B围成,称其为探测器的“探测靶面”,简称为“靶面”。当存在目标于靶面内时,无人机即可发现该目标,无人机所携带的载荷模型如图1所示,其中蓝色圆球表示被探测目标。探测半径为R,即UA=UB=R,∠AUB表示探测器的水平视场角, ∠AUB=2ζ,靶面范围位于扇形中线的[-ζ,ζ]区域。无人机载荷的任务是尽可能地使用靶面去照射目标,从而完成探测任务。
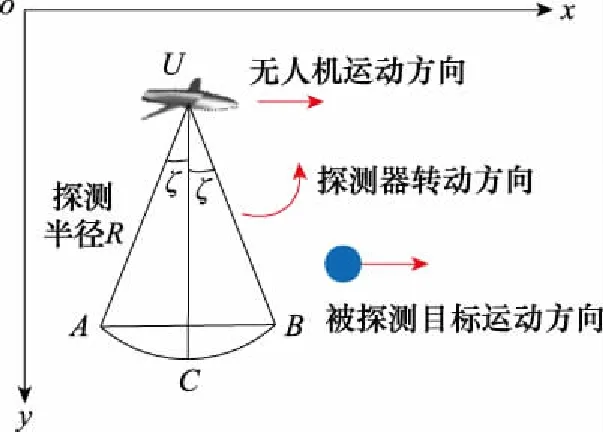
图1 无人机载荷模型
2.2 无人机载荷角度控制律
本文中假定目标的运动速度比无人机要快,如果无人机携带固定角度的载荷去探测快速运动目标,那么会因为两者的速度差过大从而造成探测时间过短,从而无法达到任务要求。为解决该问题,本文中引入载荷角度控制,通过一致性算法实现载荷对目标的持续跟踪,从而尽可能的延长目标被探测时间。
引理 1[22]连通无向图G具有n个节点,其Laplacian矩阵L有如下性质:
(1)矩阵L是半正定矩阵;
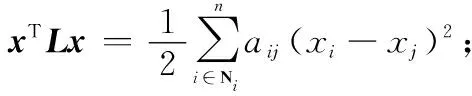
(3)如果矩阵L的特征值为{0,λ2,…,λn}并满足0≤λ2≤…≤λn的条件,则矩阵L第二小的特征值λ2>0;若满足1Tx=0,则xTLx≥λ2xTx。
引理 2[23]假定m1,m2,…,mn≥0,0
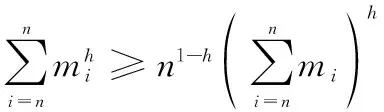
引理 3[24]若函数V(x(t)):Rn→R+∪{0}是连续径向有界,如果该函数满足:
(1)V(x(t))=0⟺x=0;
(2)对于任意x(t)都可满足:
(6)
其中,α、β、p、q、k为正参数,并满足pk<1、qk>1。
那么整个系统可在固定时间内完成收敛,最终达到一致性,并且整个过程的收敛时间Ts满足:
(7)
假设无人机编队中有n个无人机,无人机各自携带载荷,载荷模型如图1所示。每个无人机所携带的载荷转向运动学模型采用一阶积分模型:
(8)
式中:ϑi表示第i架无人机靶面中线与x轴所成角度,称为载荷视场角;ωi表示第i架无人机载荷的旋转角速度。
由于目标运动速度较快,留给无人机载荷的探测时间有限,为了在有限的时间内实现载荷的协同跟踪,引入了固定时间一致性算法[9],使得载荷的角度在固定时间内收敛至期望角度,从而提高任务完成效率,通过该算法设计了基于角度信息的无人机载荷角度控制律:
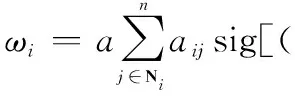
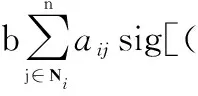
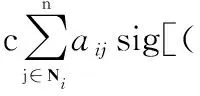
(9)
式中:a、b、c为角度控制增益;s∈(0,1);t∈(1,∞);aij表示无人机编队的通信网络结构,无人机载荷的角度信息也可随通信网络流通;Δi表示期望角度偏差,利用Δi实现对期望角度的收敛,sig函数为
sig(x)z=|x|zsign(x)
(10)
其中,sign为符号函数,其具体含义为
(11)
通过控制律式(9)的设计,可以将系统的收敛时间Ts计算得出,而根据引理3可以发现,系统的最大收敛时间Tmax由α、β、p、q、k这些参数计算得出,但这些参数只与控制律参数设计、编队中无人机的架数和Laplacian矩阵的第二小特征值λ2相关,无人机载荷的初始状态与其无关。
定理 1假设无人机编队的通信网络结构为无向图,即该系统的Laplacian矩阵L是半正定矩阵,则无人机的载荷系统利用控制律(9)可以在固定时间内收敛至一致,并且收敛时间Ts满足:
(12)
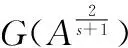
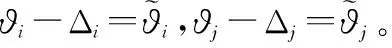
(13)
对式(13)求一阶导数,可得
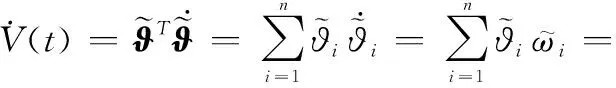
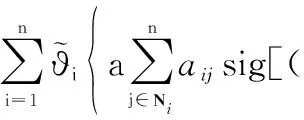
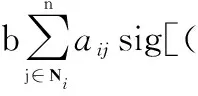
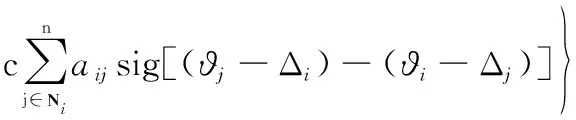
(14)
由引理1可将式(14)转换为
(15)
由引理2可知,式(15)满足:
(16)
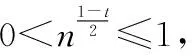
(17)
结合式(16)和式(17),可得
(18)
根据引理1可得
(19)
所以:
(20)
综上所述,无人机编队的通信网络结构只需要为无向图,即该系统的Laplacian矩阵L是半正定矩阵,即可满足式(20)。所以无人机的载荷系统利用控制律式(9)可以在固定时间内收敛至一致,并且收敛时间Ts满足式(12)。
证毕
在控制律式(9)的控制下,无人机载荷最终是否成功跟踪探测目标的判定标准为
(21)
期望角度偏差Δi的计算类同于队形偏差,此时将目标选取为参考中心点,如图2所示,蓝色圆形表示快速运动目标。期望角度偏差Δi为无人机和目标之间的连线与水平轴线所成的角度,如1号无人机的期望角度偏差Δi为∠TAI,各个期望角度偏差组合起来成为期望角度偏差矩阵Δ,图2中有4架无人机携带探测载荷组成编队,那么该编队的期望角度偏差矩阵Δ为Δ=[∠TAI, ∠TBI, ∠TCI, ∠TDI]。
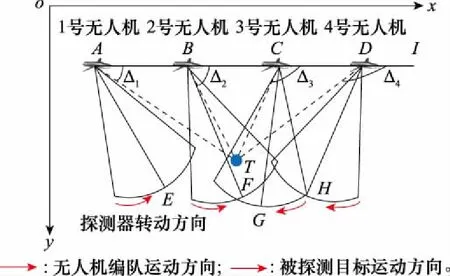
图2 期望角度偏差的计算
2.3 无人机协同编队探测控制律
定义1[25]对于系统
(22)
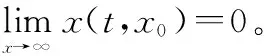
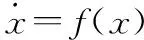
引理 4[27]对于系统式(22),如果满足系统全局渐近稳定和具有负齐次度的条件,则该系统是全局有限时间稳定。
引理 5[28]假设函数满足f(xi,xj)=-f(xj,xi),i≠j的条件,则集合(y1,y2,…,yn)满足:
(23)
假设无人机编队中有n个无人机去执行协同编队探测任务,已通过固定时间一致性的算法对无人机所携带的载荷进行控制,为了达到更好的探测效果,需要设计合适的无人机编队控制协议以及更高效的编队队形去配合载荷,从而尽量延长目标被探测的时间,为此引入有限时间一致性算法,以此来实现无人机编队协同探测队形的收敛,并且考虑二跳网络的情况,使得收敛速度加快。
由于无人机载荷角度控制的限制,考虑无人机编队的通信网络结构为无向连通图。根据有限时间一致性算法,设计第i架无人机的控制律为
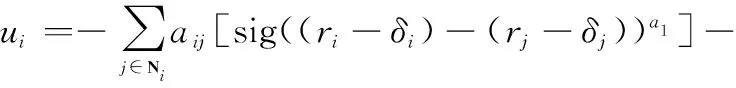
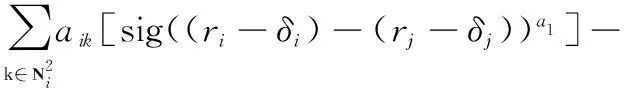
sig(ri-δi-rd)a1-sig(vi-vd)a2
(24)
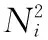
(25)
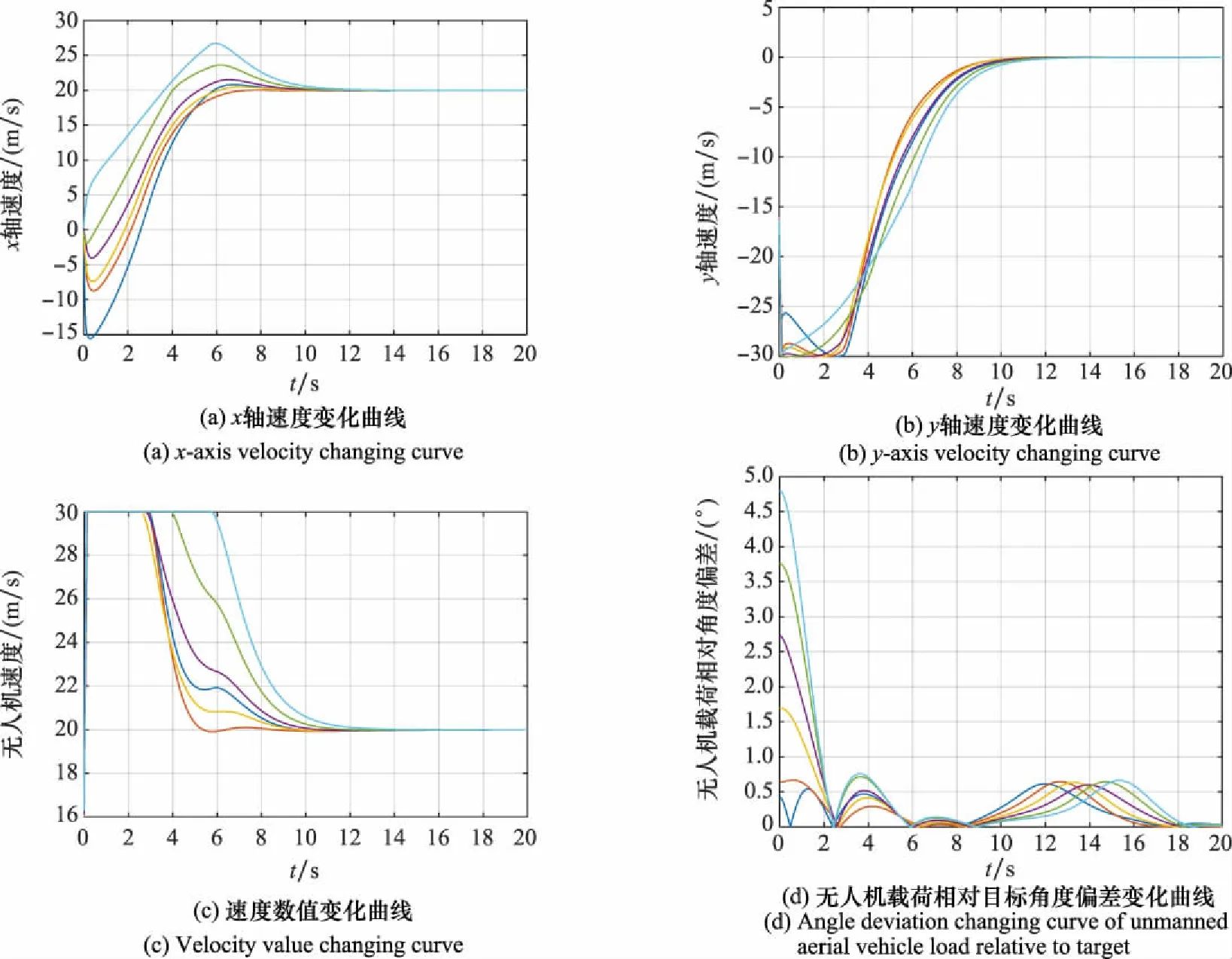
定理 2假设无人机编队的通信网络结构图是无向连通图,并且无人机编队期望状态的信息全局可达,则在确保0 证明根据引理4,需要证明系统的全局渐近稳定性和负齐次度,才能得到该系统是全局有限时间稳定,因此将证明分为两个部分。 (1)全局渐近稳定性证明 (26) 对于无人机编队系统,选取Lyapunov函数如下: (27) 整个系统的Lyapunov函数为V(t)=V1(t)+V2(t)+V3(t)+V4(t)。对式(27)分别求导得 (28) 由式(28)可得 (29) 结合引理5,将式(29)展开化简得 (30) (31) 也就代表着 (32) (2)负齐次度证明 定义ξ1=2-a2,ξ2=1,对于某f>0,将无人机编队系统转换为 (33) 将a1=a2/(2-a2)代入式(33),可得 (34) 结合式(33)和式(34),可得 (35) 根据定义2,可得无人机编队系统的齐次度k=a2-1。 因为0 综上所述,根据引理4,当无人机编队系统具有全局渐近稳定性和负齐次度时,无人机编队可在有限时间内稳定,从而定理2得证。 证毕 本节主要对无人机协同探测控制律式(24)及无人机载荷角度控制律式(9)的有效性进行验证,参数设置如表1~表2所示。仿真实验在二维空间下,快速运动目标的运动方式设计为匀速直线运动,为了尽可能地延长目标被探测时间,将无人机编队协同探测队形设计为一字型,在这种队形设计下,无人机载荷的探测区域会更长,从而获得更长的探测时间。 表1 无人机载荷角度控制律式(9)参数设置 表2 无人机协同探测控制律式(24) 无人机之间的通信网络结构如图3所示,图3(a)显示的是根据队形位置结构, 图3(b)显示的是无人机编队通信网络结构,其中给出了各无人机之间的通信关系,设定无人机编队的通信网络图中的每条边的权重为1,无人机载荷的探测半径为100 m。仿真时长T设置为15 s。6架无人机的初始位置、初始速度的值如表3所示。目标初始位置为(-300,200)m,初始速度为(50,0)m/s。 图3 无人机编队队形设计与通信网络结构 表3 无人机编队初始状态 在图3下无人机编队的邻接矩阵、Laplacian矩阵、入度矩阵分别为 根据式(9),结合表1中参数设置,可计算出无人机载荷角度的固定一致时间为3.97 s。初始状态下,由于目标位置未知,为了增大探测到目标的概率,将无人机编队设计成六边形,各架无人机载荷所成角度环绕360°,并都按照(0,-15)m/s的速度朝目标可能来袭方向运动。在无人机协同探测控制律式(24)下,无人机编队的位置及形成的协同探测队形如图4所示,在无人机载荷角度控制律式(9)下,无人机编队的载荷角度旋转情况如图4所示,图中蓝色五角星表示无人机当前所在位置,扇形区域表示无人机载荷的探测区域,无人机前的箭头表示无人机当前的速度方向,无人机尾后线条表示无人机运动后的轨迹,图上数字表示仿真时长,黑色圆圈表示快速目标,亮绿色线条表示目标运动轨迹。 图4 无人机编队协同探测仿真 无人机编队速度、无人机编队相对位置偏差、无人机载荷相对目标角度偏差、目标被发现情况如图5所示。图5(a)~图5(b)显示的是仿真过程编队中各架无人机在各个坐标轴上的速度变化曲线,图5(c)显示的是无人机编队速度数值的变化曲线,可以观察到无人机编队最终收敛至速度vd=(20,0)m/s,收敛时间为12 s左右。图5(d)显示的是无人机编队相对目标角度偏差的变化曲线图,图5(e)显示的是无人机编队相对位置偏差的变化曲线,图5(f)显示的是目标在整个仿真过程中被发现的时间区间。由于目标在不断的运动,所以图5(d)显示的无人机载荷相对角度一直处于收敛之中,当相对角度为0时,表明目标处于探测范围内的中线位置。图5(f)显示的是目标被载荷发现的时间段,由此可得目标整个过程中被发现时间为8.1 s。从而证明了无人机协同编队探测控制律及无人机载荷角度控制律的有效性。 图5 无人机编队的收敛指标 本文针对快速运动目标,设计了载荷和队形相互配合的控制律。由于目标的性能参数比无人机要强,为了完成协同探测任务,通过无人机载荷建模,将无人机编队控制和载荷角度控制相结合,引入了固定时间控制一致性协议到角度控制中,实现无人机对高速运动目标探测时间的最大化;与此同时基于有限时间控制一致性协议,完成无人机协同探测队形的设计及收敛,实现了队形收敛与载荷控制的相结合,从而极大地延长了高速运动目标被发现的时间。最后通过仿真实验和数学分析证明了以上算法的有效性。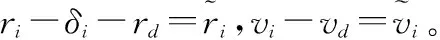
3 仿真分析


4 结 论
