基于细菌觅食算法的多异构无人机任务规划
2021-11-10谷旭平唐大全
谷旭平, 唐大全
(海军航空大学航空作战勤务学院, 山东 烟台 264001)
0 引 言
随着无人机(unmanned aerial vehicle,UAV)军用和民用价值日益显著。UAV遍及地形勘测[1-2]、电力巡检[3]、军事行动[4-5]、环境监测和灾难响应[6-7]、智能农业[8-9]、商业运输[10-11]等行业。随着作战任务日益繁琐以及作战环境的复杂多变,单UAV已经不能满足日益复杂的任务需求,因而集群作战成为主流。任务规划对释放UAV潜力提高集群性能起着关键作用。
任务规划包括任务分配与航迹规划两方面。任务分配的求解包括任务分配模型和算法,任务分配模型分为集中式和分布式。集中式包括:多旅行商问题模型[12]、通用分配问题模型[13]、车辆路径问题模型[14]、混合整数线性规划模型[15]、多UAV协同任务分配模型[16]、随机博弈论任务分配模型[17]等。集中式算法包括:蚁群算法[18]、粒子群算法[19]、遗传算法[20]、捆绑算法[21]等。分布式任务分配模型主要为合同网协议模型,相应算法为智能拍卖算法[22]。集中式特点在于全局性强,对于强耦合的任务分配具有优势,但计算量大、鲁棒性差、实时性不高。分布式的特点在于环境适应度好、计算量小、鲁棒性高,但全局性差,适合于实时性要求高、动态特性强的任务环境。
航迹规划算法包括群体智能算法[23]、人工势场法[24]、基于几何学的路径规划算法[25]、基于控制理论的路径规划算法等。势场法是通过建立作战区域的势场环境,UAV在势场导向中完成航迹规划。
本文针对多UAV任务规划问题,综合考虑航迹规划对整个编队任务分配的影响,一方面融合Lyapunov导航向量场以及避障向量场,在动态和静态障碍干扰下,寻求最优可飞航迹;另一方面,改进细菌觅食算法,寻求最优任务分配结果;在任务分配过程中,基于合同网拍卖算法,进行UAV故障环境中的任务重分配。
1 模型建立
1.1 模型描述
定义由D架强击机、E架侦察机、F架轰炸机构成的UAV集群:U={U1,…,UD,UD+1,…,UD+E,UD+E+1…,UN},N=D+E+F,其中前D架为强击机,中间E架为侦察机,后F架为轰炸机。定义M个作战目标集合:AIM={A1,A2,…,AM},每个作战目标都需进行侦察(Classify, C)、攻击(attack, A)、评估(verify, V)任务,任务集合T={T1,T2,…,TG},G=3×M。UAV依据其功能,执行相应任务,具体情况为:①强击机C、A、V;②侦察机C和V;③轰炸机A。
1.2 约束条件
(1)任务数量约束
(1)
(2)
(2)任务执行情况约束
(3)
(3)任务时序约束
(4)
式(4)表示目标Ai的任务执行次序为侦察、攻击、评估。
(4)机载弹药约束
(5)

1.3 任务分配评价指标
(1)UAV完成任务付出代价:
C1=UAVVALUE·(1-TASKTHI)
(6)
式中:UAVVALUE∈[0,1]为UAV的价值;TASKTHI∈[0,1]为目标威胁系数。
(2)UAV航程代价
(7)
式中:dmax为UAV执行任务的最远距离; Dist(Tij)为UAV执行任务Tj的航程。
(3)UAV攻击收益
(8)
式中:TASKVALUE∈[0,1]为目标价值。
(4)总体收益
(9)

2 细菌觅食算法
2.1 细菌觅食算法
细菌觅食算法[26](bacterial foraging optimization, BFO)依据细菌的趋向、繁殖和迁徙行为,实现种群优化。为方便描述引入符号:S为种群大小,Nc为趋向操作次数,Ns为趋向操作在任一方向上游动的最大步数,Nre为繁殖行为次数,Ne为迁徙行为次数,Ped为迁徙概率。
2.1.1 趋向操作
趋向方式:细菌任选一方向游动,若适应度增加,则继续朝该方向游动,直到达到最大步数Ns,否则转换方向游动,直到达到趋向次数Nc。细菌i的趋向操作表示为
(10)
式中:Δ表示随机方向上的单位向量;C(i)为游动步长;θi(j,k,l)表示细菌i在第j次趋向操作、第k次复制操作、第l次迁徙操作后的位置。
2.1.2 繁殖操作
繁殖方式:依据式(11)衡量细菌趋向后的适应度,并进行排序,淘汰掉Sr=S/2个能量较小的细菌,复制剩余Sr个细菌。
(11)
式中:J(i,j,k,l)表示细菌i在第j次趋向操作、第k次复制操作、第l次迁徙操作之后的适应度。
2.1.3 迁徙操作
细菌以给定概率Ped进行迁徙操作,即若细菌i满足迁徙概率,则随机分布到寻优空间中。
2.2 BFO的改进措施
2.2.1 趋向操作的改进
为提高算法前期的全局收敛能力,C(i)应较大,为增强后期局部收敛能力,C(i)应较小。改进的趋向操作如下。
步骤 1依据式(12)进行细菌灵敏度赋值,可表示为
(12)
式中:V是灵敏度;J为适应度;rand为随机数。
步骤 2翻转,产生随机向量Δ(i),依据式(10)进行方向调整。
步骤 3游动,若适应度得到改善,则按翻转方向游动,直到适应度不变,游动步长变为
C(i)=C(i)V
(13)
步骤 4按照式(14)线性递减灵敏度
(14)
2.2.2 繁殖操作的改进
为提高算法前期收敛速度,繁殖数要大;为避免中期陷入局部极值,繁殖数要小;为提高后期全局收敛能力,繁殖数要大。自适应繁殖数为
(15)
式中:k为繁殖算子当前迭代数;q为迁徙算子当前迭代数。
2.2.3 迁徙操作的改进
对全局最优附近的细菌而言,迁徙为解的退化。采用遗传算法的轮盘赌局作为选择机制,适应度较小的细菌迁徙,适应度较大的细菌迁徙概率小。自适应迁徙概率为
(16)
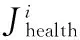
2.3 改进细菌觅食算法流程
改进精度的细菌觅食算法(IBFO-1)流程:
步骤 1初始化参数S,Nc,Ns,Nre,Ned,Ped,定义算法迭代次数为iter,i=0;
步骤 2若i 步骤 3判断是否达到迁徙次数Ned,达到则i=i+1,并返回步骤2,否则进行一次迁徙操作并进入步骤4; 步骤 4判断是否达到繁殖次数Nre,达到则返回步骤3,否则进行一次繁殖操作并进入步骤5; 步骤 5进行Nc次趋向操作,并返回步骤4。 BFO易跳出局部极值,但为一个3层循环,且所需要参数较多,不利于解决大规模问题。故采用改进实时性的细菌觅食算法(IBFO-2),按照繁殖、迁徙、趋向进行细菌觅食,并循环迭代。 任务规划通常将任务分配和航迹规划分开研究,本文通过建立UAV动力学模型,在Lyapunov融合向量场[27-29]中,将UAV的真实航迹转化具体航程信息融入到任务分配收益函数中,将任务分配与航迹规划融合到一起。 UAV的动力学方程为 (17) 式中:(x,y)T为UAV坐标;u1为UAV航速;θ∈[0,2π)为航向角;u2为UAV转弯控制输入量。 若UAV横坐标集合为X={x1,x2,…,xn},纵坐标集合Y={y1,y2,…,yn},则UAV的航程可以为 (18) 3.2.1 基于Lyapunov的导航向量场 导航向量场保证UAV以一定距离进行目标的侦查、攻击和评估。假定UAV最小观测距离为Rs,目标位于(xA,yA),UAV位于(xU,yU),则以(xA,yA)为中心的Lyapunov函数为 (19) 式中:R2=(xA-xU)2+(yA-yU)2为UAV与目标距离。 构造导航向量场f(x,y): (20) 对式(19)求导得 (21) 3.2.2 基于Lyapunov的避障向量场 图1 UAV目标感知域 避障势能函数V(X,XU)为 (22) (23) 在上述基础上,当ds>Ra时,避碰势场函数g(x,y)=0,当Rc (24) 式中:ds为障碍物与UAV之间距离;dm为最小UAV安全距离;γ为UAV航向控制量。 3.2.3 基于Lyapunov的融合向量场 作战目标产生导航向量场引导UAV趋近,障碍物产生避碰向量场引导UAV避障。UAV的融合向量场为 V(x,y)=f(x,y)+g(x,y) (25) 4.1.1 细菌位置编码 细菌采用图2所示的矩阵编码,第1行为任务序列,第2行为执行任务的UAV,即一个细菌代表一种任务调度方案。 图2 细菌编码 图2中Tij∈T,表示第i个细菌的第j个任务,Uij∈U表示执行Tij的UAV。为保证细菌生成时,满足约束条件,按图3所示的任务队列,每个目标任务按照侦查、打击、评估依次排序。从目标队列中任选一目标,依次选取任务,并选取功能匹配的UAV,当该目标任务分配完毕,将该目标清除,当队列为空时,即完成初始化。 图3 任务队列 4.1.2 细菌的趋向操作 以目标为单位,借鉴遗传算法的交叉变异[30]进行趋向操作。C(i)为目标个数,细菌i的趋向操作如下: 步骤 1初始化:k=0; 步骤 2任选一个目标x=randperm(M,1),若k>C(i),转到步骤4,否则转入步骤3; 步骤 3将当前细菌种群中适应度最大的个体中目标x对应的任务所在的每一列都复制到细菌i相应目标任务所在列,k=k+1,转步骤2; 步骤 4得到趋向后细菌i′适应度J′,如果J′>J,则输出趋向后细菌i′,否则返回步骤1。 4.1.3 细菌的迁徙操作 细菌迁徙时以目标为单位的,借鉴遗传算法中染色体的交叉变异操作,迁徙流程为: 步骤 1初始化目标值x为1; 步骤 2若x>M,转步骤5,否则进入步骤3; 步骤 3生成一个(0,1)之间的随机数rand,若rand>Pself(i),转入步骤4,否则x=x+1返回步骤2; 步骤 4将细菌i中目标x对应的列元素删除,随机选择符合功能的UAV,按照任务时序要求,插入到细菌i中,x=x+1返回步骤2; 步骤 5将执行迁徙操作细菌i′输出,计算其适应度值J′,如果J′>J,则保留迁徙后细菌i′,否则取(0,1)之间的随机数rand2,若rand2 综上,任务分配步骤如下: 步骤 1初始化参数S,Nc,Ns,Nre,Ne,Ped,iter,i=0; 步骤 2依据第1.2节约束条件进行细菌初始化; 步骤 3依次进行繁殖操作,迁徙操作,趋向操作,i=i+1; 步骤 4若i 假设在UAVUi的任务集合为{T2c,T3c,T4c,T4v,T6v,T7c},Ui在执行完T3c后被对方UAV击毁,则剩余任务集为{T4c,T4v,T6v,T7c},由于任务执行顺序的要求,实际剩余任务集T={T4c,T4a,T4v,T6v,T7c,T7a,T7v},根据任务分配的约束条件,剩余任务可用最小表示集Tmin={T4c,T6v,T7c}表示。 当UAV坠毁时,采用合同网拍卖算法[31],集群对剩余任务的最小表示集进行竞标,具体流程如下: 步骤 1基站将Tmin中任务对剩余UAV公布; 步骤 2各UAV计算在执行完本身任务后继续执行Tmin每一任务所需代价,对完成代价最小的任务进行竞标,每一个UAV只能对一个任务进行竞标,并向基站发出合同请求; 步骤 3基站对比所有合同,选择每一项任务最小代价的UAV执行该任务,并更新T,Tmin; 步骤 4若T为空,结束竞标,否则进行步骤1。 依据如表1所示的测试函数对算法的性能进行测试,其中f1、f2为单峰测试函数,f3、f4、f5为多峰测试函数,f6、f7、f8为固定多峰测试函数。参与测试的函数有BFO、IBFO-1、IBFO-2,遗传算法[30](genetic algorithm,GA)、粒子群算法[31](particle swarm optimization,PSO)、社会蜘蛛群优化算法[32](social-spider optimization,SSO)。对6种优化算法进行30次独立运行试验的结果如表2所示,图4是测试函数的进化曲线图。 表1 测试函数及其相关属性 从表2以及图4可以看出在较少迭代次数下,BFO算法及其改进算法较其他算法而言有较好的收敛能力。就BFO算法而言,IBFO-1算法的收敛性能要强于BFO以及IBFO-2,但在运行时间方面,IBFO-2要明显强于BFO算法以及IBFO-1算法。就UAV编队的任务分配而言,对算法的实时性要求较高,因此这里采用IBFO-2算法。 表2 测试函数运行结果 图4 算法比较示意图 5.2.1 融合向量场的构建 本文的作战区域为1 000 m×1 000 m、6架UAV、12个作战目标、4个障碍物,具体属性如表3~表5所示。建立以A1为中心融合向量场,如图5所示,在A1的向量场下,1号UAV(UAV1)的航迹如图6所示。 表3 UAV属性信息 表4 作战目标属性信息 表5 障碍物相关信息 图5 融合向量场 图6 UAV1航迹 5.2.2 UAV编队任务规划仿真 为了满足实战化需求,加入动态障碍物对UAV执行任务进行干扰。假设UAV可以在盘旋一周过程中完成任务,当UAV到达目标时,目标的前提任务没有完成,则UAV在以目标为圆心,以Rs为半径的圆上盘旋;等待前提任务完成,进行下一步任务操作。UAV的任务分配结果如表6所示;目标的任务执行情况如图7所示,S、E代表开始和结束时刻;任务分配的总体收益曲线如图8所示,不同算法的运行时间如表7所示,其中UAV1~UAV6表示1号~6号UAV。 表6 任务分配结果 图7 任务执行情况示意图 表7 运行时间对比 图8 收益曲线 从任务分配结果可以看出,1号和2号强击机单独完成1、3、4、5、6、7号任务;3号侦察机与6号轰炸机协同完成9、11、12号任务,4号侦察机与5号轰炸机协同完成2、8、11号任务。从图8可以看出任务分配的整体收益曲线在较少的迭代次数下,收益逐渐平稳,IBFO-2算法在收敛精度强于其他算法;从表7可以看出在运行时间上,IBFO-2优于其他算法。综上,选取IBFO-2算法是合适的。 5.2.3 任务重分配 假设2号UAV在执行完T3任务后被敌方摧毁,现根据合同网拍卖算法[33],对剩余任务进行重新超标,则任务重分配结果如图9所示。6号任务由1号UAV执行,7号任务由1号,4号UAV协同完成。 图9 任务重分配路径曲线 本文基于BFO算法进行多异构UAV的任务规划,首先对BFO算法,提出了针对精度与实时性的改进策略,依据任务分配的特点,选取IBFO-2并结合遗传算法的交叉变异操作,进行任务初分配。同时,依据Lyapunov融合导航以及避障向量场,将UAV路径规划实况融入任务分配中。最后,依据合同网拍卖算法,进行任务重分配。仿真实验验证,基于IBFO-2算法,在实时性和收敛精度方面强于其他算法。3 基于Lyapunov向量场的航程估计
3.1 UAV的运动模型
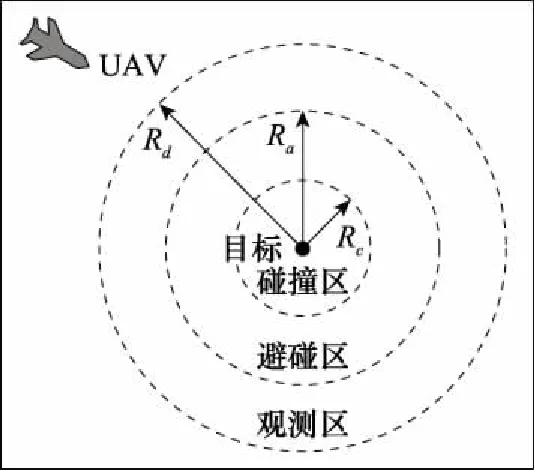
3.2 基于Lyapunov向量场的航迹规划
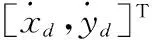

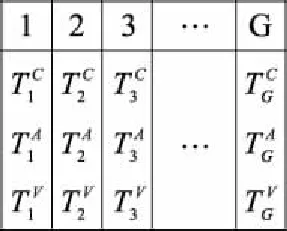
4 多异构UAV任务分配
4.1 基于IBFO-2的任务分配

4.2 基于合同网拍卖算法的任务重分配
5 仿真分析
5.1 BFO算法性能测试


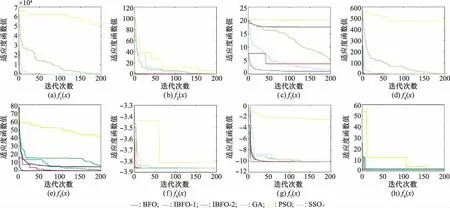
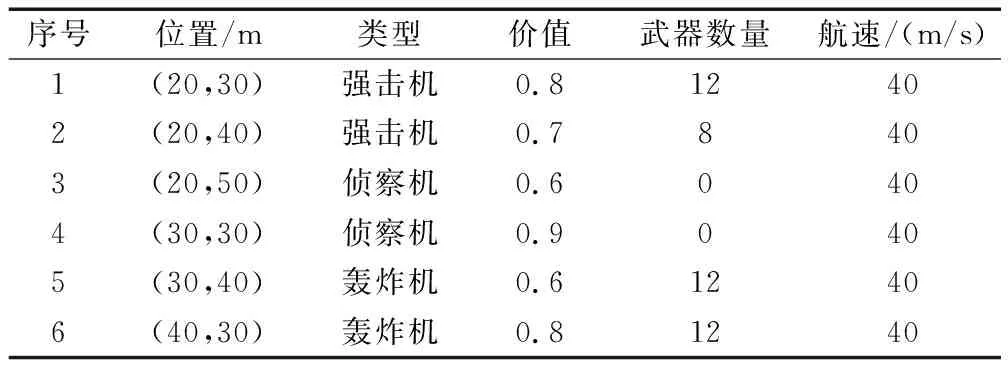
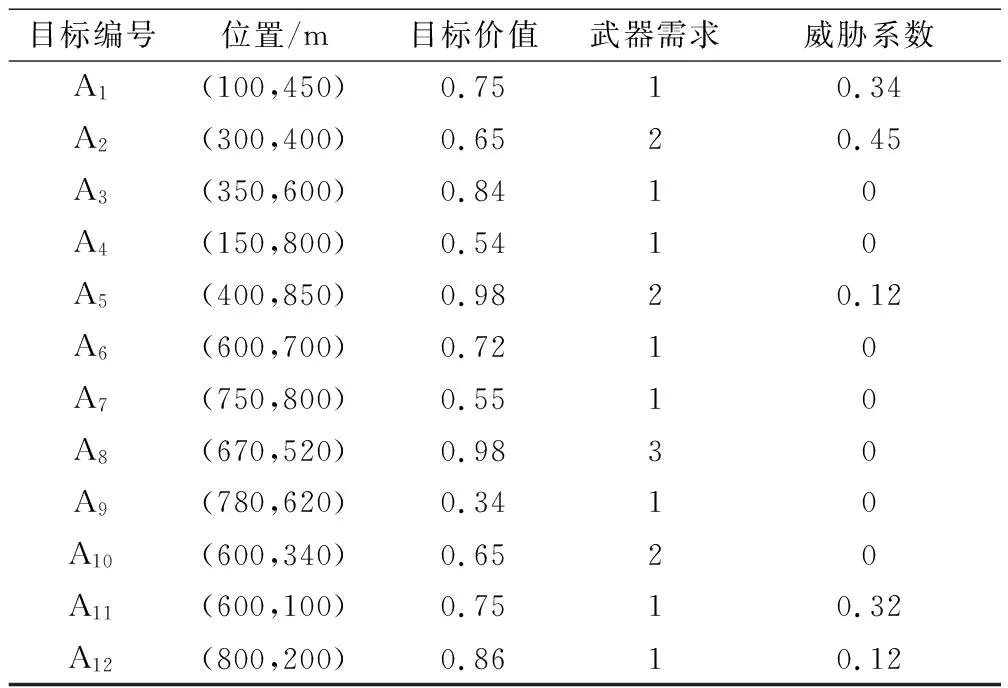
5.2 基于IBFO-2的多UAV任务分配




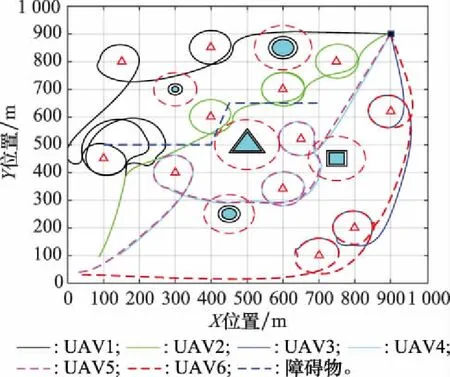

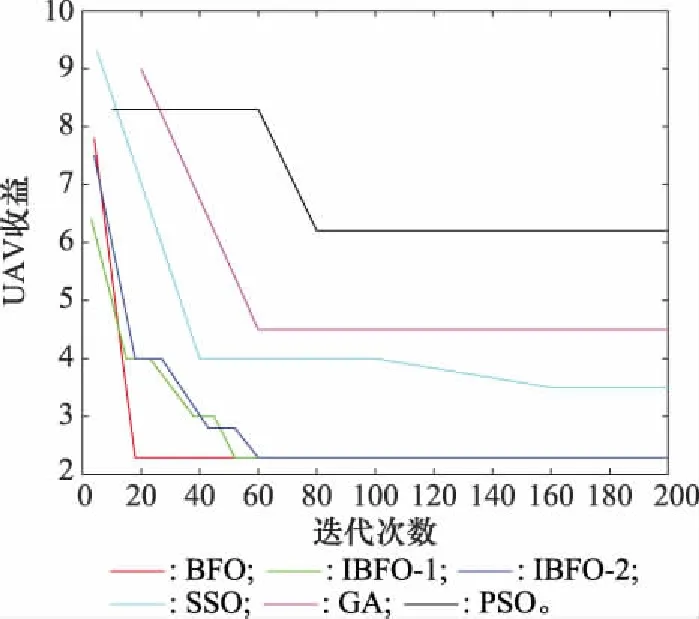
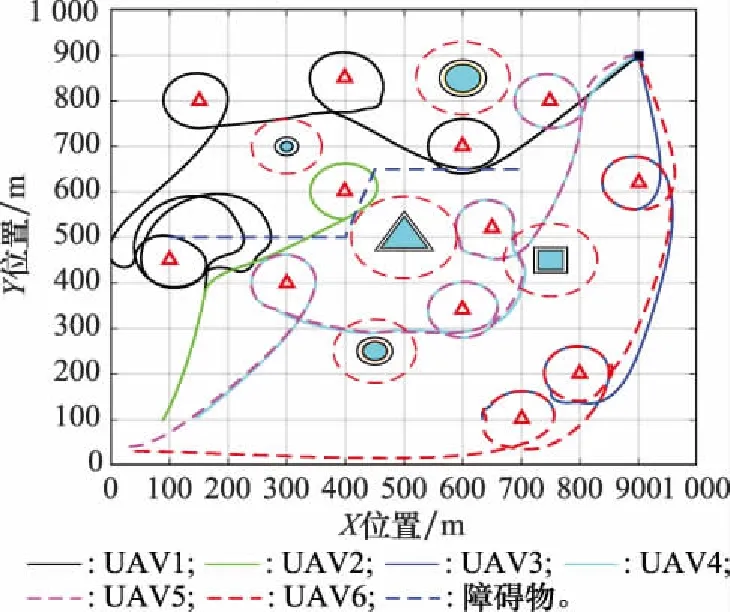
6 结 论
