一种含同轴电缆的线束内部串扰高效分析方法

金奇 盛卫星 韩玉兵 高成 李炎新 张仁李

（南京理工大学电子工程与光电技术学院，南京 210094）

引 言

在电动汽车、卫星等承载复杂电子系统的设备平台上，功能各异的电气和电子装置通过各种电缆束连接，电缆网的布置和设计对于系统级的电磁兼容性(electrimagnetic compability, EMC)至关重要.人们在多导体传输线(multi-conductor transmission line,MTL)理论[1]的基础上，将任意电缆束分解成不同二维截面的串联线段，计算每个线段的单位长度参数矩阵，生成等效电路，从而实现电缆束的EMC分析[2].如今，已有应用了等效电路法的商业软件可以用于电缆网的EMC分析，如FEKO和CST.但是，由于等效电路法忽略了高阶传播模式和电缆的电磁辐射，使得该方法在高频的布线问题上存在局限[3]，比如电缆束的离地高度会影响仿真精度.一方面，由于多导体电缆束的复杂性和计算能力的限制，将电缆网完整建模然后用三维电磁仿真软件直接分析的方法并不常用.于是Andrieu等人提出了一种降低电缆束复杂性的等效线束法(equivalent cable bundle method,ECBM)[3]，通过将相似性质电缆简化为一根电缆后建模的方式，大大减少所分析的电缆数目，实现快速的电缆束分析.目前，该方法已被应用在了单芯线组成电缆束的场路耦合[4]和串扰[5]，以及双绞线组成电缆束的串扰[6]等问题上.同轴电缆上的信号或能量往往对EMC的要求更高，所以对含同轴电缆的电缆束内部串扰问题的分析非常重要.但目前还没有ECBM在含同轴电缆的电缆束上应用的研究.

另一方面，由内外导体组成的同轴电缆因为其良好的抗干扰能力而被广泛地应用于高频和高功率领域.在实际的应用中，为保证电缆在布线过程中的柔软性，其外导体通常采用编织线组成的屏蔽层.但是由于编织层存在小孔和缝隙，屏蔽层的内外表面之间存在耦合现象.Schelkunoff[7]提出用表面转移阻抗来描述这一物理现象，以衡量编织屏蔽层的屏蔽效能.后面经过Kley[8]等作者的努力，表面转移阻抗与编织同轴电缆的各项参数联系在了一起，实现了与测量结果近似的表面转移阻抗理论计算.表面转移阻抗虽然能反应出编织屏蔽层的屏蔽效能，但却不能直观地反应出同轴电缆的屏蔽效能，也不能直接应用于电磁数值计算算法.因为同轴电缆的屏蔽效能不仅与编织同轴电缆的各项参数有关，还与电缆长度、离地高度，以及屏蔽层的接地情况等因素有关.为了能够将表面转移阻抗理论计算与电磁数值计算算法结合起来，人们开始研究表面转移阻抗与屏蔽层表面电流的关系.首先，一种用于将同轴电缆内导体、屏蔽层和外部环境区分开的“三导体系统”被提出[9].在这个系统中，同轴电缆被分为内外两个传输线，并且屏蔽层表面上的电流也分为内表面电流和外表面电流.然后，利用表面转移阻抗将二者联系起来[10]，使用MTL理论建立内传输线电路与外传输线电路的关系.根据对同轴电缆特征阻抗和终端负载的分析，进一步总结出了一组同轴电缆的内外传输线(internal and external transmission line, IETL)转移矩阵[11]，来简化同轴电缆相关问题的计算流程.相比于直接建立完整的同轴电缆编织层模型[12]，这种等效方法能够大大地减少分析时间.

本文提出了一种简化含同轴电缆线束内部串扰的高效分析方法.该方法首先利用IETL转移矩阵将电缆束中的同轴电缆转化为单芯线，然后结合ECBM进一步地简化、减少需要分析的单芯线数量.简化后的模型可以直接用于任意三维电磁仿真软件中进行该电缆束的仿真分析，而无需考虑基于经典传输线理论的等效电路法的局限性.通过电缆束内的串扰仿真比较验证了该方法的有效性.

1 三导体系统和表面转移阻抗

将同轴电缆的外部环境视为一个导体，可以得到一个由同轴电缆内导体、屏蔽层和外部环境组成的“三导体系统”.将屏蔽层分为内表面和外表面，内表面与内导体组成内传输线电路，外表面与外部环境组成外传输线电路，则可以得到如图1所示的同轴电缆等效传输线模型.

图1 同轴电缆等效传输线模型Fig.1 Equivalent transmission line model of coaxial cable

图1所示的是一根长度为L的同轴电缆.其近端(z=0) 连接内阻为Z1S的 激励源，远端(z=L)连接负载，其阻值为Z1L.由于同轴电缆的屏蔽层会根据实际的工程情况决定是否接地，所以使用两个等效阻抗表示接地情况.当近端屏蔽层接地时，Z2S=0，反之，Z2S=∞.同理，当远端屏蔽层接地时，Z2L=0，否则Z2L=∞.可以看出，作为内电路电流的I1(z)可以视为激励源产生的差模电流.由于内电路的实际回路面积很小且结构对称，外界辐射很难产生差模电流，差模电流也很难向外辐射，所以在有关电磁辐射的计算中，差模电流的影响可以被忽略.另一方面，由于屏蔽并不理想，内电路会与外电路耦合产生共模电流，也就是外电路电流I2(z).对于同轴电缆被照射的情况，则是外部干扰在外电路上感应出I2(z)，再通过屏蔽层耦合到内电路产生I1(z).

要确定内外电路的电压和电流的耦合关系，就需要定量地分析同轴电缆屏蔽层的泄露情况.这通常用表面转移阻抗衡量.表面转移阻抗是指屏蔽层上注入电流后，在屏蔽层内表面产生的电压降与这个电流的比值[13].根据互易定理，也可以表示为内导体注入电流后，在屏蔽层外表面产生的电压降和这个电流的比值.所以，同轴电缆表面转移阻抗的单位为Ω/m，表达式为

式中： dV1T(z) 表 示屏蔽层内表面电压降； dV2T(z)表示屏蔽层外表面电压降.通过表面转移阻抗，就可以定量地分析同轴电缆屏蔽层的泄露程度.不同参数的同轴电缆对应表面转移阻抗不同，可以使用三同轴法等方法测量得到[14]，也可以根据编织屏蔽层的参数得到理论计算值.为了更加方便地进行理论验证，文章采用了Kley屏蔽层模型[8]计算表面转移阻抗.

图2中展示了编织带锭数N为12，每一锭内编织线数量为n的编织屏蔽层模型.编织线的丝径为d，编织带的宽度就是nd，α表示编织角.电缆内绝缘体的外径为D，则屏蔽层的平均外径Dm=D+2.5d.经过计算可以得到填充因子和光学覆盖率分别为：

图2 典型编织屏蔽层展开图Fig.2 Typical braided shield

在Kley模型中，表面转移阻抗的完整表达式为

式中：Zd为屏蔽层阻抗，由屏蔽层的直流电阻和趋肤效应决定；Ml为小孔耦合电感，由屏蔽层上的菱形小孔引起；Mg为编织电感，由不同编织带交叠产生；另外，磁场在有孔洞的表面和编织带的缝隙上会形成涡流，这一现象由趋肤电感Ls体现.

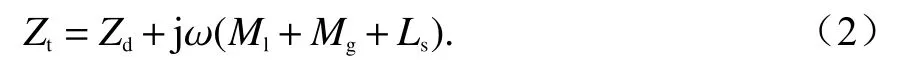
屏蔽层阻抗Zd的 表达式为

式中： σs为屏蔽层材料的电导率；为Kley计算得到的丝径近似值； δs=(πfµsσs)−1/2为屏蔽层趋肤深度， µs为屏蔽层材料的磁导率.

计算小孔耦合电感M1，需要将菱形小孔近似为椭圆[15].厚度为0的椭圆小孔耦合电感Me的表达式为

式中：ϵ为椭圆的离心率，

K(ϵ)和E(ϵ)分别为第一类和第二类椭圆积分，

另外，Ml还需要考虑厚度和屏蔽层弯曲带来的影响，所以

编织电感Mg的表达式为

趋肤电感Ls的表达式为

式中:

需要注意的是，由于Kley模型等表面转移阻抗的理论计算值是通过拟合实测的表面转移阻抗曲线的方式得到的，所以高频情况下会存在一些误差.

2 同轴电缆的IETL转移矩阵

考虑到屏蔽层上的耦合关系后，根据MTL理论，内外电路的传输线方程可以表示为：

式中：V1(0) 和I1(0)为同轴电缆近端上加载的激励源；V2(0)和I2(0)为外部干扰在同轴电缆近端上感应出的电压和电流； ϕ(z2−z1)被称为链参数矩阵或者状态转移矩阵，

式中：γ为该传输线的传播常数；ZC为该传输线的特征阻抗.式(3)和式(4)中的z)和便是IETL转移矩阵.在IETL转移矩阵中，除了有与编织电缆的编织参数相关的表面转移阻抗Zt，还包含表示IETL电路的电压电流关系的转移矩阵[11].

通常，同轴电缆的内电路两端负载与同轴电缆内传输线的特征阻抗Z1C匹配，即Z1S=Z1L=Z1C.此时，外电路对内电路耦合的可以表示为

式中：

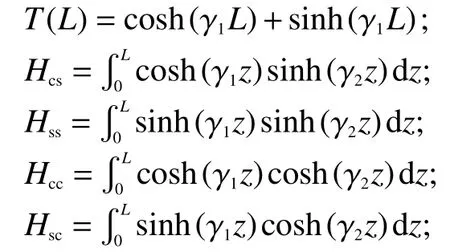
第一种情况，如果屏蔽层两端良好接地，即Z2S=Z2L=0 ，那么(z)可以表示为

第二种情况，如果屏蔽层两端不接地，即Z2S=Z2L=∞， 那么可以表示为

第三种情况，如果屏蔽层只有远端良好接地，即Z2S=∞ ，Z2L=0 ，那么z)可以表示为

第四种情况，如果屏蔽层只有近端良好接地，即Z2S=0，Z2L=∞.那么可以表示为

通过上述IETL转移矩阵可以将同轴电缆等效为单芯线，其内导体直径等于屏蔽层外径，护套厚度为同轴电缆护套厚度.

3 等效线束法(ECBM)

ECBM的思路是将一捆电缆束中的电缆按两端负载与共模阻抗的比较分为4组，然后将每组电缆等效为一根电缆.等效的过程中需要将原单位长度电感矩阵L和电容矩阵C简化为简化电感矩阵Lr和电容矩阵Cr，用来计算等效后每根电缆的半径和坐标.

ECBM成立需要满足两个假设[16]：一、在被分析的问题中，被简化的电缆受到的共模干扰远大于差模干扰；二、同一组电缆上的共模电压和电流相同.为了满足第一个假设，李茁等人[17]提出将串扰中的干扰电缆和受扰电缆单独分组来实现电缆束内的串扰问题分析.第二个假设的等价条件是同一组的电缆有相同特征阻抗.为了方便推导，下面以平行金属板放置由N根电缆组成的电缆束为例，介绍ECBM的步骤.

第一步，利用二维电磁数值计算软件得到该电缆束的单位长度电感矩阵L和电容矩阵C.电缆束的相关问题可以近似为在无损非均匀介质中理想导体的问题.那么，该多导体传输线的单位长度阻抗矩阵Z和导纳矩阵Y可以近似为Z=jωL和Y=jωC.然后，可以计算得到共模阻抗Zcm.

第二步，将电缆按两端负载与Zcm的比较分为4组，规则如表1.再根据分组简化单位长度电感矩阵L和电容矩阵C.

表1 电缆分组规则Tab.1 Rules for cable grouping

除去编号分别为N−1和N的干扰电缆和受扰电缆后剩下的电缆分组如下：第一组的编号为g1=[1,···,α]， 共N1个 ；第二组的编号为g2=[α+1,···,β]，共N2个；第三组的编号为g3=[β+1,···,γ]， 共N3个；第四组的编号为g4=[γ+1,···,N−2]， 共N4个.算上干扰电缆和受扰电缆，总共6组.

将每组导体近似为共模模式进行等效，且由第二个假设可以得到各组内流过每根电缆的电流大小相等，即每组等效的端口共模电压和端口共模电流满足：

其他分组类似.根据MTL公式[1]

可以得到分组后的第一组对应传输线公式为：

其他分组类似.式中：

其他矩阵类似.

将式(13)两边同时左乘 [11 ···1]1×N1/N1，可得到

同理，将式(14)同时左乘 [11 ···1]1×N1/N1，可得到

其他分组类似.将所有等式综合整理后，可得简化导纳矩阵Yr和 简化阻抗矩阵Zr的关系式为：

式中：

那么，简化电感矩阵Lr和简化电容矩阵Cr分别为：

第三步，根据简化矩阵得到新的电缆束截面.具体步骤如下：

1)计算每个等效导体相对于地面参考的高度hi，使其与原电缆束的几何形状一致，即hi等于对应组的所有导体高度的平均值.

2)根据Lr中等效导体的自感Lii计算出等效导体的半径ri，公式为

3)等效导体i和j之间的距离dij可以通过互感Lij得到，公式为

4)由于第二步和第三步采用的解析公式都是近似解，所以通过前三步得到的截面计算出的单位长度电感矩阵与简化电感矩阵并不相同.还需要通过优化来调整hi、ri、dij，实现二者匹配.

5)通过优化确定所有电缆的护套厚度，使截面计算出来的单位长度电容矩阵与简化电容矩阵近似.

6)计算等效导体两端的负载阻抗.由于忽略差分干扰的影响，可以认为各电缆只与接地面有负载连接.那么，等效导体的负载阻抗为分组内导体负载并联后的值，即

经过以上步骤，完成了对全单芯线电缆束的简化.

4 含同轴电缆线束内部串扰分析

为验证本文方法的有效性，下文给出一个算例进行仿真比较.

在金属平板上水平架设了1 m长的电缆束，由2根同轴电缆，7根单芯线组成.电缆连接在高度为100 mm的金属托架上，电缆束中心位置离地50 mm，如图3所示.其中，单芯线的内导体半径为0.372 5 mm，护套厚度为0.14 mm.同轴电缆型号为RG174，其内导体半径为0.24 mm，内绝缘体的厚度为0.5 mm，屏蔽层由16锭铜丝线束编织而成，编织角为30°，编织线束由5根直径为0.1 mm的编织线组成，护套厚度为0.5 mm.导体材料均为铜，护套和内绝缘的材料均为PVC.将上述信息代入式(2)中，即可算出该同轴电缆的表面转移阻抗.以金属平板中点为原点，各根电缆的分布坐标如表2所示，该电缆束的截面如图4所示.

图3 水平架设的电缆束Fig.3 Horizontal cable bundle

表2 电缆分布坐标Tab.2 Distribution coordinates of cables

图4 电缆束截面图Fig.4 Sectional view of the cable bundle

把同轴电缆的表面转移阻抗和分布坐标信息代入IETL转移矩阵公式，即可将同轴电缆转化为单芯线，其内导体直径为1.98 mm，新的截面如图5(a).各电缆的终端负载电阻大小如表3所示，其中屏蔽层接地等效为10−3Ω，不接地等效为106Ω.

图5 简化后的电缆束模型Fig.5 Simplified cable bundle model

该电缆束的单位长度电感矩阵L和电容矩阵C为：

设定电缆1为组1干扰电缆，电缆9为组2受扰电缆，余下电缆根据表3被分为4组，具体如下.

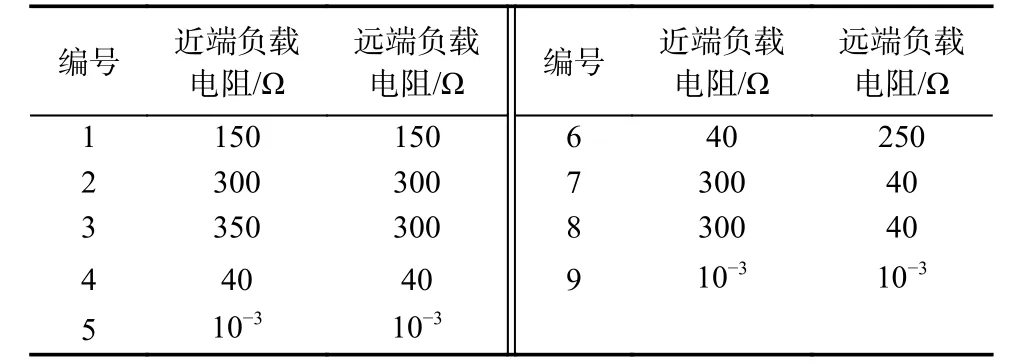
表3 电缆束终端负载电阻Tab.3 Terminal loads of the cable bundle

组3：电缆2-3；

组4：电缆4-5；

组5：电缆6；

组6：电缆7-8.

利用式(17)和(18)得到简化电感矩阵Lr和电容矩阵Cr(排列顺序为从组1到组6)为

将Lr代入式(19)和(20)，计算得到等效电缆束的截面，可以得到图5(b)中的电缆束，其中G1、G2、G3、G4分别对应组3、组4、组5、组6.

在基于有限元法(finite element method, FEM)的HFSS软件中分别建立利用IETL建模的全单芯线电缆束模型和利用IETL与ECBM建模的等效电缆束模型，如图5所示.在干扰电缆的远端加上正弦激励，幅度为1 V，仿真得到流经干扰电缆和受扰电缆的电流I1和I9.再利用式(3)和(6)计算出受扰同轴电缆内导体上串扰造成的电流.将计算结果与采用等效电路法和有限积分技术(finite integration technique,FIT)的CST软件仿真结果对比，如图6所示.图中黑色实线为CST仿真的原电缆束模型中受扰同轴电缆的串扰电流，蓝色虚线为HFSS仿真的采用了IETL转移矩阵的全单芯线电缆束模型中受扰同轴电缆的的串扰电流，红色点划线为HFSS仿真的采用了IETL转移矩阵和ECBM的等效电缆束模型中受扰同轴电缆的的串扰电流.可以看出，三种方案仿真得到的串扰电流曲线吻合良好.在HFSS中仿真全单芯线电缆束耗时为5 h 59 min，仿真等效电缆束模型耗时为3 h 55 min.这说明采用ECBM能够有效降低仿真时间.

图6 受扰同轴电缆的串扰电流Fig.6 Crosstalk current of the victim coaxial cable

在CST的Cable Studio模块中仿真原电缆束模型运用了等效电路法和FIT算法，并使用Kley模型计算同轴电缆的表面转移阻抗.一方面，由于等效电路法忽略了高阶传播模式，而Kley模型又是拟合表面转移矩阵低频部分的曲线，所以仿真结果在高频部分会存在一些误差.另一方面FIT数值计算算法采用Yee氏网格剖分仿真空间，网格大小和数量会影响仿真的速度和精度.好在已经有诸多文献[18-20]通过与实测数据的比较，验证CST的电缆仿真结果是可靠的.

为了进一步验证文中提出的仿真方法的有效性，将CST的仿真结果作为可信赖数据集，利用特征选择验证法(feature selective validation, FSV)[21]比较IETL转移矩阵和ECBM对仿真结果的影响，统计结果如图7所示.

图7 FSV分析得到的置信直方图Fig.7 Confidence histogram obtained from the FSV analysis

图中蓝色柱表示CST与采用三维建模和FEM算法的HFSS在受扰同轴电缆屏蔽层上感应电流的仿真结果上的差别，此时IETL转移矩阵和ECBM均未对仿真结果产生影响.可以看出，评价等级为“极好”的数据所占比例也超过75%，仿真结果的相似度依然很高.这部分的误差主要是由于两款软件采取了完全不同的数值计算算法和网格剖分引起的.

图中红色柱表示应用了ECBM后，HFSS和CST中受扰同轴电缆屏蔽层上感应电流的仿真结果的差别.比较蓝色柱和红色柱，可以看出ECBM对仿真结果有一定影响.

图中黄色柱表示应用了IETL转移矩阵后，HFSS和CST中受扰同轴电缆内部导体上的感应电流的仿真结果的差别.比较蓝色柱和黄色柱，可以看出IETL转移矩阵对仿真结果的影响很小，只产生少量“不好”的数据.

图中紫色柱表示应用了IETL转移矩阵和ECBM后，HFSS和CST中受扰同轴电缆内部导体上感应电流的仿真结果的差别.将紫色柱与蓝色柱和黄色柱比较，可以发现相比于ECBM的影响，IETL转移矩阵造成的误差可以忽略不计.而ECBM产生“不好”的数据所占比例也不超过10%，并且谐振频率和带宽等关键信息依然可以获取.另一方面，采用ECBM能够有效降低仿真的复杂度，节约大量的仿真时间.说明文中提出的方法在分析同轴电缆串扰问题时是有效且有意义的.

5 结 论

本文通过将IETL转移矩阵和ECBM结合，提出了一种分析含同轴电缆线束内串扰的高效方法.先将含同轴电缆的电缆束转化为全由单芯线组成的电缆束，然后使用ECBM将全单芯线的电缆束进一步简化为等效电缆束模型.利用该模型能够高效地分析干扰电缆和受扰电缆间的串扰.文中使用两种基于不同数值计算算法的软件分别仿真并比较了原电缆束模型和等效电缆束模型中同轴电缆内串扰电流大小，再通过FSV评估方法比较各种仿真结果的差别，从而验证了提出方法的准确性，仿真耗时的比较结果也说明了ECBM有效地提高了仿真含同轴电缆线束相关问题的效率.而且，相比于等效电路法，由于本方法是三维建模仿真，所以在高频的布线问题上不存在限制.

但是，由于IETL转移矩阵本身只考虑了三导体系统，而事实上电缆束是一个多导体系统.对于以同轴电缆为干扰电缆的情形，IETL转移矩阵的公式并不能准确地计算出电缆束中该同轴电缆屏蔽层上的感应电流，这仍需要进一步的研究.