基于三角覆盖MF-DFA的环形零件图像种类特征研究

盛文婷，王幸，赖科学，何涛

（1.湖北工业大学机械工程学院，湖北武汉430068；2.湖北工业大学现代制造质量工程湖北省重点实验室，湖北武汉430068）

我国是制造业大国，零件作为制造域中最基本的组成单元，在制造域中具有举足轻重的地位[1]。有效地进行零件种类识别是制造域中不可或缺的环节。近年来，快速发展的图像识别技术正好可以解决这一问题[2]。零件图像种类特征提取作为零件种类图像识别的关键步骤，在制造域中极其重要。

目前，常用的零件图像特征提取方法是利用图像处理算法从图像中获取零件的几何与纹理特征[1,3]。然而，近几年新兴的多重分形可以考虑物体在形成过程中各种不同层次的特征，能够更加全面有效地对物体进行描述[4-5]。在多重分形算法中，MF-DFA 能较好地反映非线性与非平稳对象不同尺度的特性[6]，但存在过度覆盖的缺点。

因此，文中对MF-DFA 略作改进，提出一种可以减少过度覆盖的三角覆盖MF-DFA，用于描述具有分形特性的环形零件图像的种类特征，并利用SVM 对所得的种类特征进行识别验证。验证结果表明该方法可以准确表达环形零件图像的种类特征。

1 三角覆盖MF-DFA

1.1 MF-DFA算法

多重分形是由多个标量指数的奇异测度所组成的集合。它使用一个谱函数从对象的部分出发，根据自相似性质，来研究其最终的整体特征[7]。MFDFA 是Kantelhardt 等人在(Detrended Fluctuation Analysis,DFA)的基础上提出的一种非平稳时间序列多重分形特征分析方法。该方法能快捷地计算出一维数据的多重分形谱，并进行有效的多重分形特征分析[8-9]。

随着MF-DFA 应用域的拓展，MF-DFA 已被推广至二维以及高维数据中[10]。该次研究对象为环形零件图像，因此选用的算法为二维MF-DFA。二维MF-DFA 对于大小为M×N的矩形序列x(m,n) (m=1,2…,M,n=1,2…,N)进行分析的具体流程如下：

1）对x(m,n)构造去均值的和序列Y(i,j)。其中，i=1,2,…,M,j=1,2,…,N，为序列x(m,n)的平均值。

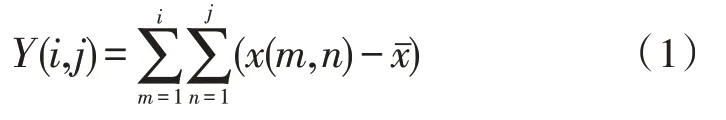
2）如图1所示，使用边长为s的正方形模块，对Y(i,j)从其左上角开始，从左至右、从上至下进行覆盖，将序列Y(i,j) 分成Ms×Ns(Ms=[M/s],Ns=[N/s]) 个互不重叠的小正方形区域，每个区域均包含s×s个数据。由于M与N不一定被s整除，为防止数据的遗漏，需从序列Y(i,j)其他3 个角开始再次进行覆盖，共得到4Ms×Ns个小正方形区域(w,v)(w=1,2,…,2Ms,v=1,2,…,2Ns)。

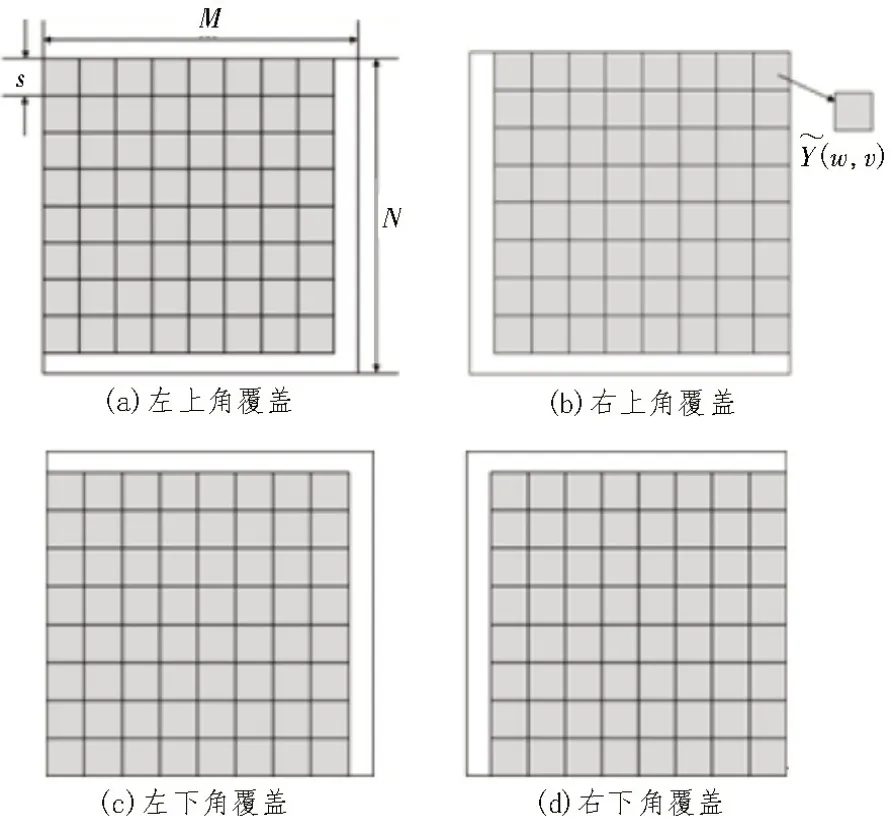
图1 二维MF-DFA覆盖

3）依次对4Ms×Ns个小区域(w,v)内的s×s个数据使用最小二乘法进行二元多项式拟合，如式（2）所示。其中，i=1,2,…,s,j=1,2,…,s。

4）计算均方误差F2(s,w,v)。

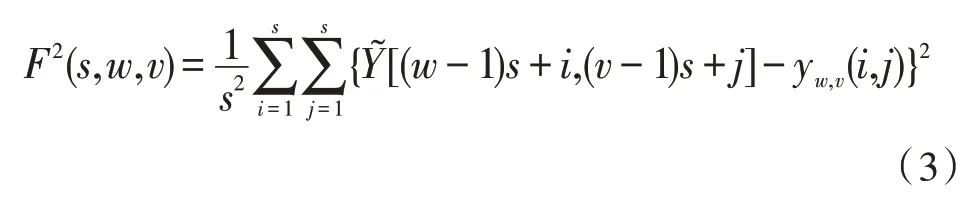
5）对于4Ms×Ns个区域，计算q阶测度波动函数Fq(s)。

Fq(s)是关于模块边长s与分形阶数q的函数，随着s的增大，Fq(s) 呈幂律关系增加，即Fq(s)∝sh(q)。h(q)为Hurst 指数。它与奇异指数α、奇异谱f(α)之间存在以下关系：

6）重复步骤5），不断改变正方形模块的边长s，获得一组不同尺度s下的测度波动函数Fq(s)，对s和Fq(s)取对数得到log(s)和log(Fq(s)) 。将两者进行线性拟合得到h(q)，并代入式(5)中计算，即可获得x(m,n)的多重分形谱α-f(α)。

1.2 三角覆盖MF-DFA算法

根据1.1 节可知，在二维MF-DFA 中，通常使用正方形模块对二维序列进行覆盖。这样会使得图像中图形轮廓占据正方形模块区域不够充分，造成过度覆盖。因此，文中使用三角形模块进行覆盖。

此外，二维MF-DFA 通常使用二元多项式拟合计算测度波动函数Fq(s)。二元线性拟合运算的时间复杂度远大于一元线性拟合。因而，三角覆盖MF-DFA 选用一元线性拟合来计算Fq(s)。三角覆盖MF-DFA 对于大小为M×N的二维矩形序列x(m,n)(m=1,2,…,M,n=1,2,…,N)进行分析的流程如下：

1）根据式(1)对x(m,n)构造去均值的和序列Y(i,j)。

2）取边长为r的正方形模块(r为偶数，4 ≤r≤W，W=min(M,N))。如图2中的阴影部分所示，对正方形模块进行分块，分成4 个大小相同，方向不同的等腰三角形模块。模块1 位于正方形模块的右上方。将模块1 分别顺时针旋转90°、180°、270°即可获得模块2、3、4。其中h为三角形模块的高度，h=r/2(2 ≤h≤W/2)。每一个模板面积占正方形模块面积的1 4。

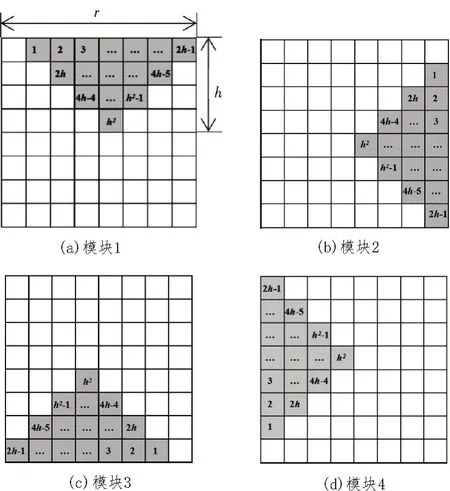
图2 三角形覆盖模块与序号标注

3）如图3所示，用这4 种模块对Y(i,j)从其左上角开始，从左至右、从上至下进行覆盖，获得4Mr×Nr(Mr=[M/r],Nr=[N/r]) 个互不重叠的小区域。每个区域均包含s(s=h×h)个数据。由于M与N不一定被r整除，为防止数据遗漏，从Y(i,j)其他3 个角开始再次进行划分，共得到Ns(Ns=16Mr×Nr)个小三角形区域˜(v)(v=1,2,...,Ns)。如图2所示，将每个小区域内的s个像素点依次进行序号标注。

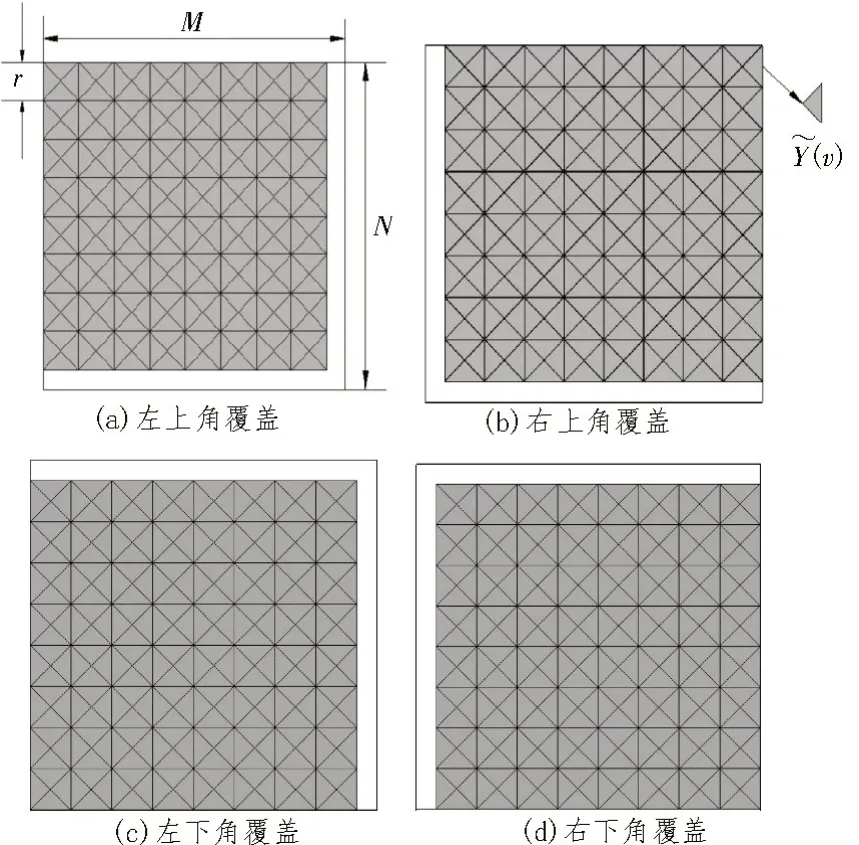
图3 二维三角MF-DFA覆盖

4）分别对Ns个小区域˜(v)内的s个像素点的灰度值与其对应的序号k(k=1,2,…,s)使用最小二乘法进行一元一次多项式拟合。

5）计算均方误差F2(s,v)

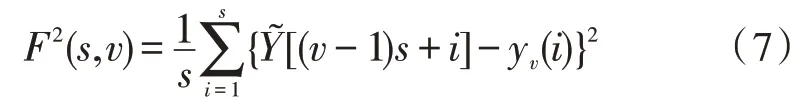
6）对Ns个区域，计算q阶测度波动函数Fq(s)。

7）重复步骤6），不断改变三角形模块的高h，获得一组不同尺度s下的测度波动函数Fq(s)，对s和Fq(s)取对数并进行线性拟合得到h(q)，代入式(5)中计算即可得到x(m,n)的多重分形谱。

为了清楚显示三角形模块覆盖优于正方形模块覆盖。该文设计了一个验证性对比实验。如图4所示，对一条不规则且具有一定自相似的二维图形，分别用正方形模块和三角形模块进行覆盖。并分别计算出覆盖该图形所需正方形模块面积S1与所需三角形模块面积S2占整幅图像面积S的比率η1与η2(η1=S1/S,η2=S2/S)。

经计算得η1=73.44%,η2=61.33%(η1＞η2) 。因此，三角形覆盖方法在保证图像完全覆盖的情况下，解决了过度覆盖的问题，提高了图像覆盖的精度。

2 环形零件图像种类特征研究

2.1 研究对象选择

如图5所示，在常见环形零件中齿环、齿轮、轴承与螺母都由自身的结构单元重复组成，并且存在突出的不规则和一定自相似性的特征，即分形特性。因此选用这四类环形零件的图像作为研究对象。在图6所示的环形零件图像采集系统中，采集四类环形零件图像，它们的原始图像如图7所示。

图5 环形零件自相似性质

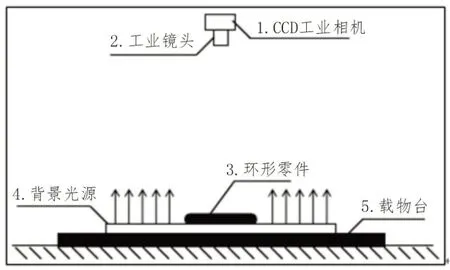
图6 环形零件图像采集系统

2.2 环形零件图像种类特征分析

如图7所示，原始环形零件图像中背景区域偏白，零件区域偏黑，零件区域内像素点的灰度值远小于背景区域内像素点的灰度值。此外，受拍照环境的影响，原始环形零件图像中存在少量噪音光斑。它们均会对多重分形谱的计算结果造成影响。所以在计算前需对图像进行预处理。预处理分为4 个步骤，分别是二值化、面积滤波、零件区域灰度值还原与零件区域灰度值取反。

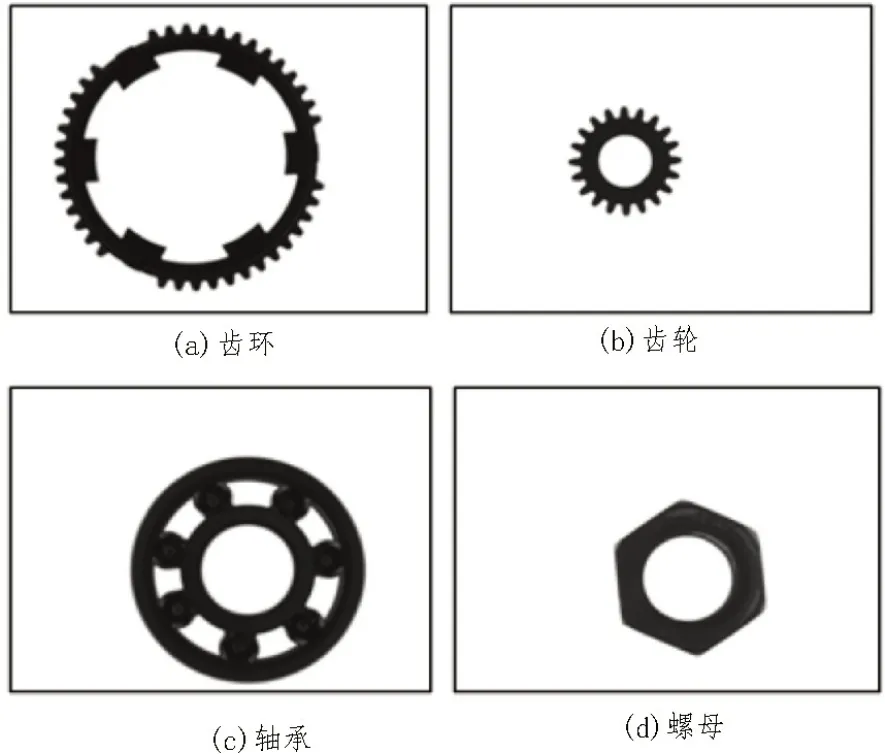
图7 环形零件原始图像

环形零件预处理图像如图8所示。此时，图像中无噪音光斑，零件区域偏白，背景区域偏黑，零件区域内像素点的灰度值远大于背景区域内像素点的灰度值。图像零件区域的特征被完美保留并且非常突出。至此，图像预处理工作结束。

图8 环形零件预处理图像

由于单张环形零件图像的多重分形谱无法完美诠释环形零件图像的整体特征。分别将四类环形零件在图6所示系统中以不同的位置形态各采集100张图像，使用1.2 节中的三角覆盖MF-DFA 计算它们的多重分形谱，用于环形零件种类特征研究。

计算过程中，理论上分形阶数q的取值范围越大越好，但是随着取值范围的加大，所需的计算量与运算时间均会增加。综合考虑，q的取值范围是-10.5～10.5，取值间隔为0.2。因此，每张图像的多重分形谱上有106 个点，每个点具有横纵两个坐标，共包含212 个数据。

将计算好的齿环、齿轮、轴承与螺母图像的多重分形谱分别以不同形状的谱线绘制于图9(a)中。观察图9(a)可知，在四类环形零件图像谱线顶点的右侧，四类环形零件图像谱线交错重叠，杂乱无章，种类特征不明显。而在谱线顶点的左侧，如图9(a)中黑色虚线框所示，同类环形零件图像的谱线各自成束，非同类环形零件图像的谱线虽有少许相交但大致错开，种类特征较为明显，易于区分。

如图9(b)所示，选择四类环形零件图像的每根谱线中位于各自谱线顶点左侧区域的数据作为环形零件的种类特征数据。在环形零件种类特征数据中，每张环形零件图像对应一根短谱线，每根短谱线上均有53 个点，共包含106 个数据。

2.3 环形零件图像种类特征值提取

根据图9(b)可知，环形零件种类特征数据呈非线性，来自400 张环形零件图像，每张图像均有106个数据。即特征数据的维度为106，可以组成一个大小为400×106 的矩阵A。由于A的维度较高，不利于识别验证，需进行降维处理。

图9 种类特征分析

在降维算法中KPCA 既可以达到数据降维的目的又兼顾了非线性的问题，适合非线性特征提取[11]，选用KPCA 用于降维。

2.3.1 KPCA

KPCA 的基本思想是利用核函数，将原始低维空间数据通过非线性变换映射到高维特征空间F。在F中使用线性主成分分析(Principal Component Analysis,PCA)提取数据的特征值[11-13]。

KPCA 对于样本数据集X={x1,x2,...xm},xk∈RN（N为样本维度，m为样本数量）的降维步骤如下：

1）计算X的核函数K(Kij=ϕ(xi)·ϕ(xj))。由于高斯径向基RBF 核函数计算过程简单，并且预测速度和精度通常优于其他核函数[11]，选用RBF 核函数。其表达式如下所示。

2）根据式（10）中心化处理K获得。其中，

3）对进行特征向量分解，获得˜的特征值λi与特征向量˜。其中，

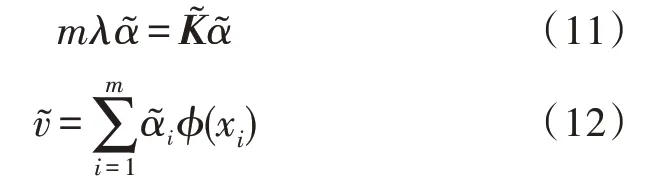
4）将特征值按降序排序得λ′1＞…＞λ′m，并以此调整特征向量的顺序得v1′,…,v′m。

5）将v′1,…,v′m使用施密特正交法获得单位正交化特征向量a1,…,am。

6）计算特征值的累计贡献率B1,…,Bm，当Bt＞0.96 时，则提取前t个特征向量a1,…,at。

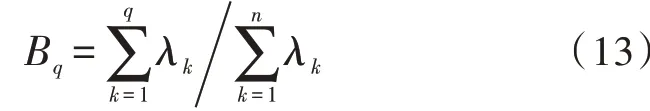
7）计算前t个特征向量的投影Y=·a。a由特征向量ai(i=1,…,t)构成，Y即为通过KPCA 求取的X的主成分。

2.3.2 环形零件图像种类特征值

使用前面所述的KPCA 对A进行降维处理即可提取出环形零件的种类特征值Y。经过KPCA 处理后A的特征值的累计贡献率Bi如图10(a)所示。A在第三个特征值处的累计贡献率B3超过了0.96，因此Y是一个大小为400×3 的矩阵。

图10 种类特征提取

为直观表现环形零件的种类特征，将Y以三维图像的方式展示在图10(b)中，每个三维数据点的位置坐标为每张图像的3 个特征值分量。数据点根据它们对应的环形零件种类组成了4 个群簇，表明环形零件图像种类特征值提取成功。

3 环形零件图像种类识别验证

为证实环形零件图像种类特征值Y能够精确表达环形零件图像的种类特征，在此对Y进行了识别验证。在常用的分类识别方法中，SVM 具有扎实的理论基础和良好的泛化性[14]，选择SVM 用于识别验证。

3.1 Lib-SVM

Lib-SVM 是台湾的林智仁(Chih-Jen Lin)教授于2001年开发的一套操作简单且易于使用的SVM 库。此软件包能够非常方便地对数据进行分类与回归，在物联网与医疗等领域均得到了广泛的应用[15-17]。因此选用Lib-SVM 作为识别验证工具。Lib-SVM 的使用步骤如图11 所示。在第3 步中Lib-SVM 共提供了线性、多项式、高斯径向基(RBF)与Sigmoid 这4 种核函数，选择其一即可，文中选择应用最广的RBF，RBF表达式如式（14）所示。其中σ＞0 为高斯核带宽。

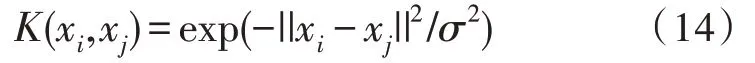
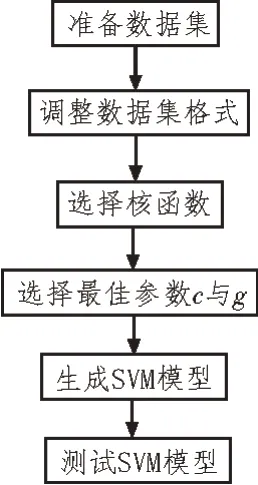
图11 Lib-SVM使用流程

3.2 验证结果

环形零件种类特征值Y来自400 张图像。从Y中每类环形零件100 张图像的种类特征值内各随机抽取50 张图像的种类特征值，将它们整合后作为环形零件图像种类训练数据集D。其余环形零件图像的种类特征值则整合后作为环形零件图像种类测试数据集E。D与E经归一化得到环形零件图像种类标准训练集train_chq 与标准测试集test_chq。train_chq 与test_chq 均是大小为200×3 的矩阵，如图12 所示。

图12 标准训练集与测试集

train_chq 经进行交叉验证获得的最佳惩罚因子c与最佳核函数参数g(g=1/σ2)的值均为2-7。将c、g、train_chq 与test_chq 代入Lib-SVM 中进行训练与分类运算所得的环形零件图像种类识别验证结果如图13 所示。 test_chq 中200 张环形零件图像有199 张图像的零件种类被准确识别[18]。识别预测的准确率(Accuracy)较高为99.5%。证实了三角覆盖MF-DFA 可以良好表达环形零件图像的种类特征。

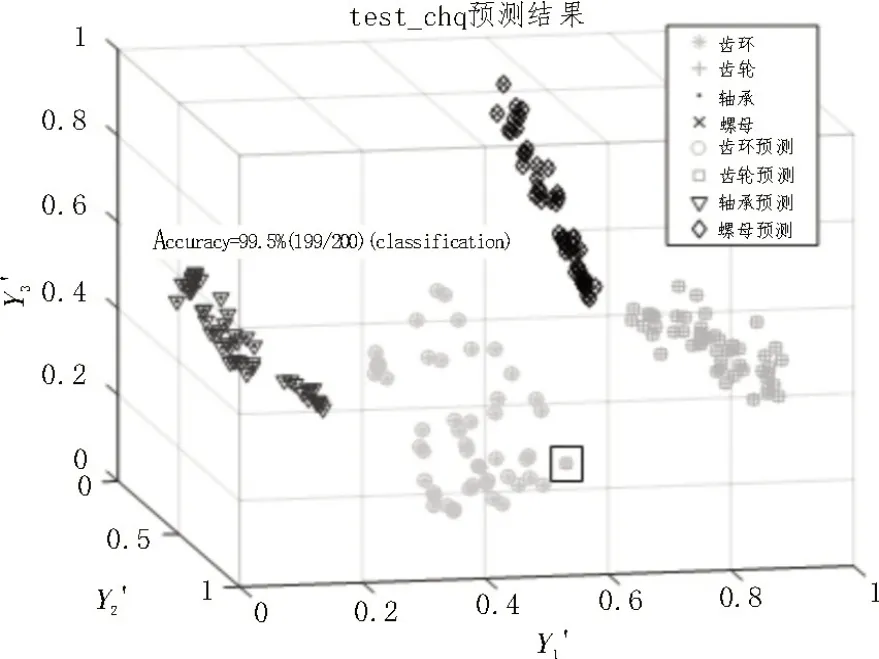
图13 种类验证结果

4 结 论

文中针对MF-DFA 具有过度覆盖的缺点，对其略作改进提出三角覆盖MF-DFA。使用三角覆盖MF-DFA 从全局和局部两方面出发[19]，深层次发掘环形零件图像的种类特征，并得到以下结论：1）根据对比实验验证了三角覆盖MF-DFA 相较传统MF-DFA 的图像覆盖精度更高，解决了过度覆盖问题。2）选用常见且分形特性较好的齿环、齿轮、轴承与螺母这四类环形零件为研究对象，利用三角覆盖MF-DFA 与KPCA 从它们的图像中获取环形零件种类特征值Y。使用SVM 对Y进行识别验证，所得识别准确率为99.5%。证实三角覆盖MF-DFA可以准确表达环形零件图像的种类特征，具有工程应用价值，可应用于工业生产中的环形零件图像的种类识别。