考虑土体非线性特性的散体材料桩复合地基沉降计算

2021-11-10张学飞李全军金丹丹李传勋

地基处理 2021年5期

张学飞，刘聪，李全军，金丹丹，李传勋

（1.江苏省地矿局第三地质大队，江苏镇江 212111；2.江苏大学土木工程与力学学院，江苏镇江 225009）

0 引言

散体材料桩由于造价相对较低、处理效果显著等优势广泛应用于软基处理，以减小软基的沉降变形及增强软土地基的稳定性。因此，散体材料桩复合地基的沉降计算是设计计算的主要内容。目前规范中对散体材料桩复合地基主要采用应力修正法和复合模量法开展沉降计算。

应力修正法是通过应力修正系数计算得到桩间土体承担的应力，进而可通过传统分层总和法计算得到复合地基的沉降值。该方法的成败主要取决于应力修正系数μs的选取。应力修正系数μs与很多因素有关，因此想要得到精确的μs是比较困难的，基于对该问题的认识，刘吉福[1]给出考虑上部填土厚度及弹性模量等因素的桩土应力比表达式。池跃君等[2]研究外荷载作用下的刚性桩复合地基桩体、桩间土体承载力特性，对比分析不同因素对桩土应力比的影响。饶为国和赵成刚[3]推导了考虑置换率、路堤荷载、网的刚度等因素的桩土应力比表达式。以上研究可发现目前对应力修正法的研究大多集中在桩土应力比方面的研究，但需注意的是，即使得到相对合理的应力修正系数，目前规范中的应力修正法仍然不能考虑土体的非线性压缩特性。

复合模量法是目前工程中应用最多且与工程实际结果符合度较好的一种方法，该方法的精确性取决于复合模量的确定。规范中给出的复合模量确定方法是对桩体压缩模量、桩间土体压缩模量按照一定比例复合，但该方法并不能真实反映复合土层复合模量的变化[4]。鉴于此，王凤池等[5]给出考虑桩长、桩端土性质等因素的修正复合模量表达式。郑俊杰等[6]将参变量变分原理应用到复合模量的求解中，给出复合模量在不同状态下的解析解，该解析解还考虑外荷载对复合模量的影响。章定文和刘松玉[7]利用分层总和法计算思路对复合模量进行反算，并引入修正系数α对反算的复合模量进行改进。朱奎等[8]基于剪切位移法及基本假定，给出考虑桩长、桩体模量、桩周土体模量等参数影响的复合模量解析解。以上对复合模量法的研究中，大多认为土体的压缩模量为常数，仍然不能考虑土体具有的典型非线性压缩特性。

事实上，不同深度处土体的有效应力是不一样的，即土体有效应力随着深度的变化而变化，这势必导致土体的压缩模量也在不断变化。因此，有必要在沉降计算中考虑土体的非线性压缩特性。正是基于以上认识，盛崇文[9]根据实际工程的大型载荷试验来确定桩体和桩间土体的压缩模量，进一步提高了碎石桩复合地基沉降计算的可靠性。姜前[10]对载荷试验数据拟合分析得到桩体、桩周土体应力-应变曲线关系，利用应力-应变曲线关系来求解压缩模量，进一步表明用载荷试验确定压缩模量的可行性。杨光华[11]深入分析载荷试验得到的应力-应变曲线关系，给出考虑应力水平的切线模量表达式，通过该表达式得到的切线模量反映土的非线性特点，计算结果更加接近工程实测值。在实际工程中对复合地基进行大型载荷试验的费用较高，一般情况下并不能给出其p-s曲线。针对这一问题，邓文龙等[12]通过土体侧限压缩试验曲线，对比分析不同深度处土体压缩模量Es的变化规律，针对这一变化规律给出考虑深度影响的压缩模量表达式，但该表达式未考虑应力历史变化对压缩模量的影响。梅国雄等[13]将e-p曲线和e-lgp曲线的函数关系应用到土体压缩模量求解中，建立了压缩模量与应力之间的函数关系式，然而该函数关系式为需要进行分段考虑，不便于实际应用。郑俊杰等[14]将参变量最小势能原理引入莫尔-库伦屈服准则中，建立弹性状态下、塑性状态下土体变形模量与压缩模量之间的换算关系，通过该关系式计算得到的压缩模量仍为一个常数。周翠英等[15]对试验结果拟合分析，给出不同状态下淤泥质土在外荷载作用下的压缩模量随压力变化关系。陈福江等[16]对现场采集到的试验数据和实测结果对比分析，给出反应深度变化的土体压缩模量计算方法，由于试验数据缺乏，尚需进一步的深入研究。

以上诸多研究表明天然地基沉降计算中考虑土体的非线性压缩特性已经取得诸多进展。但目前对于散体材料桩复合地基的沉降计算中还鲜见考虑土体非线性压缩特性的计算方法。本文利用经典e-lgσ′（e为孔隙比，σ′为有效应力）非线性压缩关系，建立土体压缩模量Es随有效应力的变化关系，然后基于考虑非线性压缩特性的压缩模量表达式对规范中的应力修正法和复合模量法进行改进，并通过分层总和法完成散体材料桩复合地基的沉降计算。

1 土体的非线性压缩特性

侧限条件下土体压缩特性可通过孔隙比e和有效应力σ′关系曲线描述，如图1所示。取曲线上任意两点连成直线的斜率作为土在侧限条件下的压缩系数a，表达式为[17]：

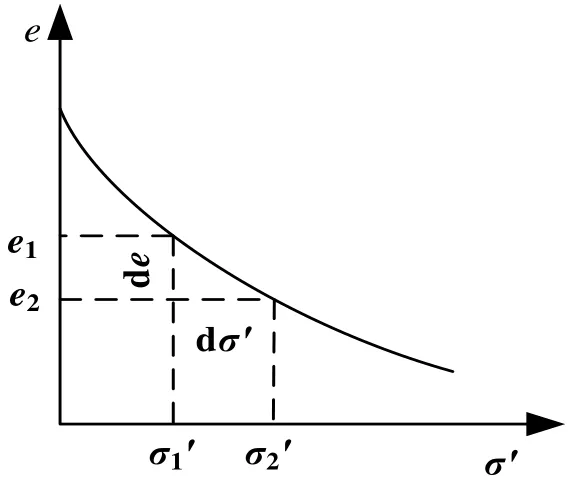
图1 e-σ′坐标系中土的压缩曲线Fig.1 Compression curve of soil ine-σ′coordinate system

式中：e1为e-σ′曲线与有效应力σ1′对应的孔隙比；e2为e-σ′曲线与有效应力σ2′对应的孔隙比。

由图1可知土体的压缩系数a随有效应力σ′增加而减小，有效应力σ′越大，曲线的割线斜率越小，进一步反映出土体压缩性变小。为进一步说明这种压缩特性，将e-σ′关系曲线转换为σ′−ε关系曲线。某级有效应力下的侧限压缩模量Es等于σ′−ε曲线在该点的斜率，可表达为[17]：

根据式（1）和式（2）并考虑dε=de/(1+e0)，可得土体压缩模量与压缩系数之间的关系为[17]：

式中：a为压缩系数；e0为初始孔隙比。

事实上，诸多试验结果[18-21]表明e-σ′关系曲线在e-lgσ′坐标系中将呈现为直线，如图2所示：

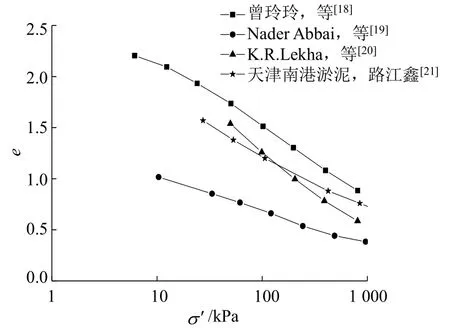
图2 e-lgσ′曲线Fig.2 e-lgσ′curves

天然地基往往成层分布，每层土体的非线性关系可表达为：

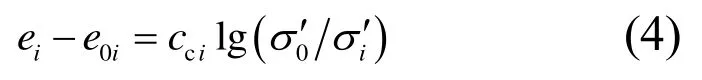
式中：ei为第i层土的孔隙比；e0i为第i层土e-lgσ′曲线与σ0′相对应的初始孔隙比；cci为第i层土的压缩指数；σ0′为初始有效应力；σi′为第i层土的有效应力。

式（4）中由e对σ′求偏导可得：

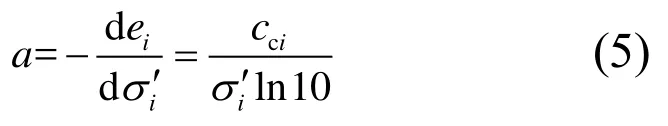
将式（5）代入式（3），得到第i层土压缩模量Esi与第i层土有效应力σi′之间关系为：

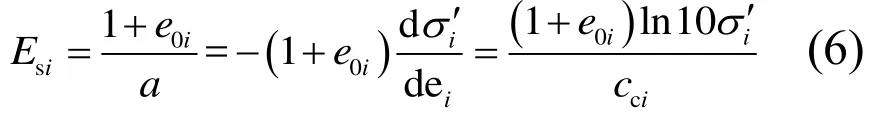
式（6）为考虑非线性压缩特性的土体压缩模量Esi的表达式，从该表达式可以明显看出有效应力的改变会导致土体压缩模量也发生改变，更加真实反映土体的非线性压缩特性。

2 考虑土体非线性的应力修正法

规范中给出的应力修正法只考虑桩间土体的压缩变形，采用土体压缩模量按照分层总和法完成沉降计算。

规范中复合地基的总沉降S可应用应力修正法[4]按照下式开展计算：

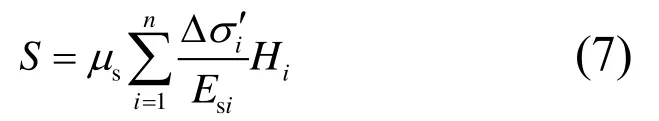
式中：μs为应力修正系数，为第i层复合土层上附加应力增量，；Esi为基础底部第i层桩间土的压缩模量；Hi为第i层复合土层的厚度；n为桩土应力比；m为面积置换率。

式（7）在计算过程中将桩间土体的压缩模量当作常数，这势必对计算结果带来偏差。因此，为了更好反映有效应力与压缩模量之间的非线性关系，对规范中应力修正法中的土体压缩模量按照公式（6）做相应改进，应用改进后的应力修正法并通过分层总和进行复合地基沉降计算的表达式为：

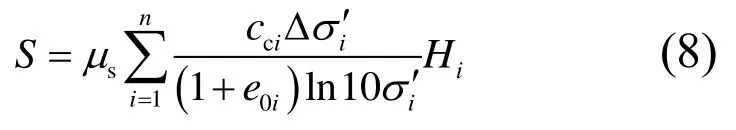
3 考虑非线性特性的复合模量法

相较于应力修正法，规范中的复合模量法同时考虑桩体、桩周土体的压缩变形。其计算过程中对桩体压缩模量、桩周土体压缩模量按照一定比例确定出每层土体的复合模量，再利用得到的复合模量并结合分层总和法完成复合地基的沉降计算。

规范中应用复合模量法开展复合地基沉降计算的公式为[4]：

式中：S为复合地基的总沉降；Δσi′为第i层土的附加应力；Espi为第i层复合土层的复合模量；Hi为第i层土的厚度。

复合地基复合土层压缩模量Espi可通过桩体置换率计算得到，表达式为：

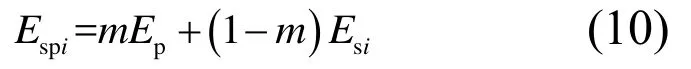
式中：Ep为桩体的压缩模量；Esi为第i层土体的压缩模量；m为桩体置换率。

从式（10）可看出复合模量Espi仅与3个参数有关，并不能反映土体所具有的典型非线性压缩特性，也无法反映复合模量随有效应力变化而发生的真实改变。

由式（6）并结合式（10），给出考虑置换率m、有效应力σi′等影响的复合模量Espi表达式：

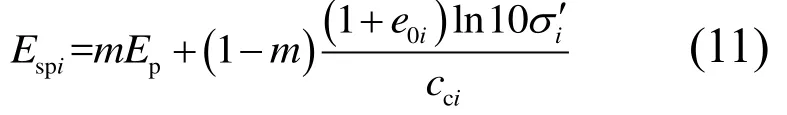
对公式（11）拟合分析，给出置换率分别为0.125、0.25、0.5时复合模量与有效应力间的变化关系，如图3所示：

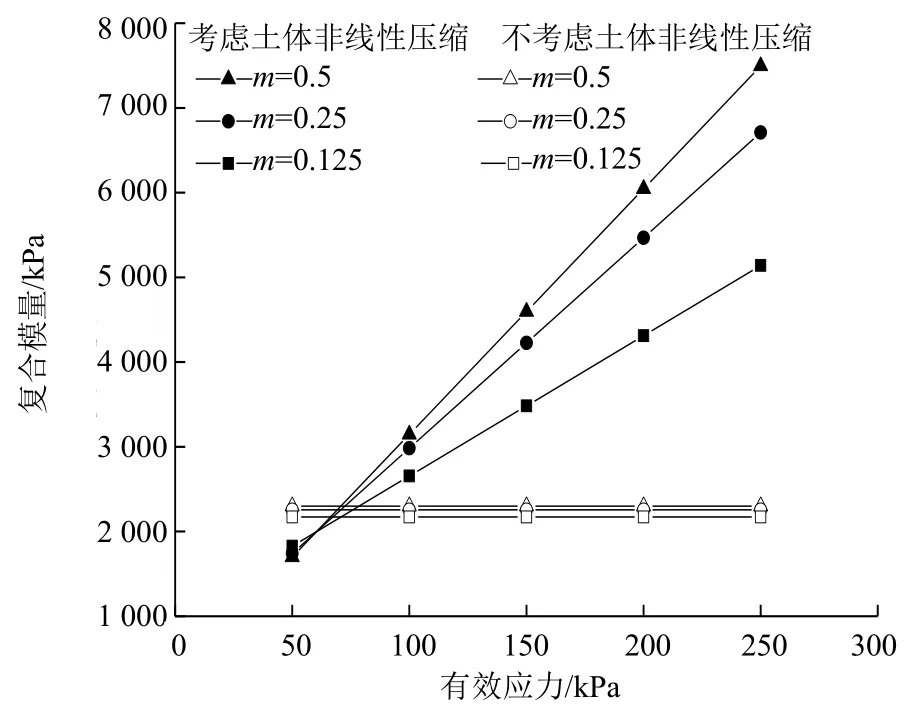
图3 有效应力与复合模量的变化关系Fig.3 Relationship between effective stress and composite modulus

从图3可以明显看出考虑土体非线性压缩特性对复合模量的取值有很大影响，而规范中给出的计算复合模量方法没有考虑土体非线性压缩特性，通过该方法得到的复合模量始终是一个定值。

最后将式（11）代入式（9），得到考虑土体非线性压缩特性的复合模量法通过分层总和计算沉降的表达式为：

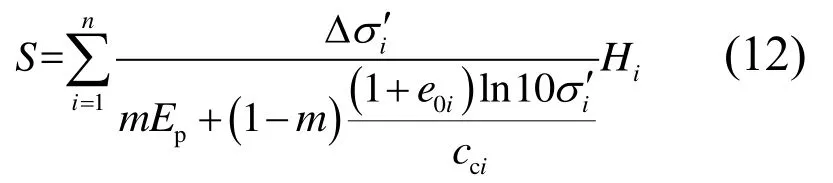
4 案例计算

4.1 室内模型试验

采用文献[22]中模型试验进一步验证本文所提出的计算方法。对传统砂桩复合地基开展分级静力加载试验，砂桩桩长600 mm，桩体直径89 mm，置换率m=8.8%，桩体压缩模量Ep=21 MPa，试验土体为软黏土，液限含水率 42.76%，塑性含水率21.61%，不排水抗剪强度cu=22.25 kPa，压缩指数cc=2.528，初始孔隙比e0=2，土体压缩模量Es=0.73 MPa，黏聚力cs=6.04，摩擦角φs=7.1°。由于模型试验给出的数据不完整，故只对考虑土体非线性压缩特性的复合模量法与规范中的复合模量法及试验值对比分析，结果如图4所示。

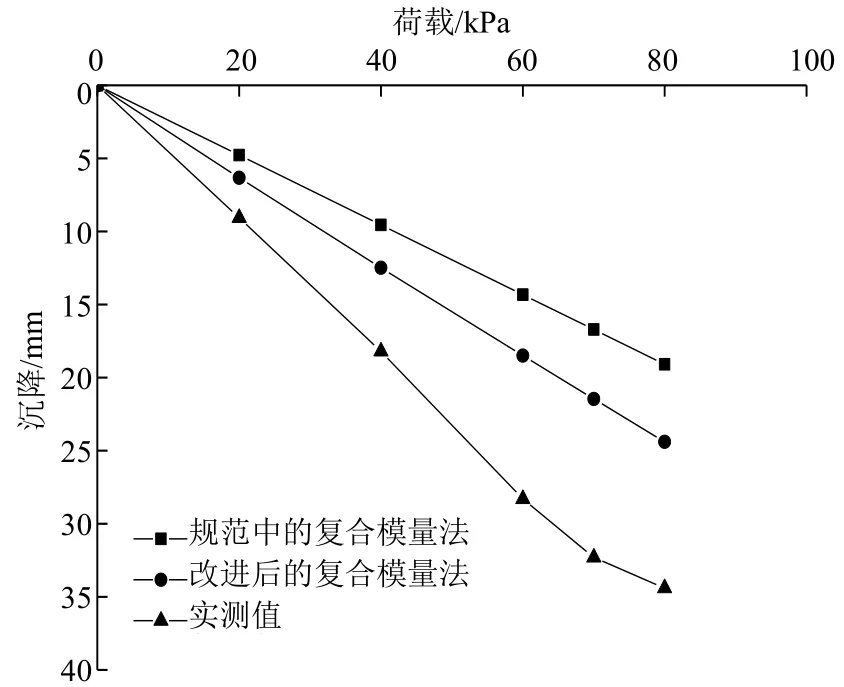
图4 静载试验荷载-沉降关系曲线Fig.4 Load-settlement relation curves of static load test

由图4可以看出，规范中的复合模量法与试验值偏差大，而考虑土体非线性压缩特性的复合模量法计算结果与试验值接近，进一步表明本文计算方法具有一定的可靠性。

4.2 实际工程案例

采用文献[23]中工程案例来验证本文所提出的计算方法。测试场区是一个堆料场（约0.5 km2），用于存放钢板生产所用的原矿和煤矿。拟采用压实碎石柱来加固地基，减少地基沉降。碎石桩长11 m，直径0.8 m，中心间距2 m，正方形布桩，置换率m=0.125，桩土应力比n=2，桩体压缩模量Ep=2 MPa。上部填土高度5.3 m，地基土层自地面以下分为：①砂层，厚度2 m；②软黏土I，厚度2 m；③软至中硬黏土，厚度3 m；④软黏土III，厚度3 m，其中，砂层当作工作平台，便于施工设备的进入。堆料场下部土层的剖面图如图5所示，各土层计算参数如表1所示。

表1 主要计算参数Table 1 Main calculation parameters

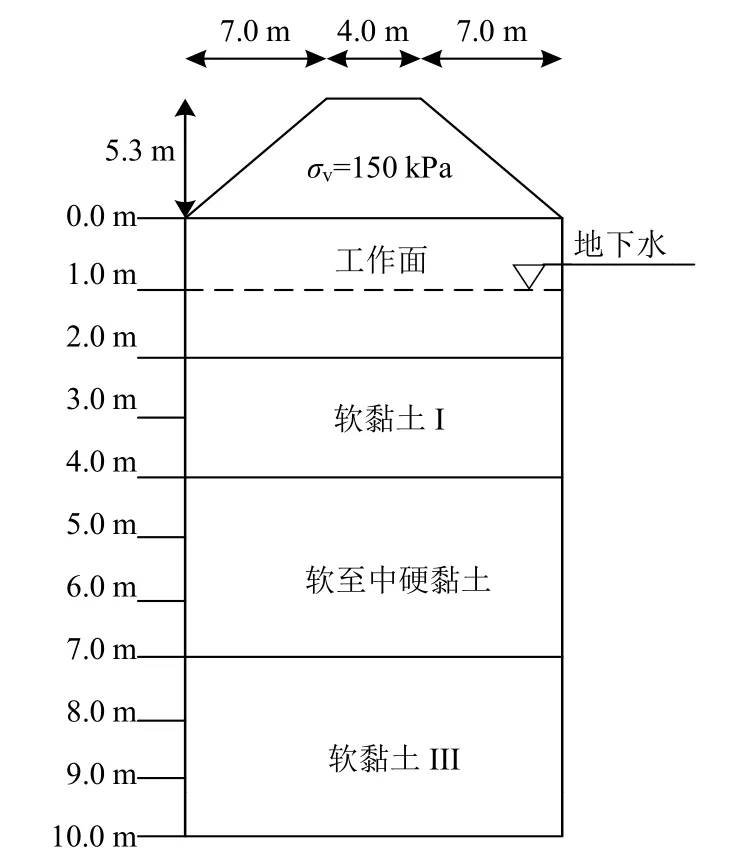
图5 土层剖面图Fig.5 Soil layer profile

采用以上方法计算散体材料桩复合地基的沉降并与规范中给出的方法进行对比，结果如表2所示。

表2 复合地基沉降计算结果的比较Table 2 Comparison of settlement calculation results of composite foundation

由表2计算结果可知，采用规范中的复合模量法得到的计算结果与工程实测值偏差最大，偏差可达到171.06 mm，偏差率达到33.16%，而改进后的应力修正法与实测值偏差4.86 mm，偏差率0.94%，改进后的复合模量法与实测值偏差22.78 mm，偏差率4.42%。产生以上差异的原因是规范给出的散体材料桩复合地基沉降计算方法未考虑土体非线性压缩特性。此外，由前文论述可知，土体的侧限压缩模量与有效应力存在函数关系，即随着土层深度增加，有效应力在不断变化，土体压缩模量不再是一个常数。本文提出的改进计算方法，较好的考虑这一变化特点，因而更接近实际情况。