动三轴试验确定土样动强度指标中的两个问题
2021-11-10陈龙珠顾晓强
陈龙珠,顾晓强
(1.上海交通大学 船建学院土木工程系,上海 200240;2.同济大学 土木工程学院地下建筑与工程系,上海 200092)
0 引 言
土质地基、边坡及工程建(构)筑物,在地震和其它动荷载作用下的动力反应分析和安全评估,需要土的动力特性及其力学模型,其中包括土的动变形和动强度等方面的特性参数。土在动力作用下的特性,与土的类型、初始物理和力学状态、约束条件以及动力作用特性等内外因素密切相关。在实验室内测试地基土动力性质的方法有很多种,包括动三轴、动单剪、动扭剪、共振柱和超声波速测试等方法。由于在测试时试样的初始力学状态、约束条件和施加的动荷载形式及其强弱有所不同,这些方法各有其适用范围和优缺点,其中动三轴试验目前应用得最为广泛,我国国家标准《地基动力特性测试规范》(GB/T 50269—2015)[1]、《土工试验方法标准》(GB/T 50123—2019)[2]等先后已涵盖了这个方法。
动三轴试验早期主要用于土在地震作用下的动力特性,包括土的动模量、阻尼比以及动强度和液化指标等。地震作用具有不规则性,但在动三轴试验中,通常将其等效成周期荷载施加到试样之上。如图1所示,类似于常见的静三轴试验,动三轴试验的试样也是一个圆柱体,装入压力室内,先施加侧向应力σ3c和轴向应力σ1c进行静力固结(定义固结应力比为Kc=σ1c/σ3c),然后再施加轴向的周期应力 σd=σd0sin(ωt),其中σd0为动应力幅,ω=2πf为圆频率(f为频率),t为时间。在动应力作用过程中,量测试样的动应力、动应变和孔隙水压力变化的时程曲线,然后对此根据采用的破坏标准,确定在这种动应力幅下的破坏振次Nf等参数。

图1 动三轴试验试样的受力状态[3]Fig.1 Stress state of dynamic triaxial test specimen[3]
为确定试样的动强度,目前可供选用的常见破坏准则有三种:(1)试样轴向应变幅增大到一定的限值(应变标准);(2)饱和砂土试样的超静孔隙水压力升高到了初始静力固结围压而出现液化(孔压标准);(3)试样应力状态达到了极限平衡条件(极限平衡标准)。《地基动力特性测试规范》(GB/T 50269—2015)规定,试样动强度的破坏标准,可在动应变幅2.5%~10.0%范围内确定,而对可液化土则可采用初始液化或2.5%的动应变幅。
当试样振动达到破坏标准时,其 45°面上的动强度比Rf由下式计算:

式中:σc为试样平均固结应力,二维问题时取σc=(σ1c+σ3c)/2,三维问题时取σc=(σ1c+2σ3c)/3。也有用σ3c替代式(1)中的σc,相对更便于应用。
对固结应力比Kc和所用破坏标准相同的一组试样,可绘制Rf-Nf关系曲线(如图2),它实际上是对土的动强度采用固结应力进行归一化处理,其中横坐标通常选用对数。应用时,根据工程要求的固结应力比和等效破坏振次Neq,在该曲线上确定相应的动强度比Rff。
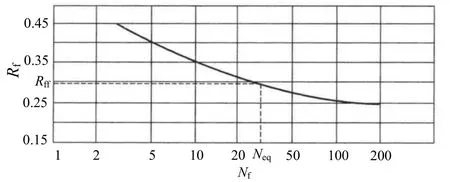
图2 动强度比与破坏振次的关系曲线示意图[3]Fig.2 Schematic diagram of relation between dynamic strength ratio and number of cycles to failure[3]
在进行地基整体动力稳定分析时,需要用到土的固结不排水动强度指标cd(动凝聚力)和φd(动摩擦角)。文献[2]、[5]这两本国内和国际试验标准未包含与此相关的条款,而文献[1]、[3]和[4]说明的确定方法基本相同:对密度、破坏准则类型、固结应力比相同但固结应力不同的一组试样,由Rff和固结应力确定破坏时的动应力幅,将其与固结应力σ1c叠加,再由此绘制一组应力圆(如图 3),其公共切线就是土的动强度包线:
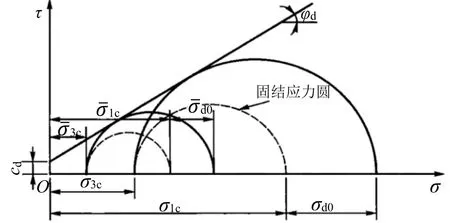
图3 受压试样动强度的总应力圆分析[4]Fig.3 Total stress circle analysis for dynamic strength of specimens under compression[4]

式中:τf是土的动抗剪强度;σf为潜在破坏面上的法向应力。
针对文献[1]、[3]和[4]说明的动三轴试验确定试样动强度指标的方法,经研读后,发现有两个问题值得讨论和作出澄清。本文对此抛砖引玉,欢迎同行专家指正。
1 动强度比与破坏振次关系曲线的归一化问题
按上述求土的动强度指标的做法,对图3所示的两个应力圆,一般来说φd≠0,根据几何关系分别可得:
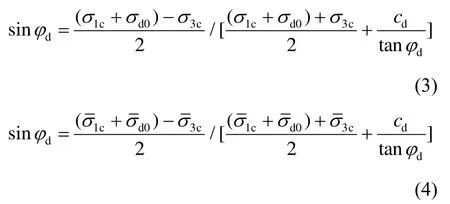
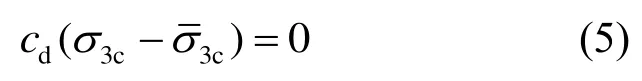

该式表明,动摩擦角φd会随着固结应力比Kc的增大而有所增大,但会随着动强度比的减小或破坏振次的增大而有所减小。
对黏性土来说,一般cd≠0。从上述推导来看,即使是具有相同的固结应力比和破坏振次,对σ3c不同的一组黏性土试样,其相应的动强度比Rff将会彼此有所不同。也就是说,对图3中的两个破坏应力圆,σd0=2Rffσ3c,,否则将不能得到cd≠0的计算结果。由此可作进一步推论,对黏性土,由于cd≠0,将不能像无黏性土那样,去谋求获得如图3所示的比较理想的归一化曲线。
2 试样动力破坏类型的判别问题
对无黏性土,cd=0,在求其动摩擦角φd时,当固结应力比Kc较小时,涉及到破坏时的动应力幅σd0,是与轴向固结应力σ1c相加(动力压缩)还是相减(动力拉伸)的选择问题。如同现有的书刊,本文上面的分析,隐含着是将两者相加的。对轴向周期荷载σd来说,在每个周期(振次)里,半个周期与σ1c同向,半个周期则与σ1c反向:当固结应力比Kc较小时,就会出现0<σ1c−σd0<σ3c的情况。以等向固结为例,Kc=1.0,若认为试样是在动力压缩半周期内达到破坏,则sinφd1=σd0/(2σ3c+σd0)=Rff/(1+Rff),但若认为试样是动力拉伸半周期内达到破坏,则sinφd2=σd0/(2σ3c−σd0)=Rff/(1−Rff)。显然,在Rff/(1−Rff)<1条件下,φd2>φd1。可见,认为试样是动力受压破坏而得出的动摩擦角数值偏小,对地基土的整体稳定分析结果将偏于保守。
在周期荷载作用下,假设试样在受压和受拉半周期内到达的潜在破坏面对应于同一条强度包线,则对于任意的固结应力比Kc,由应力圆图上的几何关系得:
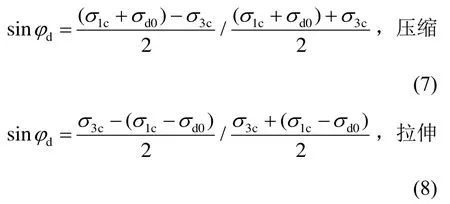
将两式联立求解,则可以得到试样在压缩和拉伸两个相邻的半周期内均到达强度包线时的临界动应力幅:
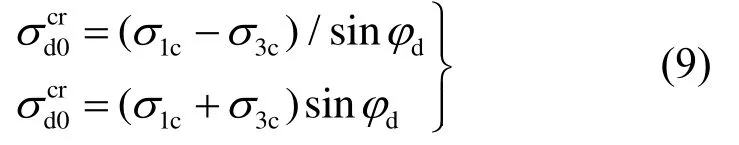
上式第一个公式的右边,与《地基动力特性测试规范》(GB/T 50269—2015)[1]中的第9.4.9条所列算式形式相同。
由于动摩擦角是待求的无黏性土的动强度指标,上面两种形式的算式均不便于应用。因此,将两式两边分别相乘,得到一个与动摩擦角无关的新算式:
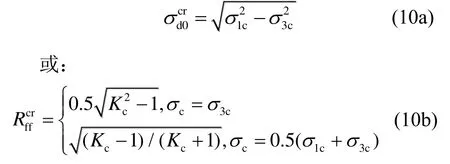
由实测试样破坏时的动应力幅或动强度比和式(10),可以判断出试样破坏的类型:

再看等向固结(Kc=1.0)的无黏性土试样,由式(10b)容易得到。因此,应对其以拉伸破坏对应的计算公式来确定动摩擦角:由式(11),当取σc=σ3c时,sinφd=Rff/(1−Rff),与上一节推导的相应结果一致。
