前、后轴双电动机驱动纯电动客车的转矩分配策略

吴迪瑞， 田韶鹏

(1. 武汉理工大学 现代汽车零部件技术湖北省重点实验室， 湖北 武汉 430070； 2. 武汉理工大学 汽车零部件技术湖北省协同创新中心， 湖北 武汉 430070； 3. 武汉理工大学 湖北省新能源与智能网联车工程技术研究中心， 湖北 武汉 430070)

前、后轴双电动机驱动纯电动客车的动力系统构型特点在于前轴和后轴上各有1个驱动电动机独立输出驱动力，即双电动机双轴驱动系统是一种过驱动系统.转矩分配的灵活性使转矩分配策略成为了轮毂电动机驱动电动汽车(foul-wheel-driven electric vehicle,4WD EV)和前、后轴双电动机驱动电动汽车(front-and-rear-wheel-independent-drive-type electric vehicle,FRID EV)的研究热点.当前研究的转矩分配策略按其设计目标主要分为2种： ① 基于车辆经济性的转矩分配策略；② 基于车辆稳定性的转矩分配策略.

基于车辆经济性的转矩分配策略按其研究方法主要分为2种： ① 基于电动机效率特性，以电动机台架试验得到的电动机效率MAP图为依据，优化前、后轴电动机转矩分配系数，选择综合效率最高的转矩分配方案；② 基于电动机控制原理，建立电动机损耗模型，推导最优转矩分配策略.熊会元等[1]基于电动机的MAP特性，提出双电动机利用效率为控制目标的转矩优化分配策略，并在3种驱动模式下，与双电动机平分转矩策略进行对比仿真.姜涛等[2]提出以前、后电动机总功率损失为目标函数的转矩优化分配模型，仿真结果表明，转矩优化分配策略不仅能减少驱动工况的功率损失，还能增加制动工况下的能量回收.李胜琴等[3]在多种典型循环工况下将最优转矩控制策略与双电动机平均分配和Cruise默认控制策略2种控制方式进行了比较分析，证明了最优控制策略的普遍合理性.

基于车辆稳定性的转矩分配策略主要分为2种： ① 针对纵向稳定性的滑移率控制策略，又称驱动防滑策略；② 针对横向稳定性的横摆力矩控制策略.由于横摆力矩控制只能在轮毂电动机驱动电动汽车上实现，而且研究对象不同，本文不深入研究.N. MUTOH等[4-5]以前、后轴双电动机驱动纯电动汽车为研究对象，提出了基于车轮滑动率的驱动控制策略.此外，可采取分层控制的方式，综合不同的转矩分配策略，以提高控制策略的性能.黄开启等[6]针对分布式驱动电动汽车提出一种以轮胎利用率和纵向驱动力为目标函数，基于广义横摆力矩决策控制的转矩分配策略.该策略同时保证了车辆的横向稳定性和纵向稳定性.续丹等[7]以质心侧偏角作为考察稳定性的指标，用模糊控制方法，所建立的系统能效函数综合了基于稳定性和基于经济性的转矩分配结果.以系统能效函数为基础的转矩分配策略既能保证车体稳定行驶也有一定的节能效果.LIN C.等[8]针对四轮驱动电动汽车提出了基于罚函数法的分层转矩分配策略，惩罚函数包括了滑移率约束、横摆力矩补偿控制和动力系统能耗，基于简化的罚函数进行离线优化，并根据滑移率约束在对应的离线结果附近通过在线优化方法取得局部极小值.A. M. DIZQAH等[9]提出一种在横摆力矩控制下，用查表法实现最优转矩分配策略.ZHAO Y. Q. 等[10]分别建立了基于模糊算法的稳定性控制策略和基于电动机损耗模型的经济性控制策略，并通过判断分布式驱动电动汽车是否处于稳定状态来决定采用哪种控制策略分配电动机转矩.

综合考虑以上各转矩分配策略的出发点和控制目标，笔者提出综合考虑车辆经济性和车辆稳定性的综合转矩分配策略，该策略分为基于电动机效率特性的最优转矩分配和驱动防滑策略2部分.利用Cruise软件和Matlab上的Simulink模块建立联合仿真模型对综合转矩分配策略的优化效果进行分析，验证综合转矩分配策略的合理性.

1 双电动机驱动纯电动客车结构

前、后轴双电动机驱动纯电动客车的动力传动系统结构如图1所示，汽车的动力由2个电动机分别经过前轴和后轴减速器到达前轴左右车轮和后轴左右车轮.前、后轴的动力由前、后轴电动机独立提供，而前、后轴电动机的输出转矩可由前、后轴电动机控制器实时控制，使总需求转矩可以被实时分配到前、后轴驱动电动机上.

图1 纯电动客车动力传动系统结构图

2 综合转矩分配策略总体架构

前、后轴双电动机驱动纯电动客车具有双电动机双轴驱动的动力系统构型，前、后轴由各自的电动机独立输出驱动力，需要设计转矩分配策略进行前、后轴电动机转矩指令的分配，因此转矩分配系数成为了转矩分配控制策略的控制变量.而基于车辆稳定性的转矩分配策略的控制结果是对前轴和后轴驱动电动机的转矩输出进行限制，并没有确定地给出转矩分配系数，这使得综合考虑稳定性和经济性的转矩分配策略成为可能.综合上述2种转矩分配策略，提出以滑移率控制为约束、提高电动机综合效率为目标的综合转矩分配策略，该策略示意图如图2所示.

图2 综合转矩分配策略示意图

3 驱动防滑转矩控制策略

纯电动客车的动力性主要由驱动电动机所确定的驱动力决定.但是当在潮湿或冰雪路面附着性能差时，由于附着力有限，地面的切向反作用力低于驱动力，过大的驱动力可能引起车轮的过度滑转.为防止滑转的出现影响整车动力性能和操纵稳定性，当车轮滑移率升高时，有必要通过限制驱动电动机的转矩来限制驱动力，达到控制车轮滑移率的目的，提升整车稳定性.

驱动防滑控制策略的主要运行流程如下：① 分别计算前轴和后轴的左右共计4个车轮的滑移率slf、srf、slr、srr；② 根据高选原则确定前轴和后轴的采样滑移率；③ 将前轴和后轴的采样滑移率分别与逻辑门限值0.2做比较，若采样滑移率大于逻辑门限值0.2，则判定该轴左右车轮发生了滑转并进入步骤④，否则判定该轴左右车轮未发生滑转并进入步骤⑤；④ 将该轴滑移率与逻辑门限值0.2的差值作为PID控制器的输入，输出为该轴的转矩指令限值；⑤ 计算该轴上驱动电动机当前电动机转速对应的峰值转矩，作为转矩指令限值输出.

根据车速传感器和轮速传感器的信号，计算各个车轮滑移率，计算公式为

(1)

式中：s为车轮滑移率；rd为车轮滚动半径；ω为车轮角速度，从轮速传感器获得；v为车辆行驶速度，从车速传感器获得.

将传感器参数代入式(1)得左前、右前、左后和右后的车轮滑移率分别为slf、srf、slr、srr.由于同轴上的左右车轮都由同一驱动电动机驱动，左右车轮不能单独控制，所以需要采用高选原则，以左右车轮中车轮滑移率较大的作为电动机转矩修正依据，可得到前轴滑移率sf和后轴滑移率sr.典型的车轮滑移率与路面附着系数φb的特性曲线[11]如图3所示.

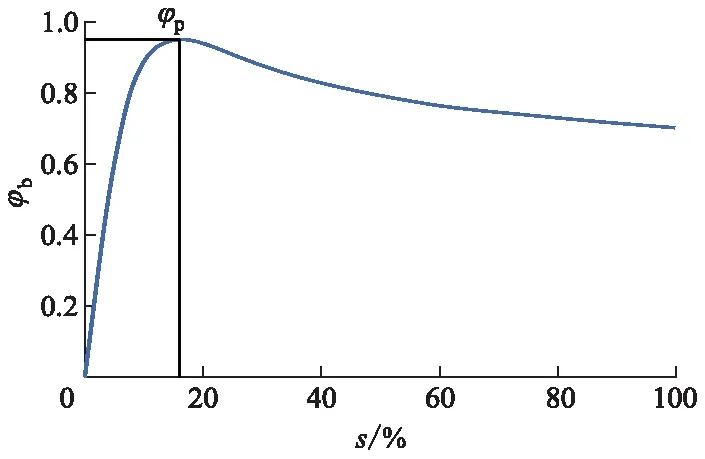
图3 车轮滑移率与路面附着系数的特性曲线

设峰值附着系数φp对应的滑转率为车轮最佳滑移率s0.从图3可以看出：当s≤s0时,附着系数随车轮滑移率增加而增大,当车轮滑移率在此范围时，若驱动力大于附着力导致车轮滑移率增加，由于φb会随车轮滑移率增加单调增大，附着力随之增大，反而抑制车轮滑移率的增加，即车轮滑移率与附着力为负反馈系统，车辆运行状态稳定.

当s>s0时，附着系数随车轮滑移率增加而减小，车轮滑移率与附着力为正反馈，若驱动力不变，车轮滑移率会随时间推移持续增大直到车轮打滑，此时车辆运行状态不稳定.

s0在15%到20%之间，此区间纵向附着系数最大驱动力可得到发挥，为保证动力性，取车轮滑移率20%为驱动防滑控制策略介入转矩控制的逻辑门限值.

当前轴/后轴的采样滑移率(sf/sr)大于逻辑门限值20%时，对转矩的调节通过PID控制实现，在前一时刻前轴/后轴转矩指令(Tf/Tr)上减去修正量(ΔTf/ΔTr)可得前轴/后轴电动机转矩指令限值(Tfs/Trs).

前轴转矩指令修正量为

(2)

式中：kp为比例系数；TI为积分时间常数；TD为微分时间常数.

前轴电动机转矩指令限值为

Tfs=Tf+ΔTf.

(3)

后轴电动机转矩指令限值Trs的计算方法同上.

当sf/sr小于逻辑门限值20%时，将前轴/后轴当前电动机转速下峰值功率对应转矩(Tfmax/Trmax)作为电动机转矩指令限值(Tfs/Trs).

4 转矩最优分配策略

不同于单一的基于效率最优的转矩分配策略，由图2可知，转矩最优分配策略的输入除驾驶员期望转矩外，还有前轴/后轴电动机转矩指令限值.因此，除驾驶员期望转矩与车速信号外，将前轴/后轴电动机转矩指令限值也作为输入，对转矩分配系数进行在线寻优.

4.1 转矩最优分配策略的合理性论证

基于效率最优的转矩分配策略通过合理分配前、后电动机的转矩指令，提高前、后电动机的综合效率，从而减少前、后电动机的总输入功率，节省能量，提高整车的经济性.该控制策略通过分配前、后电动机的转矩指令，就是在相同的总需求转矩下，改变前、后电动机的转矩比例，减小前、后电动机的损失功率之和.研究对象的前、后电动机型号相同，转速为3 000 r·min-1时，电动机损失功率Ploss随电动机总输出转矩Td的变化曲线如图4所示.

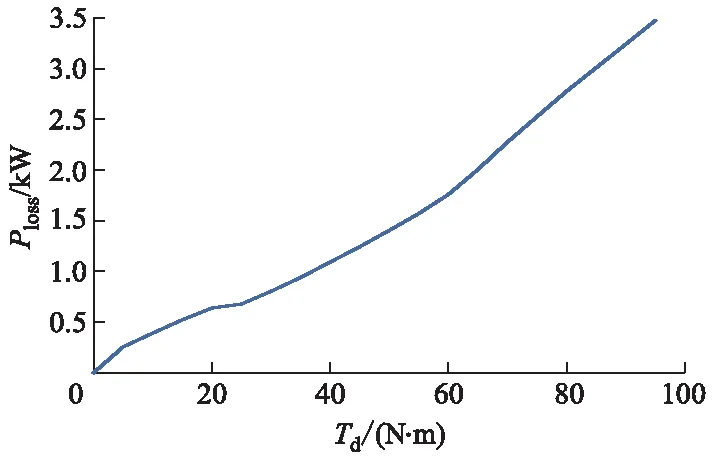
图4 电动机损失功率随电动机总输出转矩的变化曲线

转矩分配系数为

(4)

驱动电动机总输出转矩为

Td=Tf+Tr.

(5)

假设效率最优的转矩分配策略是转矩平均分配，则对于任意的Td和dmt，恒有

(6)

式(5)符合凹函数的定义，所以Ploss与电动机转矩的函数曲线为凹函数.这与图4的电动机功率损失函数曲线相矛盾，所以转矩的最优分配方法并不是转矩平均分配.

以上证明过程表明对于研究对象而言，转矩平均分配并不是最优转矩分配方法.通过合理分配前、后电动机转矩指令来提高整车经济性的转矩最优分配策略相比转矩平均分配具有节能潜力.

4.2 转矩最优分配策略数学模型

4.2.1目标函数

为了使整车经济性最大化，采用基于效率最优的转矩分配策略来分配前轴与后轴驱动电动机的转矩分配.可转化为前轴与后轴驱动电动机转矩分配系数的确定和总输出转矩的确定.

由电动机的效率特性可知，电动机转矩与电动机效率为非线性关系，转矩最优分配策略的目标在于寻找最优的驱动电动机综合效率.问题实际上是一个非线性函数极值寻优问题，对于类似问题往往使用智能算法求解.优化问题可表述为在任一工况点下，寻找dmt，使驱动电动机综合效率ηm为最高.由Tf=dmtTd、Tr=(1-dmt)Td得

(7)

式中：n为车速对应的电动机转速；η(Tf,n)为前轴驱动电动机转矩为Tf、转速为n时的效率；η(Tr,n)为后轴驱动电动机在转矩为Tr、转速为n时的效率.

目标函数为

maxηm(dmt).

(8)

4.2.2约束条件

为了提高整车经济性，采用基于效率最优的转矩分配策略来分配前轴与后轴驱动电动机的转矩.根据dmt和Td的定义，转矩分配问题可转化为dmt和Td的确定问题.

此外，将Tfs/Trs作为动态约束条件，确定dmt与Td的取值范围，当Tfs+Trs大于总需求转矩Treq时，Tfs/Trs决定Tf与Tr的取值范围：

(9)

对于dmt与总输出转矩,有

(10)

综合上述分析，该优化问题的约束条件为

(11)

4.3 粒子群优化算法

选用粒子群算法作为转矩分配优化问题的优化算法.由于优化问题的相关变量包括Treq、n、Tfs和Trs共4个变量，若采用离线优化与查表法结合的方式，所有工况的总数据量较大，占用内存大，故选用实时优化的方法，仅需要将三次曲线拟合得到的驱动电动机MAP图存为数组，在粒子群算法进行适应度函数运算时调用，减少内存的占用.

4.3.1公式更新

由于工况点有Treq、n、Tfs和Trs共4个维度，复杂多变的工况使计算时间大大增加，考虑到这一点，提出基于粒子群算法的最优转矩分配策略.

2) 迭代过程中的位置和速度更新.在进行迭代时，先计算个体和全局的历史最优解，然后进行个体位置和速度的更新，更新公式为

(12)

4.3.2算法流程

5 仿真结果分析

通过Cruise调用Simulink控制策略模型使用代码生成技术转换为C语言，再由编译器生成的DLL文件格式，实现AVL-Cruise与Simulink联合仿真.为验证综合转矩分配策略的合理性，在AVL-Cruise平台上搭建经济性仿真模型，在Matlab/Simulink平台上搭建包含了综合转矩分配策略的整车控制策略模型.仿真模型的相关参数包括整车参数、动力部件性能参数及驱动电动机效率MAP图.整车参数如下：整车整备质量为1 800 kg；整车满载质量为2 500 kg；迎风面积为5 m2；机械传动系统效率为0.95；风阻系数为0.4；滚动阻力系数为0.01；轮胎滚动半径为291.5 mm.动力传动系参数如下：电动机额定功率为19 kW；电动机峰值功率为30 kW；电动机峰值转速为7 500 r·min-1；电动机峰值转矩为110 N·m；电动机额定电压为115 V；电动机额定电流为165 A；主减速器传动比为6.7.动力电池参数如下：电池类型为磷酸铁锂；单体电池电压范围为2.50～3.65 V；单体电池个数为100个；电池包额定电压为320 V；总容量为135 A·h；成组方式为100S1P；SOC(state of charge)工作范围为5%～100%.

使用Matlab软件的三次多项式拟合函数处理电动机台架试验数据，得到的驱动电动机效率η的MAP拟合结果如图5所示.

图5 驱动电动机效率的MAP拟合结果图

5.1 离线转矩最优分配策略仿真

单一转矩最优分配策略运行时常采用离线优化，仿真结果如图6所示.

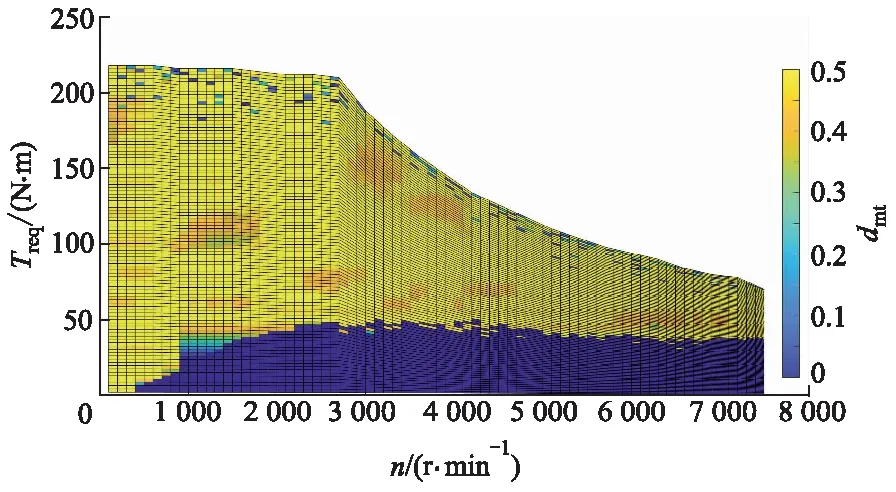
图6 离线优化转矩分配系数MAP图

离线优化的转矩最优分配策略仿真结果可以验证转矩最优分配策略模型的正确性，由图6可以看出，前/后轴的转矩分配主要受需求转矩影响，电动机转速在900 r·min-1到峰值转速的区间内，当需求电动机转矩低于40 N·m时，需求电动机转矩过小，为避免驱动电动机运行在低转矩输出的低效率区域，dmt为0；当需求电动机转矩高于40 N·m时，需求电动机转矩较大，为避免驱动电动机运行在高转矩输出的低效率区域，转矩分配系数dmt几乎都在(0.3，0.5)内，转矩倾向于平均分配，使驱动电动机尽可能运行在高效率区域.

5.2 NEDC循环工况转矩分配结果分析

为验证综合转矩分配策略对整车经济性的积极作用,使用Cruise-Matlab联合仿真平台分别运行限制了最高车速为100 km·h-1的欧洲市郊工况NEDC_100、限制了最高车速为100 km·h-1全球轻型车统一测试循环工况WLTP_100和纯电动汽车测试经济性常用的等速60 km·h-1循环工况，并对比优化前的转矩平均分配策略整车模型与优化后的综合转矩分配策略整车模型的经济性仿真结果.

结合驱动电动机工况点的分布和转矩分配系数离线优化结果可以直观地体现循环工况中电动机转矩的分配状况.模式1与NEDC_100工况下，转矩平均分配策略和综合转矩分配策略驱动电动机工况点分布如图7所示.

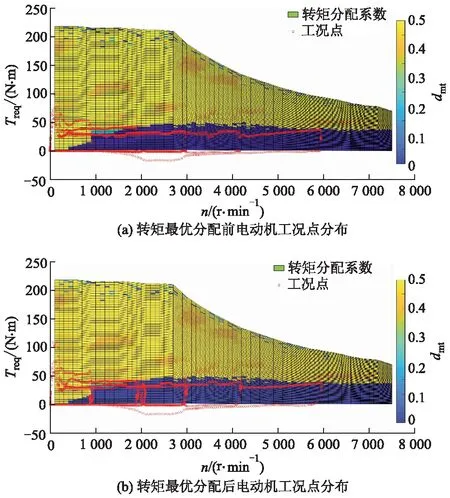
图7 优化前、后驱动电动机工况点分布图

从图7可以看出：离线优化中，转矩分配系数为0.5左右的工况点，优化前后驱动电动机的工况点分布几乎没有变化；在转矩分配系数接近0的工况点，转矩需求被分配给了后轴电动机.总体来讲，工况点的变化符合离线优化结果，说明转矩最优分配策略得到了执行.驱动电动机的综合效率得到了提高，从而提高了动力电池能量的利用效率和整车经济性.

5.3 循环工况下转矩分配策略对比仿真分析

使用综合转矩分配策略进行在线优化， 3种循环工况下优化前后的动力电池SOC变化趋势对比如图8所示.其中t为仿真时间.

图8 3种循环工况下动力电池SOC变化趋势对比

3种循环工况下，100 km电耗的仿真结果如表1所示.

表1 3种循环工况下100 km电耗仿真结果

从表1可以看出：3种工况下，综合转矩分配策略都显著减少100 km电耗，整车经济性显著提高，在WLTP_100工况下，100 km电耗减少了3.33%；3种工况下100 km电耗平均减少了4.79%.

在WLTP_100工况下消耗85%SOC的重复循环工况的续驶里程仿真结果如表2所示.

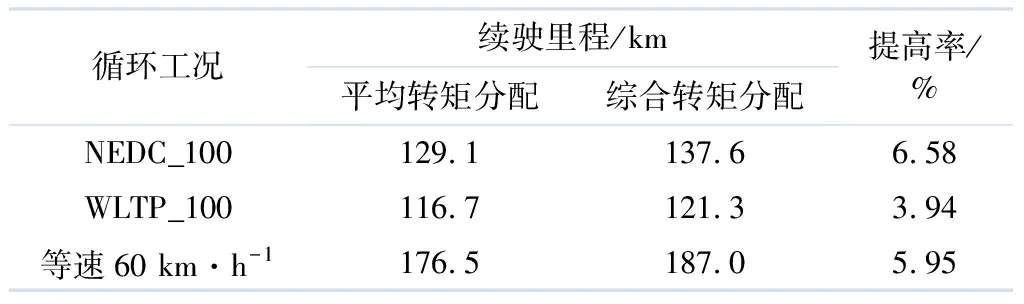
表2 WLTP_100工况消耗85%SOC的续驶里程仿真结果

从表2可以看出：相比平均转矩分配方案，综合转矩分配方案在NEDC_100、WLTP_100和等速60 km·h-1这3种重复循环工况下，续驶里程平均提高了5.49%.

6 结 论

1) 通过对基于经济性的转矩分配策略和基于稳定性的转矩分配策略的分析，提出了一种综合考虑车辆经济性和稳定性的综合转矩分配策略，使用PID进行滑移率控制的驱动防滑策略输出的前、后轴电动机转矩限值，作为基于效率特性的粒子群算法优化的动态约束条件，既避免了车轮打滑，提高了车辆稳定性，又能使最优转矩分配策略在驱动防滑策略生效时仍然能输出最优的转矩分配系数，在保证车辆稳定性的同时提高经济性.

2) 基于整车参数和动力系统关键部件参数，在Cruise-Matlab平台上进行了联合仿真，分析了综合转矩分配策略模型在NEDC工况下的转矩分配情况，相比转矩平均分配策略，3种工况下循环工况仿真结果表明100 km电耗平均减少了4.79%；3种工况下消耗85%SOC的重复循环工况仿真结果表明续驶里程平均提高了5.49%，验证了提出的综合转矩分配策略的合理性.