基于屏障函数的船舶自适应控制
2021-11-10赵向涛于双和
赵向涛, 阎 妍, 于双和, 赵 颖
(大连海事大学 船舶电气工程学院, 辽宁 大连 116026)
近年来,水面船舶已广泛应用于海洋勘探、海上消防与供给等领域.海上船舶除了拥有非线性、大惯性、大时滞等特点,有时候还会受到模型不确定性和复杂环境问题的影响.针对未知的干扰船舶控制问题的研究已经有了很多丰硕的研究成果[1],其中作为一种鲁棒控制器的滑模控制已得到十分广泛的应用[2].文献[3]通过引入纵荡跟踪误差构建一阶滑动变量,引入横漂跟踪误差,构建二阶滑动变量来设计控制律,以实现欠驱动自主水面船舶的轨迹跟踪控制.文献[4]基于滑模控制原理,提出了一种克服状态和控制输入量化效应影响的轨迹控制律.文献[5]针对输入非线性和外部未知扰动,采用基于滑模的自适应控制与非线性扰动观测器相结合的方法,实现水下自主航行器的姿态控制器.文献[6]提出了一种新的非奇异有限时间反步控制器来克服未知扰动对船舶轨迹跟踪控制的影响.通常滑模策略的应用需要预先知道扰动的上界,通过调节滑模增益大于这个上界来保证系统的稳定性.实践中,这一上界通常是未知的,而且由于滑模控制器中的不连续项会导致系统抖振,加剧机械磨损.
考虑到上述因素,为了减少系统抖振和处理不确定扰动上界不可获得的问题,有人提出了自适应滑模控制策略.文献[7]提出了一种具有不确定参数的非线性系统的自适应滑模控制器,通过自适应调节滑模增益来克服不确定参数的影响,设计一个处理系统的抖振的切换函数,并取得了很好的控制效果.但是只是在处理抖振时应用切换函数来减小抖振,自适应增益是个单调递增的函数,容易过分高估干扰上界的问题.文献[8]在不匹配干扰上界未知的情况下,构造辅助输出,然后采用高增益观测器估计所构造的输出,采用自适应律调节滑模增益,保证系统鲁棒性,并且避免抖振.文献[9]针对输入输出约束、不确定干扰和模型不确定问题,提出一种时变非对称李雅普诺夫函数递归自适应滑模控制策略,实现准确跟踪期望轨迹.文献[10]提出一种基于双层递归神经网络的自适应全局滑模控制器,实现动态系统的快速有限时间收敛.文献[11]提出了建立动态自适应控制增益以确保滑模的有限时间收敛,而且设计的自适应律能够避免过分高估不确定性的上界.
近年来,在Brunovsky系统中,文献[12]提出了一种利用屏障函数约束处理的方法来实现自适应滑模控制,屏障李雅普诺夫函数可以保证跟踪性能和约束条件.文献[13]针对二阶扰动,且扰动的界为未知的情况下,提出一种基于屏障函数的螺旋控制器.文献[14]介绍了一种具有未知函数的输出反馈非线性系统的自适应神经网络控制.使用神经网络输出来处理未知函数,通过保证屏障函数的有界性,约束未知函数的参数保持在一个紧凑的超集中,使得神经网络的近似条件成立.基于屏障函数的自适应滑模控制策略的主要优势在于[12]:① 滑动变量可以在有限时间内收敛到预定义的零的邻域,不需要任何干扰的先验信息;② 保证滑模增益不会超过不确定干扰幅值的上界,减小系统抖振.
为此,笔者首次将屏障函数自适应滑模控制的思想引入到船舶轨迹跟踪的控制当中,同经典滑模控制相比,不需要知道干扰的先验信息,在保证系统轨迹跟踪性能的情况下减小系统的抖振,从而减小船舶航行过程中的机械磨损.通过Matlab进行数值仿真,验证控制器的有效性.
1 预备知识
1.1 ASV系统建模
船舶的动态模型可描述为
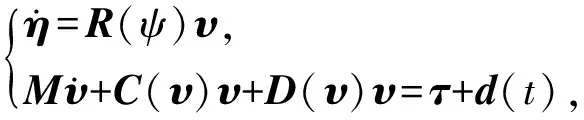
(1)
式中:η=[x,y,ψ]T∈R3,其中(x,y)和ψ分别为大地坐标系下的三自由度位置和航向角;υ为附体坐标系下的速度向量,u、v和r分别为前向速度、横漂速度和偏航角速度,υ=[u,v,r]T∈R3;τ为控制输入向量,τ1、τ2和τ3分别为前进方向控制力矩、横漂方向控制力矩和艏摇方向控制力矩,τ=[τ1,τ2,τ3]T;C(υ)为科里奥利向心力矩阵;D(υ)为非线性水动力阻尼矩阵;d为外部不确定干扰,d=[d1,d2,d3]T,d1和d2分别为作用于横向和纵向上的干扰力,d3为作用在艏摇方向上的干扰力矩.由附体坐标系到惯性坐标系的旋转矩阵R(ψ)定义为
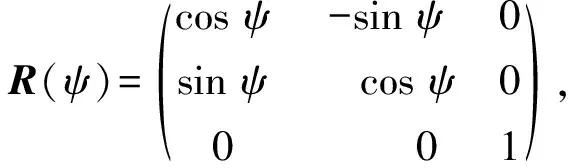
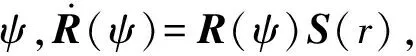

M为质量惯性矩阵,M=MT>0,定义为
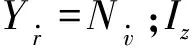

式中:d11=-Xu-X|u|u|u|-Xuuuu2;d22=-Yv-Y|v|v|v|-Y|r|v|r|;d23=-Yr-Y|v|r|v|-Y|r|r|r|;d32=-Nv-N|v|v|v|-N|r|v|r|;d33=-Nr-N|v|r|v|-N|r|r|r|.
假设1干扰di(t)(i=1,2,3)是未知时变函数,且有界,存在一个未知正上界dmax满足
‖di(t)‖∞≤dmax.
(2)

引理2对于一个非线性系统


(3)
式中:p2、p3和r为参数,p2=k(t*),p3>0,r>0.其中t*为k(t)取得最大值的时刻,k(t)存在一个上界K*,满足
k(t)≤K*, ∀t>0.
(4)
1.2 屏障函数

(5)
2 主要结果
船舶的期望轨迹是ηd,对于控制器是已知的,跟踪误差定义为
(6)

(7)
滑动变量设计如下:
(8)
式中:c1为滑模参数,c1>0.式(8)求导得
(9)
使用等效滑模控制方法,控制输入选择以下形式:
τ=τeq+τs,
(10)
式中:τeq为滑模控制中的等效项,计算式为
τeq=(C(υ)+D(υ))υ-
τs为滑模控制中的鲁棒项,τs=-MR-1(ψ)K(t,si(t))sgn(s(t)),其中滑模自适应增益K(t,si(t))=diag[K1,K2,K3].
定理1考虑ASV系统动态公式(1)和未知干扰d(t)满足假设1和控制输入公式(10),如果鲁棒项中的K(t,si(t))选择下式:
(11)
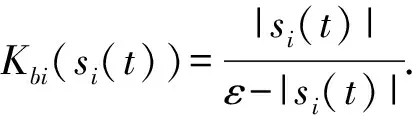
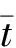

(12)
由引理2可知,存在一个正常数K*,满足K*>K(t),∀t>0,选取如下李雅普诺夫函数:

(13)


(14)


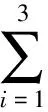

(15)

(16)

(17)

(18)

(19)


,
(20)
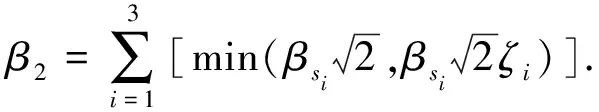
3 数值仿真
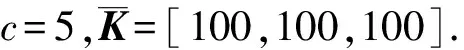
采用本研究方法设计控制器,并进行仿真,船舶的航行轨迹和轨迹跟踪误差如图1和2所示.由图1-2可知,实际轨迹在很短的时间内就能够收敛于理想轨迹.
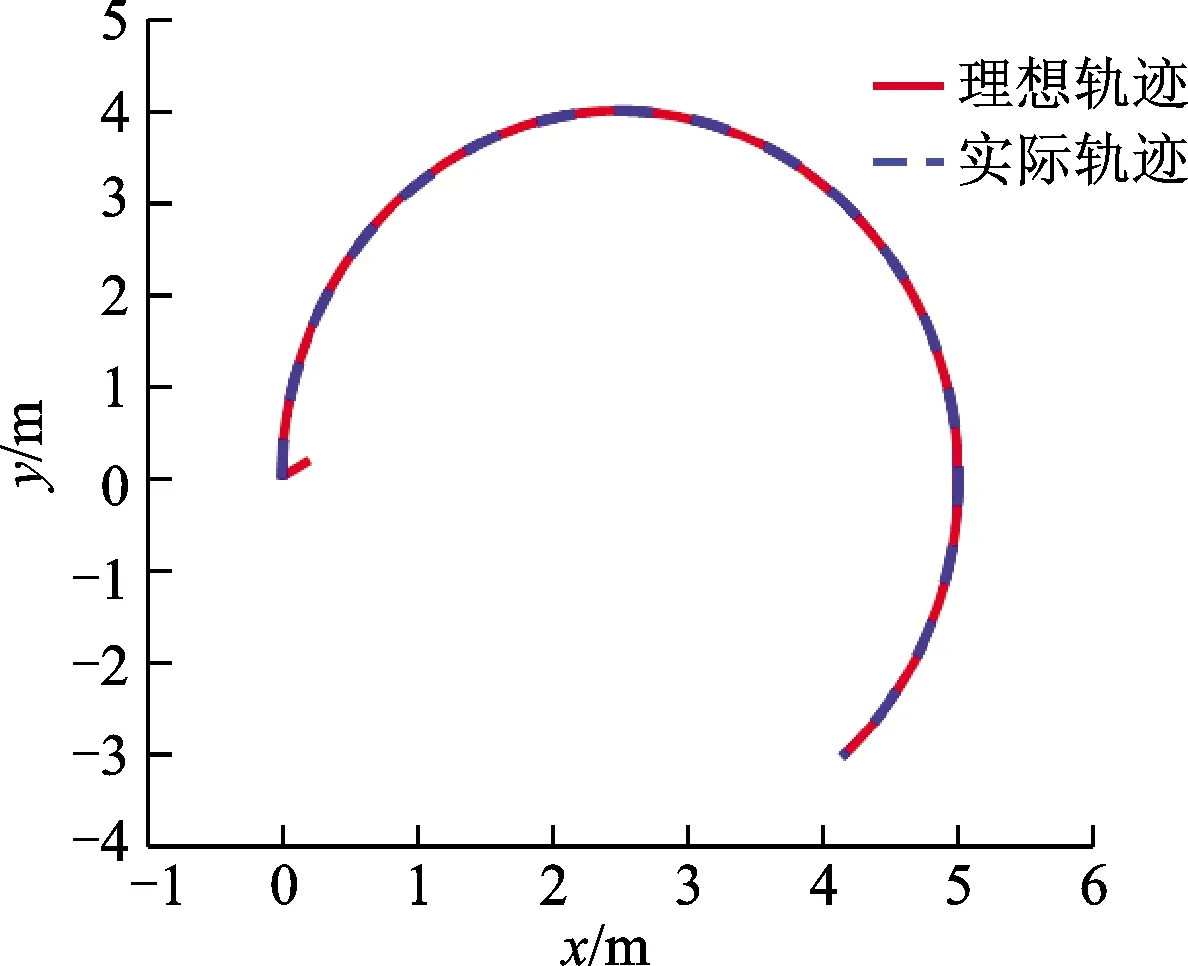
图1 ASV实际运行轨迹和理想轨迹

图2 轨迹跟踪误差
图3、4分别为滑动变量、滑模控制增益与时间的关系曲线.

图3 滑动变量与时间关系曲线


图4 滑模控制增益与时间关系曲线
系统的控制输入与时间关系曲线如图5所示,初始阶段的控制增益单调增加会使初始阶段的系统输入变大,当系统切换至屏障函数自适应阶段,输入的幅值减小,且系统输入的抖振大大减小.

图5 控制输入与时间关系曲线
4 结 论
1) 笔者针对船舶轨迹跟踪问题,提出一种基于屏障函数的自适应滑模控制方法,利用屏障函数来自适应调节滑模增益,保证增益不会被过高估计.
2) 控制器设计过程中不需要任何关于外部干扰的先验信息,并且保证滑动变量收敛保持在一个预定义的零的领域内,从而保证船舶轨迹跟踪的性能.
3) 通过Lyapunov理论分析证明系统的稳定性,仿真结果表明控制器设计的控制器具有良好的动态特性.
