往复剪切作用下砂泥岩混合料力学特性分析

吴 晓

(安徽省城建设计研究总院股份有限公司，安徽 合肥 230051)

三峡库区广泛分布三叠系互层状的砂岩和泥岩地层，河岸港口、道路及房屋等基础设施建设时常用陆侧挖方料填筑滨水侧，挖填平衡后增加陆侧使用面积，如重庆寸滩港、云南水富港等。作为优质填料的砂岩颗粒料中难免混有泥岩颗粒，称之为砂泥岩混合料[1]。母岩强度刚度的差异性使得砂泥岩混合料力学特性有别于单一岩性颗粒料[2]，单向剪切手段难以反映混合料在货物堆载、波浪、地震等周期性荷载作用下力学行为，为保障工程建设与运行安全，有必要探究往复剪切条件下砂泥岩混合料力学特性发展演化规律。

往复剪切力学性质是土体在周期性荷载作用下力学响应的重要研究课题。大位移与往复剪条件下土体力学特性呈复杂变化规律，模量、刚度与阻尼比是重要的分析指标，Zhou等[3]认为大变形条件下颗粒破碎后填充效应使得土体刚度退化程度降低；Fakharian等[4]指出往复剪切时橡胶颗粒降低了胶砂颗粒混合料的剪切模量与阻尼比；Wang等[5]发现红黏土界面剪切刚度与阻尼比随循环次数增加而减小，抗剪强度与循环荷载无关；齐剑峰等[6]指出大应变条件轴向偏差应力对剪切模量与阻尼比存在显著影响。应力应变变化规律是理论分析的重要依据；Zhang等[7]认为大位移单向剪切时剪应力随剪切位移增大而减小，并趋于稳定；孔亮等[8]发现在慢速往复荷载下砂土应力应变曲线呈卸载非线性，伴随塑性变形产生，存在显著滞回效应；杨光等[9-10]认为粗粒料往返加载中往复应变与残余应变随剪应力比增加而增大。另外，Saberi等[11]指出土体循环剪切作用下应力弱化、软化硬化及颗粒破碎均源自颗粒界面力学作用，并建立了三维本构模型；陈晓平等[12-13]通过含粗粒细粒滑带土往复剪切试验认为黏聚力在大位移剪切后消失，摩擦特性在往复8次后达到稳定，体现为剪切强度循环弱化的变化量较小。

往复剪切条件下砂泥岩混合料因含有软岩颗粒而存在变异性，其力学特性较为复杂。通过增加自动测力与数据同步采集系统将单向剪切改进为往复剪切直剪仪，并进行砂泥岩混合料往复剪切条件下力学特性试验；根据剪应力-位移曲线与剪切强度分布，分析滞回圈面积、阻尼比与剪切刚度随往复次数的变化趋势，揭示砂泥岩混合料力学特性演化规律，拓展其工程应用范围。

1 循环剪切试验

ZJ型应变控制式直剪仪采用量力环测定土样单向剪切过程水平力，难以测定往复剪切条件下应力变化。通过增加自动测力计装置与数据采集系统将其改进成可进行往复剪切试验的直剪仪，主要构件见图1；改进后水平剪应力τ和水平位移s均采用东华DH5902测试系统进行数据同步采集，采样频率为20 Hz，水平剪切力量程为±1.5 kN，其余试验操作方法与原仪器相同。

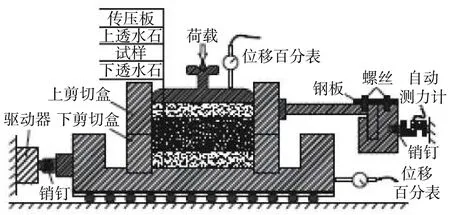
图1 改进后往复剪切直剪仪Fig.1 Improved reciprocating shear direct shear instrument

试验所用土料母岩取自重庆某港口陆侧开挖料，为三叠系上统须家河组微风化的砂岩与泥岩；通过室内试验，测定其力学参数[14]见表1。母岩经过机械破碎、初次筛分、恒温110℃烘干与二次振动筛分得到不同粒组的砂岩和泥岩颗粒。砂泥岩混合料采用同级配按质量比8∶2进行配制土样，其级配曲线见图2。从图2可知，土体不均匀系数Cu为 6.711、曲率系数Cc为1.398，为级配连续且均匀的砂。采用直径61.8 mm、高20 mm的环刀在模具内切样来制备试样，设定土体初始干密度为1.8 g/cm3，含水率为8.0%。

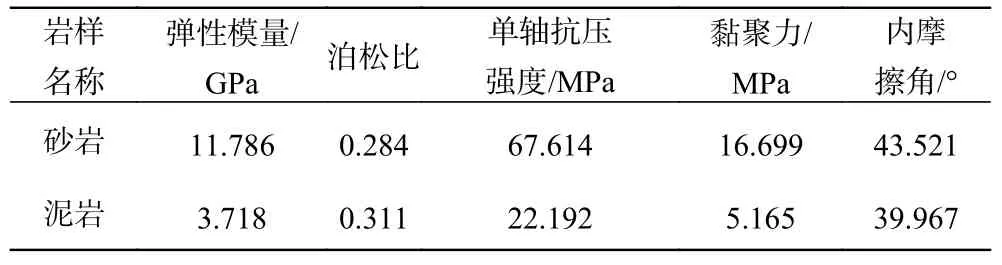
表1 砂岩与泥岩力学参数Tab.1 Mechanical parameters of sandstone and mudstone

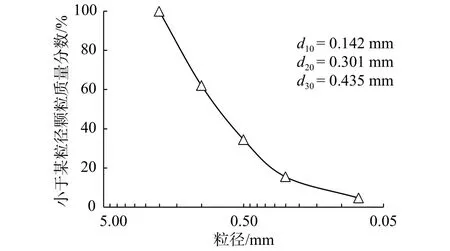
图2 粒径级配曲线Fig.2 Particle size grading curve

结合砂泥岩混合料现场填筑高度与应力状态，采用固结慢剪进行往复剪切试验；设定法向荷载σ1为 100、200、300及 400 kPa四种应力水平，往复剪切次数N为8次，剪切速率为0.8 mm/min，单向剪切位移2s为14.0 mm。特别地，当N=0时即为常规直剪试验。因试验过程中难免存在破坏面部分颗粒脱落、外溢等现象，为保证试验结果可靠性，每组试验后立即测定试样质量，并计算质量损失，若超过1.0%，则重新进行该组试验。

2 试验结果

2.1 往复剪切力学指标

土体在往复剪切作用下水平剪切应力τ随剪切位移s的曲线存在滞回现象[15]，其示意图见图3。为方便后续分析，将A点记为起点，D点为终点，称为正向，正向剪切强度为τm；称为反向，反向剪切强度为−τn（负号表示方向）。根据土动力学理论，采用式（1）与式（2）分别计算土体剪切刚度K与阻尼比d；根据功能关系，滞回圈ACDFA的面积SACDFA（记为S）表征在一次往复剪切过程中克服颗粒阻力所需能量，其大小能反映剪切面上颗粒磨圆程度。特别地，当N=0时，路径为常规直剪试验曲线，其峰值割线模量为土体初始剪切刚度K0。

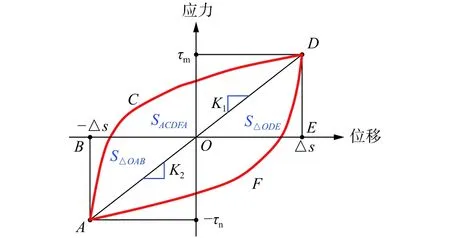
图3 滞回曲线中力学指标示意Fig.3 Mechanical index in the hysteresis curve

式中：τm、τn、s、SACDFA、S△OAB及S△ODE见图3 所示。

2.2 剪应力-位移曲线

采用图3所示方法整理往复剪切试验数据，得到不同σ1与N下τ-2s曲线（见图4）。从图4可知，随着N增大，S逐渐减小，其中第1次减小幅度显著大于其余各次；单向的τ-2s曲线从应变软化逐渐转为应变硬化，残余强度趋于稳定；剪应力τ随σ1增加而增大，正反改变方向处存在剪应力跳跃现象，跳跃幅度随σ1增加而降低。

图4 不同σ1时τ-2s曲线Fig.4 τ-2s curves at different values of σ1

2.3 正反向剪切强度

依据图3整理图4各次正向与反向剪切强度，并绘制其随N的分布（见图5）。从图5可知，当σ1相同时，τm与τn均随N增大而逐渐减小，并趋于稳定；N相同时，τm稍大于τn，两者近似关于“0”对称分布。

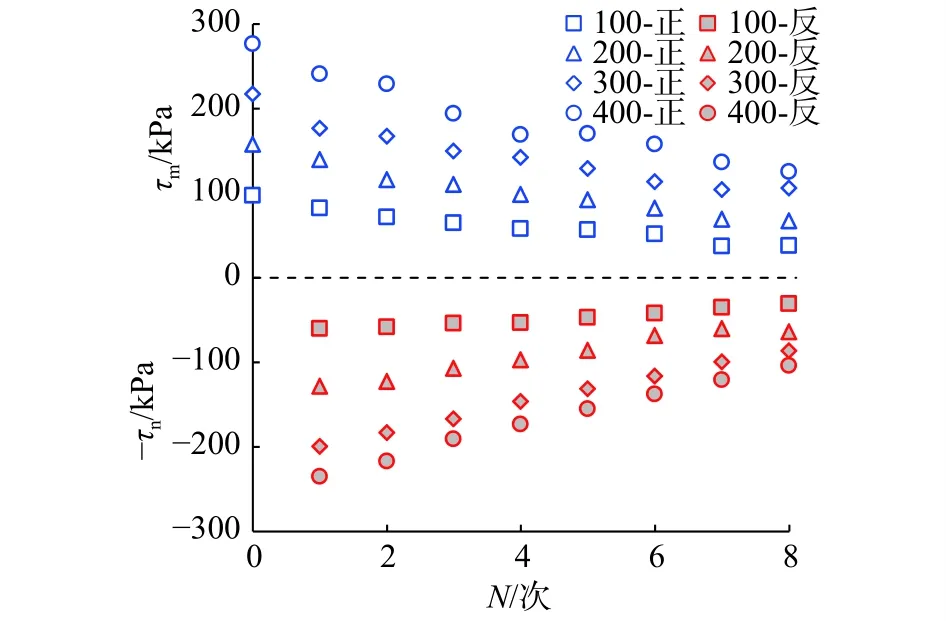
图5 正反剪切强度τ-N分布Fig.5 Positive and negative shear strength τ-N distribution

3 力学特性演化分析

3.1 N=0时力学特性

提取图4中常规直剪试验结果，绘制τ随剪切应变γ（剪切位移s与试样直径61.8 mm的比值）曲线（见图6）。在图6中，τ-γ曲线为应变软化；随σ1增加，峰值强度增大，且其斜率(K0,σ1)也逐渐增大，这说明砂泥岩混合料剪切刚度与法向应力密切相关，法向应力越大，土体越密实，剪切刚度越大。在同一坐标系绘制K0,σ1随σ1/σa分布（σa为1个标准大气压力，取101 kPa），从图7可知，K0,σ1-σ1/σa线性关系显著，采用线性函数拟合，得到其数学表达式见式（3）。

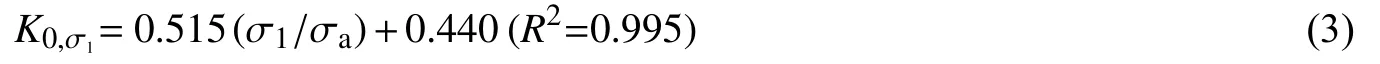
图6 N=0时τ-γ曲线Fig.6 τ-γ curve when N=0

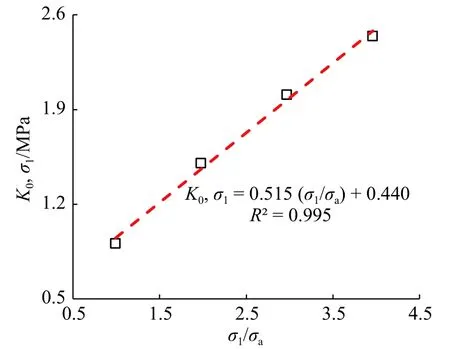
图7 K 0,σ1-(σ1/σa)分布Fig.7 K 0,σ1-(σ1/σa) distribution

3.2 往复剪切作用

3.2.1 滞回圈面积S与阻尼比d根据图3和式（2）整理图4中试验数据，得到σ1下S随N变化分布见图8；d随N变化分布见图9。从图8可知，S随N增加而逐渐减小，并趋于稳定；σ1越大，这种变化趋势越显著。在图9中，不同σ1时，d随N增加呈缓慢增大的趋势，但其增大区间仍处于较小范围；不同σ1时d-N分布相似，即d的变化与σ1无关。

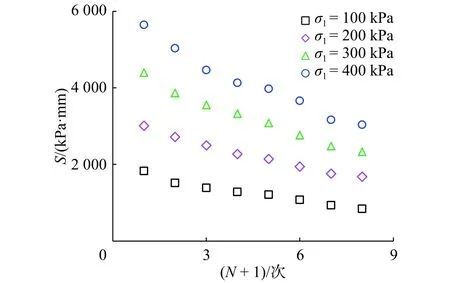
图8 S随N变化分布Fig.8 S varies with N

图9 d随N变化分布Fig.9 d varies with N

3.2.2 剪切刚度K剪切刚度K是表征土体抵抗应力剪切作用能力的重要度量。因软岩颗粒的存在，需查明砂泥岩混合料K值的计算方法。文献[5]采用自然对数函数拟合不同粗糙度下剪切刚度随往复剪切次数关系，根据前述K0,σ1研究结果，σ1对砂泥岩混合料K值存在影响。因此，用比值法消除量纲，采用曲线拟合形式建立考虑σ1及N作用的计算K值方法。

整理图3数据，得到不同σ1及N时土体K；在同一坐标系下绘制K/K0,σ1随N变化分布见图10所示。由图10可知，K/K0,σ1随N增加呈减小变化趋势，采用对数函数拟合其分布见式（4），相关程度R2为0.986，拟合效果显著。

图10 K /K0,σ1随N变化分布Fig.10K/K0,σ1 varies with N

确定σ1与N的边界条件，将式（3）代入式（4），即得到考虑σ1及N作用的砂泥岩混合料K值经验计算方法，见式（5）。

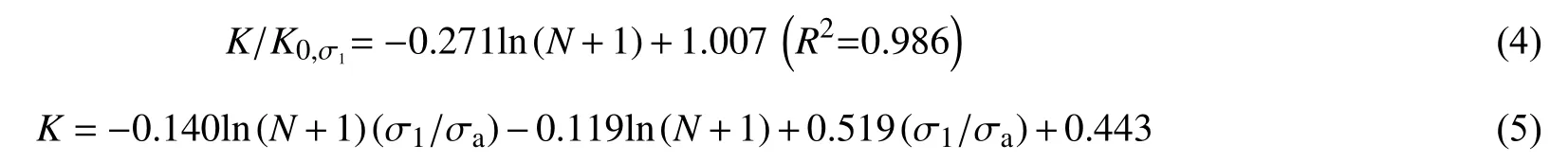
式中：0≤N≤8；0＜σ1≤400 kPa；σa=101 kPa。

式（5）是砂泥岩混合料在三向应力状态下根据不同次数往复剪切试验结果所建立的经验式，σ1的边界条件为 0<σ1≤400 kPa，N为 0≤N≤8。当N=0 时，式（5）等价于式（3），但其系数是式（3）的 1.007 倍，这相当于放大了原有K值，不利于评价土体抵抗剪切变形特性。若为了工程使用简便性，可将式（4）的常数项调整至1.000或小于1.000的数值，以增加安全储备。因此，在使用式（5）时应特别注意边界条件。

将往复剪切试验的σ1及N代入式（5），得到K在不同σ1及N工况下的试验值与计算值（见图11）。从图11可知，计算值与试验数据的吻合程度较高，这表明所建立的计算方法能描述砂泥岩混合料在不同法向应力与往复剪切次数下的剪切刚度变化规律。

图11 K的试验值与计算值Fig.11 Test and calculated values of K

4 讨论与分析

4.1 剪切过程颗粒行为响应

散粒体材料粒间接触类型按接触几何形态分为点-点、点-面与面-面三种[16]，砂泥岩混合料还存在不同岩性颗粒间接触类型，即砂-砂、泥-泥和砂-泥颗粒接触；前两类接触类型在力学机制响应上存在相似性，可合并为一种。因此，砂泥岩混合料粒间接触按岩性分为同质颗粒接触与异质颗粒接触两种（见图12）；其中，(a)→(b)→(c)为同质颗粒接触力学响应，(d)→(e)→(f)为异质颗粒接触力学响应。

图12 颗粒接触力学响应示意Fig.12 Schematic diagram of particle contact mechanics response

在图12中，同一外荷载作用下，颗粒间接触部位存在应力集中现象，即(a)与(d)阶段；随着位移等边界条件的变化，同质颗粒的粒间作用体现为以镶嵌等空间位置调整、粗面磨蚀或棱角挤碎等力学响应，即(b)阶段；因泥岩颗粒强度低于砂岩颗粒，此时异质颗粒的粒间作用主要体现为泥岩颗粒的破碎效应，即(e)阶段。若外部条件再次变化，同质与异质颗粒棱角进一步磨灭，周围产生更多细小颗粒，土体浑圆度减小，即(c)和(f)阶段。

除了颗粒间力学响应机制以外，镶嵌、咬合、平移、旋转、翻越等颗粒间空间相对位置调整也是影响土体宏观强度与变形的重要因素。随着往复剪切持续进行等边界条件改变，砂泥岩混合料颗粒重复上述颗粒间空间相对位置调整与力学响应行为。

4.2 砂泥岩颗粒料强度特性

法向应力是影响砂泥岩混合料应变软化过渡至应变硬化的重要因素。应力愈大，土体颗粒在外荷载作用下相对位置调整频度降低，土骨架相对恒定，宏观体现为应变硬化（见图4）。在往复剪切过程单向剪切作用即将结束阶段，依据颗粒行为响应，剪切面上颗粒排布在原方向上调整至最佳受荷状态；在转变剪切方向时，颗粒间相对位置也突然转向，咬合、镶嵌等位置调整频度在短时间内剧增，宏观体现为图4中剪应力在转变方向时的跳跃现象[5]。

往复剪切过程砂泥岩混合料颗粒物理与力学行为的响应，使得剪切面上抵抗外荷载能力逐渐弱化，正向与反向剪切强度随往复次数增加而降低（见图5）；滞回圈面积、剪切刚度的发展演化机制与强度存在相似性（见图10与图11）。阻尼比是表征材料在外部振动荷载作用下动力衰减机制的重要参数。改进后仪器能进行往复剪切试验，但受加载条件限制，并不能进行高频荷载试验。因此，试验所得阻尼比在较小循环往复次数内存在缓慢增大的现象，这可能是源自剪应力作用下的颗粒破碎效应，与文献[4，17]的结果类似。

5 结 语

（1） 利用改进的往复剪切直剪仪探究了砂泥岩混合料往复剪切力学特性。滞回圈面积随往复剪切次数增大而减小，并趋于稳定，第1次减小幅度显著大于其余各次。剪应力-位移单向曲线随法向应力增大由应变软化逐渐转为应变硬化，转换剪切方向时循环曲线存在剪应力跳跃现象，跳跃幅度随法向应力增加而降低。

（2） 砂泥岩混合料剪切刚度与法向应力和往复剪切次数密切相关。砂泥岩混合料正反剪切强度均随往复剪次数增大而逐渐减小，并趋于稳定，正向强度稍大于反向。阻尼比随往复剪切次数增加而缓慢增大，且与法向应力无关。初始剪切刚度随法向应力呈线性分布，归一化剪切刚度与往复剪切次数呈对数关系，据此建立了考虑法向应力与往复剪切次数的砂泥岩混合料剪切刚度经验计算方法。