含初始条件的基于黏滞阻尼的单自由度振动响应综合研究

王允地，王帅，王良文，张继豪，王若澜

1.陕西科技大学 机电工程学院, 陕西 西安 710021；2.北京立德未来助学公益基金会，北京 100026；3.郑州轻工业大学 机电工程学院, 河南 郑州 450002；4.郑州轻工业大学 国际教育学院, 河南 郑州 450002

0 引言

工程实际中的很多问题都可抽象为单自由度系统的振动[1-3]. 通常，机械系统的黏滞阻尼是非线性的,与温度、频率、应变等因素有关[4-5]. 摩擦也是机械系统中常见的非线性问题之一[6-9]，在考虑系统的黏滞阻尼、摩擦等因素的前提下研究系统的振动非常必要. 针对简谐激励振动，文献[10-11]绘制了相频曲线图和幅频曲线图，但均未给出包含初始条件的简谐激励响应关系式. 文献[12]给出了包含初始条件的小阻尼简谐激励响应式，但未讨论阻尼比为0且激励频率与固有频率相等的情况. 文献[12-13]给出了计算任意激励响应的杜哈米积分，但未讨论库仑摩擦力对振动响应的影响. 文献[14] 研究了单自由度含干摩擦振动系统的全局动力学行为. 文献[15]采用拉普拉斯变换和海维赛德第一类展开式，推导了有阻尼单自由度系统的强迫振动通解. 文献[16]考虑了具有非线性黏滞阻尼和库仑摩擦的单自由度系统，描述了从系统的自由响应信号中同时识别非线性阻尼和库仑摩擦的方法. 文献[17]讨论了纯库仑摩擦力对自由振动影响. 文献[18]用相图法就库仑摩擦力对强迫振动的影响作了一些定性讨论.文献[19]提出了一种估算库仑和黏滞摩擦的减量方法.文献[20]提出了将单自由度系统自由振动响应的封闭解作为动力系统库仑摩擦基础研究的一部分.

上述研究对含初始条件的基于黏滞阻尼的单自由度振动计算问题研究不够全面. 本文拟在现有研究成果的基础上，对包含初始条件的基于黏滞阻尼的自由振动响应和简谐激励响应进行研究，分析有阻尼共振和无阻尼共振，以及无阻尼振动响应中存在的拍振现象，探讨库仑摩擦力对系统振动的影响等，以期丰富单自由度系统振动理论的研究，为在工程中更好地应用单自由度振动系统提供支持.

1 黏滞阻尼自由振动响应

对物体质量为m、刚度为k、黏滞阻尼系数为c、激励力为F(t)(作用方向为物体的运动方向X)的质量、弹簧、阻尼系统，有振动方程[21]：

①

对于支座沿X方向以s=s(t)作激励运动的情形，将上式中F(t)换为ks(t)即可，并称其为等效激励力. 激励力为0的振动即为自由振动，可将式①转化为

②

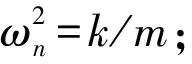
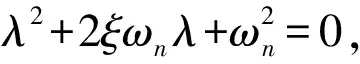
若ξ>1，λ1和λ2均为负数，位移x随着时间t的增加从初始位置起迅速趋于0，或沿速度方向运动到极值点再迅速趋于0.

多数情况下，ξ<1. 在复数范围内，虚指数函数的线性组合等于三角函数的线性组合，解表达式的实部和虚部均成为负指数函数与三角函数的乘积. 取其实部推得包含初始条件的小阻尼自由振动响应x为

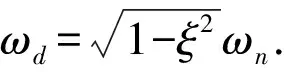
如果出现ξ=0的理想情况，系统就会按ωn为角频率的简谐规律一直振动，故ωn称为固有频率.

2 黏滞阻尼简谐激励响应

2.1 稳态响应及幅频和相频曲线

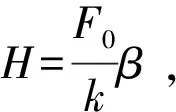
固定ξ，让ω/ωn从0向无穷大变化，则有：ω/ωn=0时，β=1，H=F0/k，α=0；ω/ωn=1时，β=1/(2ξ) ，α=π/2；ω/ωn→∞时，β趋于0，α趋于π.

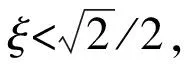
若ξ>0，随着时间增长，齐次微分方程的通解幅值以负指数规律趋于0，只剩下与激励力频率ω相同的稳定简谐特解部分. 通常称其为由激励力引起的稳态响应：

值得注意的是，在ω/ωn=1附近，ξ对β影响较大，对其他参数影响较小. 另外，若ξ较小，则当ω/ωn=1时，β接近于最大值，而α仍不受ξ的影响，恒等于π/2. 这也是当ω/ωn=1时发生共振的原因.

图1是给定ξ后，β及α随ω/ωn变化的幅频曲线图和相频曲线图. 从图1可以看出，在ω/ωn=1附近，随ξ减少，β显著增加，且在ω/ωn=1时，α不受ξ的影响.

图1 给定ξ后，β及α随ω/ωn变化的 幅频曲线和相频曲线图Fig.1 Amplitude frequency curve and phase frequency curve for β and α changing follow ω/ωn when ξ was given

2.2 包含初始条件的响应计算

强迫振动微分方程的通解等于强迫振动方程特解与对应的齐次微分方程通解之和. 再考虑初始条件，即得方程的完整响应式. 阻尼比ξ≥1的情况较少见，在此不加讨论.

情形1阻尼比1>ξ>0

当阻尼比1>ξ>0时，响应x由瞬态衰减项和稳态响应项组成.

令激励力F=F0cosωt，则有：

令激励力F=F0sinωt，则有：

令激励力F=F0cos(ωt-φ)=F1cosωt+F2sinωt，其中F1=F0cosφ，F2=F0sinφ，则有：

该完整响应式第一项为自由振动项,第二项为伴随自由振动项,第三项为稳态响应项. 自由振动项由初始条件x0和v0决定，随着时间趋于0. 伴随自由振动项与初始条件无关，也随着时间趋于0. 将该式中的时间t换成t-t0,即可得到t=t0时,位移为x0且速度为v0的响应计算式.

情形2阻尼比ξ=0

当阻尼比ξ=0时，响应x由固有振动项和激励响应项组成.

若ω<ωd，分别令激励力F1=F0cosωt，F2=F0sinωt，F=F1cosωt+F2sinωt，则可以推导出：

其中β=1/[1-(ω/ωn)2].

若ω>ωd，则类似可以推导出：

其中β=1/[(ω/ωn)2-1].

若ω=ωn,可以推导出：

2.3 共振曲线的过渡过程及拍振现象

由于简谐激励响应规律与激励相角无关，因此只讨论纯余弦激励的情况.

2.3.1 有阻尼共振曲线当初始位移x0=0、速度v0=0时，令激励力F=F0cosωnt，则共振响应x为

其中，β=1/(2ξ)，α=π/2.

在阻尼比ξ较小的情况下，ωd≈ωn，x的响应式可简化为

图2给出了有阻尼共振响应计算实例结果，其中m=0.1 kg，c=0.2 N·s/m，k=10 N/m，F0=10 N，ω=ωn=10 rad/s，β=5，x0=0 m，v0=0 m/s，a0=100 m/s2. 从图2可以看出，振幅以负指数规律先以较快速度上升，然后缓慢上升到稳态值.

图2 有阻尼共振响应曲线Fig.2 Damped resonance response curve

2.3.2 无阻尼共振曲线当阻尼比ξ=0时，取初始位移、速度及激励力与有阻尼的状态相同，其共振响应x为

图3给出了一个相应的计算实例结果，其中m=0.1 kg，c=0 N·s/m，k=10 N/m，F0=10 N，ω=ωn=10 rad/s，x0=0 m，v0=0 m/s，a0=100 m/s2. 从图3可以看出，该理想响应振幅以线性规律从0起一直上升.

图3 无阻尼共振响应曲线Fig.3 Undamped resonance response curve

2.3.3 无阻尼振动的拍振现象取初始位移及速度均为0，令激励力F=F0cosωt，激励频率ω接近于ωn，当ω<ωn时,振动响应x为

其中β=1/[1-(ω/ωn)2].

当ω>ωn时，振动响应x为

其中β=1/[(ω/ωn)2-1].

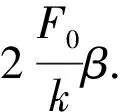
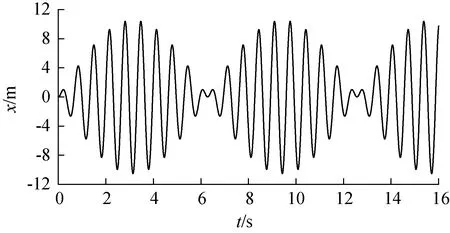
图4 拍振曲线Fig.4 Beat vibration curve

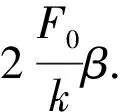
3 库仑摩擦力对系统振动的影响

质量块在轨道上运行时，通常存在库仑摩擦力K，把振动微分方程①中的F(t)换为激励力F1(t)和速度反向库仑摩擦力K的迭加，即可用杜哈米积分解析分析或用龙格-库塔法数值计算出库仑摩擦力对自由振动和强迫振动的影响.

3.1 库仑摩擦力对自由振动的影响

3.1.1 纯库仑摩擦力对自由振动的影响通过大量的实例计算，并结合文献[11]可知，纯库仑摩擦力作用下的自由振动幅值以等差级数下降，幅值从极小到极大或从极大到极小均为以ωn为角频率的余弦函数与常量之和，异侧相邻幅值下降量为摩擦力与刚度系数比值的2倍，同侧相邻幅值下降量为其4倍. 幅值下降到3倍以下后会进入平衡位置附近而停止不动.

图5给出一个用龙格-库塔法计算的纯库仑摩擦力对自由振动的影响实例，其中K=1.5 N，m=0.1 kg，k=10 N/m，c=0 N·s/m，F0=0 N，ωn=10 rad/s，x0=4 m，v0=4 m/s，FK=1.5 N. 从图5可以看出，振动幅值以等差级数下降的规律明显.

图5 纯库仑摩擦力对自由振动的影响Fig.5 Effect of pure Coulomb friction on free vibration

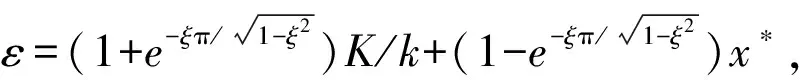
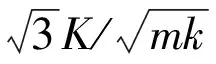
3.2 库仑摩擦力对强迫振动的影响

机械振动曲线大多表现为方向不断变化的振荡曲线. 从负位移幅值处向正位移幅值处运动时，库仑摩擦力为负常量；而从正位移幅值处向负位移幅值处运动时，库仑摩擦力为正常量. 使得系统位移与无库仑摩擦力位移有缩减差别量ε. 据此，利用和函数积分的迭加性，用杜哈米积分分段推出了由刚度系数k、固有频率ωn、阻尼比ξ、负位移幅值时间t0和正位移幅值时间t1所决定的库仑摩擦力K对位移差别的影响式为

把获得的库仑摩擦力K对位移差别的影响式和其他激励力F1(t)引起的响应式合并，即可得到系统的最终响应式.

选取合适的时间步长h，用数值算法得到库仑摩擦力K=1.5 N对激励力F1(t)=F0sinωt的强迫振动影响曲线如图6所示.

图6 库仑摩擦力对强迫振动的影响Fig.6 Effect of Coulomb friction on forced vibration

由图6并结合库仑摩擦力K对位移差别的影响式可知，振动响应加速度的绝对值在位移幅值处产生由大到小的不连续变化，其差值为库仑摩擦力K与质量m比值的2倍. 经进一步推导显示，区间内消耗的能量等于位移行程与库仑摩擦力的乘积.

当初始位移、初始速度、激励力幅值三者各小于一定值时，质量块运动到位移幅值处时，动摩擦力消失，而静摩擦力则由一个较小值自适应渐变到K，然后质量块开始返回，出现位移幅值处暂停现象. 开始停歇时，加速度突变；停歇结束时，加速度连续.

通过数值计算，结合文献[12]的研究还发现，小库仑摩擦力抑制不住无黏滞阻尼共振响应不断增长的趋势，接近于激励力幅值F0的大库仑摩擦力K才能使无黏滞阻尼共振响应幅值不超过稳态值，并可能出现位移幅值处暂停现象.

4 结语

本文通过对基于黏滞阻尼的单自由度振动响应及简谐激励响应的分析，得到了不同阻尼比状态下的振动位移的变化规律：在简谐激励的情况下，当初始位移及速度均为0，无阻尼激励频率接近于固有频率时，振动系统将出现拍振现象；而小库仑摩擦力抑制不住无黏滞阻尼共振响应的不断增长趋势；接近于激励力幅值的大库仑摩擦力才能使无黏滞阻尼共振响应幅值不超过稳态值，并可能出现位移幅值处暂停现象. 这些结论为进行机械振动系统的阻尼与摩擦设计奠定了理论基础.