求解0-1背包问题的改进树种优化算法

张 小 萍

(广西大学计算机与电子信息学院， 广西 南宁 530004)

0-1背包问题是一个经典的NP-hard问题，也是一个组合优化问题。0-1背包问题在生产和生活中应用较广，如物件装箱、投资组合和金融决策等，因此，0-1背包问题受到很多学者的关注。0-1背包问题可描述为：有D件物品，每件物品不可分割，第j件物品(j=1，2，…，D)的重量是wj，价值是pj，现有一个承载重量限制为C的背包，如何选择物品放入背包使得背包中物品的总重量不超过C且物品的总价值达到最大。0-1背包的数学模型可以表示为：

xj∈{0，1}，j=1，2，…，D

(1)

求解0-1背包问题的算法包括动态规划法、递归算法和回溯法等确定性算法，这类算法能够求解出问题的全局最优解，但是算法的时间复杂度与问题的规模呈指数关系，只能用于求解维度比较小的0-1背包问题。而智能优化算法只能求解出0-1背包问题的最优解域，不一定能够求解出全局最优解，但智能优化算法的时间复杂度比较低，可以用于求解高维的0-1背包问题。随着智能优化算法的发展，涌现出多种用于求解0-1背包问题的算法，这些算法在基本算法的基础上加入了改进策略来加快算法的收敛速度。周洋等人[1]在基本粒子群算法中加入贪婪策略(GOPSO)求解0-1背包问题，提高了算法的收敛性能。任静敏等人[2]通过在基本萤火虫算法中加入惯性权重、变异算子和贪婪策略(WGFA)，提高了算法的全局搜索能力。刘雪静等人[3]改进了乌鸦算法(BCSA)，先利用Chebyshev映射产生混沌序列初始化种群，使种群的初始分布比较均匀，然后使用贪婪策略修复不可行解和对可行解进行优化。周洋等人[4]设计了一个离散鸡群算法(DCSO)，引入了自适应权重组合变异算子来更新公鸡个体位置，采用定向变异策略改进了种群中小鸡位置的更新方式，这样的改进使得算法寻优时能够避免盲目的随机搜索，进一步提高了算法的稳定性。这些算法在求解0-1背包问题时获得了较好的优化效果，但随着物品数目的增加，求解问题难度加大了，算法存在着收敛速度慢，难以获得全局最优解的问题，算法需要进一步优化。

1 基本树种优化算法

树种优化算法(TSA)[5]是一种新兴的智能优化算法，是2015年由 Kiran 提出的，算法的思想是模拟大自然树木生长繁衍的过程。树种优化算法的结构简单，寻优能力较强，在彩色图像多阈值分割[6]、短期电力负荷预测[7]和结构损伤识别等领域中应用都获得了较好的效果。

在树种优化算法的初始化阶段，使用式(2)生成一批树木：

Ti，j=Lj+ri，j(Hj-Lj)

(2)

式中：Ti，j是树木i位置的第j个元素；ri，j是[0，1]中的随机数；Hj是搜索空间的最大值；Lj是搜索空间的最小值。若优化问题是最小值问题，需要利用式(3)找到当前最优树的位置：

B=min{f(Ti)}，i=1，2，…，N

(3)

然后，树木要生成种子，TSA使用了2种机制来生成种子在全局搜索和局部搜索中获得平衡，利用式(4)或(5)生成种子：

Si，j=Ti，j+αi，j(Ti，j-Tr，j)

(4)

Si，j=Ti，j+αi，j(Bj-Tr，j)

(5)

式中：Si，j表示第i棵树繁衍的第i个种子的第j个元素；Tr，j表示第r棵树位置的第j个元素；Bj表示当前最优树的位置的第j个元素；αi，j是[-1，1]中的随机数，表示步长因子。

式(4)侧重于全局搜索，避免算法进入局部最优解，式(5)侧重于局部搜索，便于算法能够快速收敛。TSA的算法流程如下：

Step 1 种群初始化。设种群数目为N，问题维度为D，设定一个搜索趋势常数为ST，使用式(2)对N棵树木的位置Ti，j进行初始化，利用式(3)计算出当前最优树的位置B。

Step 2 生成种子。确定每棵树生成种子的数量，在每个种子生成时，产生一个随机数λ，若λ>ST，使用式(4)生成种子，否则使用式(5)生成种子。

Step 3 选择最优解。在每棵树Ti生成的种子中选择出一个最优解，与当前的树Ti作比较，若比树Ti更优，则用种子取代树的位置。

Step 4 迭代次数加1，然后判断是否达到最大迭代次数，如果不满足就跳转到 Step 2，否则输出最优解，算法结束。

2 改进的树种优化算法

2.1 二进制编码

基本的树种优化算法是求解连续问题的，而0-1背包问题是离散问题，要先对可行解进行二进制编码。设D表示问题的维度，将实数型的向量Ti=[Ti，1，Ti，2，…，Ti，D]编码为二进制向量Yi=[Yi，1，Yi，2，…，Yi，D]，编码规则如下：

(6)

2.2 贪婪策略

由于在0-1背包问题中还需要符合不超过背包承重限制的约束条件，因此经过二进制编码之后可能会出现不符合约束条件的不可行解，目前在0-1背包问题求解中，对不可行解有2种处理方法，一是使用惩罚函数，二是使用贪婪策略。总体来说，使用贪婪策略要比使用惩罚函数的性能好，因为使用贪婪策略既可以对不可行解进行修复，变为可行解，又可以对可行解进行局部优化，加快收敛的速度。假设vi表示0-1背包问题中的物品的价值/重量，即vi=pi/wi，贪婪策略的基本过程如下：

Step 1 初始化背包为空，按照vi从大到小的顺序对二进制编码Yi=[Yi，1，Yi，2，…，Yi，D]选择的商品(相应比特位为1)进行检查，如果已选择的商品加入背包后，小于等于背包重量限制，就加入背包；否则，取出该商品，则Yi相应的比特位置为0。

Step 2 按照vi从大到小的顺序对二进制编码Yi=[Yi，1，Yi，2，…，Yi，D]未选择的商品(相应的比特位置为0)进行尝试性地加入背包，若该未选择的商品加入背包后，小于等于背包总承重，则加入背包，Yi相应的比特位置为1；否则，不加入。

在Step 1后，无论Yi=[Yi，1，Yi，2，…，Yi，D]是否是可行解，都将转为可行解。Step 2主要是对可行解进行优化，使用贪婪思想尽可能地将vi值比较大的物品加入背包，保证背包中的物品价值达到局部最大值。贪婪策略具体的伪代码可以参考文献[1]。

2.3 改进策略

尽管TSA使用了2种机制来生成种子，平衡了全局搜索和局部搜索，但是当算法迭代到一定程度后，种群已经收敛。种群中个体的相似度比较高的情况下，无论是使用式(4)还是式(5)来生成种子都难以获得更好的解的情况下，树木位置无法更新，算法会进入僵化，种群会陷入局部最优解。在这种情况下，为了增加种群的多样性，提高算法的全局搜索能力，借鉴人工蜂群优化算法探索一个蜂蜜源经过多次开采没被更新就重新设置开采蜜源的思想[8]，设定一个阈值H，当Ti有连续H代以上没有更好的种子更新Ti，就使用式(2)对Ti进行重新初始化，其目的是增加种群的多样性。

2.4 改进树种优化算法(ITSA)的具体步骤

Step 1 初始化系统各个参数，迭代次数初始化为0，设定求解问题的维度D，种群大小N，迭代最大次数M，以及ST和H。

Step 2 利用式(2)初始化种群中的树木位置，并用式(6)对树木位置进行二进制编码，然后使用贪婪策略对二进制编码进行修补和优化，计算出个体的适应度。为每棵树木初始化一个计数器Cnti=0。

Step 3 生成种子。确定每棵树生成种子的数量，在每个种子生成时，产生一个随机数λ，若λ>ST，使用式(4)生成种子，否则使用式(5)生成种子，对每个种子进行二进制编码并用贪婪策略修复和优化，计算出每个种子的适应度。

Step 4 选择最优解。在每棵树Ti生成的种子中选择出一个最优解，与当前树Ti的适应度作比较，若比树Ti更优，则用种子取代树的位置，并置Cnti=0；否则，令Cnti=Cnti+1。

Step 5 若Cnti>H，使用式(2)对Ti进行重新初始化。

Step 6 迭代次数加1，然后判断是否达到最大迭代次数，如果不满足就跳转到 Step 3，否则输出最优解，算法结束。

3 实验结果分析

用文献[9]中的4个物品数目分别为17、60、100、200的0-1背包测试案例进行实验，实验环境为8 G内存，CPU为Intel(R) Xeon双核2.4 GHz，使用MATLABR2020b编程。为了公平起见，ITSA的种群数量设为30，每棵树可以生成5个种子，设定H=20，ST=0.5。GOPSO、WGFA、BCSA和DCSO算法的种群数目设为150。所有算法的迭代次数都是200次，对每个测试用例都独立运行20次，测试这些算法的最优解、平均解、最差解以及方差和运行时间等性能指标，获得的实验结果见表1。

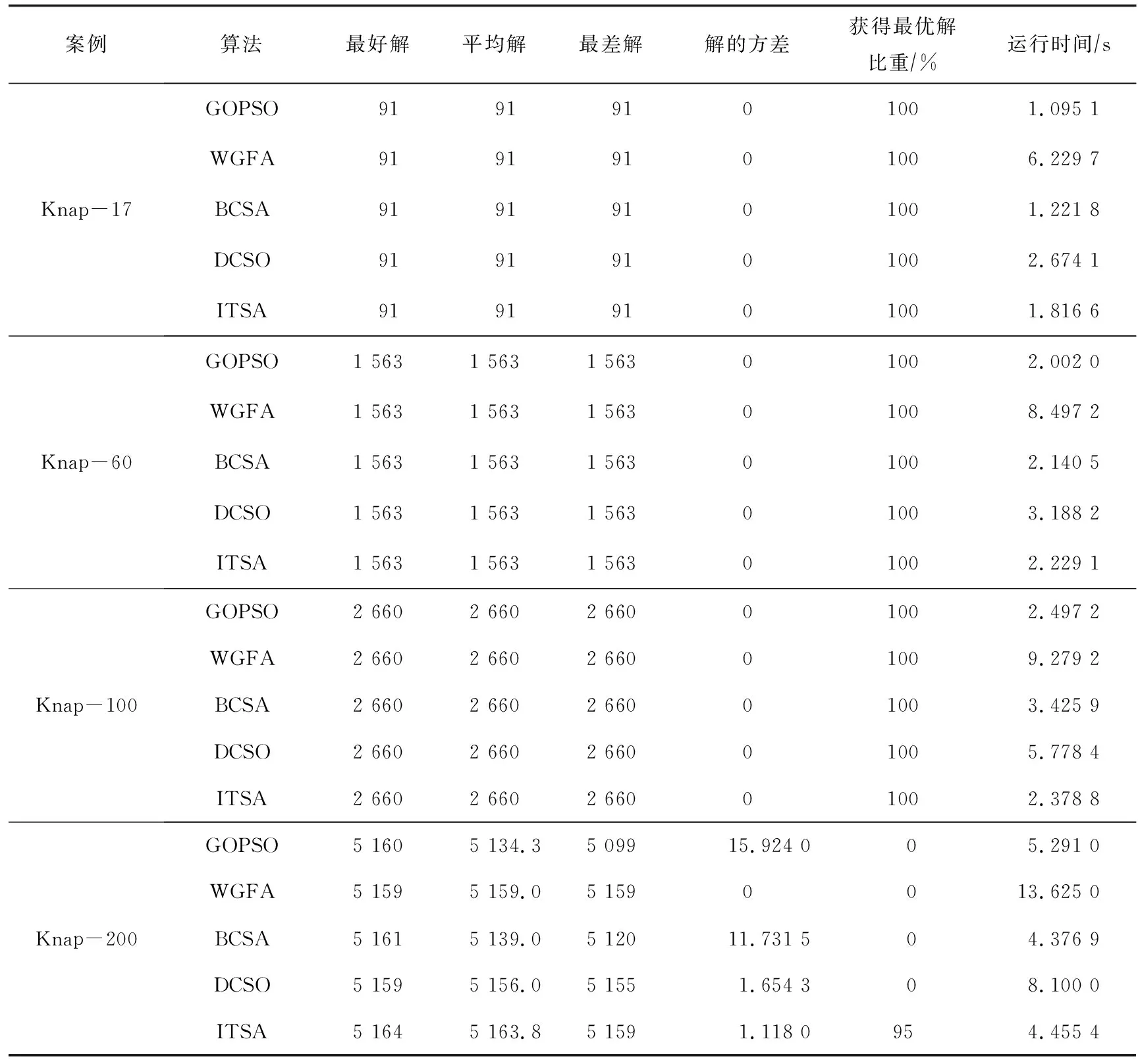
表1 实验结果数据对比

实验数据表明，当物品数量比较小(17，60)时，5种算法都必定可以找到最优解，其中GOPSO的寻优性能比较好，所需要的时间最少，ITSA算法在5种算法所需时间的比较中略高于GOPSO和BCSA，但是当物品数量增大到100时，虽然5种算法都可以找到最优解，但ITSA算法所需要的时间最少，当物品数量增大到200时，只有ITSA算法以95%的概率找到了最优解，其他算法都无法找到最优解，而且ITSA所需时间也比较少，仅仅比BCSA多一点，而BCSA找到的最优解只有5 161，方差也比ITSA大得多。分析发现，ITSA算法在低维和高维的0-1背包问题中都有较好的寻优特性，稳定性比较高，具有较强的鲁棒性。

再使用Knap-100和Knap-200两个案例分析5种算法的收敛性，其收敛曲线如图1、图2所示。

图1 5种算法在求解Knap-100时的收敛曲线

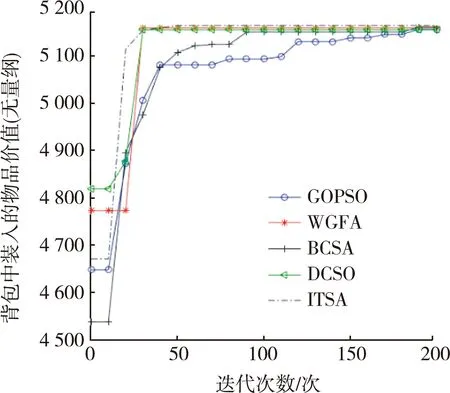
图2 5种算法在求解Knap-200时的收敛曲线

ITSA比其他4种算法的收敛速度更快，收敛到最优解域需要的迭代次数更少，特别是在Knap-200中，只有ITSA收敛到了全局最优解。

4 结 语

树种优化算法是一种新颖的智能优化算法，针对基本树种优化算法容易僵化、在收敛阶段种群个体相似度高、易于得到全局最优解的问题进行了改进，若检测到树木位置连续H代没有更新，就重新初始化数据位置，增加种群的多样性。改进算法结合贪婪策略运用在求解0-1背包问题中，加强了局部搜索的性能。实验结果表明，改进算法在求解0-1背包问题中具有良好的全局搜索性能和较强的稳定性，特别是在高维的0-1背包问题中表现出优越的寻优能力。