区块链电子拍卖中基于身份的盲签名方案

郑 东，范秦铭，郭 瑞，杨 耿

(西安邮电大学 网络空间安全学院,陕西 西安 710121)

互联网信息时代赋予了商品新的交易形式，如电子交易和电子拍卖等。先进的网络技术带给人们便利生活和经济利益的同时，也增加了交易的安全风险和隐患，在人们进行电子交易和电子拍卖的过程中，对个人隐私数据的窃取也与日俱增。电子拍卖[1-2]作为最重要的电子活动之一，是由第三方主持的一种特殊的交易方式，因此，电子拍卖的支付和交易的安全性、公平性和欺诈等问题也日益突显。区块链具有去中心化、数据可靠、交易可追溯等特点，以太坊智能合约提供了一套完整的区块链分布式应用平台，使用以太坊进行数字货币交易时，任何人都可在应用平台上发布和使用分布式系统。引入以太坊智能合约可以为电子拍卖系统提供去中心可信的三方(Trusted Third Party，TTP)服务，以保证拍卖过程的公平性，增强拍卖者对协议的信任程度，扩大协议的适用范围[3-4]。

随着区块链的出现，盲签名[5-7]越来越受到人们的关注。在基于区块链的数字货币、拍卖系统、投票系统以及物联网中，盲签名可以保证合法用户的匿名认证，不可追踪签名者，为需要盲性的系统奠定了基础[8-10]。1983年，Chaum[11]提出了首个用于创建不可追踪支付系统的盲签名，其有用户和签名者两个主要参与者，用户只知道原始消息而不知道签名密钥，而签名者只知道自己签署了消息，并不知道何时签署。盲签名满足了盲性和不可伪造性[12-13]两个主要性质，即：签名者在不知道自己签署了什么的情况下签署了消息，但不能否认自己签署了消息；用户不能伪造签名者的签名。因此，盲签名可以保护用户敏感信息的匿名性，现已广泛应用在投票和拍卖领域。然而，基于盲签名的电子拍卖系统虽然通过电子拍卖协议(Fujioka Okamoto Ohta，FOO)实现了基于盲签名的大规模电子拍卖，但是无抗伪造性和抗共谋性[14]。

基于身份的密码体制[15]是将用户身份加入其公钥中，避免使用公钥证书，简化了密钥的管理过程，减少了证书所造成的开销，同时具有了不可伪造性。基于身份的盲签名[16]可以有效保护签署消息的内容，与用户身份对应的私钥是由可信的第三方密钥生成中心计算并安全地分发给用户，可以有效地抗共谋。因此，拟提出一种应用于区块链电子拍卖的基于身份盲签名方案。在基于身份的盲签名中加人SM3密码杂凑算法，保证其安全性和可靠性，并结合运行在以太坊上的智能合约，构建电子拍卖系统，以期改善电子拍卖过程中存在的安全风险与隐患。

1 基础知识

1.1 盲签名

盲签名[17-18]中椭圆曲线密码体制(Elliptic Curve Cryptography，ECC)是一种基于椭圆曲线离散对数问题难解性的高效密码体制，其使用较短的操作数即可实现与RSA加密算法及离散对数系统相同安全等级的密码服务。与其他公钥算法体制相比，ECC在带宽与复杂度方面性能优势非常明显，并且以太坊在升级后也允许使用椭圆曲线进行加密。

设p是有限域上大于3的素数，椭圆曲线E(Fp)是方程y2=x3+ax+b(modp)在群Fp上的所有解的集合，其中，4a3+27b2≠0 (modp)。

定义椭圆曲线E上的加法，设P=(x1,y1),Q=(x2,y2)，如果x2=x1，y2=-y1，则P+Q=0，否则P+Q=(x3,y3)，其中

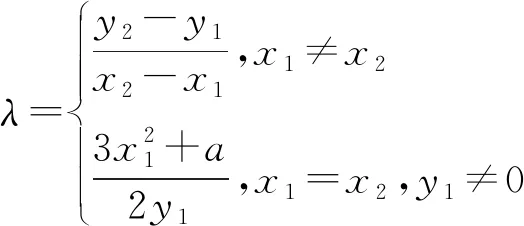
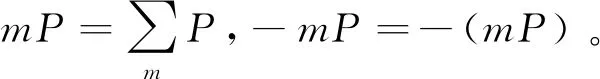
在盲签名过程中，用户先将自己的信息进行盲化，让签名者对于盲化信息进行签名。若m为原始明文消息，u为盲化因子，q为随机数，则盲化处理后的信息为

e=muq(modp)

盲化信息的签名为

s′=ed(modp)

其中，qd=1 (modp)。

对盲化信息的签名进行解盲，得到最终信息的签名为

s=s′u-1(modp)

签名s正确性的验证过程为

uqd=u(modp)
s=s′u-1=edu-1=mduqdu-1=mduu-1=md(modp)

1.2 SM3密码杂凑算法

SM3密码杂凑算法[19]是基础密码算法之一，其将任意长度比特的消息压缩成算法固定的长度，已广泛用于数字签名及验证、消息认证码生成及验证、随机数生成等，并且算法公开，安全性及效率与SHA-256相当。SM3密码杂凑算法的结构是Merkle-Damgard，消息分组长度为512 b，摘要长度为256 b，压缩函数状态为256 b，共64步操作。初始值由8个32 b串联构成，共256 b，压缩函数比SHA-256增加了16步全异或操作、消息双字介入、增加快速雪崩效应的P置换等技术，具有较高的安全性，实现效率也高于或等同于其他密码杂凑算法。

1.3 以太坊

以太坊[20-21]是建立在区块链技术上的去中心应用平台，其网络架构完善且系统性能稳定，是目前主流的区块链平台之一，具有成熟的应用开发语言和技术系统。以太坊智能合约开发语言成熟，能实现多样的以太坊应用，例如，基于以太坊智能合约实现拍卖系统、投票系统等。智能合约只需要达到事先约定好的条件就会触发，而且合约生效后，直到达到条件后才会自动销毁。智能合约在合约层，与算法机制和脚本代码互相配合，以代码的形式将复杂的人工处理环节转化为数字化，自动化的约定协议，大幅降低了处理流程时间，达到瞬时响应瞬时完成的效率。合约的执行过程中，从开始直至销毁，任何形式的故意破坏都不能使其受影响，只会按照事先设定的条件准确执行。智能合约在拍卖系统中的运作机制如图1所示。

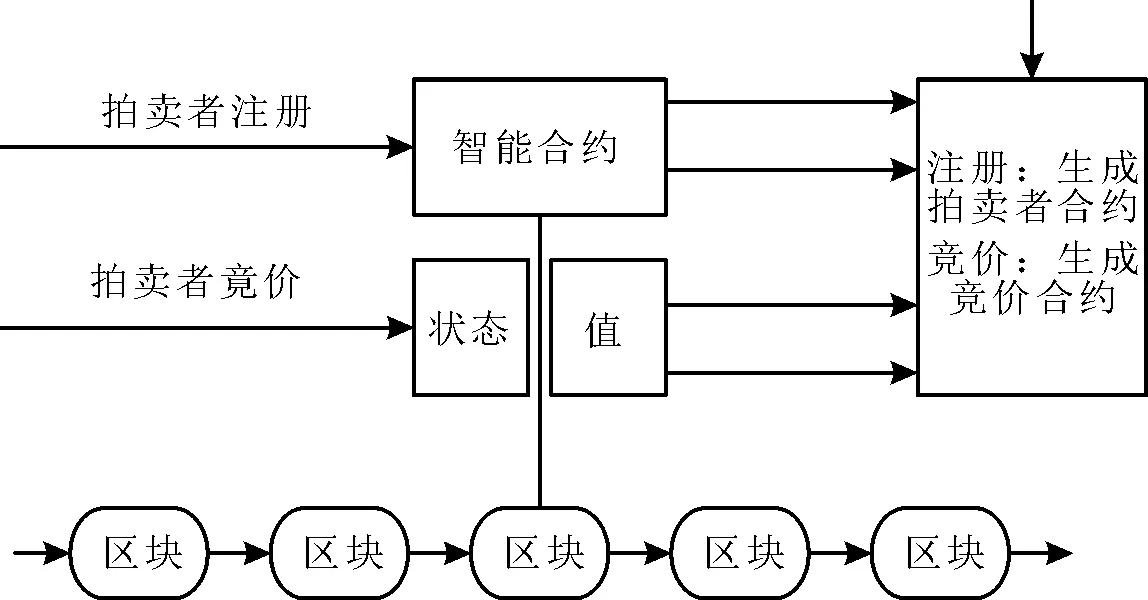
图1 智能合约在拍卖系统中的运作机制

2 基于身份的盲签名方案

W=

其中：Ppub=qG为用户公钥；a,b∈E(Fq)，用于确定椭圆曲线方程

y2=x3+ax+b,q>3
y2+xy=x3+ax2+b,q=2

基于身份的盲签名方案包括密钥生成、签名和验证等3个部分。

2.1 密钥生成

签名者私钥SI=qQI，QI=M(I)，将SI通过安全信道发送给签名者。签名者收到SI后，验证SIG=QIPpub是否成立，若成立，则接受该私钥，否则，重新生成私钥。

2.2 签名

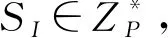
R+βG+γH+δQ=(x,y)

(1)

盲化后消息的计算表达式为

e=c-δ

(2)

c=M(m‖a‖I)

a=x(modp)

其中，(·‖·)表示两个比特串连接。

签名者对e进行签名

r=SI(1-e)

(3)

将签名r发送给用户，得到m的盲签名为(c,ρ,σ)，其中，ρ=r+β，σ=r+γ。

2.3 验证

任何第三方可以验证盲签名(c,ρ,σ)的正确性。验证等式为c=M[m‖I‖Rx(cQ+ρG+σH)(modp)]其中，Rx(·)表示x坐标的值。等式成立则接受签名，否则拒绝签名。验证过程如下。

cQ+ρG+σH=
cSI(G+H)+ρG+σH=
(cSI+ρ)G+(cSI+σ)H=
(cSI+r+β)G+(cSI+r+γ)H=
(cSI+SI-eSI+β)G+(cSI+SI-eSI+γ)H=
(δSI+SI+β)G+(δSI+SI+γ)H

而

R+βG+γH+δQ=
βG+γH+SI(G+H)+δSI(G+H)=
(β+SI+δSI)G+(γ+SI+δSI)H

因此

cQ+ρG+σH=R+βG+γH+δQ

盲签名(c,ρ,σ)验证成功。

3 电子拍卖系统

基于身份的盲签名方案，结合以太坊的智能合约，构建电子拍卖系统。基于身份的盲签名方案的引入为竞标者进行身份合法性认证授权，不仅保护竞标者隐私安全，还可有效防止外界攻击破坏匿名性。智能合约[22-23]分为竞标者管理合约与竞价管理合约。竞标组织者在区块链上发布竞标商品及竞标规则等，竞标者利用与自己身份有关的公钥和对应的私钥对竞标商品信息，标价加密给拍卖人，有出价最高者则成交商品。整个电子拍卖过程如图2所示。

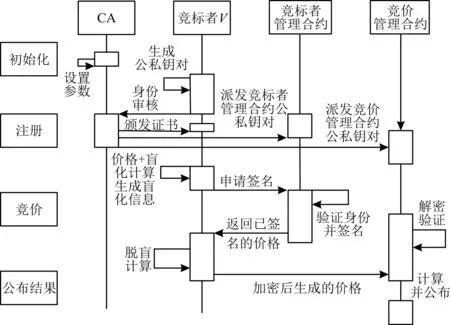
图2 电子拍卖过程

3.1 角色定义

电子拍卖系统主要包括竞标组织者、中央信任证书授权(Certificate Authority，CA)机构、竞标者管理合约和竞价管理合约等角色。

中央信任机构CA负责为合法竞标者颁发资格认证，生成基于身份的公私钥对的智能合约。竞标者管理合约自动审核竞标者身份的合法性，并参与标价盲签名，包括接受、签名和反馈。竞价管理合约自动选出收到的标价，并公布最高价。

3.2 竞拍者注册

竞拍者V向CA表明身份，等待CA对竞拍者的合法身份进行认证审核，若合格则颁发证书。同时，CA负责颁发基于竞拍者身份的公私钥对给智能合约。竞拍者注册的具体步骤如下。

步骤1竞拍者V生成基于身份的密钥SI，得到公钥R=SI(G+H)。

步骤2竞拍者V发送注册消息{R,I}给CA进行身份审核。

步骤3CA完成认证，若注册申请人V具有竞拍资格，则CA为其颁发资格证书C。

步骤4CA为拍卖者管理合约生成(SI,R)签名密钥对。私钥SI通过安全信道传递给竞拍者管理合约并保密。

步骤5竞拍者管理合约根据竞拍者注册情况生成竞拍者记录表。

步骤6CA为标价管理合约生成签名密钥对(SI,R)。同样，将私钥SI通过安全信道传递给标价管理合约并保密。

3.3 拍卖签名

竞拍者请求管理合约对竞拍价进行签名操作，具体步骤如下。

步骤1竞拍者V给出价格υ。

步骤3竞拍者管理合约利用式(3)对盲化价格进行签名计算，得到签名r。将竞拍者记录表中的C位置记录为“1”，并将r传回V。

3.4 竞价

竞拍者V对r进行解盲，获得原始价格签名信息，生成正式价格。正式价格需通过匿名加密方式发送给竞价管理合约，具体步骤如下。

步骤1竞拍者V根据ρ=r+β，σ=r+γ对r进行解盲，得到原始价格的盲签名(c,ρ,σ)。

步骤2竞拍者V将价格信息{(c,ρ,σ)‖υ}利用竞价管理合约公钥进行加密运算，生成正式价格

B=E{(c,ρ,σ)‖υ}

步骤3竞拍者V将正式价格B匿名发送给竞价管理合约。

3.5 公布

竞价合约收到V的B，利用私钥SI解密B，验证签名(c,ρ,σ)的有效性，即验证式(5)是否成立。若成立，接受签名(c,ρ,σ)，在竞拍者列表中查询c以防止复制攻击，若已有记录，则抛弃价格B。最终公布价格统计结果，并通过共识算法进行节点认证后记入区块链中。

4 安全性分析

4.1 不可伪造性分析

通过CA对竞拍者身份进行审核，保证了竞拍者群体身份的合法性。采用盲签名对价格信息加密，攻击者从竞拍者合约与竞价合约中窃取的信息{e,r,C}与{(ρ,σ),v}无法推断出关联性，且任何第三方都无法查看价格信息，保证了公平性。

攻击者选择(c,ρ,σ)冒充竞拍者V对价格v签名，则攻击者需要计算r=SI(1-e)，而攻击者不知道SI，则攻击者无法伪造竞拍者V对价格v的合法盲签名。

攻击者对价格的盲化由c=M(v‖a‖I)可知，攻击者在β,γ,δ未知情况下无法完成盲化。

攻击者对价格v的脱盲由ρ=r+β，σ=r+γ可知，攻击者在β,γ未知情况下无法进行c脱盲。

4.2 不可关联性分析

拍卖者V1和拍卖者V2提供价格v1和v2，与签名者合作完成签名运算，得到v1和v2的盲签名分别为(c1,ρ1,σ1)和(c2,ρ2,σ2)，则

c1=av1(modp)
c2=av2(modp)

若签名者猜测c1与v1对立，c2与v2对立，则

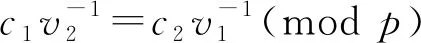
脱盲运算ρ=r+β，σ=r+γ无法判断签名者猜测ρ1、σ1、ρ2、σ2与r1、r2的对立关系是否正确，故每次签名更换盲因子β和γ，可确保被签名的消息对签名者的隐秘性。

竞价合约维护竞拍列表，防止复制攻击，竞价者列表与竞价列表使电子拍卖过程中具有不可伪造性。区块链智能合约设定运行的逻辑性代码，用户可以公开审查以确定其安全性，分布式结构也使得整个过程具有较强的鲁棒性。

4.3 效率分析

为了证实上述理论分析，在Inter(R) Core(TM) i5-8500 CPU @3.00 GHz，内存8 GB，Windows 10操作系统，JPBC代码库的仿真环境下，对所提方案进行仿真实验。所提方案密钥生成时间为2.65 ms，签名时间为2.37 ms，验证时间为2.62 ms。

所提方案与文献[24]方案、文献[25]方案、文献[26]方案和文献[27]方案等5种方案在计算次数为0～100的运行时间对比，如图3所示。可以看出，在任何计算次数下，所提方案的运行时都比其他方案有所提高。

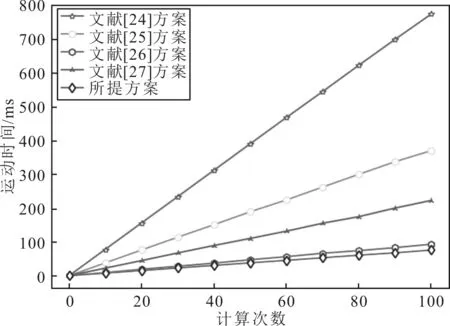
图3 不同方案运行时间对比

不同方案计算次数柱状图如图4所示，可以看出，所提方案与其他方案相比，计算次数有所减少。对比上述5种方案的特性，结果如表1所示。可以看出，所提方案同时具有安全性、公平性和身份合法性，优于其他4种方案。

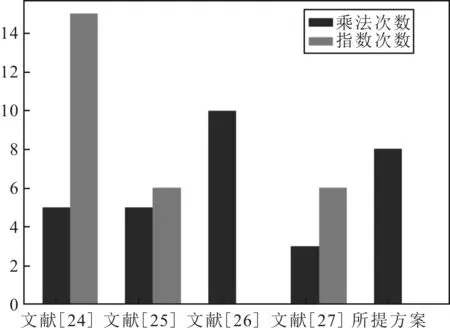
图4 不同方案计算次数对比

表1 特性比较

所提方案的计算开销主要来自盲签名的乘法和指数运算。定义盲签名过程的乘法运算为M，幂乘运算为E，不同方案的计算开销对比如表2所示。

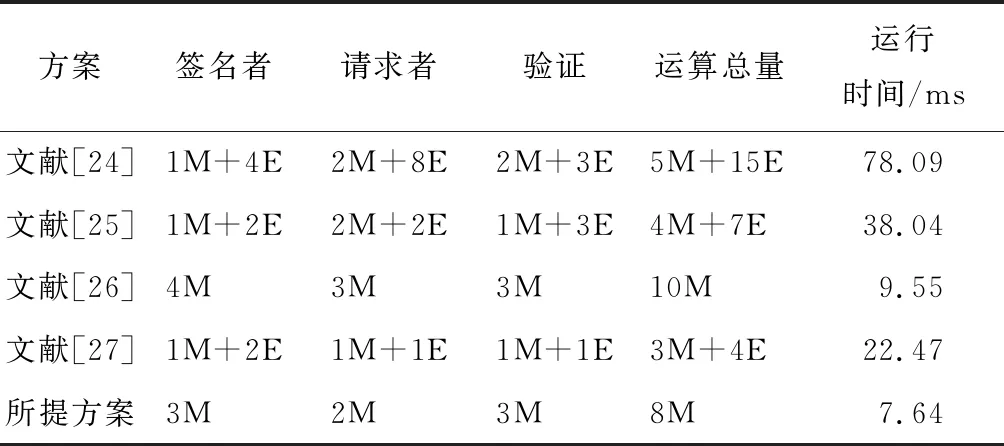
表2 计算开销

从表2中可以看出，所提方案只用了8次乘法运算，减少了指数和乘法运算，比其他方案计算速度更快、运行时间更短、效率更高。

区块链技术使得所提方案具有安全性和公平性，基于身份的盲签名使得所提方案具有身份合法性。因此，所提方案更适合电子拍卖。

5 结语

在电子拍卖系统中，加入了基于身份的盲签名和区块链技术，加强了电子拍卖中身份信息的隐蔽，改善了复杂的证书管理问题，同时，降低拍卖成本，减少了信任依赖。安全性分析结果表明所提方案具有安全性、公平性和身份合法性，且运算速度快，同时也验证了区块链技术在电子拍卖系统领域的适用性。