频率随机捷变雷达抗扫频干扰性能仿真
2021-11-10鲍秋香
鲍秋香
(中国船舶重工集团公司第七二三研究所,江苏 扬州 225101)
0 引 言
近年来,随着微波半导体技术、大规模集成电路技术和高速数字信号处理技术的发展,各种新体制雷达不断涌现,雷达技术得到了广泛的应用和迅速的发展[1-3]。雷达是现代战争中的“千里眼”,具有全天时、全天候的特点,是实现精确打击的必要手段和武器系统的测试评估手段,提高雷达的战场生存能力和对抗性决定了现代雷达技术的发展方向[4-5]。频率捷变雷达凭借其优越的抗干扰性能[6-7],受到了世界科研人员的广泛关注。
从目前的研究来看,针对频率捷变雷达的干扰主要为扫频干扰,扫频干扰兼备了窄带瞄准式干扰和宽带阻塞式干扰的特点,通过动态扫描干扰频带提高了干扰的功率利用率。程彦杰等人[8]分析了多种干扰样式对频率捷变雷达的干扰概率,但缺乏对频率捷变雷达在不同干扰样式下的抗干扰效能仿真。陈荣[9]对捷变雷达的信号特征进行了分析研究,但缺乏抗干扰效能的仿真研究。孙鹏[10]等人对自适应捷变频雷达的抗干扰性能进行分析,但缺乏抗干扰效能的仿真研究。
针对上述研究的不足,本文开展了频率随机捷变雷达抗扫频干扰性能仿真研究,首先建模研究频率随机捷变雷达的信号模型,然后对扫频干扰的数学模型进行理论分析,最后进行数值仿真。
1 频率随机捷变雷达数学模型
频率捷变[11]是雷达反侦察、抗干扰的重要手段。频率随机捷变雷达的脉冲序列是由一串载频在一定范围内随机跳变的全相参脉冲组成:
(1)
式中:fi=f0+m(i)Δf,为第i个脉冲的载频,m(i)为N个数随机排列的第i+1个值,N∈[0,N-1];Δf为最小跳频间隔。
目标回波可表示为:
(2)
其载频随时间的变化关系如图1所示。
回波信号与exp(-j2πfit)混频得到基带复信号为:
(3)
可以看出,脉间跳频脉冲序列回波混频以后的信号与各脉冲的载频有关。
2 扫频干扰数学模型
扫频干扰[12]按照频率步进产生干扰信号,使得干扰信号能量可以集中在每个扫频频点。
(4)
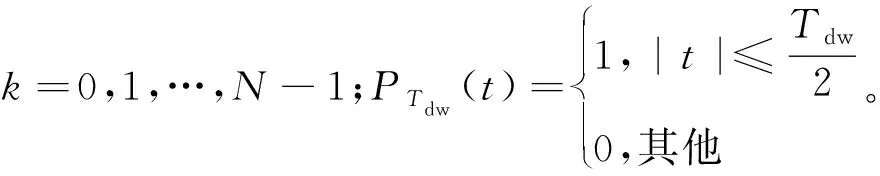
扫频干扰信号相位表示为:
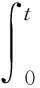
(5)
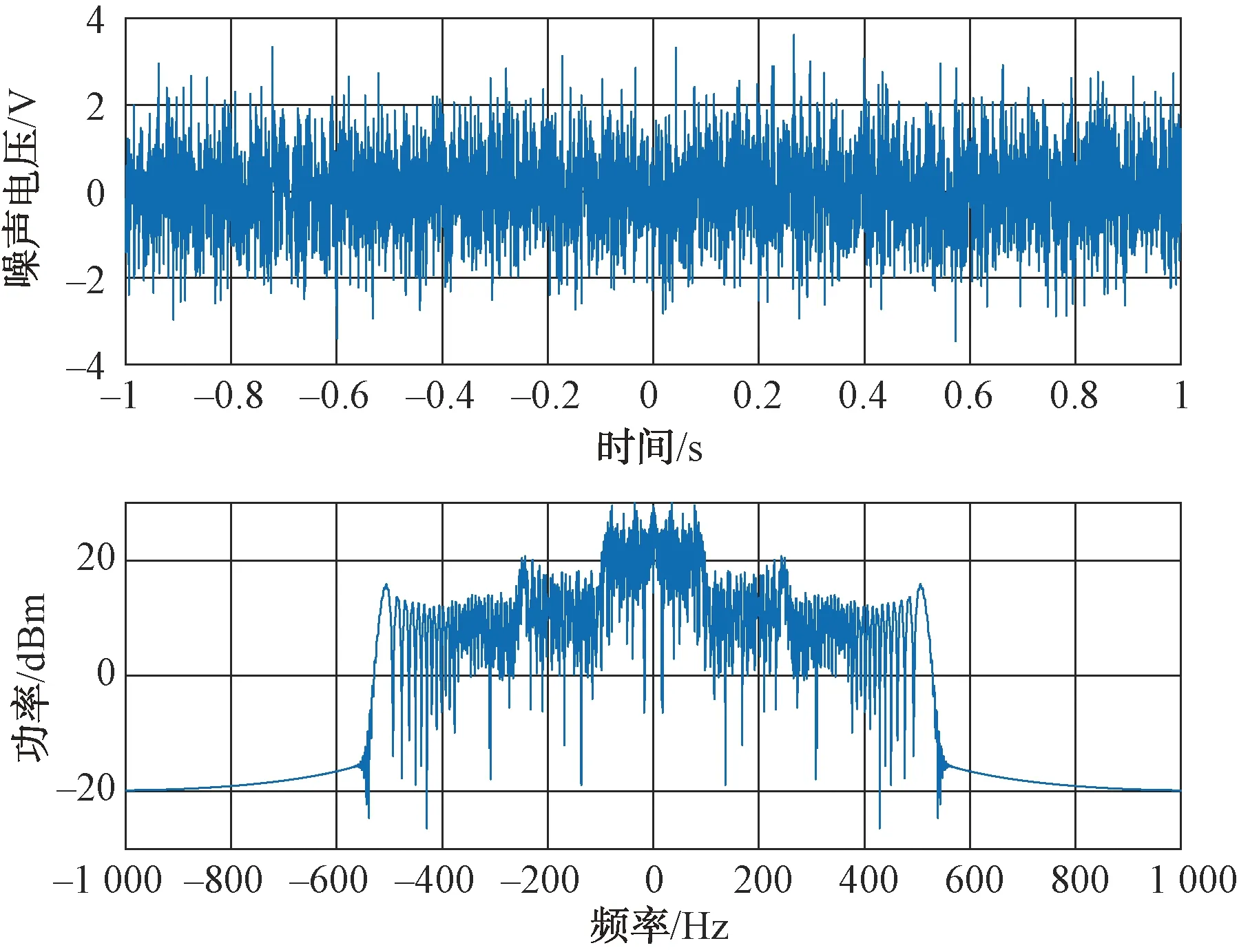
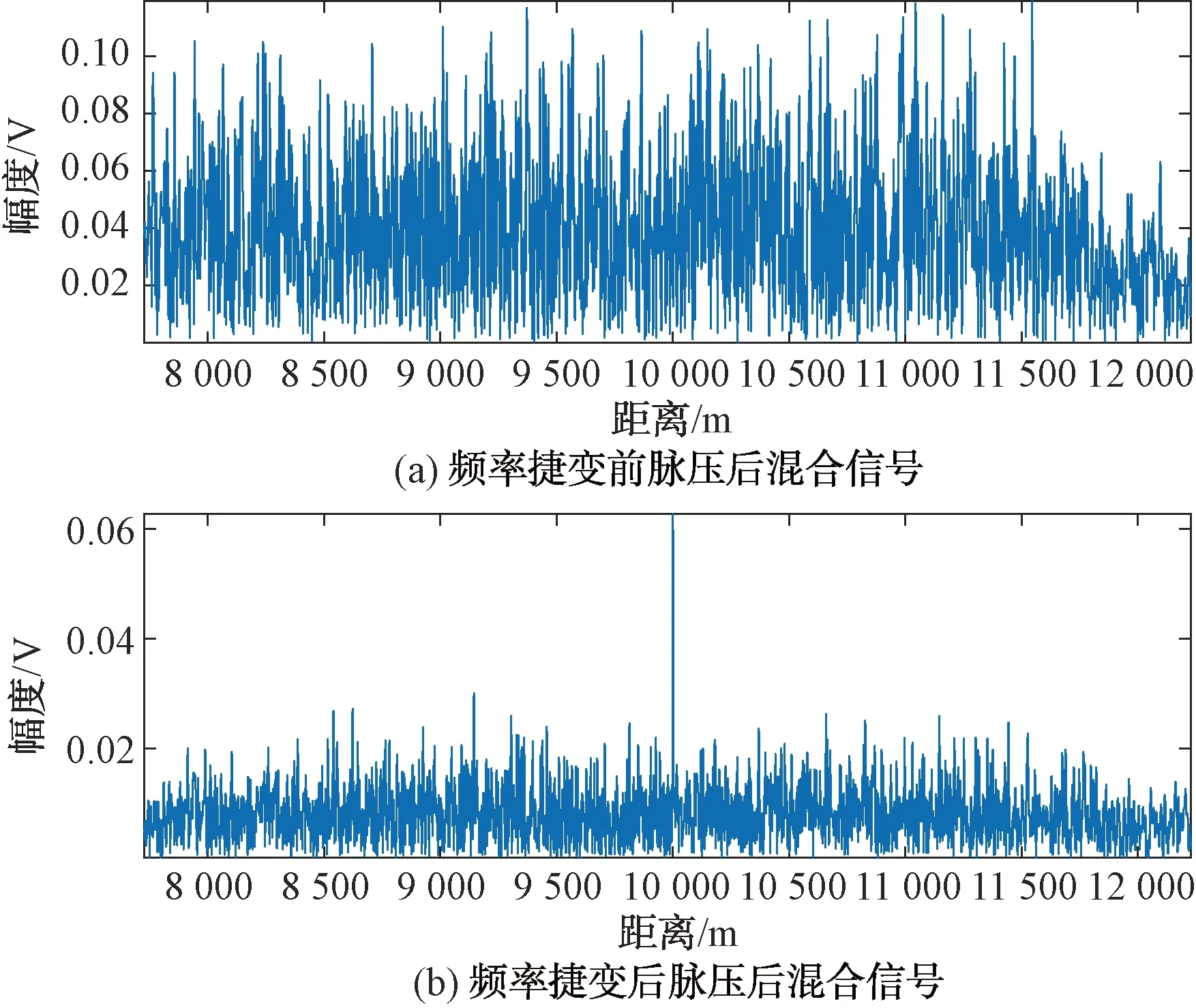
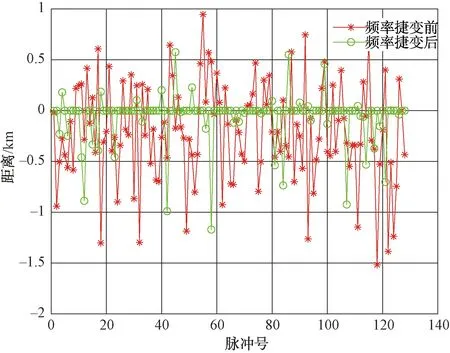
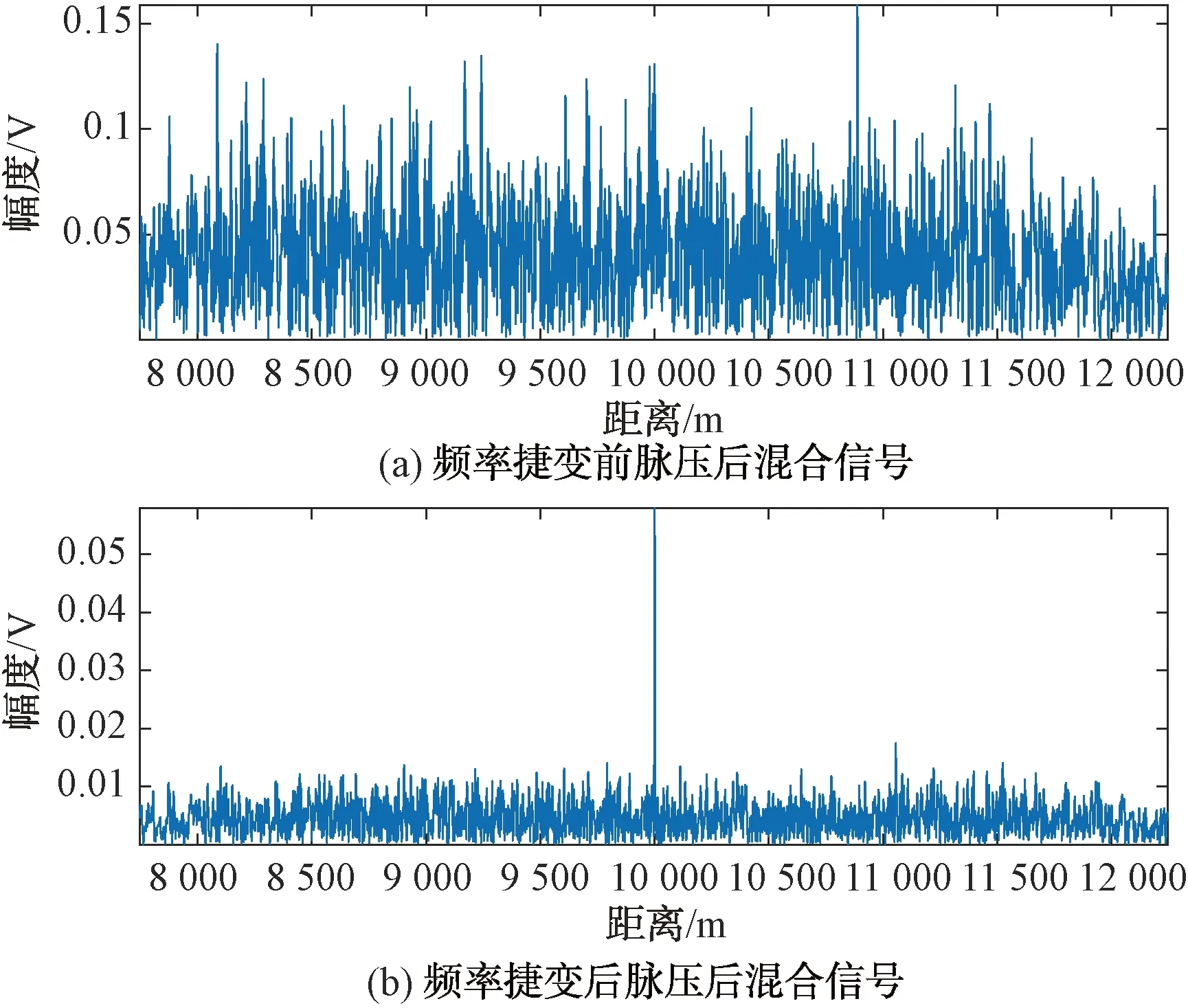
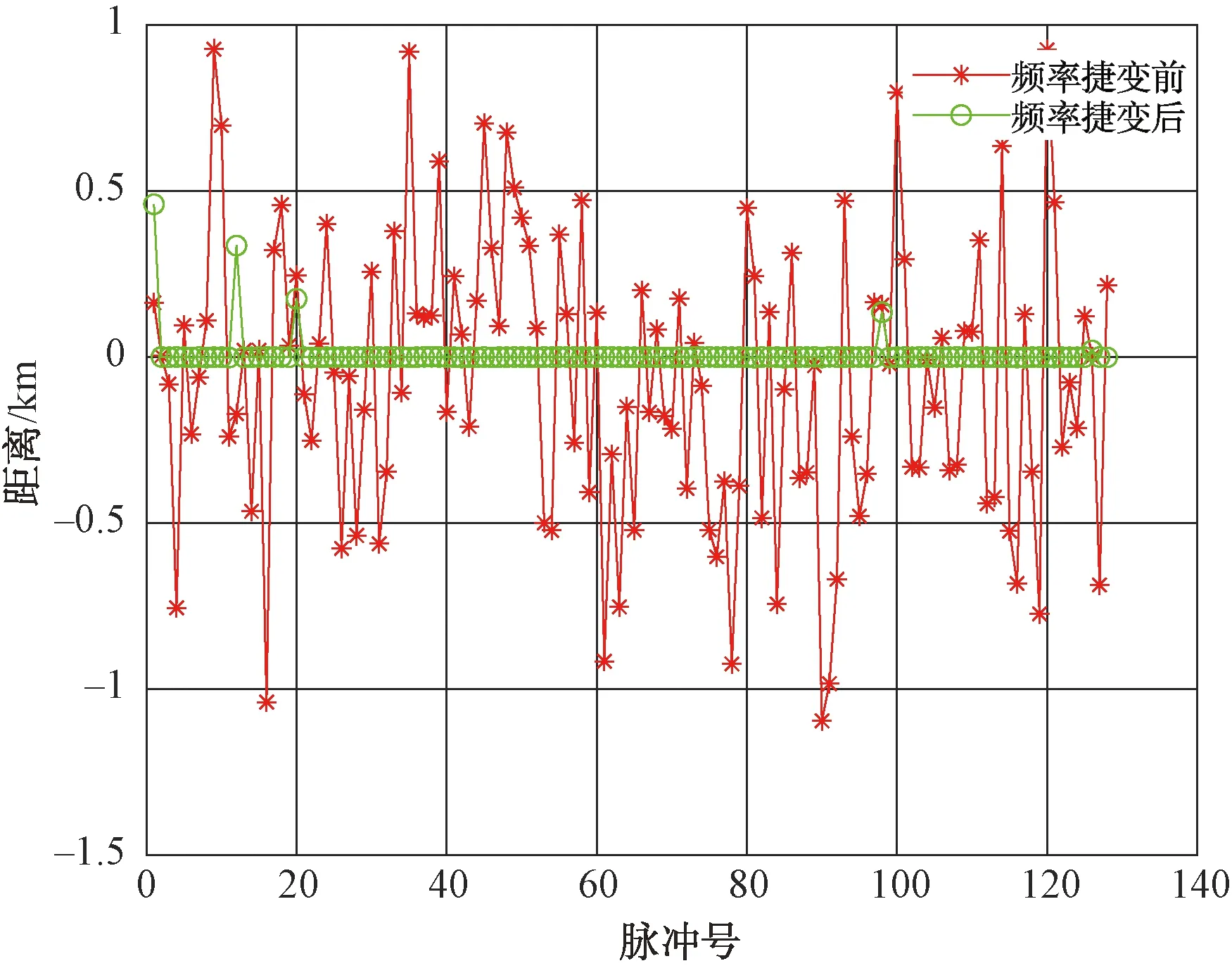
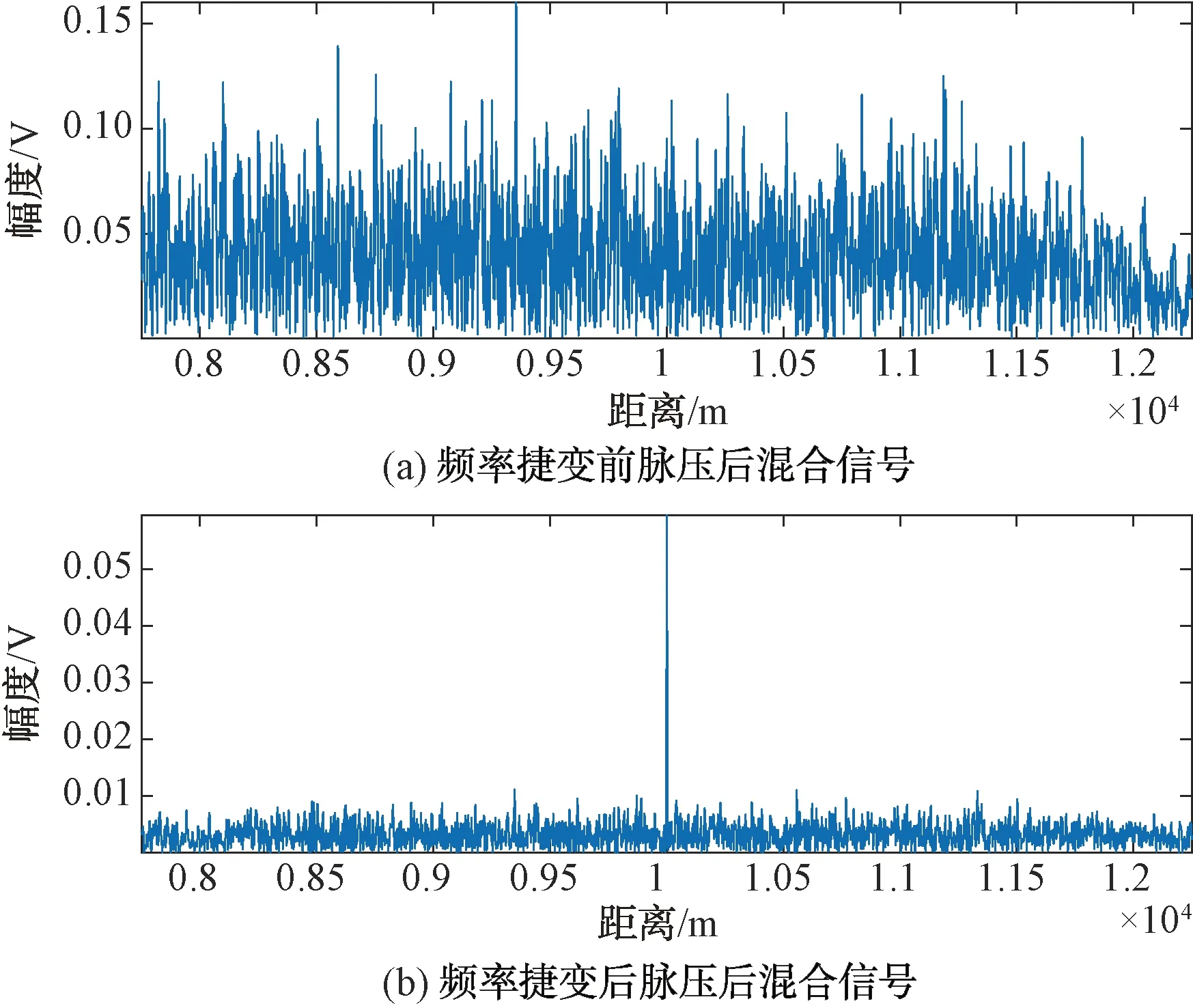
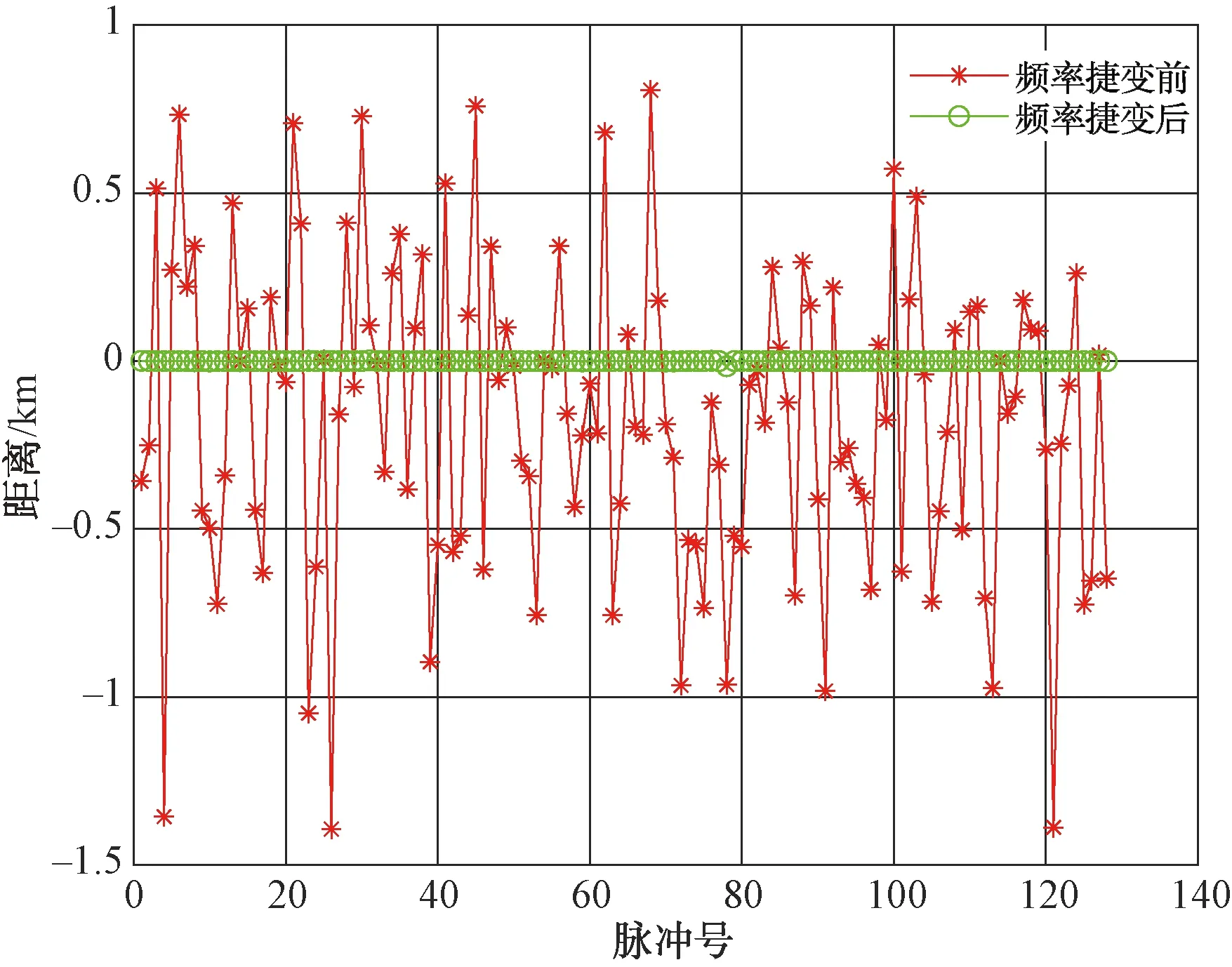
式中:kTdw 扫频干扰一般采用噪声调频方式,其表达式为: (6) 式中:Uj为噪声调频信号的幅度;fj为载频;Kf为调频斜率,且为常数;φ为初始相位。 噪声调频干扰的瞬时频率随调制噪声un(t)的幅度变化而变化,瞬时频率为: f(t)=fj+Kfun(t) (7) 干扰信号的频谱为: (8) 从上式求得干扰信号的谱宽为: Δfj=2(2ln2)1/2Kfσn (9) 扫频式干扰一般满足:Δfj=(2-5)Δfr,fs=fj(t),t∈[0,T]。 fs是干扰的中心频率为连续、以T为周期的函数。噪声调频干扰时域和频域分布如图2所示。 图2 噪声调频干扰时域和频域分布 根据上面描述的理论模型进行仿真,其中参数选择为:载频10 GHz,信号带宽80 MHz,脉宽20 μs,目标初始距离10 km,相参脉冲数128个,干扰信号为扫频式干扰,干扰扫频带宽为160 MHz。当频率捷变系数为1,也即频率捷变范围等于雷达带宽时,频率捷变抗干扰前后脉压的输出如图3所示。 图3 频率捷变抗干扰前后脉压的输出 由图3可以看出,当存在扫频干扰时,在采用频率捷变抗干扰前,经过脉压处理后,10 km处的目标被淹没在噪声干扰下;当采用频率捷变系数为1的频率捷变后,目标在10 km处得到凸显。图4为128个脉冲在采用频率捷变抗干扰前后的距离测量误差曲线。 图4 频率捷变抗干扰前后距离测量误差曲线 由图4可以看出,在采用频率捷变抗干扰前雷达的距离误差非常大,且呈现出杂乱分布,最大距离误差约1 500 m;而采用频率捷变抗干扰后,距离测量误差整体变小,最大为1 200 m。 当频率捷变系数为2,即频率捷变范围等于2倍雷达带宽时,频率捷变抗干扰前后脉压的输出和距离测量误差曲线如图5和图6所示。 图5 频率捷变抗干扰前后脉压的输出 图6 频率捷变抗干扰前后距离测量误差曲线 由图5和图6可以看出,当频率捷变系数增大为2时,采用频率捷变抗干扰后,距离测量误差整体变小,最大为500 m,而且只有4个脉冲存在明显的距离误差,其他脉冲距离误差较小。 当频率捷变系数为3,即频率捷变范围等于3倍雷达带宽时,频率捷变抗干扰前后脉压的输出和距离测量误差曲线如图7和图8所示。 图7 频率捷变抗干扰前后脉压的输出 图8 频率捷变抗干扰前后距离测量误差曲线 由图7和图8可以看出,当频率捷变系数增大为3时,采用频率捷变抗干扰后,距离测量误差变得非常小,不存在明显的距离误差。 本文针对雷达抗扫频干扰的问题开展基于频率随机捷变的雷达抗干扰研究,首先建立了频率随机捷变雷达的信号模型,然后对扫频干扰的数学模型进行理论分析,最后仿真研究了该方法的抗干扰性能。仿真结果表明,增大频率捷变系数可降低距离测量误差,获得非常好的跟踪性能,因此可以取得很好的抗干扰性能。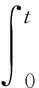
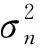
3 仿真验证
4 结束语
