基于LBM 的铝微滴斜柱沉积水平偏移研究1)

任彦霖 刘赵淼,†,2) 逄 燕,† 王 翔

*(北京工业大学材料与制造学部,北京 100124)

†(北京工业大学先进制造重点实验室,北京 100124)

引言

在传统增材制造技术中,微管结构[1-2]、多孔结构[3-4]因支撑材料难以去除而无法生产.金属液滴沉积制造技术基于逐点成型原理,通过按需喷射方式[5-6],进行无支撑斜柱沉积[7],实现空间网络结构的生产[8-9].铝液滴是增材制造技术中常用的工质,具有较好的界面张力和黏度等材料特性,被广泛应用于液滴沉积制造技术的研究中[10-11].然而,先沉积液滴非受限表面凝固后的球帽形貌会影响后沉积液滴运动行为,使液滴实际沉积位置与其生成位置存在偏差.这种偏差使液滴沉积行为产生的偏移距离,会降低斜柱沉积形貌精度.精确分析影响水平偏移程度的控制因素,成为斜柱沉积过程亟待解决的关键问题.

沉积液滴在球帽形凝固表面上的运动过程,是一个复杂的流动、传热过程,其实际沉积位置受到冲击[12]、震荡[13]、共同凝固过程[14]等因素影响.Zhang等[7]在液滴连续沉积实验中,通过调整融合率引起实际沉积位置偏移,并影响斜柱倾角;进一步固定融合率,却依然存在沉积位置偏移,影响倾角的控制精度[15].Graham 等[16]和Dalili 等[17]实验观测了水滴的相互融合过程,表明沉积位置的偏移由界面张力作用引起.Li 等[18]探究了石蜡滴水平连续沉积过程,发现液滴间距会影响位置偏移程度.这些研究多集中于液滴融合过程产生的偏移运动,而缺少金属液滴凝固形成的球帽结构对偏移运动的影响.Ju 等[19]研究了液滴在球面上的沉积运动,表明球面曲率影响液滴沉积运动,但由于液滴与球面同轴,而未产生滑落.Tian 等[20]实验研究了液滴在倾斜表面的沉积过程,提出了沉积液滴动力学行为的能量分析法.对于铝液滴在球帽形凝固表面上的偏移运动过程,前、后液滴间轴线距离的影响及其受力机理尚未明确,对斜柱沉积过程参数的优化设计有待研究.

为分析偏移运动和受力机理,铝液滴的连续沉积过程需要采用格子玻尔兹曼方法(LBM),进行数值模拟研究.LBM 是一种介观尺度的模拟算法,在两相流动方面采用S-C 伪势模型统一处理离散相和分散相[21],并引入C-S 状态方程计算分子碰撞有效质量使其满足热力学一致性[22],对平衡速度进行修正[23];在传热相变方面采用焓的显式法求解传热过程,通过双分布方程使其与流动耦合[24],并对固液相变前沿进行无滑移边界处理[25-26].LBM 已经具备解决实际工程中传热、相变问题的能力[27-31],并应用于单液滴沉积过程的研究中[32-34],有助于实现金属液滴连续沉积过程的建模.

本文将基于LBM 建立铝液滴斜柱沉积模型,采用自编程序研究液滴水平偏移过程和受力机理.根据液滴能量演化趋势,对沉积过程进行阶段划分.结合质心位移曲线,分析水平偏移产生的主要阶段和主要推动力.根据偏移距离的演化规律,对扫描步距进行优化,以实现斜柱的均匀沉积和倾角的精确控制.

1 物理模型

斜柱沉积制造是多个液滴按相同间距连续沉积的过程,以其中两液滴先后下落的物理过程,作为主要研究对象.如图1 所示,密度、初始焓、直径分别为ρH,HA,Dd的两个铝液滴,从同一高度h,水平相距L的位置先后下落.先沉积的液滴接触温度为TB的恒温基板后凝固,后沉积的液滴接触前者表面后凝固.外界环境气体密度为ρ0,初始温度为T0(T0=TB).铝液滴材料参数如表1 所示.

图1 多液滴沉积物理过程简图Fig.1 Physical process of multi-droplet deposition

表1 铝液滴材料参数Table 1 Material properties of the aluminum droplets

2 数值方法

2.1 两相流动方程

液滴沉积过程是一个两相流动过程,需要准确追踪气液界面.本文采用伪势模型,通过流体粒子间相互作用力,使其自发地形成两相界面,以满足热力学一致性和第一性原理.首先对流动过程建立密度的格子玻尔兹曼方程

式中,i表示格子方向的索引编号,ei表示i方向上的单位格子速度,τf表示密度松弛时间[35].浸没边界法是LBM 中处理曲面边界的常用方法[36].本文采用Noble 等[26]提出的方法处理相变界面,以B表示固体边界判别函数,表示附加碰撞项.

在流动方程的基础上,引入相邻位点间粒子的长程相互作用力,实现流体的两相分离

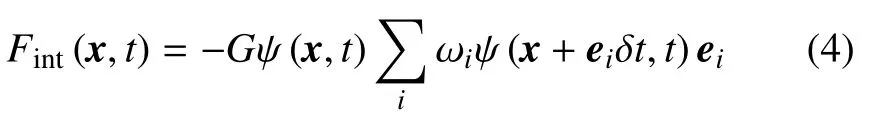
式中,G表示相互作用强度,ψ 表示碰撞有效质量.为了保证两相分离状态具有热力学一致性,碰撞有效质量通过C-S 状态方程计算[22]

在流固界面上,近壁面粒子所受作用力为

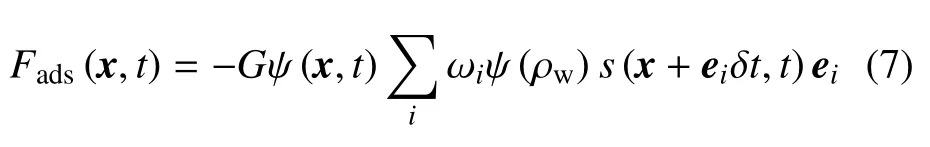
式中,ρw表示壁面粒子假想密度,用于调节固液表面浸润度.采用Shan-Doolen 平衡态分布函数的速度校正法,对平衡速度和物理速度进行修正[23]

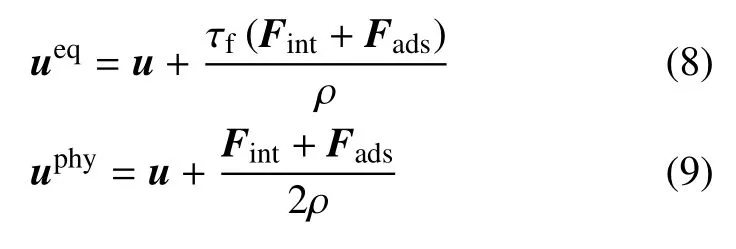
2.2 传热相变方程

液滴在沉积过程中传热并发生凝固,需要引入焓的格子玻尔兹曼方程求解

式中,τg表示焓的松弛时间,表示焓的平衡分布函数,并采用Huang 等[34]提出的显式方程表示

式中,ωi表示i方向上的加权,cs表示格子声速,Cp表示定压热容.根据流体焓不仅可以计算出当地温度,还可以追踪固液相变界面

式中,HS表示流体固化焓,HL表示流体液化焓,TS表示固相线,TL表示液相线.对于相变界面上的无滑移边界条件,采用Noble 等[26]提出的移动固体边界处理方法,并通过固体判别函数和附加碰撞项修正流动方程

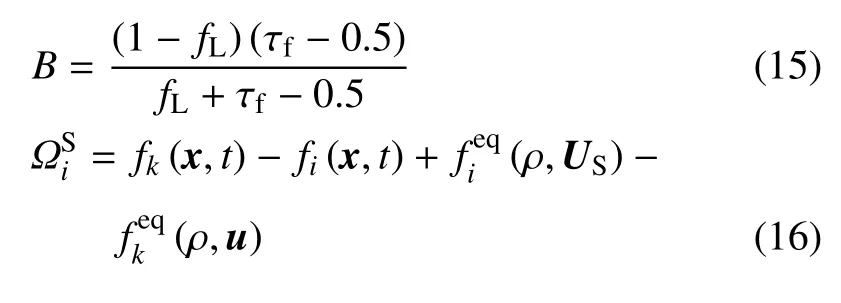
式中,k表示运动方向与ei相反的分布函数索引,US表示固体的运动速度.

2.3 网格独立性验证

通过模拟单液滴下落过程中的形心高度变化,对模型进行网格独立性验证.计算域上下表面设为半步反弹及恒温边界条件,四周设置为循环边界条件,模拟单液滴下落过程.如图2 所示,当液滴直径为Dd=36 lu 时,计算域总网格量超过7.9×105个单元,液滴形心运动趋势不再有明显变化.在LBM中,计算域在无特殊格式处理时,通常采用均匀网格划分,网格精度由宏观尺寸在格子上的分辨率体现.根据液滴实际直径Dd=0.6 mm,和网格独立性验证得到的网格量大小,得到宏观空间尺度的国际单位分辨率为1 m=6.0×104lu,并在保证计算收敛性的基础上,进一步确定时间、温度、质量等基本单位在格子上的分辨率(如表2 所示).

图2 网格独立性验证Fig.2 Grid independence verification

表2 国际基本单位与格子单位的换算关系Table 2 Relationship between the SI units and the lattice units

3 结果与讨论

对水平偏移距离的准确控制,需要根据液滴沉积过程中的能量变化,对液滴运动过程进行划分,探寻水平偏移的主要产生阶段和主要推动力.

3.1 能量演化及运动阶段划分

沉积液滴与环境气体、凝固液滴形成三相接触,其表面能直接反应液滴形态变化和运动过程.Tian等[20]根据表面能的充放过程,对液滴运动过程进行阶段划分,并建立了表面能计算公式

式中,Sgl表示气液界面面积,Sls表示固液界面面积,θe表示液滴静态接触角.沉积液滴除了表面能外,还具有重力势能GP和动能KE,这两种能量的计算模型分别表示为

式中,ρ 表示流体微元密度,g表示重力加速度,Δz表示流体微元运动的相对高度,u表示流体微元速度.沉积液滴接触凝固表面后,由于壁面剪切作用产生黏性耗散VD,使表面能、重力势能与动能之和降低.因此,液滴沉积过程中产生的黏性耗散可推算为

图3 提取了浸润度为ξ=0.42、两液滴轴线距离为L*=0.33 下的液滴沉积能量变化.其中Fo是无量纲时间尺度,表示为

式中,υ 是铝的运动黏度,t表示时间,Dd为液滴的特征长度,取液滴的初始直径.根据SE的充放变化,可以将沉积液滴运动过程分为下落阶段、快速扩张阶段、慢速扩张阶段、回弹阶段[37](如图3).在下落阶段(Fo＜0.17),液滴在界面张力作用下维持球状,SE不发生明显改变.重力作用使势能下降|ΔGP|=2.32 mu·lu2/ts2,并等额转化为动能KE,形成接触凝固表面前的冲击速度.

图3 后沉积液滴运动过程中的能量演化曲线Fig.3 Tendency of energy in the motion of deposit droplet

液滴接触凝固表面后,与气体、凝固表面形成三相接触,进入快速扩张阶段(0.17 ＜Fo≤0.22).表面能降低|ΔS E|=9.77 mu·lu2/ts2,重力势能减小|ΔGP|=3.23 mu·lu2/ts2,表明毛细力和重力在快速扩张运动中起推动作用.此时液滴中央截面状态如图3(b) 所示,毛细力带动接触线扩张,并使液滴质心下降.过流断面的减小使黏性剪切作用增强,使黏性耗散增大|ΔVD|=13.01 mu·lu2/ts2,动能减小|ΔKE|=0.01 mu·lu2/ts2.

在慢速扩张阶段中(0.22 ＜Fo≤0.28).表面能增大|ΔS E|=3.09 mu·lu2/ts2,重力势能降低|ΔGP|=0.94 mu·lu2/ts2.该结果表明毛细力在慢速扩张过程中起阻碍作用,而重力起推动作用.慢速扩张阶段的初始状态如图3(c) 所示,接触线达到毛细平衡状态,并开始在重力和流动惯性作用下受迫扩张.流速因气液界面阻碍而降低,使壁面剪切强度降低,黏性耗散仅为|ΔVD|=0.91 mu·lu2/ts2,同时动能降低|ΔKE|=3.06 mu·lu2/ts2.

进入回弹阶段后 (Fo＞ 0.28),表面能下降|ΔS E|=4.44 mu·lu2/ts2,同时重力势能提高|ΔGP|=0.13 mu·lu2/ts2,表明毛细力在接触线回弹过程中起推动作用、重力起阻碍作用,但二者作用效果均低于快速扩张阶段.此时液滴中央截面状态如图3(d)所示,毛细力带动接触线回缩,并使质心位置升高.过流断面的增大和流速的减小使黏性耗散增大|ΔVD|=4.43 mu·lu2/ts2,并使动能降低|ΔKE|=0.12 mu·lu2/ts2.

尽管毛细力在扩张运动中,先后起到推动作用和抑制作用,但由于流动形式相似,所以下文被统称为扩张阶段.图4(a) 表明扩张阶段中液滴内部流场以惯性力主导的下落运动为主,而凝固表面上的流场表现为扩散运动.如图4(b)所示的回弹阶段中,上游接触点切线倾角较小,重力与毛细力同向,促使接触线进行回弹运动;下游接触点切线倾角较大,重力与毛细力反向,反而使接触线继续向下游运动.由此导致液滴整体向下游运动,形成了滚动流动状态.

图4 扩张和回弹阶段中的流场形式Fig.4 The flow field in spreading and rebound stage

由于前沉积液滴的凝固表面具有轴对称的球面形貌,使后沉积液滴在各方向上的运动相同.为分析水平偏移运动过程,后文以偏移方向作为水平x轴正方向,并提取三维结果中液滴质心运动距离和速度进行分析.

3.2 水平偏移主要阶段及推动力

图5 展示了两液滴轴线距离为L*=0.33 的偏移运动过程.其中L*和δL*分别为无量纲轴线间距和无量纲偏移距离,表示为

图5 冲击液滴偏移过程Fig.5 Horizontal displacements of the deposit droplets

是液滴形心在水平方向的无量纲偏移速度

沉积液滴在扩张阶段中发生加速偏移,并在Fo=0.29 时偏移速度达到峰值=1.32,而偏移距离仅为δL*=0.05.在随后的回弹阶段中,偏移运动开始减速,在Fo=0.52 时偏移速度降低至=0.06,偏移距离增大至δL*=0.21.由此可见,水平偏移运动主要发生在回弹阶段,而加速过程发生在扩张阶段.根据3.1 节对扩张阶段的受力分析,表明重力、毛细力是水平偏移运动的主要推动力.

3.3 扫描步距优化

为实现对偏移距离的准确控制,需要在实际工况中,选择与主要推动力对应的控制条件,并对其影响程度进行标定.

铝液滴与气体、凝固表面形成的三相接触过程中,固液界面浸润度是控制毛细力作用的主要参数.液滴间轴线距离决定了两液滴的接触点位置,而在半球形凝固表面上,接触点的位置与该点切线斜率直接相关,并决定了切线方向上的重力分量.液滴轴线距离和固液界面浸润度成为本文偏移距离研究的主要控制参数.

如图6 所示,水平偏移距离随轴线距离的演化趋势呈现阶段化特性:L*＜0.10 时,偏移距离随着轴线距离的增大而增大;而L*＞0.10 后,偏移距离随着轴线距离的增大而减小.在不同固液浸润度条件下对比,表明偏移程度随着浸润度的增大而减小,并且不影响偏移程度随轴线距离的演化趋势.由于固液浸润度是材料属性,需要根据材料浸润度以及所需的偏移距离δL,选择对应的轴线距离L.以浸润度为ξ=0.42 的材料工况为例,对偏移距离进行数据拟合得到对勾函数关系

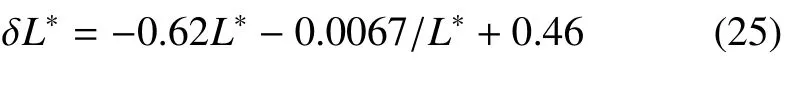
图6 液滴间轴线距离对水平偏移距离的影响Fig.6 Influence of axes distance between droplets on the horizontal deviation

偏移程度随轴线间距演化的阶段化特征,表明液滴的偏移运动过程存在竞争机制.图7 对比了不同轴线距离下,液滴水平偏移速度的演化趋势:在接触凝固表面后开始加速,进入回弹阶段后减速,并在表面能完全释放后速度趋于平缓.演化趋势差异,体现在加速段时长和速度极大值的变化.

如图7 所示,随着轴线间距由L*=0.03 增大到L*=0.14,速度极大值从=0.66 增大到=1.44,随后小幅减小.液滴接触凝固表面后(Fo＞Fo0),速度达到极大值前的加速段时长Foa=Fo-Fo0,随倾角的增大而缩短.随着轴线间距由L*=0.03 增大到L*=0.33,加速段时长从Foa=0.25 减小到Foa=0.17.对速度极大值和加速段时长的模拟结果进行数据拟合,得到与轴线间距的关系式

图7 轴线间距对偏移运动的影响Fig.7 Influence of axis distance on deviate movement

该结果表明加速段时长与轴线间距呈单调减小关系,而速度极大值随轴线间距先增大后小幅减小.二者对偏移程度起着相反的作用:加速段时长的缩短会提高偏移程度,而速度极大值的增大则与之相反.这种竞争关系是导致偏移程度随轴线间距表现出阶段化特征的根本原因.

作为液滴沉积的控制参数之一,沉积高度的增大会提高冲击速度,也会使液滴温度提早降低,所以该工况的研究范围被控制在h*=1.67～2.00 内.图8展示了h*=1.67,1.72,1.83 三组工况的对比结果,表明偏移程度随轴线间距具有相似的演化趋势,最大偏移距离与沉积高度负相关,分别为δL*=0.41,0.38,0.35.这是由于液滴接触凝固表面时,内部流体以凝固表面上的扩散运动为主,冲击速度的增大使流体克服重力作用产生的流量分配差异,使液滴在扩张阶段中的偏移距离和速度减小.该结果表明,沉积高度的增大对偏移程度起抑制作用.

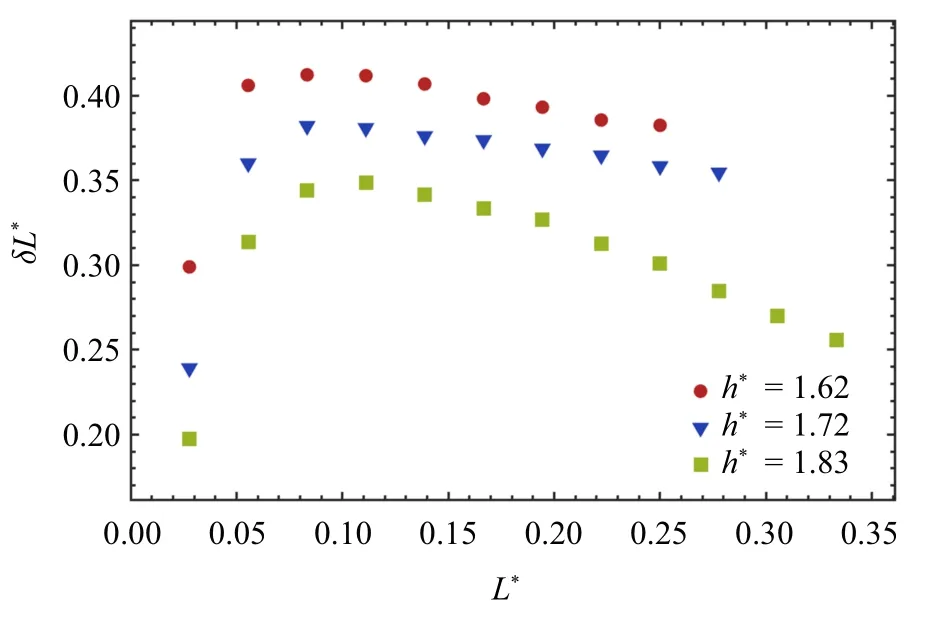
图8 轴线间距对水平偏移程度的影响Fig.8 Influence of axial distance on horizontal deviation

为实现斜柱的均匀沉积,后续液滴沉积时的扫描步距既要包括液滴间的轴线距离,还要考虑前沉积液滴的偏移距离

在保证每个液滴扫描步距一致的基础上,根据Zhang 等[7]提出的斜柱倾角理论公式,可以得到

式中ε 表示液滴间的融合率,是沉积后的液滴间形心距离与初始直径之比.本文采用固液浸润度为ξ=0.42 的铝液滴,从高度为h*=1.5 下落.通过测量液滴形心间距,得到融合率为ε=0.63,并将其代入式(29)、与式(25)和式(28)联立,得到液滴轴线距离与倾角关系式为

如图9 所示,根据式(28) 计算得到扫描步距分别为w*=0.21,0.29,0.34,0.37 的工况下,多液滴斜柱沉积模拟结果具有均匀的形貌结构,并且倾角与理论结果一致[7].

图9 斜柱倾角与扫描步距关系及其沉积形貌Fig.9 Relationship between the tilt angle and the scanning step

4 结论

本文通过建立LBM 液滴连续沉积模型,探究了铝液滴沉积过程中水平偏移的主要发生阶段及其影响因素.液滴沉积运动从能量角度被分为下落、快速扩张、慢速扩张和回弹4 个阶段.扩张阶段是偏移加速运动的主要阶段,而回弹阶段产生了主要偏移距离.偏移运动主要推动力源于毛细力、重力和黏性剪切力在扩张阶段中的共同作用.此外,偏移距离随轴线距离演化趋势呈阶段化特性,拟合结果呈对勾函数关系.这种阶段化特性是偏移运动中加速段时长和速度极大值间的竞争关系导致.沉积高度和浸润度的减小均不影响该演化趋势,但会使偏移程度增大.结合斜柱几何特性,扫描步距与斜柱倾角的关系式得到建立.在该模型下选择扫描步距,进行的多液滴连续沉积模拟,具有均匀的斜柱形貌,并且倾角与理论结果吻合程度较好.本文所得结果有助于偏移距离的精确控制,提高斜柱沉积制造的形貌质量.