基于Proteus的光伏系统MPPT算法仿真研究

丁 艳，李佳明，高铄涵，袁隆基

(1.中国矿业大学徐海学院，江苏徐州221008；2.中国矿业大学电气与动力工程学院，江苏徐州221116）

在化石能源逐渐枯竭、环境问题日益突出的当今社会，太阳能以取之不尽、用之不竭、绿色环保的独特优势倍受人们青睐[1-4]。近些年来，太阳能光伏系统已被广泛应用到各行各业，但其应用中仍存在着效率低、成本高等一系列问题[5]。国内外众多专家学者对此展开研究，其中部分学者尝试通过一些仿真工具对太阳能光伏系统进行仿真分析，以寻求获得太阳能光伏系统的最大功率点，从而提高太阳能光伏板的利用效率。但大部分研究都停留在利用Matlab/Simulink 或PSIM 工具[6-12]对太阳能光伏系统进行仿真分析，仿真过程很难嵌入可编程的微处理器仿真（如：PIC，DSP，Arduino 或者FPGA 等等），不同的MPPT 算法仿真需搭建不同的仿真模型。为此，本文基于Proteus 仿真软件搭建了Arduino 可编程微处理器光伏系统MPPT 算法仿真平台，在相同的仿真电路里，仅需改变Arduino UNO 微处理器的程序，即可实现不同MPPT 算法的仿真研究，同时本文将此平台应用于传统电导增量法及其优化的仿真研究中，以便解决传统电导增量法响应慢、稳定性差的问题。

1 仿真电路

1.1 光伏阵列模型

考虑到建模精度和难易程度，本文采用最经典的光伏阵列的单二极管模型[13-16]，其等效电路如图1所示。

图1 光伏阵列等效电路

基于半导体理论，从数学上描述理想光伏阵列的I-V特性的基本方程为[13-16]：

式中：I为输出电流；Iph为光生电流；I0为二极管反向饱和电流；q为单位电荷量；V为输出电压；Rs为等效串联电阻；Rsh为等效并联电阻；Ns为二极管理想因子；K为玻尔兹曼常量；T为光伏阵列温度。

基于以上等效电路和基本方程，在Proteus 虚拟仿真软件里设计了光伏阵列仿真模型，如图2所示。

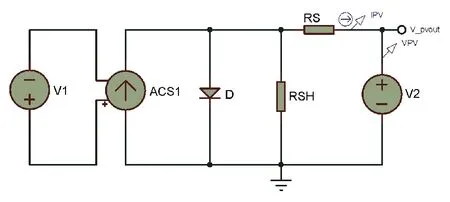
图2 光伏阵列仿真模型

图2 的Proteus 虚拟仿真模型中，ACS1 为压控电流源，V1为电压源，二者组成在一起共同模拟光电流IPh，采用直流电压源V2 模拟仿真负载。光伏阵列参数为：最大功率20 W；最佳电源电压18.76 V；最佳工作电流1.07 A；开路电压22.7 V；短路电流1.17 A；等效并联电阻405.96 Ω；等效串联电阻1.054 7 Ω。

1.2 仿真电路

该平台仿真电路包含了光伏阵列模型、DC/DC 转换电路、功率测试以及最大功率点跟踪算法，MPPT 算法主要是利用Arduino UNO 嵌入板采用内部编程的方式实现，整个电路如图3所示。

图3 太阳能光伏系统MPPT模拟仿真电路图

因为光伏系统的输出在0～22.7 V 之间，图3 中采用R2(100 kΩ)和R3(25 kΩ)对光伏阵列输出电压进行分压，得到0～5 V 范围内的电压信号，供UNO 主板A0 口采集。针对电流，在光伏阵列模型输出口串联一个阻值为0.1 Ω 的精密电阻，获取精密电阻两端电位差再通过减法运算放大器U3，得到放大10 倍的压差信号，供UNO 主板A1 口采集，然后进行相关编程处理，将光伏阵列模型的输出电压、输出电流和输出功率输出到LCD1602 液晶显示。UNO 主板PD6 口输出PWM信号通过TC4420 高速MOSFET 驱动器驱动场效应管Q1，获取合适的扰动量计算跟踪不同工况下的最大功率点。

2 MPPT 传统电导增量法及其优化

2.1 传统电导增量法

传统电导增量法[12]是以光伏阵列的输出功率P与电压V曲线的斜率（dP/dV）判断追踪的方向。当dP/dV>0，可见此时功率处于最大功率点的左侧；当dP/dV<0，可见此时功率处于最大功率点的右侧；当dP/dV=0，则此时功率正好是最大功率点的位置。因为P=V×I的关系，所以可得出下面式(2)的关系：

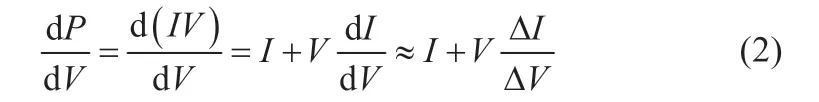
于是，dP/dV与0 的关系可以表达为ΔI/ΔV与-I/V的关系。当ΔI/ΔV=-I/V时，则正好是最大功率点位置；当ΔI/ΔV>-I/V时，说明此时输出功率处于最大功率点左侧；当ΔI/ΔV<-I/V时，说明此时输出功率处于最大功率点右侧。

在实际算法运算时，通常在占空比D上施加扰动定量Δd，计算出ΔV和ΔI。如果ΔV=0且ΔI=0，或者ΔI/ΔV=-I/V，则说明正好是最大功率点；如果ΔV=0 且ΔI>0，或者ΔI/ΔV>-I/V，则需要继续在相反方向上施加扰动Δd；如果ΔV=0且ΔI<0，或者ΔI/ΔV<-I/V，则需要在相同方向上施加扰动Δd；如此循环，最终获取最大功率点位置。传统电导增量算法流程图如图4所示。

图4 传统电导增量法流程图

2.2 电导增量法优化

在传统电导增量法中，步长较小(即扰动量Δd较小)，则跟踪时稳态性能较好但响应速度较慢；如果步长较大，则响应速度较快而稳定性能较差。为进一步权衡响应速度和稳定效果，将实时变化量ΔM作为变步长对电导增量算法进行优化升级：

式中：|ΔP|为实时变化的输出功率变化量；N为系数。

在远离最大功率点的位置，优先考虑的是响应速度，需要较大的步长，而此时刚好是输出功率变化量比较大；而在靠近最大功率点的位置，则优先考虑稳定性，需要较小的步长，此时输出功率变化量刚好比较小，所以算法中采用ΔM作为变步长更适合实际跟踪的需要。在此优化的基础上，为了提高微处理器的实时处理能力，对算法进行消除除法运算处理。由传统电导增量法可知：

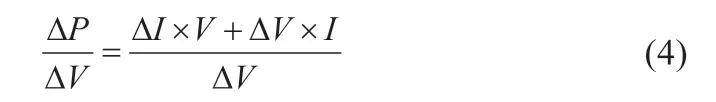
将传统电导增量法进行变换，当(ΔI×V+ΔV×I)/ΔV=0 时，为最大功率点位置；当(ΔI×V+ΔV×I)/ ΔV>0 时，此时输出功率处于最大功率点左侧；当(ΔI×V+ΔV×I)/ ΔV<0 时，此时输出功率处于最大功率点右侧。在Arduino UNO 的程序中采用“与”的逻辑表达上面的关系：当ΔI×V+ΔV×I=0 时，则正好是最大功率点；当ΔI×V+ΔV×I>0 且ΔV>0 或者ΔI×V+ΔV×I<0 且ΔV<0时，则此时输出功率处于最大功率点左侧；当ΔI×V+ΔV×I>0 且ΔV<0 或者ΔI×V+ΔV×I<0 且ΔV>0 时，则此时输出功率处于最大功率点右侧；此外，在实际采集中，ΔI×V+ΔV×I=0 的比较运算必将产生不必要的扰动，于是将|ΔI×V+ΔV×I|值控制在0.05误差范围内近似认为等于0，图5 为优化后电导增量算法的流程图。

图5 优化后电导增量算法的流程图

3 电导增量法仿真及结果分析

基于上述仿真平台对传统电导增量算法及优化后算法进行了仿真模拟。用2 和4 s 处出现突变的信号分别模拟光照强度由1 000 W/m2到500 W/m2和500 W/m2到700 W/m2的突变，模拟结果如图6～图7所示。

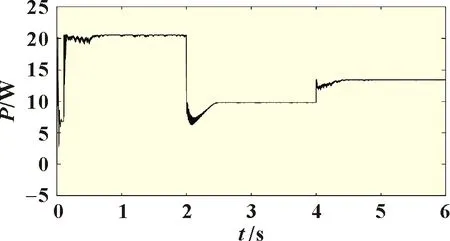
图6 传统电导增量算法模拟仿真结果

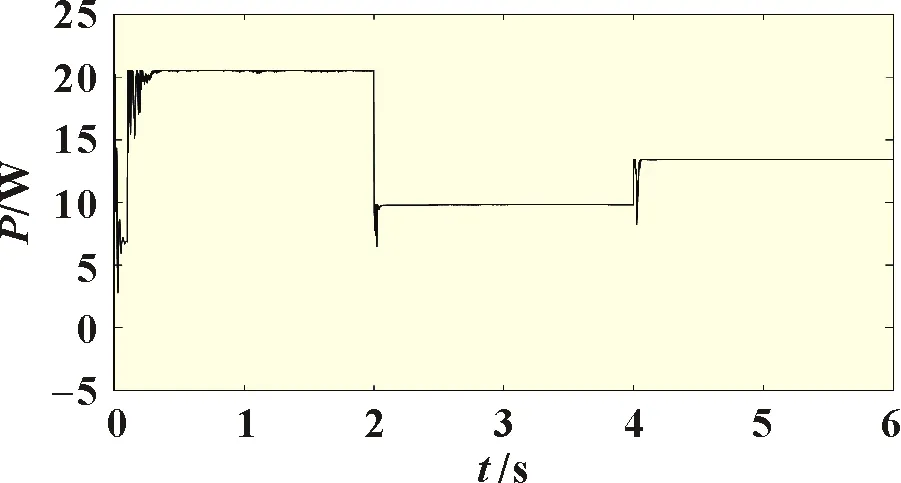
图7 优化后电导增量算法模拟仿真结果

图6 为传统电导增量算法模拟仿真结果，图7 为优化后电导增量算法模拟仿真结果。两者数据对比发现：在响应速度和稳定性能方面，优化后电导增量算法明显优于传统电导增量算法。在光照强度由1 000 W/m2到500 W/m2和500 W/m2到700 W/m2的跃变过程中，优化后电导增量法的响应速度分别提到了大约90%和80%。而在三种光照强度下，优化后电导增量法的稳态误差范围也提高了约50%左右。

4 结论

基于Proteus 仿真软件设计了Arduino 光伏系统MPPT 算法仿真平台，并将其应用于电导增量法的仿真模拟中，结果表明，该仿真平台不仅能可靠运行，而且只需改变仿真平台Arduino 微处理器的算法程序就可以对传统电导增量法响应慢、稳定性差的缺陷进行改进，从而给出了优化的电导增量法，最终实现了电导增量法的动态震荡和响应速度的良好平衡。