基于多核CPU的表约束并行传播模式研究∗
2021-11-09陈佳楠李占山1
陈佳楠,李 哲,李占山1,
1(吉林大学 软件学院,吉林 长春 130012)
2(吉林大学 计算机科学与技术学院,吉林 长春 130012)
3(符号计算与知识工程教育部重点实验室(吉林大学),吉林 长春 130012)
约束程序(constraint programming,简称CP)是一种求解组合优化问题的有效方法,在人工智能、运筹学、图论等诸多领域都有广泛的应用.并行计算是在不改变预期结果的情况下,同时对问题的多个部分进行处理的能力.随着计算机并行处理能力的发展,约束程序与并行计算的结合研究已成为被关注的领域,即并行约束程序.
针对并行约束程序的研究大致可分为以下几类:并行传播、搜索空间分割、组合算法和问题分解等[1].其中,并行传播是指并行执行在约束上的过滤算法,其研究意义在于利用并行计算提高约束传播的效率.但这种并行化操作并不简单,会出现变量论域的同步问题,具有一定的挑战性[2],因此只有少数有关并行传播的研究成果.比如:Rolf 等人[3]提出了维持约束网络并行相容性的两种传播模型,分别是使用共享中间论域的传播模型和使用局部中间论域的传播模型;李哲等人[4]给出了一种适合GPU 运算的并行弧相容算法AC4GPU.
由于缺少相应的表约束并行过滤算法,Rolf 等人提出的传播模型不能直接应用在对表约束的并行传播上.根据我们掌握的资料,目前还没有针对表约束并行传播的研究成果被公布.表约束是约束程序中最常用的约束类型之一,也被称为外延约束,每个约束在包含的变量集上显式地列举出所有支持或禁止的取值组合.表约束理论上可以编码任何类型的约束,在许多应用程序领域中,当对组合问题进行建模时,常常需要使用它们.
维持表约束网络广义弧相容(generalized arc consistency,简称GAC)的串行传播模式由串行传播算法和串行过滤算法两部分组成,串行传播算法串行执行维持表约束GAC 的串行过滤算法.过去的十多年中,维持表约束GAC 的串行过滤算法研究已经公布了大量的成果,其中具有代表性的系列成果是基于简单表缩减的串行过滤算法(若无特殊说明,后文的过滤算法均指基于简单表缩减的过滤算法).比如:STR(simple tabular reduction)[5]能够动态地维持表约束的有效元组;在STR 的基础上,STR2[6]在检查元组的有效性和收集被支持的取值时仅考虑相关的变量子集;STR3[7]通过使用dual table 等数据结构,避免了不必要的表遍历;STRbit[8]采用位向量编码dual table,大幅度地提升了过滤效率;CT(compact table)[9]使用以位向量为基础的sparse bit-sets,进一步加快了过滤速度;STR-N[10]能够直接作用于负表约束,其求解效率具有明显的优势;AdaptiveSTR[11]通过自适应地检测并删除无效元组,改进了STR3,使得算法速度显著提升;STR2*[12]采用了一种动态维持元组集有效部分的全新方法,拥有比STR2 和STR3 更高的效率.
根据维持表约束网络 GAC 的串行传播模式,我们提出了维持表约束网络临时广义弧相容(temporary generalized arc consistency,简称TGAC)的并行传播模式.该模式基于多核CPU,由并行传播算法和并行过滤算法两部分组成,并行传播算法利用线程池并行执行维持表约束TGAC 的并行过滤算法.之后,我们给出了并行传播模式的可靠性证明,即并行传播模式也维持表约束网络GAC.接下来,我们分析了并行传播模式的最坏时间复杂度,并将其与串行传播模式的最坏时间复杂度进行对比;经过分析对比,我们认为,并行传播模式在平均过滤时间较长的实例上要快于串行传播模式.最终的实验结果也验证了上述结论,而且并行传播模式在多数实例集上取得了从1.4~3.4 不等的加速比.
本文第1 节介绍相关的背景知识.第2 节回顾维持表约束网络GAC 的串行传播模式.第3 节给出维持表约束网络TGAC 的并行传播模式.第4 节展示实验结果.第5 节做出工作总结和未来展望.
1 背景知识
1.1 约束满足问题
一个约束网络N由一个变量集X和一个约束集C组成,其中:X包含n个变量,C包含e个约束.每个变量x有一个初始论域D(x),D(x)是x的初始取值集合;dom(x)表示在回溯搜索中变量x的当前论域(若无特殊说明,后文的论域均指当前论域),(x,a)表示变量x在dom(x)中的取值a.每个约束c都包含一个有序的变量集合scp(c),scp(c)被称为c的作用域,是变量集X的子集.相应地,每个变量x有一个约束订阅集sbp(x)={c|x∈scp(c)}.约束c的元数r为|scp(c)|,即c所包含的变量个数.约束c在语义上由一个关系rel(c)定义,rel(c)包含c所允许的元组集合.(正)表约束c通过列出所允许的元组来表示rel(c).约束网络N的解是对所有变量的一组赋值,这组赋值满足所有的约束.约束满足问题(constraint satisfaction problem,简称CSP)确定一个约束网络N是否有解.
例1:变量x和y的初始论域分别为D(x)={3,4,5}和D(y)={3,4},约束x>y可用表约束c表示,即scp(c)={x,y},rel(c)={(4,3),(5,3),(5,4)}.
τ=(a1,a2,...,ar)是约束c中的一个元组,其第i个值被表示为τ[xi].元组τ∈rel(c)是有效的当且仅当∀i∈{1,...,r},τ[xi]∈dom(xi);否则,τ是无效的.如果元组τ是有效的,则称τ是约束c的一个支持.进一步地,如果元组τ是约束c的一个支持且τ[x]=a,则称τ是c中对(x,a)的一个支持.
定义1(广义弧相容(GAC)).
•取值(x,a)是GAC 的当且仅当∀c∈sbp(x),c中至少存在一个对(x,a)的支持;
•约束c是GAC 的当且仅当∀x∈scp(c),.∀a∈dom(x),c中至少存在一个对(x,a)的支持;
•约束网络N是GAC 的当且仅当∀c∈C,c是GAC 的.
为了降低并行传播过程中不同线程同时访问同一变量论域的频率,Rolf 等人[3]提出了局部中间论域,对于变量x∈scp(c),局部中间论域domc(x)是dom(x)在约束c中的副本.我们称元组τ∈rel(c)是临时有效的当且仅当∀i∈{1,...,r},τ[xi]∈domc(xi);否则,τ是无效的.如果元组τ是临时有效的,则称τ是约束c的临时支持.进一步地,如果元组τ是约束c的临时支持且τ[x]=a,则称τ是c中对(x,a)的临时支持.
接下来,我们给出临时广义弧相容的定义和性质.
定义2(临时广义弧相容(TGAC)).
•取值(x,a)是TGAC 的当且仅当∀c∈sbp(x),c中至少存在一个对(x,a)的临时支持;
•约束c是TGAC 的当且仅当∀x∈scp(c),∀a∈domc(x),c中至少存在一个对(x,a)的临时支持;
•约束网络N是TGAC 的当且仅当∀c∈C,c是TGAC 的.
性质1.取值(x,a)是GAC 的,且∀c∈sbp(x),∀y∈scp(c),domc(y)=dom(y),那么(x,a)是TGAC 的.
证明:因为取值(x,a)是 GAC 的,所以∀c∈sbp(x),c中存在对(x,a)的支持τc.又因为∀c∈sbp(x),∀y∈scp(c),domc(y)=dom(y),所以∀c∈sbp(x),τc是c中对(x,a)的临时支持,故(x,a)是TGAC 的.证毕.□
性质2.约束c 是GAC 的,且∀x∈scp(c),domc(x)=dom(x),那么c是TGAC 的.
证明:因为约束c是GAC 的,所以∀x∈scp(c),∀a∈dom(x),c中存在对(x,a)的支持τc.又因为∀x∈scp(c),domc(x)=dom(x),所以∀x∈scp(c),∀a∈domc(x),τc是c中对(x,a)的临时支持,故c是TGAC 的.证毕.□
性质3.约束网络N是GAC 的,且∀c∈C,∀x∈scp(c),domc(x)=dom(x),那么N是TGAC 的.
证明:因为约束网络N是GAC 的,所以∀c∈C,c是GAC 的.又因为∀c∈C,∀x∈scp(c),domc(x)=dom(x),由性质2 可知∀c∈C,c是TGAC 的,故N是TGAC 的.证毕.□
1.2 线程池
线程池是一种多线程处理形式,管理一组线程,以便并行处理大量任务.在需要多次使用线程的并行程序中,单独创建与销毁线程会增加运行开销,从而影响程序的整体性能.而线程池通过限制线程的数量和重用线程,能够避免创建与销毁线程的代价,还可以提高程序的稳定性.
本文使用的是工作窃取线程池,其中每个线程都有一个独立的任务队列,主线程将任务分配到各个线程的任务队列中.工作窃取是指如果某个线程完成了其队列中的所有任务,而其他线程的队列中还有未处理任务,那么空闲线程可以窃取其他线程的未处理任务,从而改善了并行程序的负载均衡.
1.3 位向量
位向量是由若干个位(bit)组成的向量,具有存储空间占用少和处理速度快的特点.在构建一个CP 求解器时,位向量是变量论域的重要表示方式之一[13].另外,维持表约束GAC 的串行过滤算法STRbit[8]和CT[9]正是通过使用位向量才得以大幅度地加快过滤速度.
为了便于说明位向量的数据结构及其操作,我们用v表示位向量.位向量v由m个位组成,其第i个位由v[i]表示.特别地,0b 和1b 分别表示位的二进制取值.
本文共涉及以下6 种有关位向量的基本操作.
(1)位赋值操作:将位向量的某个位赋值为0b 或1b,如v[i]:=0b;
(2)位判等操作:判断位向量的某个位是否为0b 或1b,如v[i]=0b;
(3)位向量赋值操作:对位向量的整体进行赋值,如v:=0 是将位向量v的每个位均赋值为0b;又如,v:=v′是将位向量v′整体赋值给位向量v;
(4)位向量判等操作:判断位向量的整体取值,如v=0 是判断位向量v中每个位是否均为0b;
(5)位向量按位或操作:将两个位向量的对应位进行或运算,如v|v′;
(6)位向量按位与操作:将两个位向量的对应位进行与运算,如v&v′.
例2:位向量v和v′均由8 个位组成,它们的取值及经过v:=v&v′操作的结果如图1所示.

Fig.1 Bit vectors and their operations图1 位向量及其操作
在本文的相关算法中,我们用位向量bitdom(x)和bitdomc(x)分别表示变量x的论域dom(x)和x在约束c中的局部中间论域domc(x).设x的初始论域D(x)⊆[1,M],那么bitdom(x)和bitdomc(x)均由M个位组成.bitdom(x)[a]为1b 当且仅当a∈dom(x),bitdom(x)为0 当且仅当dom(x)为空.同理,bitdomc(x)[a]为1b 当且仅当a∈domc(x),bitdomc(x)为0 当且仅当domc(x)为空.
2 串行传播模式
维持表约束网络GAC 的串行传播模式由串行传播算法和串行过滤算法两部分组成,本节将依次介绍这两部分算法,并分析串行传播模式的相关性质.
2.1 串行传播算法
求解CSP 实例的常用方法是回溯搜索,回溯搜索是一种完整方法,它通过系统地探索实例的搜索空间,可找到全部的解或者证明无解存在.MAC(maintaining arc consistency)算法[14]是一种在搜索过程中维持约束网络GAC 的回溯搜索算法,目前被认为是求解CSP 实例最有效的完整方法.在MAC 算法中,当初始化约束网络、一个变量被赋值或者一个变量被删值时,串行传播算法会被调用执行,以维持约束网络GAC.
常用的串行传播算法之一是面向变量的串行传播算法[15,16],面向变量是指传播集合中保存引发传播的变量.针对不同类型的过滤算法,面向变量的串行传播算法会有所不同.我们使用的串行传播算法[17]具体见算法1和算法2.
算法1.serialPropagate(Xevt:set of variables):Boolean.


在算法1 中,Q是一个变量集合,保存引发传播的变量,即:当一个变量的论域被删值时,该变量会被添加至Q中.串行传播算法通过使用时间戳来避免不必要的工作,时间戳是一个值,表示某个事件发生的时间.变量x的时间戳stamp(x)表示最近一次从dom(x)中删除值的时间,约束c的时间戳stamp(c)表示最近一次在c上维持GAC的时间.时间通过计数器time来模拟.time,stamp(x)和stamp(c)均被初始化为0.
算法1 的传入参数Xevt是引发初始传播的变量集合,其中的变量会被添加至Q中.算法1 第6 行从Q中选出一个变量x后,对包含x的每个约束c,如果stamp(x)大于stamp(c),算法1 第8 行会执行在c上维持GAC 的串行过滤算法.串行过滤算法会返回由被删值的变量组成的集合,并且如果有一个变量的论域被删空,串行过滤算法会将不相容标识inconsistent置为true,之后,inconsistent会在算法1 第9 行被识别出,这表明传播失败,当前表约束网络无解,MAC 算法发生回溯.当Q中的所有变量均被选出传播后,并且传播期间没有变量的论域被删空,这表明传播成功,当前表约束网络是GAC 的,MAC 算法继续搜索.
2.2 串行过滤算法
如前文所述,维持表约束GAC 的串行过滤算法研究已经公布了大量成果,它们的设计实现虽然有所不同,但主要由更新表(算法4)和过滤论域(算法5)两部分组成.我们总结了它们的共同之处,具体见算法3~算法5.
算法3.enforceGAC(c):set of variables.

算法5.filterDomains(c):set of variables.

算法3 中,串行过滤算法首先更新表,即移除无效的元组(算法4 第4 行);进而过滤论域,即删除在该约束上不存在支持的值(算法5 第5 行);最后返回由被删值的变量所组成的集合.如果有一个变量x的论域被删空,即bitdom(x)的每个位均变为0b,不相容标识inconsistent将被置为true(算法5 第8 行).
2.3 性质分析
因为不同的串行过滤算法有不同的最坏时间复杂度,所以它们的最坏时间复杂度被统一设为O(T).另外,我们用rmax和dmax分别表示最大的约束元数和最大的初始论域大小,即rmax=maxc∈C|scp(c)|,dmax=maxx∈X|D(x)|.
性质4.维持表约束网络GAC 的串行传播模式的最坏时间复杂度为O(ermaxdmaxT)[17].
证明:串行传播算法中,初始化变量集合Q的时间代价为O(n)(算法1 第2 行、第3 行).对于x∈scp(c),每当一个值(x,a)被删除后,约束c会被执行一次维持GAC 的串行过滤算法,那么约束集C中的所有约束被执行串行过滤算法的总次数最多为ermaxdmax(算法1 第7 行).而执行一次串行过滤算法的时间代价为O(T)(算法1 第8 行),将串行过滤算法返回的变量集并入Q的时间代价为O(rmax)(算法1 第11 行、第12 行),并且其他所有语句的时间代价均为O(1),所以串行传播模式的总体时间代价为O(n+ermaxdmax(T+rmax)).又因为n=O(ermax),且T>>rmax,故维持表约束网络GAC 的串行传播模式的最坏时间复杂度为O(ermaxdmaxT).证毕.□
3 并行传播模式
在本节中,我们提出了维持表约束网络TGAC 的并行传播模式,它同样由并行传播算法和并行过滤算法两部分组成.之后,我们分析了并行传播模式的相关性质.
3.1 并行传播算法
在并行传播模式中,我们引入了一些新的数据结构.
•约束位标识tableMask:由e个位组成的位向量,用以标记需要执行并行过滤算法的表约束,在并行传播模式中是被动态更新的.其第i个位用tableMask[ci]表示,tableMask[ci]为1b 当且仅当约束ci需要被执行并行过滤算法;
•位订阅bitSbp(x):由e个位组成的位向量,与变量x的约束订阅集sbp(x)相对应,第i个位用bitSbp(x)[ci]表示,bitSbp(x)[ci]为1b 当且仅当x∈scp(ci).
通过tableMask:=tableMask|bitSbp(x)可将bitSbp(x)提交至tableMask上.
例3:约束网络N的约束集C={c1,c2,...,c8},变量x和y的约束订阅集分别为sbp(x)={c4,c8}和sbp(y)={c1,c8},相应的位订阅bitSbp(x)和bitSbp(y)如图2所示.约束位标识tableMask初始化为0(全部位均为0b),将bitSbp(x)提交至tableMask的操作及结果如图2所示.

Fig.2 Bit subscriptions and their submission operations图2 位订阅及其提交操作
如前文所述,串行传播算法根据变量传播集合顺次执行对相关约束的过滤任务(算法1 第7 行、第8 行),我们将这一操作并行化,提出了并行传播算法.并行传播算法使用约束位标识tableMask标记相关的表约束,对这些表约束的过滤任务被动态提交至线程池中并行执行,直到发生了论域删空事件或者没有新的过滤任务.具体见算法6.
算法6.parallelPropagate(Xevt:set of variables):Boolean.

算法6 的传入参数Xevt同样是引发初始传播的变量集合,其中的变量被用于初始化约束位标识tableMask(第2 行、第3 行).submitMask是一个保存tableMask的局部临时标识(第6 行),因为tableMask会被动态更新,所以算法6 根据submitMask向线程池pool提交在约束c上维持TGAC 的并行过滤任务(第9 行、第10 行),之后需要等待它们完成(第11 行).在并行过滤任务的执行期间,当一个变量的论域被删值后,论域改变标识varChanged被置为true,并且tableMask被更新,以在算法6 的下次循环中向线程池pool提交新的并行过滤任务;如果有一个变量的论域被删空,不相容标识inconsistent被置为true,之后会被识别出(第12 行),这表明传播失败(第13 行),当前表约束网络无解,MAC 算法发生回溯.如果所有的并行过滤任务被执行完成后,varChanged仍为flase,即没有发生删值事件,那么循环结束,这表明传播成功(第15 行),当前表约束网络是TGAC 的,MAC 算法继续搜索.
3.2 并行过滤算法
我们对维持表约束GAC 的串行过滤算法进行扩展,得到了维持表约束TGAC 的并行过滤算法(算法7),如PSTR2,PSTR3,PSTRbit 和PCT,并进行了一般化总结,它们同样主要由更新表(算法8)和过滤论域(算法9)两部分组成.
算法7.enforceTGAC(c).

算法8.updateTTable(c).

Table 2 Average results to solve instances from different series(STRbit and PSTRbit)表2 不同实例集的平均实验结果(STRbit 和PSTRbit)

算法9.filterTDomains(c).

与算法3 不同的是,算法7 首先判断不相容标识inconsistent是否为真:如果为真,算法7 返回,即所有的线程能够及时终止并行过滤任务;如果为假,算法7 将每个变量x∈scp(c)在c中的局部中间论域bitdomc(x)更新至最新的bitdom(x);然后,算法7 更新表,即移除无效的元组(算法8 第4 行);最后,算法7 过滤论域,即先从局部中间论域bitdomc(x)中删除在该约束上不存在临时支持的值(算法9 第4 行).若局部中间论域bitdomc(x)被删值,算法9便将bitdom(x)与bitdomc(x)的按位与结果赋值给bitdom(x),即从bitdom(x)中删除不存在于bitdomc(x)中的值(算法9 第6 行).进一步地,如果bitdom(x)被删空,即bitdom(x)的每个位均为0b,全局不相容标识inconsistent被置为true(算法9 第8 行),并行过滤算法结束;否则,论域改变标识varChanged被置为true(算法9 第10 行),并且变量x的位订阅bitSbp(x)被提交至约束位标识tableMask上(算法9 第11 行),即与x有关的约束c需要参与下一次并行传播.
多个线程在并行执行对不同表约束的并行过滤算法时,可能会同时过滤同一个变量x的论域bitdom(x)(算法9 第6 行),也可能会同时更新约束位标识tableMask(算法9 第11 行),所以我们对这两种操作采用了非阻塞同步方式,通过比较并替换(compare and swap,简称CAS)实现,以确保并行过滤算法的正确性.
例4:表约束c1,c2∈sbp(x)被两个线程并行执行维持TGAC 的并行过滤算法,两个线程同时过滤变量x的论域bitdom(x),过程及结果如图3所示.
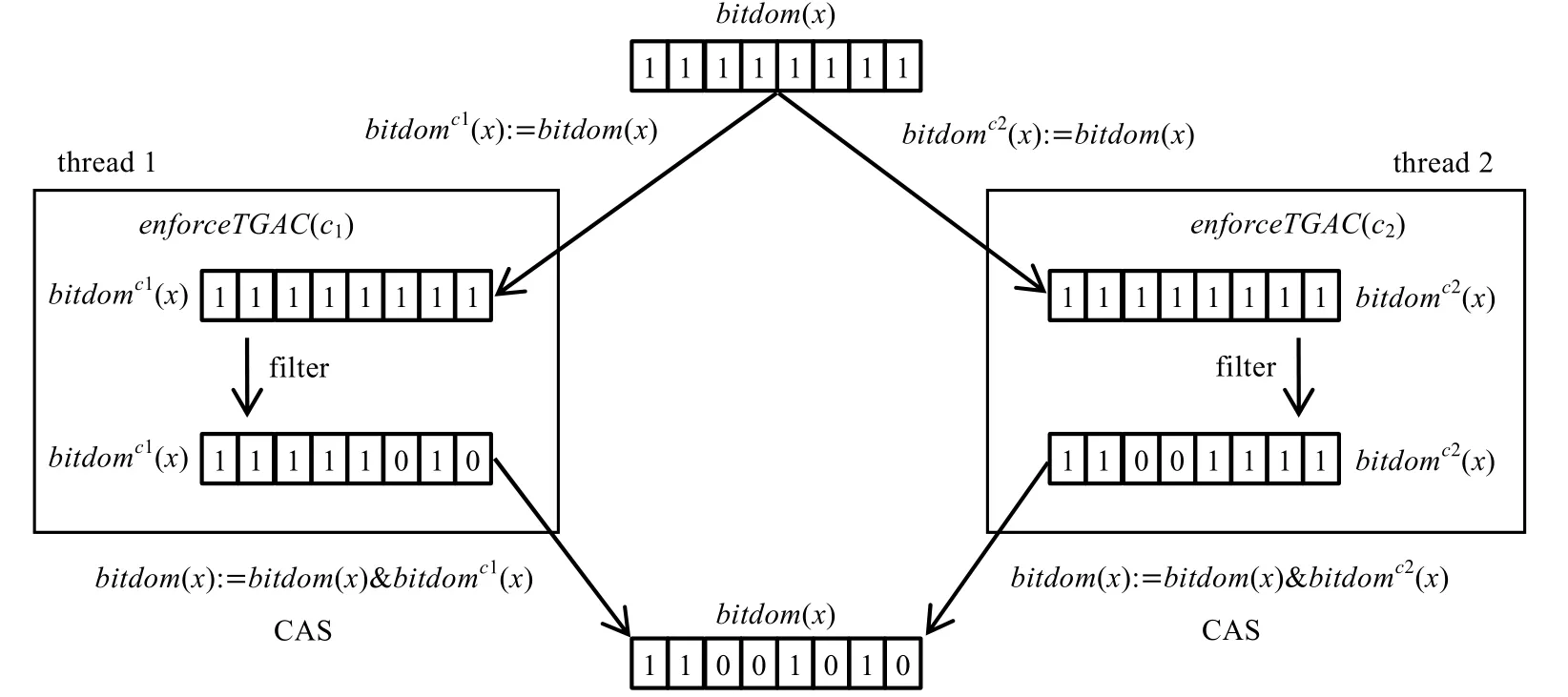
Fig.3 Parallel filtering algorithm execution instance图3 并行过滤算法执行实例
3.3 性质分析
首先,我们给出并行传播模式的可靠性证明.
性质5.维持表约束网络TGAC 的并行传播模式也维持表约束网络GAC.
证明:一方面,如果取值(x,a)不是GAC 的,即∃c0∈sbp(x),c0中没有对(x,a)的支持,那么当c0被执行维持TGAC的并行过滤算法时,scp(c0)内各变量的局部中间论域均被更新(算法7 第3 行、第4 行),因此c0中也没有对(x,a)的临时支持,(x,a)不是TGAC 的,会被删除(算法9 第4 行、第6 行).
另一方面,如果取值(x,a)是GAC 的,那么∀c∈sbp(x),当scp(c)内各变量的局部中间论域均被更新后(算法7第3 行、第4 行),有∀y∈scp(c),domc(y)=dom(y).由性质1 可知,(x,a)是TGAC 的,会被保留.
综上所述,维持表约束网络TGAC 的并行传播模式也维持表约束网络GAC.证毕.□
接下来,我们对并行传播模式的最坏时间复杂度进行分析.通过对比串行过滤算法,因为并行过滤算法中所增加的操作语句均有着O(rmax)(算法7 第3 行、第4 行)或O(1)的时间代价,并且T>>rmax,所以并行过滤算法的最坏时间复杂度也为O(T).线程池的并行度用p表示,即线程池内存在p个线程.另外,每个并行过滤任务被提交至线程池之后,在线程池中还会有被调度的时间代价,我们将其设为O(Sp),Sp随着并行度p的增大而增大.
性质6.维持表约束网络TGAC 的并行传播模式的最坏时间复杂度为O(ermaxdmax(Sp+T)/p).
证明:并行传播算法中初始化约束位标识tableMask的时间代价为O(n)(算法6第2 行、第3行)且n=O(ermax).对于x∈scp(c),每当一个值(x,a)被删除后,约束c会被执行一次维持TGAC 的并行过滤算法,那么约束集C中的所有约束被执行并行过滤算法的总次数最多为ermaxdmax(算法6 第9 行).而每个并行过滤任务在线程池中被调度的时间代价为O(Sp),执行一次并行过滤算法的时间代价为O(T)(算法6 第10 行),并且其他所有语句的时间代价均为O(1),所以并行过滤任务的总体时间代价为O(ermaxdmax(Sp+T)).又因为并行过滤任务可被p个线程并行执行,所以维持表约束网络TGAC 的并行传播模式的最坏时间复杂度为O(ermaxdmax(Sp+T)/p).证毕.□
当并行度p>1 时,通过对比串行传播模式的最坏时间复杂度O(ermaxdmaxT)和并行传播模式的最坏时间复杂度O(ermaxdmax(Sp+T)/p),我们认为:若T>>Sp,那么O(ermaxdmax(Sp+T)/p)≈O(ermaxdmaxT/p),即并行传播模式在平均过滤时间较长的实例上相对串行传播模式能够取得较为明显的加速;若T< 我们在22 组CSP 实例集上使用MAC 算法分别测试了串行传播模式和并行传播模式.在串行传播模式下,串行过滤算法分别使用CT 和STRbit;在并行传播模式下,并行过滤算法分别使用PCT 和PSTRbit,线程池的并行度p依次被置为2,4 和6.MAC 算法采用dom/ddeg变量启发式和min 值启发式,dom/ddeg是稳定的变量启发式,能让两种传播模式在求解同一实例时拥有相同的变量选取顺序,进而实现公平的效率对比.每个实例的搜索时间上限为900 秒.实验环境为Intel Core i7 3.40GHz(4 cores)8GB RAM Windows10 64bit OS,程序编写语言是Java11.0.3 和Scala2.12.8.所有的实例集均来自http://www.cril.univ-artois.fr/~lecoutre/benchmarks.html,我们的测试代码可在https://github.com/amtfjlsj/lotus 上获取. 表1 和表2 给出了不同实例集的平均实验结果,实例集中,未超时的实例个数用#表示.time 表示求解实例所需的平均传播时间(单位s),每个实例集对应的最短平均传播时间被加粗;filt 表示在求解实例的过程中过滤算法被调用的平均次数(单位10 万);avg 表示执行一次串行过滤算法的平均时间(单位μs),即实例集的平均过滤时间,我们使用串行传播模式下time 与filt 的比值作为avg 的近似值;speed 是并行传播模式相对于串行传播模式的平均传播时间加速比,即串行平均传播时间与并行平均传播时间的比值. 首先,我们比较一下串行传播模式和并行传播模式的实验结果.在17 组实例集上,并行传播模式要快于串行传播模式,而且在多数实例集上取得了从1.4~3.4 不等的加速比;在另外5 组实例集上,并行传播模式的表现不如串行传播模式.从各实例集在串行传播模式下的平均过滤时间avg 可以看出:取得较好加速比的实例集,其avg 普遍较大,如rand-10-60,ogd,uk 和MDD0.9 等;并行传播效果不好的实例集,其avg 普遍较小,如aim-50,aim-100 和dubois 等.这与第3.3 节性质6 的分析相一致.因此,我们提出的并行传播模式适用于平均过滤时间avg较大的实例. 并行传播模式在多数实例集上取得了较好的加速比,但是没有实现线性加速(加速比与并行度相等),原因主要有两点. •在求解实例的过程中,并行过滤算法被调用的平均次数filt 多于串行过滤算法被调用的平均次数filt. 虽然并行传播模式有多个线程并行执行过滤算法,但其工作总量并不与串行传播模式的工作总量相等,而是随着线程的增多而增加.这是因为在并行传播模式下,线程之间不能相互通信.对表约束c执行并行过滤算法的线程只在初始时更新变量x∈scp(c)在c中的局部中间论域bitdomc(x),到算法结束前不再获取最新的bitdom(x).那么在此过程中,如果其他线程删除了bitdom(x)中的值,c需要被重新执行一次并行过滤算法以获取最新的bitdom(x).这种现象在过滤算法被顺次执行的串行传播模式中是不存在的. 例5:现有两个表约束c1和c2,其中,scp(c1)={x,y},scp(c2)={x,z,u}.假设取值(y,a)和(z,a)被其他表约束删除,这导致c1和c2被执行过滤算法.在串行传播模式下,首先线程t对c1执行串行过滤算法,t从bitdom(x)中删除了(x,a);之后,在t对c2执行串行过滤算法时,(x,a)的移除导致t从bitdom(u)中删除了(u,a).在并行传播模式下,c1和c2同时被两个线程t1和t2分别执行并行过滤算法:首先,bitdomc1(x)和bitdomc2(x)被更新至最新的bitdom(x);之后,t1从bitdom(x)中删除了(x,a),但(x,a)仍存在于bitdomc2(x)中,因此t2没有从bitdom(u)中删除(u,a);因为(x,a)的删除,c1和c2需要再次被t1和t2分别执行并行过滤算法,其中,t2将bitdomc2(x)更新至最新的bitdom(x),进而从bitdom(u)中删除了(u,a).过程如图4所示,同样的情况下,串行过滤算法被执行了2 次,而并行过滤算法被执行了4 次. Fig.4 An example of serial propagation mode versus parallel propagation mode图4 串行传播模式与并行传播模式的对比实例 •并行传播进程中线程利用率并不总是100%. 线程利用率是活跃线程数与并行度的比率,活跃线程是指正在运行任务的线程.我们在求解一个实例的并行传播(并行度p为4)进程中获取了活跃线程的数目,其随时间点的关系如图5所示:一方面,并行传播模式也存在串行分量,比如算法6 除第9 行~第11 行之外的部分,在执行这部分串行分量时,活跃线程只有1 个,线程利用率为25%;另一方面,当线程池中的并行过滤任务数小于并行度时,活跃线程数将等于任务数,线程利用率小于100%. Fig.5 Number of active threads in a parallel propagation process图5 并行传播进程中的活跃线程数 最后,我们对比一下并行传播模式在不同并行度p下的平均传播时间.p为4 的并行传播模式在大多数实例集上均快于p为2 的并行传播模式,但p为6 的并行传播模式在多数实例集上却不如p为4 的并行传播模式.我们认为:实验环境的CPU 为4 核处理器,因此当并行度高于核数时,并行传播进程中会出现多个线程抢占同一个核的情况,从而导致平均传播时间变长. 在本文中,首先,我们提出了维持表约束网络TGAC 的并行传播模式,该模式基于多核CPU,由并行传播算法和并行过滤算法两部分组成,并行传播算法利用线程池并行执行维持表约束TGAC 的并行过滤算法;之后,我们给出了并行传播模式的可靠性证明,即并行传播模式也维持表约束网络GAC;另外,通过对并行传播模式的最坏时间复杂度分析,我们认为并行传播模式在平均过滤时间较长的实例上要快于串行传播模式,最终的实验结果也验证了这一结论. 基于本文的思路,我们认为未来的研究可从以下3 个方面继续开展. 1)我们在实验分析中给出了两点关于并行传播模式没有实现线性加速的原因,因此未来的研究可尝试通过减少并行传播模式的工作总量或提高线程利用率,来进一步提升并行传播的效率; 2)维持表约束GAC 的串行过滤算法研究除了基于简单表缩减,还有很多基于其他设计思想的成果,比如泛型过滤算法系列(GAC2001[18],GAC3rm[19],GAC4R[20]等)和压缩表示过滤算法系列(MDDc[21],MDD4R[20],AdaptiveMDDc[11]等),这些串行过滤算法均可转化成维持表约束TGAC 的并行过滤算法; 3)在相容性理论方面,删值能力强于GAC 的相容性被称为高阶相容性,如最大限制成对相容性(max restricted pairwise consistency,简称maxRPWC)和成对相容性(pairwise consistency,简称PWC).维持表约束网络高阶相容性的串行传播模式设计受到了很多研究工作的关注[22−24],因此未来的研究可尝试设计实现维持表约束网络高阶相容性的并行传播模式.4 实验结果


5 总结
