快速DOA估计算法研究

王传宇，聂慧锋，王 林，胡异炜，赵荣崎

(中国船舶重工集团公司第七二三研究所，江苏 扬州 225101)

0 引 言

多信号分类(MUISC)算法[1]的主要原理就是通过信号子空间与噪声子空间的正交性实现到达方向(DOA)估计，但是传统的MUISC算法需要通过特征分解获得信号子空间和噪声子空间、再通过谱峰搜索估计出信号的入射角度。其中的特征分解较为复杂，谱峰搜索运算量较大，因此不利于现场可编程门阵列(FPGA)的工程实现。众多学者针对子空间类算法的快速DOA估计进行了研究，Zoltowski等人通过维纳滤波器的递推算法,找到一个与信号子空间正交的投影矩阵，从而进行DOA估计。文献[2]～[3]中Goldstein等人提出了多级维纳滤波(MSWF)，该算法不需要进行特征分解，具有很强的降维能力且收敛速度更快。文献[4]中艾名舜、马红光等人利用均匀线阵导向矢量的Vandermonde结构，推导出了噪声子空间的解析形式，该算法不需要计算接收数据的协方差矩阵，也不需要进行矩阵分解。文献[5]中于智龙、沈峰利用传播算子和空间平滑相结合的方式实现了快速解相干的DOA估计。文献[6]中闫锋刚提出了压缩谱理论，能够有效降低谱峰搜索的运算量。本文对传播算子和压缩谱算法进行了研究，通过传播算子和压缩谱相结合的方式进行快速DOA估计，经过仿真验证，具有良好的估计性能且能够有效降低子空间算法的高复杂度和高运算量的问题。

1 MUSIC算法原理

如图1所示，M个窄带远场信号入射到由N个天线组成的阵列。

图1 阵列入射模型

其阵列接收模型为：

X(t)=A(θ)S(t)+N(t)

(1)

求解阵列数据的协方差矩阵:

R=E[XXH]=

AE[SSH]AH+σ2I=

ARsAH+RN

(2)

由于信号与噪声相互独立，对协方差矩阵R进行特征分解，可以得到下式:

R=UsΛsUs+UNΛNUN

(3)

式中:Us为信号子空间；UN为噪声子空间。

由于信号子空间与噪声子空间的正交性且可以使用式(4)进行谱估计，谱函数中的最小值位置即为信号的真实入射角度:

(4)

2 传播算子(PM)算法

在实际工程应用中，MUSIC算法由于特征分解的复杂度和运算量较高，不利于工程实现，使用传播算子(PM)算法可以通过一种线性运算快速得到子空间，在求得噪声子空间及其投影算子时无需进行特征分解。现将式(1)中的阵列流型阵A(θ)进行分块：

(5)

式中:A1(θ)为M×M维的矩阵；A2(θ)为(N-M)×M维的矩阵。

若A1(θ)为非奇异矩阵，那么A1(θ)和A2(θ)之间存在一个唯一的矩阵P，满足线性关系：

A2(θ)=PHA1(θ)

(6)

矩阵P被称为传播算子。

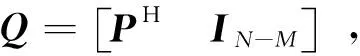
QHA=0

(7)

式(7)表明矩阵Q与噪声子空间具有正交性，即span{Q}=span{UN}，可以通过协方差矩阵直接求解矩阵P。

首先对协方差矩阵R进行分块：

(8)

(9)

根据得到的传播算子P即可构造矩阵Q，通过公式(10)进行谱峰搜索即可得到信号的入射角度:

θMUSIC=argmin{aH(θ)QQHa(θ)}

(10)

3 基于PM算法的压缩谱估计

导向矢量a(ω)可以写为如下形式：

(11)

式中：f为信号频率；d为阵元间距；c为光速。

对式(11)两边同时取共轭：

(12)

由于正弦函数是奇函数，故有：

(13)

因此可以得到：

aH(θ)Q=aT(-θ)Q=aH(-θ)Q*

(14)

根据公式(14)可以看出噪声子空间的共轭与信号的对称角度成正交性，即aH(-θ)Q*=O。可以根据PM算法重新构造公式(4)中的谱估计函数：

θMUSIC=argmin{aH(θ)QQHQ*QTa(θ)}

(15)

谱函数估计会在θ和-θ的位置同时出现极小值，在将θ和-θ代入公式(10)即可求出正确的入射角度，通过压缩谱的算法可以将谱峰搜索的范围减半，有效地减少了算法运算量。

算法步骤：

(1) 通过公式(8)对协方差矩阵R进行分块处理，得到子矩阵R1和R2。

(2) 通过公式(10)使用矩阵R1和R2求出传播算子P。

(3) 使用传播矩阵P构造与信号子空间正交的矩阵Q。

(4) 通过公式(15)构造压缩谱函数,进行谱峰搜索，求出峰值。

(5) 对峰值进行解模糊即可求出正确的信号入射角度。

4 算法仿真

阵列设为阵元数为12个的均匀线阵，阵元间距为半波长，阵元摆放如图1所示。入射信号为远场窄带信号，并且信号之间相互独立，噪声为相互独立的零均值加性高斯白噪声，信号与噪声之间相互独立。

4.1 信噪比对算法精度的影响

为了测量信噪比对算法的影响，设入射信号数目为1，信号的入射角度为阵列法线的近轴方向，在[-5°～+5°]内随机入射。噪声为加性高斯白噪声，信噪比范围为-10～20 dB，每间隔2 dB进行递增，信号的快拍数为100，每个信噪比下进行1 000次蒙特卡洛实验，统计实验结果求其均方根误差。

图2为信号的DOA测量误差，根据仿真结果可以看出2种算法的DOA估计精度随着信噪比增大而提高。当信噪比低于0 dB时，MUSIC算法的测角精度优于PM算法与压缩谱相结合的测向方式；当信噪比高于0 dB时，2种算法的估计性能相近，DOA估计具有较高的精度。

图2 DOA估计精度

4.2 算法分辨率仿真分析

为了测量算法的分辨力，入射信号的数目设为2个，通过改变2个信号与阵列法线方向的夹角，使2个信号之间的入射角度不同。信噪比为20 dB，快拍数为100，进行1 000次蒙特卡洛实验，统计其测角精度和正确分辨信号的成功率。

图3 为双信号随着入射角度不同其入射角的估计精度。图4为双信号随着入射角度不同其成功分辨的概率。根据图3可以看出，在双信号入射情况下，MUSIC算法的测角精度略优于PM算法与压缩谱相结合的测向方式。根据图4可以看出MUSIC算法的分辨力为2°，PM算法与压缩谱结合的测向分辨力为3°。因此，MUSIC算法的分辨力略优于PM算法与压缩谱，2种算法的分辨力性能接近。

图3 双信号测角精度

图4 双信号分辨成功概率

5 结束语

在信噪比较高的情况下，PM算法与压缩谱相结合的测向方式拥有与传统MUSIC算法相近的估计性能，具有较高的估计精度和较好的分辨力。同时PM算法与压缩谱相结合的测向方式的算法不需要进行特征分解，有效降低了算法的复杂度；将谱函数的搜索范围压缩了一半，有效降低了算法的运算量。该算法具有低复杂度、低运算量的优点，在工程应用中能够更好地节省硬件成本，具有一定的工程应用价值。