基于设备运行数据的风机故障诊断方法

邓媛媛,刘国奇,蔡 磊

(沈阳建筑大学理学院,辽宁 沈阳 110168)

随着可再生能源行业的发展,风能作为一种环保、可再生、无污染、可循环利用的新型能源,其发展受到世界各国风能行业的重视。根据统计,在2019年全球风电第一大市场,中国风电装机容量在全球遥遥领先,其发展态势迅猛。风力发电机(简称风机)作为将风能转化为电能的设备,长期处在极端温度、风沙等恶劣环境下,并承受了巨大的机械应力,极易发生各类机械、电器故障[1]。因此,风机故障诊断的研究变得越来越迫切。随着计算机的普及,通过在风机的关键部件上安装传感器,这些部件在运行时的状态会实时采集到计算机上,这些参数以秒为间隔进行采集,因此能够较确切地反映出部件的实时变化[2]。随着科学技术的发展,工业数据库中积累了大量历史数据,这其中包含海量关于风机故障时各采集点的测量参数,如何对这些数据记录分析、寻找规律,并用于风机故障诊断的研究有着重要的意义。

国内外许多学者已经提出了多种风机故障诊断方法,如E.Wolfgang[3]采用专家系统对汽车进行故障诊断;A.Widodo[4]提出了基于部件分析和支持向量机的发动机故障诊断方法。这些方法各有特点，虽然在实际中得到了一定的应用,但是对于处理不断产生的海量数据,以及不确定故障信息的容错性,仍然不太理想。针对以上问题,近些年产生了更多有效的方法,如针对数据挖掘技术的基于时间序列数据挖掘[5]、粗糙集理论算法[6]、贝叶斯网络算法[7]、决策树技术[8]等纷纷被引入到故障诊断中。而在探索过程中,关联规则挖掘作为一种重要的方法应用于数据挖掘技术中,这种方法不但能够发现隐藏在海量数据中有关联性且有价值的数据,也对决策树生成具有重要的使用价值,因此多被用在商业智能解决方案体系中,但在风机故障诊断研究中不常见。文献[9]提供了关联规则挖掘在商业智能中的重要应用。而文献[10]中虽然将关联规则挖掘应用到了变压器故障诊断中,但风力发电机与之有许多不同之处。

基于上述分析,笔者采用关联规则经典算法,将基于粗糙集理论的关联规则挖掘算法应用到风机故障诊断中,将风机各个监测点的参数作为条件属性,风机故障数据类型作为决策属性。首先利用粗糙集理论对条件属性进行约简,提取最佳属性进行约简组合处理,然后利用上面结果形成的约简决策表和关联规则挖掘诊断进行推理,最终得到诊断决策表。研究表明,诊断决策表有效地反映了条件属性和决策属性之间的关联关系,表明笔者提出的方法对风机故障诊断具有有效性,可为风机设备故障诊断和故障预测提供帮助。

1 数据来源

笔者使用的数据来自于内蒙古察右后旗红牧风电场,位于内蒙古中部阴山北麓,乌兰察布市后山地区,共安装24台单机容量为2 000 kW的风力发电机组,总装机容量为4.8万kW。笔者从红牧风场工业数据库采集样本数据,该数据库中存放了大量的风机状态信息,数据库中每一行数据记录为风机在一个特定时间点的状态,风机的状态是各部分传感器搜集到的参数决定的。数据集中原始数据包含139个参数,而这些数据参数采样的时间间隔平均为2s,这些数据包括平均有功功率、温度、压力、平均无功功率等106个定量化指标参数;对于以上定量化数据,笔者将其分为两种类型,一种是不断波动的参数取值,它们是不断变化的,比如电压、电流等;另外一种是在正常状态下恒定的参数取值,属于定性指标,例如液压制动压力、故障及状态报警等,这些数值是不能用来进行计算分析的。还有一些指标在行业内被叫做定性指标,这些定性指标使用报警码或故障码来代替特定的报警或者是故障,也被称为报警码或故障码,这些指标也不会在预测中被使用。风机参数分类的相关信息如表1所示。

表1 风机参数分类Table 1 Classification of wind turbine parameters

定性化的报警码或故障码在预测中也具有非常重要的作用,在收到任何一个报警码或者故障码后,都代表风机设备发生了故障。在实际的数据中,不同故障发生的频率差别很大,有一些故障一年发生很多次,而有一些故障多年也不发生一次;另外,故障也被划分为不同级别,级别越高则故障越严重。笔者选取发生次数多且报警级别高(4级)的故障的历史记录来进行研究。

在观察中发现,故障发生的次数和故障条目多少没有必然联系,因为有的故障发生一次可能持续一个小时甚至更长时间,而有的故障发生一次可能持续几秒钟。表2列举了21种常见的风机故障代码。

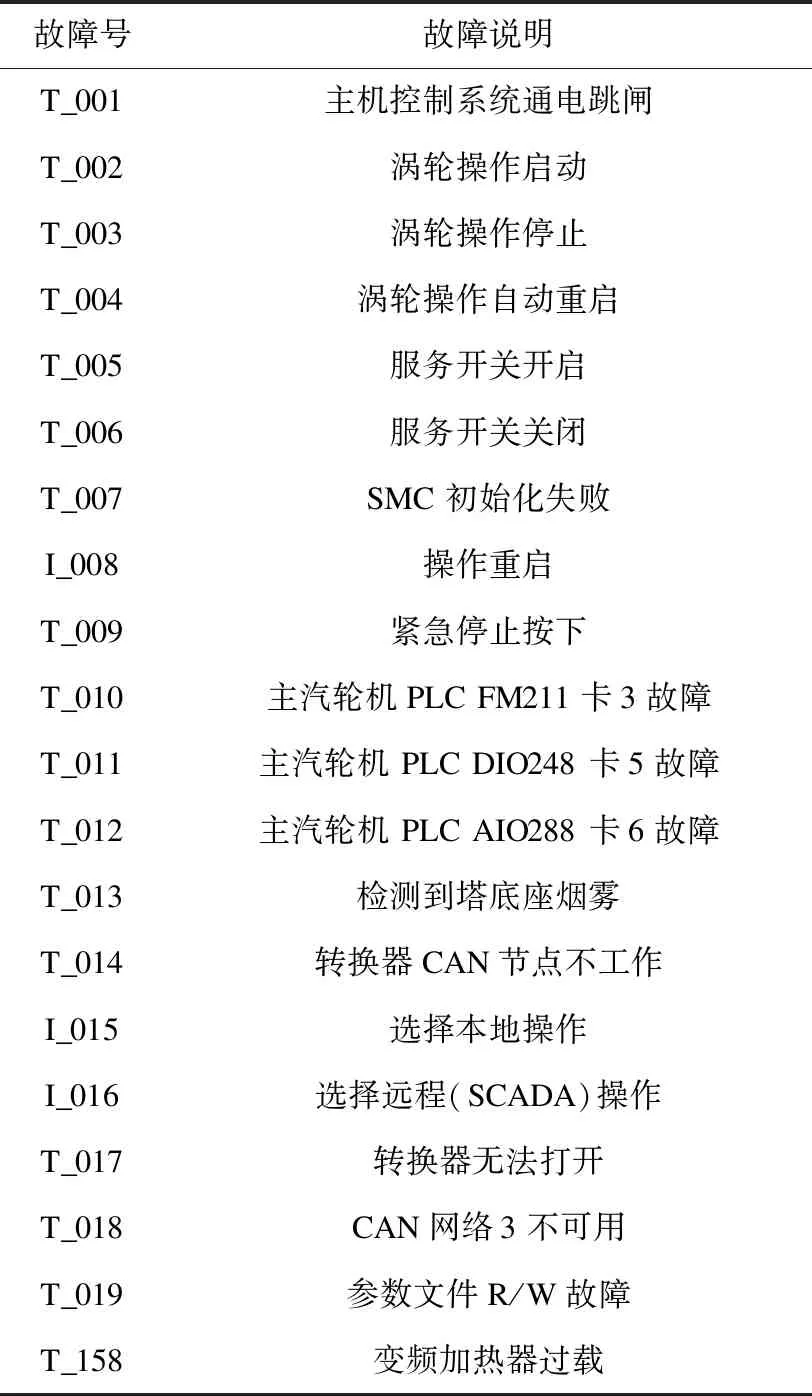
表2 风机故障实例及说明Table 2 Example and illustration of wind turbine faults

2 基于粗糙集理论和关联规则的风机故障诊断模型

2.1 基于Apriori算法的关联规则挖掘

故障诊断实际上是一种比较分类,在进行故障定位时,是将故障规则库与待诊断的故障参数值进行比较,把一个实时采集的故障信号归入到故障规则库中[11-13]。

图1为风机故障诊断模型图。该模型首先获取风机状态历史数据,使用粗糙集理论对风机的特征属性进行约简,得到最佳的风机状态属性子集,然后使用关联规则Apriori挖掘出数据中潜在的规则,专家对这些规则进行评估,将有意义的规则存入到数据库中,形成故障规则库。当需要对风机进行故障诊断时,只需将风机的实时参数与规则库中的规则进行匹配即可确定故障类型。

图1 风机故障诊断模型Fig.1 The model of fault diagnosis in wind turbine

定义1条件属性

A=(a1,a2,…,ak,…,ai)为条件属性集,其中ai为条件属性,即风机状态的表征参数或者风机状态属性。

定义偏移向量为风机故障条目参数取值形成的向量与正常条目参数取值的向量的差值。那么偏移向量分量为0，表示该分量对应的参数取值正常。

定义2决策属性

D={d1,d2,…,di}为决策属性集,di为决策属性,即风机故障类型。

定义3风机状态历史数据集

设U={u1,u2,…,ui,…,un}为风机状态历史数据集,其中ui为风机状态历史数据集,其中第i个样本,每个样本包含m个条件属性和1个决策树形,记作{A,D}。

定义4关联规则

形如r:X⟹Y的蕴含式,其中X⊆A,即条件属性的子集,Y∈D,即一种故障类型,R={r1,r2,…,ri,…,rk}为规则集。

算法基本思想:风机状态历史数据集U={u1,u2,…,ui,…,un},其中ui为第i个样本,每个样本包含m个条件属性和1个决策树形,记作{A,D}。首先对U进行二值化处理,所有数据都只有0和1两种取值,得到处理后的数据集S={s1,s2,…,si},然后利用粗糙集理论的基于区分矩阵和逻辑运算的条件属性约简算法对数据集S中的条件属性集合A={a1,a2,…,am}进行约简,得到条件属性集合A的子集AR={ak1,ak2,…,akp}(p⊂m),然后将数据集S中属性{AR,D}对应的列出去,得到新的数据集SN=(sn1,sn2,…,sni,…,snn),其中sni的属性为{AR,D}。接着使用关联规则挖掘出决策表中满足最小置信度和最小支持度的规则集R={r1,r2,…,rn}。

2.2 相关定义

给出定义相关的概念如下：

定义5首先给定一组故障参数信息R={r1,r2,…,rn}为条件属性,故障类型D={d1,d2,…,dn}为决策属性,决策表S={U,C∪D},U={u1,u2,…,ui,…,un}为风机状态历史数据集,其中ui为第i个样本。

笔者采用的数据集中,监测点的个数为106,即条件属性个数为106,所以R={r1,r2,…,rn},并且只分析一种故障,即决策属性的个数为1,所以D=d1。

定义6信息系统S={U,R,V,f},其中U代表实验数据记录集,R=C={c1,c2,…,c106},V=D,f:U×R→V为一信息函数,表示对每一个a∈R,x∈U,f(x,a)∈Va。

定义7若P∈R,P≠φ,则P中所有等价关系的交集称为不可分辨关系或者是不可区分关系,记为IND(P);IND(P)={(x,y)∈U×U,r∈P,f(x,r)=f(y,r)}。

定义8S={U,C∪D}为一个决策表,其中C为条件属性集,D为决策属性集,C∩D=φ,决策表S的区分矩阵被定义为Cij,其中元素Cij={a∈C|a(xi)≠a(xj),且xi,xj满足陈述W(xi,xj)},W(xi,xj)表示((xi∈Posc(D)∧xj∉PosC(D))∨(xi∉PosC(D)∧xj∈Posc(D))∨(xi,xj∈PosC(D)∧(xi,xj)∉IND(D))

2.3 算法步骤

首先利用粗糙集的基于可辨识矩阵和逻辑运算的条件属性进行约简处理,得到的是最小约简集,再约简掉不必要属性,就能够获得最小的决策表(见Step1～Step6)。然后使用关联规则经典算法——Apriori算法进行关联规则挖掘(见Step7,Step8),生成最小决策表上大于支持度阈值的频繁项集,并在频繁项集的基础之上生成决策表上不小于置信度阈值的强关联规则。

Step1 对数据进行预处理,得到布尔型决策表S;

Step2 将决策表的可辨识矩阵CD进行计算;

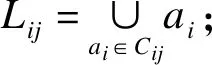
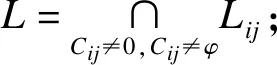
Step6 将约简结果输出,得到新的决策表。

Step7 扫描新的决策表,得到频繁1-项集,然后通过频繁1-项集得到频繁2-项集,如此进行下去,频繁k-项集通过连接得到频繁k+1-项集,然后通过将不满足支持度阈值的项删去,完成剪枝;

Step8 通过扫描频繁项集,将满足置信度阈值的规则输出,得到强关联规则。

3 实验分析

3.1 实验过程

风力发电机设备本身结构复杂,通常一台风力发电机的传感器就多达200个,所以其故障种类较多,表2中给出了21种典型的故障代码和故障名称,笔者选取故障码为T_158的故障为研究对象。对于其余故障的分析同158号故障分析的方法相同。

3.1.1 数据选择和属性编号

选取3 089条风机状态历史数据,即U={u1,u2,…,u3 089}进行分析,数据选择包括属性选择和抽样选择。对于数据选择,首先删除一些测量结果明显有误的数据,随机对数据进行抽样；然后对各个属性进行编号,A={a1,a2,…,ak,…,a139},其中ai表示第i个属性。对于属性选择,在原始数据中,有139个属性,将一些明显与风机状态没有关系的参数删去,例如故障警报、线圈匝数、版本号等等,剩余106个参数。经过初步的处理后,得到的风机状态历史数据记录为1 206条,即U={u1,u2,…,u1 206},106个属性,即A={a1,a2,…,a106}。

3.1.2 数据预处理

为了方便使用差别矩阵对决策表进行约简以及关联规则挖掘,需要将风机的参数转换为参数的取值只有0或1的布尔类型数。风机工作时,有些参数的取值在一定范围内波动,但有些参数的取值保持不变。因此,笔者对数据分类如下处理。

(1)波动型参数

对于该种特定的参数,专家根据经验设定针对该参数的阈值limit,假设A1在t1时候的取值为preValue,A1经过处理后取值为value1,则

(1)

其中,笔者取preValue的绝对值|preValue|,该参数在风机状态历史数据库中该参数的最大值为max,该参数在历史数据中的最小值为min。但取值为1表示该参数当前值超出了该参数的正常取值范围;0的value表示该参数当前值为正常。

(2)恒定型参数

对于一些取值恒定的参数,该参数的取值稍微偏离恒定值时并不是异常,只是该种参数允许波动的范围要小于波动型参数,笔者设定该种参数的允许波动值limit,设定恒定型参数的稳定值point,当前状态参数的取值为preValue,经处理后参数的取值为value2,则

(2)

(3)属性约简

使用粗糙集理论对条件属性集A进行约简,约简后得到AR为条件属性集合A的子集。笔者使用基于差别矩阵的属性约简算法,将算法实现过程分为三个步骤:首先得到区分矩阵,然后是求和操作,即将区分矩阵中的单一属性元素合并起来,最后约简得到最终结果。

3.1.3 关联规则挖掘

将粗糙集理论筛选出来的属性对应的数据取出,然后使用关联规则挖掘这些数据中的知识。根据相关专家根据经验以及最终与风机故障相关参数的个数确定关联规则的置信度和支持度,其中支持度为0.85,置信度为0.7,得到最终的关联规则R。

3.2 实验结果

使用一个传统的模型与笔者所建立的模型进行比较。所谓的传统模型就是使用相关性分析和关联规则的模型,该模型首先通过相关性分析将与决策属性,通过计算风机参数和故障类型之间的相关系数,将相关性小的参数删去,从而完成属性约简,形成新的决策表,然后使用关联规则对新的决策表进行挖掘[14-15]。

利用笔者所建立模型得到的规则进行故障诊断,如果规则成立,说明风机发生的是158号故障,即变频器加热器过载,并与传统模型进行比较,比较结果如表3所示。其中,0表示没有故障,1表示有故障。在准确度上,传统模型的准确度为54.56%,笔者所提出模型的准确率为65.78%。

表3 测试结果(部分)Table 3 The test result(part)

图2描述了笔者提出的模型的准确度,实心圆表示选用模型得到的结果与实际结果一致,空心圆代表选用模型结果与实际结果不一致。由此可见,图2中实心圆的密度反映了模型的准确度,密度越大,准确度越高;相反,空心圆的密度越高,准确度却越低。

图2 改进模型预测准确点与误判点Fig.2 Accuracy points and error points of improved model

改进模型与传统模型相比在准确度上有较大的提升,但还需要和实际值进行比较,其比较结果如图3所示。

图3 实验结果比较Fig.3 Comparison of experimental results

图3中,实线表示实际值,实线为0表示实际没有发生故障;实线为1表示发生了故障。虚线表示改进模型取值。实验结果表明在发生故障后(实线为1的部分),误判率比较高;在没有故障发生的时候(实线为0的部分),误判率较低。这表明本文提出的模型,没有故障发生时误判率比较低,但是真正发生故障后,误判率比较高。

4 结 论

(1)笔者提出了一种基于粗糙集属性约简和关联规则算法的风机故障诊断模型,该模型的特点是在挖掘关联关系的时候先进行了基于粗糙集的参数约简;与基于关联规则的方法相比较,虽然参数减少了,但是准确度提高了;解决了传统的仅基于关联规则的风机故障诊断模型的算法效率低,准确度不高等问题。

(2)笔者所提出的模型的优势在于实现使用了粗糙集理论中的属性约简算法,找到了特征属性子集,该集合能够完全表征原来属性的空间,即该属性子集能够完全替代原来的属性集合,然后使用关联规则算法,由于属性的数量与未处理之前大大减少,因此大大缩短了关联规则挖掘的时间。

(3)该模型明显优于传统的风机故障诊断模型,尤其是对大型风机状态历史数据的处理效果会非常显著;对于系统比较复杂,参数比较多的设备进行故障诊断的时候,并不是参数选取越多,其准确度就越高。