不锈钢-碳素钢筋混合配筋混凝土空心墩柱抗震性能研究
2021-11-08徐春一李佳莹
徐春一,李佳莹,牛 奔,佟 舟
(1.沈阳建筑大学土木工程学院,辽宁 沈阳 110168;2.中国建筑第六工程局有限公司天津轨道交通分公司,天津 300000;3.沈阳城市建设学院土木工程系,辽宁 沈阳 110167)
钢筋锈蚀已成为工程结构中的重大安全隐患,从根本上解决混凝土结构中钢筋锈蚀的方法值得关注。因不锈钢筋与碳素钢筋的力学性能相近,故用不锈钢筋代替碳素钢筋可有效解决目前钢筋锈蚀的问题。但不锈钢筋造价相对较高,利用不锈钢筋与碳素钢筋混合配筋的方式可满足经济需求,因此对混合配筋的混凝土结构进行研究,特别是对地震作用下的行为研究是十分必要的。
近年来,针对不锈钢筋的研究大多集中在其自身耐腐蚀性能及混凝土构件的力学性能等方面,对不锈钢筋混凝土构件抗震性能的探究较少,阻碍了不锈钢筋混凝土结构的推广应用。现有研究表明不锈钢筋防锈蚀能力强、延性高[1-5],较普通钢筋构件而言,不锈钢构件的耗能能力更好且承载力较高[6-8]。国内外已有研究证明了混合配筋的可行性[9-12],可见混合配筋形式在建筑结构中具有较好的应用前景,为不锈钢筋和碳素钢筋混合配筋混凝土结构的抗震性能研究奠定了基础。由于国内对混合配筋混凝土结构的抗震性能研究较少,因此笔者采用混合配筋方式对混凝土空心墩柱的受力性能进行模拟,对比全碳素钢筋、不锈钢-碳素钢筋混合配筋混凝土空心墩柱的抗震性能。并通过扩大试件参数对混合配筋混凝土空心墩柱的抗震性能展开进一步分析。
1 奥氏体不锈钢S30408的本构关系试验
1.1 奥氏体不锈钢筋S30408室温单向拉伸试验
试验选用钢筋有3种,具体试件参数见表1。

表1 拉伸试验试件设计Table 1 The test piece design for tensile testing
试验室温度设在(23±0.5)℃,拉伸试验的荷载通过施加力和引伸计一同控制。当塑性应变小于等于0.2%时采用应变片读数,塑性应变大于0.2%时采用位移计读数。试验过程中,“颈缩”现象明显。试件破坏方向和拉伸方向大致成45°。3种直径的不锈钢筋应力-应变曲线大体相似,由应力-应变曲线可以得出,不同直径的不锈钢筋从开始加载到试验结束均分为弹性阶段、强化阶段、劲缩阶段等[13-14]。
1.2 奥氏体不锈钢筋S30408本构关系模型的确定
通过拉伸试验分析可得,奥氏体不锈钢筋S30408应力-应变曲线呈非线性变化,没有明显屈服。选取3种不同直径的不锈钢筋试件,对已有的Ramberg-Osgood模型、Rasmussen模型、Gardner-Nethercort模型、Quach模型进行对比,不同模型下S1、S4和S10的应力-应变曲线如图1所示。


图1 不同直径的S30408应力-应变曲线对比Fig.1 Comparison of stress-strain curves of S30408 with different diameters
就整体应力-应变曲线来看,Quach模型偏差最小,且精度较高,可用做奥氏体不锈钢筋S30408的本构模型。因此,将Quach模型用于本次模拟研究中。Quach模型中不锈钢应力-应变公式如下:

式中:
2 有限元模型的建立
2.1 试件参数
为对比两种配筋形式下模型的抗震性能,设计两种试件:一个为全碳素钢筋试件(与文献[15]中试验试件设计相同参数);另一个为不锈钢筋-碳素钢筋混合配筋试件。桥墩模型的截面高宽为0.5 m×0.36 m,壁厚为120 mm。试件尺寸与配筋参数见图2和表2。

图2 试件尺寸与配筋Fig.2 Size and reinforcement of test piece

表2 试件参数Table 2 Parameters of test pieces
2.2 本构关系
模拟采用C40混凝土,混凝土采用塑性损伤模型。其单轴应力-应变曲线选用《混凝土结构设计规范》(GB 50010—2010)中提出的单轴应力-应变曲线[16]。碳素钢筋采用双折线弹塑性模型,不锈钢筋选用Quach模型。
2.3 有限元建模
混凝土采用三维实体单元C3D8R,钢筋选择三维桁架单元T3D2。以混凝土空心墩柱作为研究对象,建立有限元模型。为研究配筋形式对混凝土空心墩柱抗震性能的影响,建立两个墩柱模型,分别赋予不同钢筋骨架:碳素钢筋试件Z1;外层为不锈钢筋,内层为碳素钢筋试件Z2。模型中分别对两种配筋形式下柱顶的侧面施加往复位移,柱顶施加恒定竖向荷载。加载程序见图3。

图3 加载位移时程Fig.3 Loading displacement time history
2.4 模型验证
采用文献[15]中普通钢筋混凝土空心桥墩抗震性能研究的试验结果验证文中模型的适用性。Z1的模拟结果和文献[15]中试验对比结果见图4。可以看出,模拟试件的滞回曲线与试验滞回曲线基本吻合。因此建立的有限元模型能有效模拟钢筋混凝土矩形空心桥墩抗震性能。

图4 普通碳素钢筋试件数值模拟与试验结果对比Fig.4 Comparison of numerical simulation and test results for common carbon steel specimen
3 不同配筋形式下混凝土空心墩柱抗震性能分析
为分析不锈钢筋与碳素钢筋在混凝土空心墩柱中的协同工作性能,笔者对两种配筋形式的混凝土空心墩柱进行模拟,并对试件的破坏形式、滞回性能、承载力、刚度退化及耗能特性等抗震性能进行对比分析。
3.1 应力云图
两种模型试件的Mises云图如图5所示。由图可知,各墩柱的破坏均最先发生在柱最底端,随往复位移次数增加,应力最大部位向柱顶移动。

图5 Z1、Z2试件及钢筋骨架应力云图Fig.5 Stress plots of Z1、Z2 and reinforcement skeleton
3.2 滞回曲线与骨架曲线
Z1、Z2的滞回曲线和骨架曲线如图6、图7所示。由图可知,加载初期试件处于弹性阶段,初始刚度变化不大,随着加载层级增大,滞回曲线发生倾斜,且倾斜程度逐渐加大,说明试件承载能力不断衰减,刚度逐渐降低。Z1屈服荷载和屈服位移相对较小,但进入屈服阶段后,Z1的滞回环相比Z2饱满,达到破坏强度后,因不锈钢筋弹性模量小、变形大,Z2的骨架曲线下降,刚度退化较快。

图6 Z1、Z2滞回曲线Fig.6 Hysteresis loop of Z1 and Z2

图7 Z1、Z2骨架曲线对比Fig.7 Skeleton curves comparison of Z1 and Z2
3.3 承载力
通过试件的骨架曲线得到试件Z1、Z2的不同阶段荷载结果见表3。从表中可以看出,Z2的屈服荷载比Z1提高了49.55%,同时Z2的极限荷载较Z1增大了41.47%。说明配置不锈钢筋对于试件的屈服荷载和极限荷载都有提高,且对屈服荷载的影响更显著。

表3 试件不同阶段的荷载数据Table 3 Load data of each specimen at different stages
3.4 刚度退化
两种配筋形式下试件的刚度退化曲线如图8所示。从图中可以看出,在往复位移加载过程中,试件的刚度随加载位移的增加而逐渐降低。Z2的初始刚度较大,在加载初期刚度退化较快,随着加载层级增大,试件的残余变形逐渐积累,试件的刚度下降程度越来越平缓,最后两个试件的刚度相差不大。

图8 两种配筋形式下试件刚度退化曲线Fig.8 Stiffness degradation curves of components
3.5 耗能能力
为了研究试件的耗能能力,采用等效黏滞阻尼系数he来表示试件的耗能能力。耗能计算简图见图9,he表达式如下:

图9 试件耗能计算简图Fig.9 Sketch of specimen energy consumption calculation
(2)
(3)
式中:E为能量耗散系数;he为等效黏滞阻尼系数;S(ABC+ADC)为图中滞回环面积;S(OBE+ODF)为图中三角形面积。
各试件在不同加载周期的等效黏滞阻尼系数见表4,其中第1~4周期表示试件屈服前的周期,第5~8周期表示试件屈服后的周期。随着加载位移的增加,各试件对应的等效黏滞阻尼系数变化曲线见图10。

表4 试件等效黏滞阻尼系数Table 4 Equivalent viscous damping coefficient of specimens

图10 等效黏滞阻尼系数增长曲线Fig.10 The building-up curves of equivalent viscous damping coefficient
由图10可知,加载过程中,两试件等效黏滞阻尼系数变化曲线均呈先上升后下降的趋势。屈服前,Z1、Z2耗能能力大致相同;屈服后,Z2的等效黏滞阻尼系数大于Z1。说明混合配筋试件Z2具有比全碳素钢筋试件Z1更好的耗能能力。
综上可得,混合配筋能提高试件的承载力和耗能能力,而对刚度影响不大。故利用不锈钢筋与碳素钢筋在混凝土结构中的协同作用,可以满足抗震要求。
4 混合配筋混凝土空心墩柱抗震性能影响因素分析
通过有限元模拟得出,采用共同配置不锈钢与碳素钢筋这一配筋形式对混凝土结构抗震方面的研究是可行的。在此基础上,分别从高宽比、轴压比、纵筋配筋率等参数分析试件的骨架曲线、承载能力和延性等,对不锈钢-碳素钢筋混凝土空心墩柱的抗震性能展开进一步研究。
4.1 高宽比
高宽比在4~10变化时混合配筋墩柱S1、S2和S3的骨架曲线如图11所示。从图中可以看出,随着高宽比的增加,试件的屈服荷载下降,水平承载力降低,即试件的抗震性能与高宽比呈负相关。

图11 S1、S2和S3骨架曲线Fig.11 Skeleton curves of S1、S2 and S3
试件的承载力和位移延性系数(即试件在侧向力作用下破坏位移与屈服位移的比值)见表5。当高宽比介于4~8时,随着高宽比的增大,试件承载力呈下降趋势,而延性显著提升,当高宽比在8~10时承载力持续下降,延性几乎没有变化。显然较大的高宽比并不利于结构抗震。

表5 试件承载力和延性系数Table 5 Bearing capacity and ductility coefficient of specimens
4.2 轴压比
轴压比在0~1变化时不同混合配筋混凝土空心墩柱骨架曲线如图12所示。

图12 S2、S4~S6试件骨架曲线Fig.12 Skeleton curves of S2 and S4~S6
从图中可以看出,随着加载位移的增大,纵向钢筋发生屈曲同时混凝土剥落,荷载-位移曲线出现下降段,且轴压比越大,对下降段的下降幅度影响越明显。
试件的承载力和位移延性系数见表6。从表中可以看出,当轴压比在0.5~0.7时,随着轴压比的增大,试件的承载力迅速提升,延性系数增大即延性有所提高;当轴压比超过0.7时,试件的承载力呈下降趋势,延性系数也缓慢减小。说明轴压比对试件的承载能力影响显著,对延性影响不大。

表6 试件承载力和延性系数Table 6 Bearing capacity and ductility coefficient of specimens
4.3 纵筋配筋率
纵筋配筋率在1%~6%变化时不同混合配筋混凝土空心墩柱骨架曲线如图13所示。从图中可以看出,纵筋配筋率在1.5%~4.3%时,试件的水平承载力有所提高;当纵筋配筋率大于4.3%时,试件的水平承载能力下降。说明纵筋配筋率超过一定范围时,不利于试件的抗震性能。
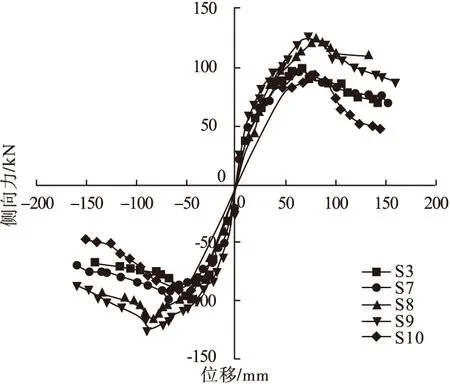
图13 S3、S7~S10试件骨架曲线Fig.13 Skeleton curves of S3 and S7~S10
试件的承载力和位移延性系数见表7。从表中可以看出,延性系数起初呈增大趋势,试件的承载力显著提高。当纵筋配筋率大于4.3%时,试件的延性基本不变。故在纵筋配筋率介于1.5%~4.3%时,纵筋配筋率越高,试件的承载力越大,刚度退化越慢,变形能力越好。

表7 试件承载力和延性系数Table 7 Bearing capacity and ducitility coefficient of specimens
5 结 论
(1)通过数值分析对两种配筋形式进行研究发现,混合配筋混凝土空心墩柱承载力较碳素钢筋混凝土空心墩柱承载力提高了41.47%,耗能能力也有所增强,而刚度变化大致相同。说明混合配筋可有效提高混凝土空心墩柱的综合抗震性能。
(2)改变高宽比对混合配筋混凝土空心墩柱的承载力及延性影响显著,高宽比宜在4~8,较大的高宽比并不利于结构抗震。不同轴压比对试件的承载能力影响显著,对延性影响不大,轴压比宜控制在0.5~0.7。同时控制纵筋配筋率在1.5%~4.3%时,适当提高纵筋配筋率可改善不锈钢-碳素钢筋混凝土空心墩柱的抗震性能。
