一种基于航拍无人机的高桥墩偏位检测方法
2021-11-08焦华成吴春利陈江川王子琳
焦华成, 吴春利, 陈江川, 周 森, 王子琳
(吉林大学, 长春 130000)
高桥墩偏位是桥梁安全的重大隐患[1]。当高桥墩出现偏位时,高桥墩受力位置不再位于高桥墩截面中心,会出现偏心受力,这将继续加大高桥墩偏位,致使桥梁逐渐丧失稳定性,直至破坏[2]。高桥墩偏位是评估桥梁是否安全的一个重要技术指标,因此,对使用中的高桥墩进行偏位检测极为重要[3]。常规检测方式,先通过目测发现可能出现偏位的高桥墩[4],后对有偏位嫌疑的高桥墩进行人工偏位检测,这既需耗费大量人力,且检测区域有限,又难以高效准确地对高桥墩进行检测[5]。因此,在高桥墩偏位检测领域,急需一种安全、快捷、机动性强、适应性强的检测手段[6]。为解决这一难题,本文提出了一种基于航拍无人机的高桥墩偏位检测方法,此方法能够快速对高桥墩进行偏位检测。
1 航拍无人机
航拍无人机爬升力较强,高度控制灵活,在短时间内能够完成从低海拔爬升至几百米高空的飞行任务,也能够进行50 m以内的超低空拍摄。航拍无人机在操控上极为方便,起飞降落受场地空间限制较小,在操场、公路或其它较开阔的地面均可起降。无人机小型轻便、机动灵活、稳定性和安全性好。
此前,航拍无人机多用于摄影、新闻、测量、地质勘察等方面,对于高桥墩偏位这种需要高精度数据且受外界环境影响较大的领域,航拍无人机的应用仍是一片空白。
目前,航拍无人机已能在4级风力的影响下平稳拍摄图片。随着卫星定位系统不断升级,新型航拍无人机已能直接显示出拍摄时的镜头与拍摄点的水平面夹角。在扣除相应夹角后,可认为拍摄时的镜头是绝对水平的。高桥墩偏位检测就是运用无人机的这项功能进行航拍。工作时无人机需与终端设备(手机、电脑、iPad等)连接,并通过终端设备控制飞行。飞行时的数据(飞行高度、倾斜角度等)可在终端设备的显示屏直接展示。
2 无人机航拍过程
1) 对无人机进行开机处理,放置在合适位置,注意来往车辆。案例中放置在高桥墩的正前方。
2) 调试终端设备,将终端设备与无人机连接,检查连接情况,确认GPS信号是否满足飞行要求,并测试设备是否正常。
3) 进行高桥墩偏位检测。所在城市当中无法找到高度20 m以上的高桥墩,案例中以15 m的高桥墩为例。
(1) 将已开机的无人机放置在高桥墩正面。
(2) 终端设备按步骤调试正常后,控制无人机上下飞行,飞行中不能左右摆动(高桥墩附近一般为空旷地带,无人机无需规避障碍,能够竖直飞行),无人机从地面飞行到高桥墩顶部。
(3) 飞行过程中,每隔一段相等距离拍摄一张图片,确保高桥墩每一部分都能被拍摄下来。
(4) 案例中,将无人机放置在高桥墩的正前方2 m处,竖直方向自下而上每隔1 m拍摄一张图片,共拍摄15张图片。
3 航拍图片的处理
3.1 图片前期处理
1) 根据终端设备屏幕显示的倾斜角度,并按屏幕提示的旋转方向将图片旋转相应的倾斜角度。处理完后,可认为图片拍摄时镜头处于水平位置,以减小因航拍无人机抖动而产生的误差。
2) 在高桥墩最底部拍摄的图片底部建立坐标,x坐标与图片底部重合,坐标原点在底部桥墩的中点[7],坐标系如图1所示。

图1 高桥墩底部第1张图片坐标系建立
拍摄过程中,只允许航拍无人机上下移动。因此,在第1张图片的坐标轴确定后,其余图片的y轴与第1张图片的y轴重合,x轴则依次向上平移,按等间距拍摄相邻图片的高差段即可。案例中依次向上平移1 m。
3.2 航拍图片中高桥墩中轴线的拟合[8]
1) 偏位高桥墩中轴线在已定坐标系下的中轴线方程
高桥墩偏位时,支座处力的作用点将发生变化,由高桥墩中心向边缘偏移[9]。根据弹性力学原理,支座处力的作用面可视为小边界,因此,运用圣维南原理,将模型进行简化,如图2所示。
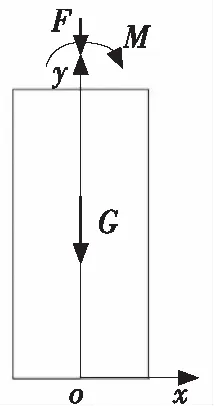
图2 高桥墩受力模型
当支座施加在高桥墩顶部竖直向下的力F与自重G单独作用时,只能引起高桥墩的竖向沉降,弯矩M是引起横向偏移的主要原因。下面根据弹性力学对高桥墩中轴线方程进行推导。
根据矩形梁受纯弯曲时,应力分量表达式得:
(1)
代入物理方程得:
(2)
代入几何方程得:
(3)
对x和y积分得:
(4)
式中:f1和f2分别是x和y的待定函数;u和v是模型中轴线纵向和横向的位移;I是模型横截面惯性矩。
将式(4)代入式(3)中的第3式得:
(5)
将式(5)移项得:
(6)
从式(6)可以看出,等式左边只是y的函数,而等式右边只是x的函数。若想要等式(6)成立,则两边都等于同一常数ω,代入式(6)得:
(7)
对式(7)积分得:
f1(y)=-ωy+u0
(8)
(9)
将式(8)、式(9)代入式(4)得:
(10)
(11)
根据位移边界条件:
(12)
式中:h为模型高度。
将式(12)代入式(10)和式(11)得:
u0=0
(13)
(14)
联立式(14),解得:
(15)
将式(15)代入式(10)和式(11)得:
(16)
将x=0代入式(16)的第2式得:
(17)
式中:v是模型中轴线的横向位移。

2) 航拍图片中高桥墩中轴线的拟合
(1) 图片的二值化处理
对彩色图片灰度化后,把获取到的灰度图像进行二值化处理。即将目标用户背景分类,为后续的识别做准备。二值化方法采用阈值法,它利用图像中目标与背景的差异,把图像分别设置为2个不同的级别,通过选取一个合适的阈值,确定某像素是目标还是背景,从而获得二值化的图像。
(2) 使用Matlab对桥墩边界进行识别,提取像素点坐标
将二值化处理后的图片导入Matlab,并对高桥墩边界像素点进行检索,提取每行像素的边界点坐标。
(3) 高桥墩中轴线像素点坐标的确定
高桥墩采用对称式设计,中轴线应位于左右边界连线中点处。对每行边界像素点的横坐标取平均值,得到中轴线像素点的横坐标。中轴线像素点的纵坐标与相应边界像素点纵坐标相同,从而确定中轴线像素点坐标。
(4) 高桥墩中轴线方程的拟合
中轴线像素点坐标已知,所有像素点依次连成一条曲线,即为高桥墩中轴线[10]。已知高桥墩中轴线方程为二次方程,运用Matlab对中轴线进行二次方程拟合,拟合形式为:y=ax2+bx+c。
3) 坐标轴的等价转换
高桥墩中轴线拟合后,每张图片在自身的坐标系下都有一个中轴线方程,即每段高桥墩的中轴线方程。
每张图片都有一个坐标系,每个坐标系只有x轴移动,y轴没有移动[11],即x轴上下移动。因此,轴线方程中只有c值变化。每张图片中轴线方程形式为:y=ax2+bx+c,理论上每张图片中的a值和b值应相等,c值不同,c值不同代表图片所处的位置不同。
每张图片处理时有偶然误差,为减小偶然误差,对所有图片的a值和b值进行如下平均处理:
(1) 每张图片中的中轴线方程进行求导后,为y′=2ax+b。

3.3 高桥墩偏位角度的计算
得到高桥墩中轴线方程后,对轴线方程求导,得到中轴线方程的切线方程,代入边界条件求出斜率后,进行反三角函数运算,可求出高桥墩的偏位角度[12]。
4 航拍图片实际处理过程
以15 m高桥墩为例,从下而上共拍摄15张图片,以其中一张图片举例说明。
4.1 图片的二值化处理
调整图片阈值为180,高桥墩与图片背景因颜色不同而分离,如图3所示。

图3 二值化处理示意
4.2 边界点像素点坐标的提取
将二值化处理后的图片导入Matlab,对高桥墩边界像素点进行检索,提取每行像素的边界点坐标,如图4所示。
4.3 中轴线像素点坐标的确定
对每行边界像素点的横坐标取平均值,得到中轴线像素点的横坐标。中轴线像素点的纵坐标与相应边界像素点纵坐标相同,从而得到中轴线像素点坐标,如图5所示。

图4 边界像素点提取示意

图5 中轴线像素点坐标
4.4 高桥墩中轴线方程的拟合
1) 先旋转中轴线,后拟合
中轴线接近90°,拟合时a值很大,轴线方程类似指数方程,拟合结果会有较大误差。为了减小误差,将轴线进行90°旋转后拟合,如图6所示。
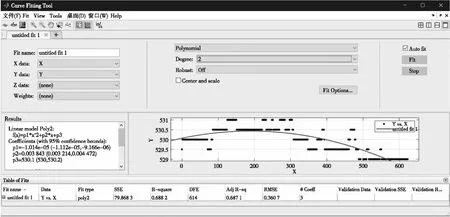
图6 中轴线拟合
2) 拟合后中轴线方程的a、b值
根据图6,该图片中高桥墩中轴线方程为:
y=-1.014×10-5x2+3.843×10-3x+c
同理可得其它14张图片中的中轴线方程,其a、b值如表1所示。
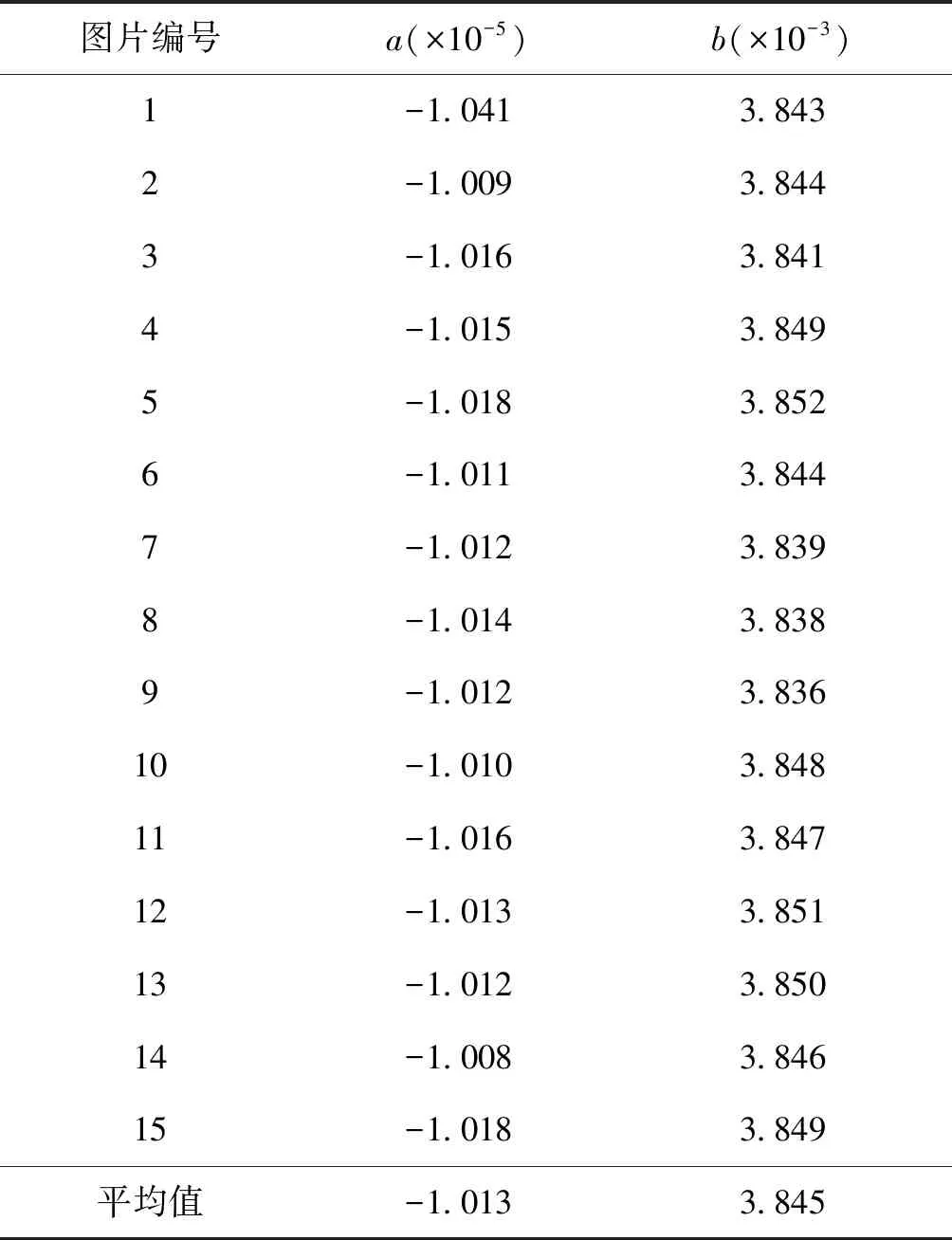
表1 15张图片中中轴线方程的a、b值
3) 根据中轴线方程求中轴线偏位角度
(1) 根据表1列出整体中轴线方程
y=-1.013×10-5x2+3.845×10-3x+c
(18)
(2) 对整体中轴线方程求导
y′=-2.026×10-5x+3.845×10-3
(19)
(3) 求中轴线偏位角度
工程上以高桥墩底部偏位角度为技术标准,因此,将x=0代入式(19)得:
y′=3.845×10-3
已知x=0处中轴线的斜率,进行反三角函数运算得出角度。
tan-13.845×10-3=0.22°
偏位角度为0.22°,该高桥墩偏位符合要求。
整个图片的处理过程,编写成一套Matlab程序处理。当无人机航拍完一组图片后,将图片导入程序,便能快速准确得到结果[13]。
5 精度检验
受条件限制,无法通过室外试验来检验该方法的精度,因此,通过室内试验进行检验。
5.1 运用CAD软件模拟高桥墩偏位后的正面图,并借助软件求出偏位角度
在CAD软件中画出高桥墩模拟图,偏位角度设置为5°,在高桥墩底部建立坐标,如图7所示。

图7 高桥墩模拟
实际工程中,偏位角度很小[14]。但角度过小不利于精度检验,为了提高精度,将正面图的偏位角度适当放大[15]。
5.2 运用本文方法对正面图进行处理,求出中轴线偏位角度
运用上文所述的方法,将图7进行处理,模拟出中轴线方程,如图8所示。
中轴线方程为:
y=4.498×10-5x2+8.248×10-2x+c
(20)
中轴线切线方程为:
y′=4.498×10-5x+8.248×10-2
(21)
中轴线偏位角度为:
tan-18.248×10-2=4.72°
5.3 误差比较
根据上述计算可知,真实角度为5°,计算结果为4.72°,则精度为:
(5-4.72)÷5=5.6%
本方法计算出的结果与真实角度的误差为5.6%,精度较高[16]。

图8 中轴线方程模拟
6 结论
1) 本文提出的基于航拍无人机的高桥墩偏位检测方法已成功应用于长春三号线的桥墩检测,工程应用检测快速、结果准确。
2) 试验结果表明,此方法所计算出的高桥墩偏位角度与真实偏位角度偏差不超过6%,符合工程要求。
3) 目前,此方法相较常规检测方法更能准确、高效、快速地进行大范围的高桥墩偏位检测,适宜推广。
4) 未来几年,随着航拍无人机技术的不断升级,拍摄将更加稳定、准确,检测精度将大大提高。
