异质无线传感器网络中d-鲁棒强连通控制吸收集的构造
2021-11-08张伟光黎昌珍梁家荣梁新宇
张伟光,黎昌珍,梁家荣,梁新宇
(1.广西大学 计算机与电子信息学院, 广西 南宁 530004; 2.广西大学 公共管理学院, 广西 南宁 530004;3.广西大学 电气工程学院, 广西 南宁 530004)
0 引言
无线传感器网络是由大量无线传感器结点所组成的网络。与有线网络相比,由于不需要搭建相关的物理基础设施,无线传感器网络具有部署快速,搭建灵活和成本低廉的优势。目前,无线传感器网络已被广泛地应用于环境监测,医疗健康,灾难救助和战场自动化等众多领域[1- 4]。
在无线传感器网络中,无线传感器结点的能量和信号传输范围都是有限的。当两个传感器结点之间的距离大于彼此的传输范围时,结点之间进行通信必然要通过多跳的方式让其他结点来转发信息。因此,在大型的无线传感器网络中,结点之间进行通信时,由于大量的信息交换和转发,极有可能造成信号之间的干扰和冲突,严重的情况下甚至有可能造成整个网络的崩溃。为此,EPHREMIDES等[5]提出在无线网络中构建一个虚拟骨干,结点之间进行通信时,信息只在虚拟骨干中进行转发和传输,也就是说,由虚拟骨干承担整个网络的通信功能。可以看出,虚拟骨干的大小(结点的多少)是衡量一个虚拟骨干性能的重要指标,较小的虚拟骨干往往有着更少的开销,从而延长整个网络的使用寿命。因此,如何寻找网络的最小虚拟骨干是一个关键的问题。
根据结点的信号传输范围是否相同,无线传感器网络可分为同质无线传感器网络和异质无线传感器网络。在同质无线传感器网络中,传感器结点都有着相同的传输范围。假设结点都分布在二维欧几里德平面上,那么一个同质无线传感器网络可以被建模成一个单位圆盘图,网络的一个虚拟骨干则对应于单位圆盘图的一个连通控制集。于是,求解同质无线传感器网络的最小虚拟骨干的问题可以被转化成求解单位圆盘图的最小连通控制集问题。然而,文献[6]中的作者证明了求解单位圆盘图的最小连通控制集问题是NP-hard的。因此,许多近似算法[7-11]被设计出来求解该问题的一个较小的近似解。由于在实际情况中,网络中的传感器结点的信号传输范围可能会有所不同,这样的无线传感器网络被称为异质无线传感器网络。由于单位圆盘图不能准确地刻画异质无线传感器网络,异质无线传感器网络通常被建模成一个圆盘图,网络的一个虚拟骨干则对应于圆盘图的一个强连通控制吸收集。由于单位圆盘图是圆盘图的一种特殊情况,因此,求解圆盘图中的最小强连通控制吸收集问题也是一个NP-hard的问题。于是,许多相关算法[12-15]都被设计来求解该问题的近似解。
在实际情况中,可能会发生传感器结点失效或结点信号传输范围改变等问题,从而有可能导致虚拟骨干失效。因此,虚拟骨干的鲁棒性也是一个不得不考虑的重要因素。为了解决结点失效导致虚拟骨干失效的问题,一个很好的解决方案是构建一个具有容错能力的虚拟骨干,这方面目前已经有了大量的研究成果[16-20]。然而,在传感器结点没有失效但是信号传输范围发生了改变的情况下保证虚拟骨干正常工作的相关研究较少。在文献[21]中,LIANG等在二维同质无线传感器网络中研究了这一问题,提出了d-鲁棒连通控制集的概念和计算d-鲁棒连通控制集的两个算法。受此启发,本文研究了在二维异质无线传感器网络中,当传感器结点的信号传输范围发生改变时保证虚拟骨干依旧有效的问题。针对该问题,本文提出了d-鲁棒强连通控制吸收集的概念以及计算其的一个近似算法d-SCDAS-C。
1 预备知识
假设在一个异质无线传感器网络中所有传感器结点都分布在二维欧几里德平面中,那么该网络所对应的圆盘图G=(V,E)可以通过以下方法得到:让V中结点的个数等于原网络中的结点个数,且V中每个结点都对应于原网络中的某个结点。对于任意结点v∈V,其信号传输范围用rv表示。对于任意一对结点u,v∈V,在原网络中u和v之间的欧几里德距离用dist(u,v)表示。如果以v为圆心,rv为半径的圆盘内存在另一结点u∈V,那么u和v之间会有一条从u到v的有向边(u,v)∈E。特别地,如果(u,v)∈E且(v,u)∈E,那么u和v之间有一条双向边。于是,G的边集E={(u,v)|u,v∈V, dist(u,v)≤ru}。为了便于理解,图1给出了一个具有6个结点的圆盘图。可以看出,圆盘图是一个有向图。
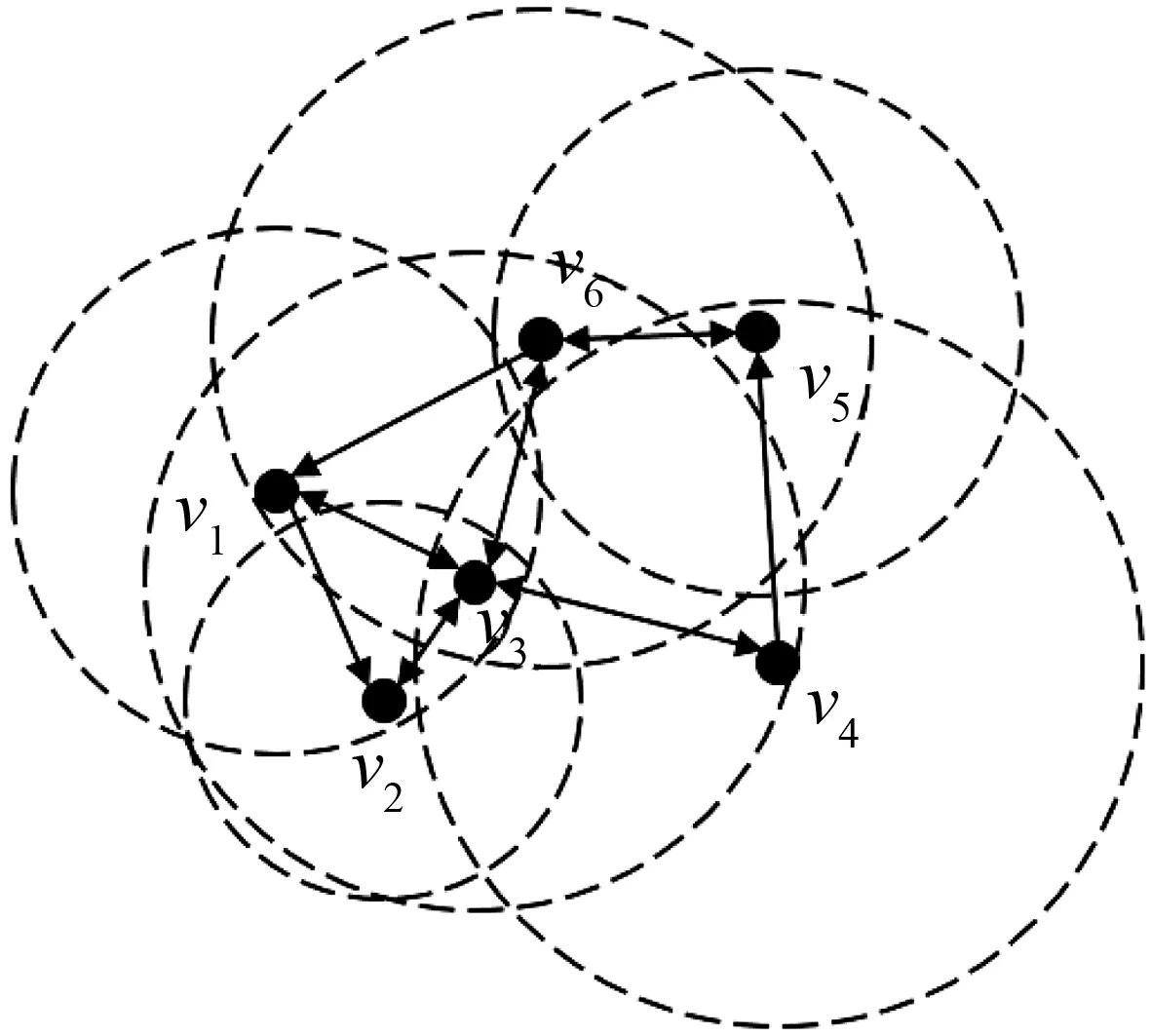
图1 一个具有6个结点的圆盘图
为了方便讨论,介绍一些相关的符号和定义。给定一个有向图G=(V,E),对于任意结点v∈V,N+(v)={u|u∈V,(v,u)∈E},N-(v)={u|u∈V,(u,v)∈E}。N+[v]=N+(v)∪{v},N-[v]=N-(v)∪{v}。对于集合S⊆V,G[S]表示由S导出的诱导子图,即G[S]=(V,{(u,v)|u,v∈S,(u,v)∈E})。N+(S)={u∉S|u∈N+(v),v∈S},N-(S)={u∉S|u∈N-(v),v∈S}。N+[S]=N+(S)∪S,N-[S]=N-(S)∪S。
定义1控制集和吸收集。在一个给定的有向图G=(V,E)中,如果点集S⊆V满足对于任意结点v∈V-S,存在结点u∈S使得边(u,v)∈E,则S被称为图G的控制集。如果S满足对于任意结点v∈V-S,存在结点u∈S使得边(v,u)∈E,则S被称为图G的吸收集。
定义2强连通。给定一个有向图G=(V,E),如果对于任意一对结点u,v∈V,在G中存在着从u到v和从v到u的有向路径,那么G是强连通的。
定义3强连通控制吸收集。在一个给定的有向图G=(V,E)中,如果点集S⊆V既是图G的控制集,又是G的吸收集,那么S被称为图G的控制吸收集。同时,如果诱导子图G[S]是强连通的,则S被称为图G的强连通控制吸收集。
定义4(1-d)-圆盘图。假设在一个给定的无线传感器网络N中所有的传感器结点都分布在一个二维欧几里德平面上,G=(V,E)是N所对应的圆盘图。给定一个参数d(0≤d<1),则G1-d=(V,E1-d)被称为N(或G)的(1-d)-圆盘图当且仅当E1-d={(u,v)|u,v∈V, dist(u,v)≤(1-d)ru}。
定义5d-鲁棒强连通控制吸收集。给定一个圆盘图G=(V,E),G1-d=(V,E1-d)是G的(1-d)-圆盘图。点集S⊆V被称为G的d-鲁棒强连通控制吸收集当且仅当S既是G的强连通控制吸收集,又是G1-d的强连通控制吸收集。
定义6独立集和极大独立集。对于一个给定的有向图G=(V,E),如果点集S⊆V满足对于任意一对结点u,v∈S,(u,v)∉E或者(v,u)∉E,那么S被称为图G的独立集。同时,如果对于任意结点v∈S,S∪{v}不再是独立集,那么S被称为图G的极大独立集。
2 d-鲁棒强连通控制吸收集构造算法(d-SCDAS-C)
本文所提出的d-鲁棒强连通控制吸收集构造算法(d-SCDAS-C)的输入包括:①圆盘图G=(V,E);②参数d(0≤d<1);③结点传输半径向量Vr;④结点距离向量Vdist。为了区分不同的结点,V中的每个结点都分配了一个唯一的ID,ID范围从1到|V|。用vi表示ID为i的结点,其传输范围记为ri。在算法的输入中,G要满足其所对应的(1-d)-圆盘图是强连通的。Vr是一个1×|V|的一维向量,Vr[i]=ri。Vdist是一个|V|×|V|的二维向量,Vdist[i][j]=dist(vi,vj)。于是,d-SCDAS-C算法的主要步骤如下:
① 根据G,d和Vdist构造辅助图G1-d=(V,E1-d),其中E1-d={(vi,vj)|vi,vj∈V,(vi,vj)∈E且dist(vi,vj)≤(1-d)Vr[i]}。
在步骤①中,对于给定的圆盘图G,参数d和结点距离向量Vdist,构造辅助图G1-d的算法(算法1)步骤如下:
Step 1:初始化,E1-d=φ,E′=E。
Step 2:在E′中任取一条边e=(vi,vj)∈E′(vi,vj∈V)。如果Vdist[i][j]≤(1-d)Vr[i],则E1-d=E1-d∪{e}。E′=E′-{e}。
Step 3:当E′=φ时,返回G1-d=(V,E1-d),算法结束。否则,返回step 2。
Step 1:初始化,V′={r}∪N+(r),E′={(r,v)|v∈N+(r)},T=(V′,E′),I={r},V″=V-V′。
Step 2:在N+(V′)∩V″中选取使得|N+(v)∩V″|最大时ID最小的结点v,I=I∪{v},E′=E′∪{(u,v)}∪{(v,x)|x∈N+(v)∩V″}(u是N-(v)∩V′中ID最小的结点),V′=V′∪N+[v],V″=V″-N+[v]。
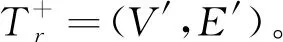
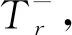
3 d-SCDAS-C算法的理论分析
本节主要内容包含对本文所提出的d-SCDAS-C算法的正确性分析和近似比分析。
首先分析其正确性,为此,先证明以下引理:
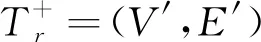

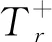

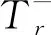
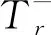
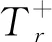
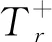
接下来证明d-SCDAS-C算法的近似比,为此,先证明以下引理:
引理3执行完算法2之后,I是图G1-d的极大独立集。
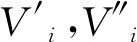
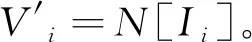
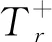
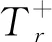
引理5给定一个无线传感器网络N,G=(V,E)和G1-d=(V,E1-d)分别是由N得到的圆盘图和(1-d)-圆盘图。令rmin,rmax分别表示N中结点的传输范围的最小值和最大值,OPT表示圆盘图G的一个最小强连通控制吸收集,I是G1-d的一个极大独立集,则|I|≤(ak2+ak+1)|OPT|,其中
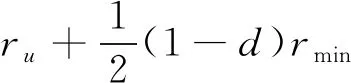
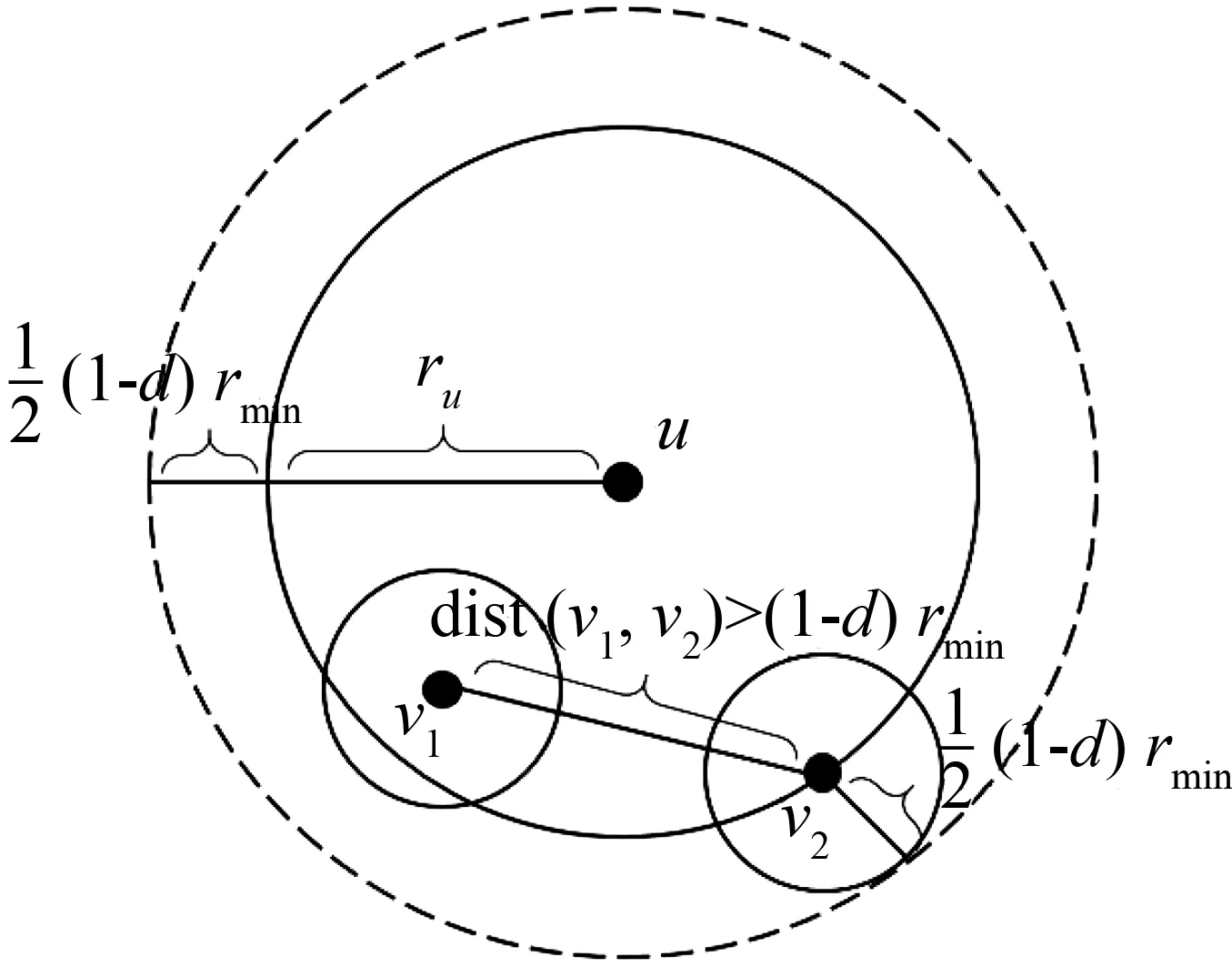
图2 引理5中关于Iu中结点个数上限的说明,其中v1,v2∈Iu。
因为ru≤rmax,所以有
因此,有
定理2令D表示算法d-SCDAS-C的输出,则|D|≤4(ak2+ak+1)|OPT|,其中,OPT表示圆盘图G的一个最小强连通控制吸收集,
rmin,rmax分别表示Vr中的最小值与最大值。
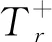
4 结语
本文研究了如何在二维异质无线传感器网络中构造带有鲁棒性的虚拟骨干网的问题。为此,提出d-鲁棒强连通控制吸收集的概念并给出了计算d-鲁棒强连通控制吸收集的近似算法d-SCDAS-C,其近似比为4(ak2+ak+1),其中
在未来,关于该问题的进一步研究工作主要有三点:一是利用相关的数学知识改进极大独立集的上界或是一个结点周围独立结点的个数的上界,从而改进算法的近似比;二是对算法进行优化或改进,或者提出新的算法,使得最终计算的d-鲁棒强连通控制吸收集与最优解之间的近似比更小;三是将该研究和算法拓展到三维空间中。
