平面近场声全息中指数滤波器窗函数设计优化

赵 晨，冯丹平，杨明明，高守勇

（91388部队95分队，广东 湛江 524022）

0 引 言

近场声全息技术（Near-field Acoustical Holography,NAH）是噪声源识别、定位、分析的一项重要技术。其基本原理是通过测量近场全息面的声场数据（如声压、振速、声强等），采用一定的近场声全息算法，反演重建声源面声场信息或者预测远场辐射声场信息[1]。根据测量面形状的不同，近场声全息技术分为平面近场声全息、柱面近场声全息和球面近场声全息[2-5]。其中基于声压测量的平面近场声全息技术，对于大型目标的噪声源分析更为适用，并已经应用于实际测量工作中。

平面近场声全息算法一直是声学领域研究的热点。常用平面近场声全息算法所采用的基本方法包括空间二维傅里叶变换法、边界元法、等效源法、统计最优法等[6-10]。基于空间二维傅里叶变换法的近场声全息（Near-Field Acoustic Holography Based on Spatial Two-Dimensional Fourier Transform,SFT-NAH）算法是近场声全息算法中的一种典型算法，通过将全息面上声压进行空间二维傅里叶变换再乘以格林函数，最后进行空间二维傅里叶逆变换得到重建面或者预测面声场信息。相比较其他方法，空间二维傅里叶变换法具有算法简单、不需要占用较大内存和计算速度快等优点。

采用空间二维傅里叶变换法进行近场声全息重建时，由于环境噪声、系统误差等因素的影响，对重建过程有重要影响的高波数域的倏逝波成分很容易被各类噪声误差淹没，导致重建结果产生较大误差。因此重建过程中必须进行波数域的低通滤波，指数滤波器是基于空间二维傅里叶变换法的近场声全息算法中常用的滤波方法[11]。该方法中有两个关键参数，分别是指数滤波器截止波数和指数滤波器窗函数陡度系数。这两个关键参数如果设置不合理就会严重影响指数滤波器滤波效果，进而影响近场声全息算法声场重建效果。因此对其进行设计优化，对于提高声全息算法的重建精度和分辨率具有重要意义。

本文以水下声全息技术应用为背景，以大孔径近场声全息面为分析模型，重点分析对应不同声源频率，指数滤波器窗函数及截止波数的取值对声全息重建误差的影响。相邻两声源相干引起的分辨率误差是近场声全息重建误差的一个主要来源，有效降低该误差是提高近场声全息算法精度的一项重要工作，因此选取两个相邻声源作为检测的对象，针对基于空间二维傅里叶变换法的近场声全息算法中指数滤波器的截止波数和窗函数陡度系数这两个关键参数，采用最小二乘法进行了设计优化。优化结果表明，有效提高了基于空间二维傅里叶变换法的近场声全息算法的重建精度和分辨率。

1 基于空间二维傅里叶变换法的近场声全息算法基本原理

由水声传播基本理论可知，在理想流体介质中，不依赖于时间变量的稳态声场的亥姆霍兹（Helmholtz）方程为

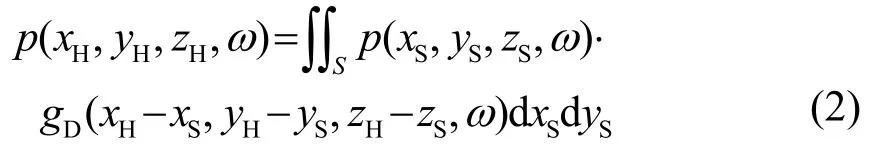
在狄利克雷（Dirichlet）边界条件下，格林函数为

对式（2）两边进行空间二维傅里叶变换，可得：

FFT-NAH的基本思想是由全息面声压分布矩阵对其做空间二维傅里叶变换，将其转化到波数域，经波数域滤波后乘以对应的格林函数矩阵，便可得到空间二维傅里叶变换后的重建面的声压分布矩阵，对其做空间二维傅里叶逆变换即可得到重建面声压分布。

2 指数滤波器

在近场声全息理论中，当全息面声压进行二维傅里叶变换后将其与对应指数滤波器相乘，以此来进行波数域滤波，是提高近场声全息算法重建精度的一种有效手段。本文在计算过程中首先对全息面声压数据进行二维傅里叶变换，然后与对应指数滤波器相乘进行波数域滤波，最后进行二维傅里叶逆变换得到重建面声压分布。

基于空间二维傅里叶变换法的近场声全息算法中常用的指数滤波器计算公式为[11]

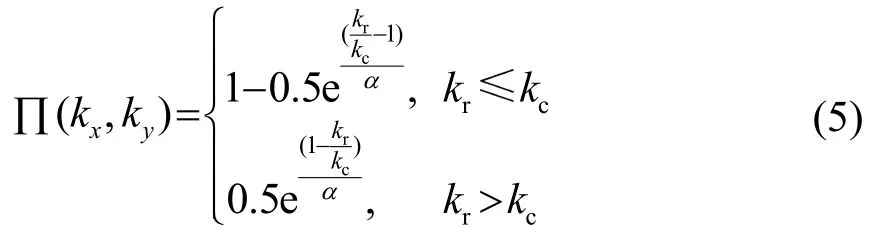
由式（5）可以看出，指数滤波器的设计有两个关键参数，分别是窗函数的陡度系数α和滤波器的截止波数kc。已有研究中，通常情况下指数滤波器窗函数陡度系数α的取值范围为0.1～0.2，指数滤波器截止波数kc经验公式为：kc=0.6π/Δ，Δ为全息面上的测量间隔，对于本文研究工作具有一定的参考意义。本文将针对窗函数的陡度系数α和滤波器的截止波数kc这两个关键参数的优化设计，采用最小二乘法分别进行仿真分析。

3 仿真分析

3.1 点声源及全息测量面模型建立

以频率为1 kHz、声源半径为0.01 m和间距为1.5 m的两个模拟点声源为声源模型进行仿真分析，结果如图1所示。同时，建立规模为50 m×50 m、测量间隔分别为 50 m和 255 m、距离声源中心面1 m的全息测量面仿真模型。以均匀分布噪声模拟环境噪声等各种噪声，模拟信噪比为20 dB时仿真全息测量面的测量效果如图2所示。

图1 模拟点声源声压传播图Fig.1 Sound pressure propagation diagram of simulated point sound source

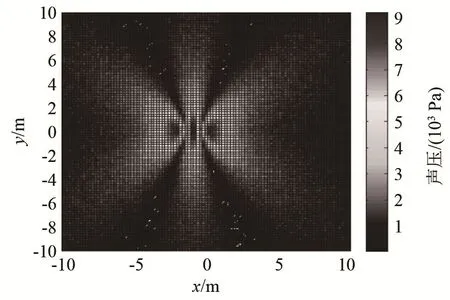
图2 模拟全息测量面测得声压分布图Fig.2 Sound pressure distribution diagram measured by simulated holographic measuring surface

通常情况下滤波器窗函数陡度系数α的取值范围为0.1～0.2，滤波器截止波数kc=0.6π/Δ，但通过仿真分析发现，当声源频率不同时，选择不同的滤波器窗函数陡度系数α和滤波器截止波数kc会有更优的反演效果。例如，当声源频率为1 kHz，时若α=0.12，kc=0.6π/Δ，则反演点声源声压传播图如图3所示。当声源频率为1 kHz，时若α=0.06，kc=0.3π/Δ，则反演点声源声压传播图如图4所示。

图3 声源频率为1 kHz，α=0.12，kc=0.6π/∆，反演点声源声压传播图Fig.3 The inversed sound pressure propagation diagram of 1 kHz point source for α=0.12 and kc=0.6π/∆

图4 声源频率为1 kHz，α=0.06，kc=0.3π/∆，反演点声源声压传播图Fig.4 The inversed sound pressure propagation diagram of 1 kHz point source for α=0.062 and kc=0.3π/∆

3.2 指数滤波器参数设计分析

定义p1为模拟点声源声压幅值分布，p2为反演点声源声压幅值分布。定义点声源声压反演结果的幅值误差为[12]

3.2.1 滤波器截止波数设计分析

α值为0.12时，分别取kcΔ/π的值为0.2、0.3、0.4、0.5、0.6、0.7、0.8、0.9，对相应的反演声源面声压分布效果对比分析如表1所示。

表1 α=0.12 时，kc∆/π 与 E 对应关系Table 1 The correspondence between kcΔ/π and E,when α=0.12

α值为0.15时，分别取kcΔ/π的值为0.2、0.3、0.4、0.5、0.6、0.7、0.8、0.9，对相应的反演声源面声压分布效果对比分析如表2所示。

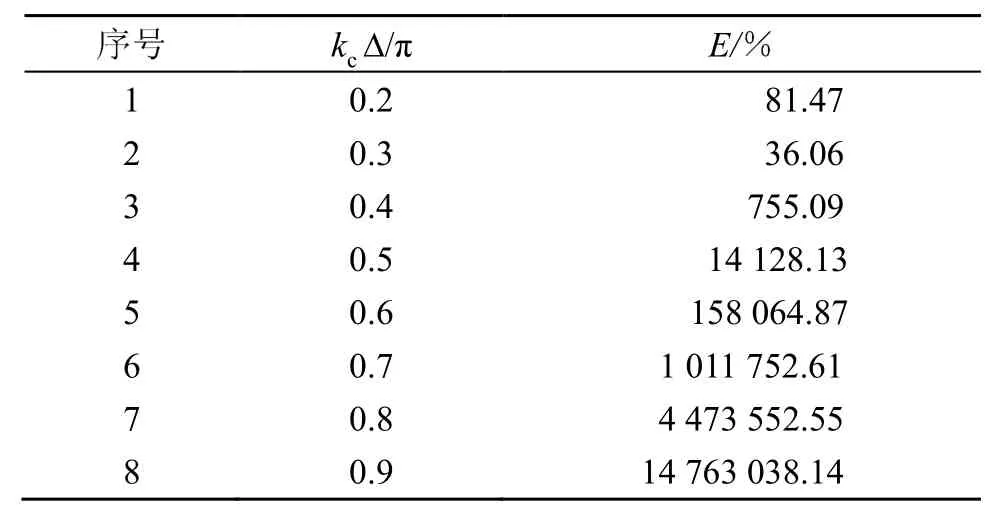
表2 α=0.15时，kc∆/π与E对应关系Table 2 The correspondence between kc∆/π and E,when α=0.15

α值为0.18时，分别取 kcΔ /π的值为0.2、0.3、0.4、0.5、0.6、0.7、0.8、0.9，对相应的反演声源面声压分布效果对比分析如表3所示。

表3 α=0.18时，kc∆/π与E对应关系Table 3 The correspondence between kc∆/π and E,when α=0.18

从表 1、表 2和表 3中不难发现，当α值为0.12、0.15、0.18时，改变kcΔ/π的值，三种情况下均是当 kcΔ/π的值为0.3时，反演效果相对较好。

3.2.2 窗函数陡度系数设计分析

当kcΔ/π的值为0.3时，分别取α值为0.02、0.04、0.06、0.08、0.1、0.12、0.14、0.16、0.18、0.2，对相应的反演声源面声压分布效果对比分析如表4所示。

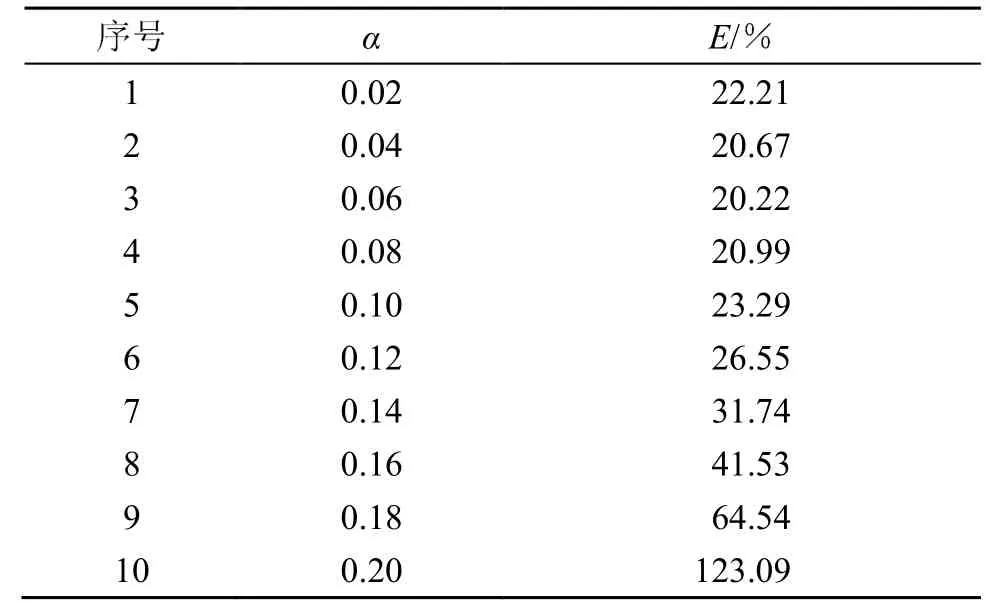
表4 kc∆/π=0.3时，α与E对应关系Table 4 The correspondence between α and E,when kc∆/π=0.3

kc/Δπ的值为0.2时，分别取α值为0.02、0.04、0.06、0.08、0.1、0.12、0.14、0.16、0.18、0.2、0.25、0.3、0.35，如表5所示，对相应的反演声源面声压分布效果进行对比分析。

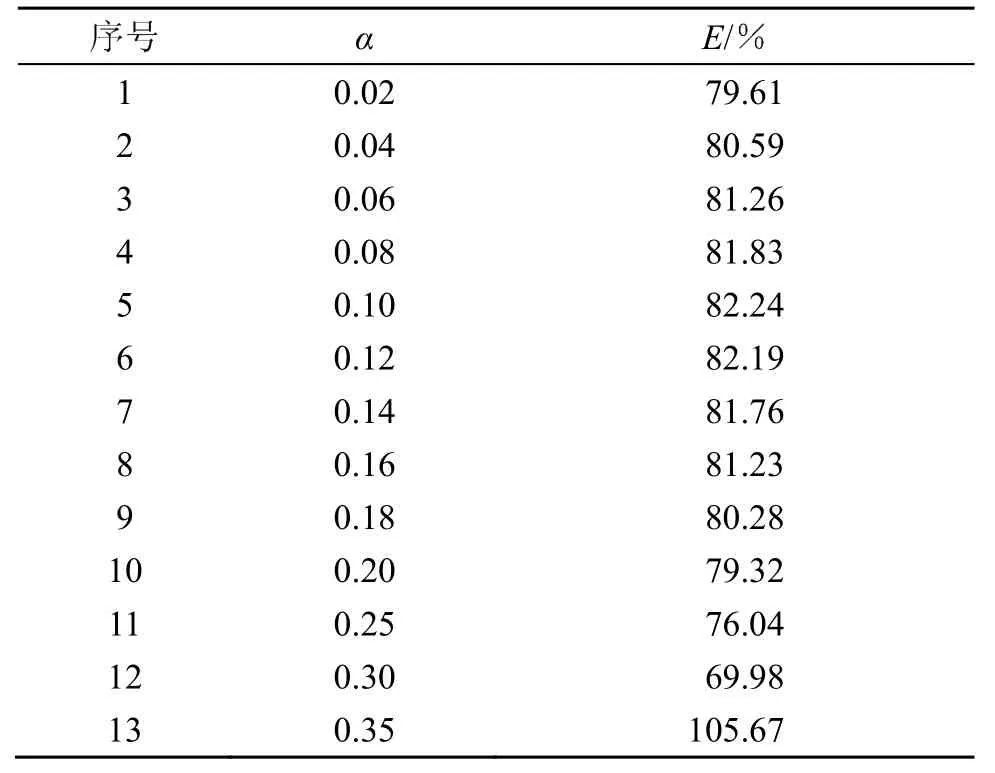
表5 kc∆/π=0.2时，α与E对应关系Table 5 The of correspondence between α and E,when kc∆/π=0.2

kc/Δπ的值为0.4时，分别取α值为0.02、0.04、0.06、0.08、0.1、0.12、0.14、0.16、0.18、0.2，对相应的反演声源面声压分布效果对比分析如表6所示。

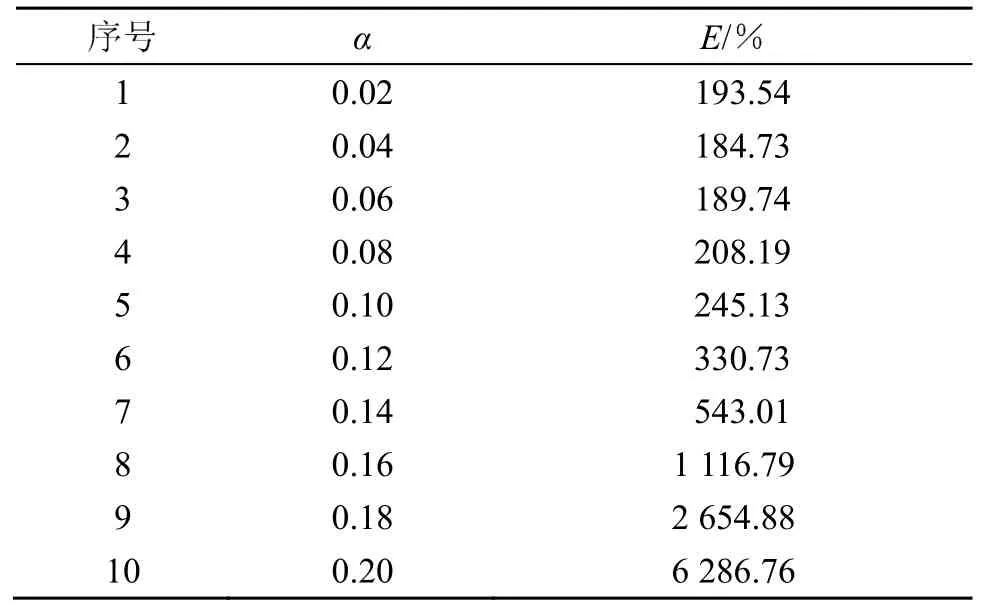
表6 kc∆/π=0.4时，α与E对应关系Table 6 The of correspondence between α and E,when kc∆/π=0.4

通常情况下α的取值范围为0.1～0.2，表4和表6中在对应分析条件下，当α的取值在0.02～0.2中已找到最优取值，而在表5中，α取到了0.35，当α=0.3时E出现最小值，这一结果说明针对不同的全息面参数设计、测量环境以及不同的声源频率，指数滤波器窗函数陡度系数的最优取值并不局限于0.1～0.2。

从表1～6中数据不难看出，kcΔ/π的值为0.3、α的值为0.06时，反演效果最好。且通过对比可以看出，相比较窗函数陡度系数α的取值变化，滤波器截止波数kc的取值变化对反演效果影响更加明显。

3.3 指数滤波器参数设计与声源频率对应关系分析

通过进一步仿真分析，可得到在相同点声源面模型和全息面模型中，对应不同的声源频率时，要取得最优重建效果，相对应的滤波器窗函数陡度系数α和滤波器截止波数kc取值如表7所示。

表7 对应不同声源频率时kc∆/π值，α与E对应关系Table 7 The correspondence of kc∆/π,α and E for the sound sources of different frequencies

从表 7中数据可以看出，声源频率在 100～1 500 Hz之间时，随着声源频率的增加，指数滤波器窗函数的陡度系数α的最优设置逐渐减小，滤波器截止波数kc的最优设置逐渐增大。

4 结 论

本文对平面近场声全息中指数滤波器窗函数设计进行了分析和优化，建立了频率为1 kHz、声源半径为0.01 m和间距为1.5 m的两个模拟点声源模型，以及规模为50 m×50 m、测量间隔分别为50 m、255 m和与声源中心面距离为1 m的全息测量面仿真模型。同时以均匀分布噪声模拟环境噪声。通过分析滤波器截止波数kc和滤波器窗函数陡度系数α的取值对反演误差的影响，找出了kcΔ/π的值为0.3、α的值为0.06时，采用指数滤波器滤波后的反演效果最好。相比较窗函数陡度系数α的取值变化，滤波器截止波数kc的取值变化对反演效果影响更加明显。同时发现，声源频率在100～1 500 Hz之间时，随着声源频率的增加，指数滤波器窗函数的陡度系数α的最优设置逐渐减小，滤波器截止波数kc的最优设置逐渐增大。总结了声源频率在100～1 500 Hz之间时，对应不同声源频率，要取得最优重建效果，滤波器窗函数陡度系数α和滤波器截止波数kc的最优取值，对平面近场声全息中指数滤波器窗函数的设计优化具有重要意义。