一种基于阵列不变量的浅海声源深度分类方法
2021-11-08于喜凤徐哲臻杨坤德
于喜凤,李 辉,3,徐哲臻,杨坤德
(1.西北工业大学航海学院,陕西 西安 710072;2.西北工业大学海洋声学信息感知工业和信息化部重点实验室,陕西 西安 710072;3.国家卫星海洋应用中心,北京 100081)
0 引 言
水下声源深度分类是水声学的重点和难点问题之一。波导不变量是描述浅海声场特性的重要物理量[1]。Turgut等[2]通过实验验证了负跃层环境下波导不变量β的深度特性。宋文华等[3]在浅海负跃层环境中,进行了典型负跃层波导下波导不变量取值的概率分布研究。研究结果表明,在浅海波导中,波导不变量、干涉条纹斜率、声源径向运动速度和距离等物理量之间存在一定的关系。
在声源距离和径向速度已知的情况下,可以从干涉条纹中提取波导不变量[4-5],根据波导不变量的值可以实现水面水下声源分类。刘志韬等[6]提出了一种基于波导不变量的声源深度判别方法,当水听器位于负跃层以下时,根据近水面声源和水下声源的波导不变量数值大小不同进行声源深度判别,但是该方法有一定局限性,即要求声源相对于水听器近似匀速运动。
Lee等[7]提出了阵列不变量的概念用于估计声源距离,该方法不需要环境先验参数信息,计算量很小,而且能充分利用阵列增益。Song等[8]从波导不变量理论出发,将阵列不变量扩展到了波导不变量值不为1的情况,并将其应用于浅海声源定位[9]。针对浅海负跃层环境下声源深度分类问题,本文提出一种在水平不变波导条件下,基于阵列不变量的水面水下声源深度分类的方法:首先在声源距离已知时,利用垂直线列阵来估计阵列不变量,然后利用阵列不变量估计波导不变量β,最后根据β与声源深度的关系,判断声源深度。所提方法在具体环境信息和声源波形未知的情况下依然可行,且计算量较小。计算机仿真表明,在声源距离已知时,所提方法可以实现水面水下声源分类。
1 方法原理
1.1 利用阵列不变量估计波导不变量
阵列不变量根据接收阵列的不同,可以分为水平阵列不变量χh和垂直阵列不变量χv。接收阵列为垂直阵列时,阵列不变量χv被定义为垂直到达角θ的余弦对传播时间t的导数[8],令s=sinθ,可以得到χv的表达式[9]:
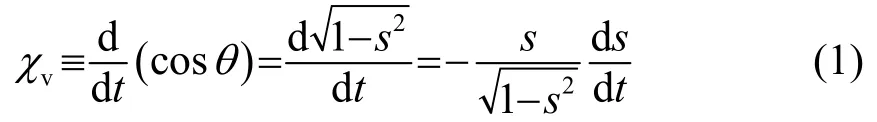
式(1)中,对s、t进行积分可以得到χv与s、t的关系式:

其中:t0、s0分别为任意初始的传播时间和到达角度。式(2)是角度-时间域内的椭圆方程,根据式(2)可以得到阵列不变量χv。
由于海洋波导的物理约束,声波的相位和能量的传播速度不再和介质速度相等。相速度(Vp)是振动状态在介质中的传播速度,群速度(Vg)是能量的传播速度,即信号传播的速度。波导不变量β可由群慢度Sg(群速度Vg的倒数)和相慢度Sp(相速度Vp的倒数)之间的关系来定义:
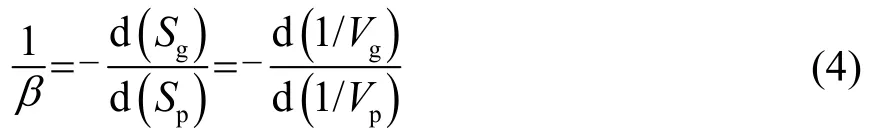
式(4)中群速度可通过计算声源距离R与传播时间t的比值得到,相速度Vp可由接收阵列处的声速c与到达角θ的余弦的比值得到[8]:
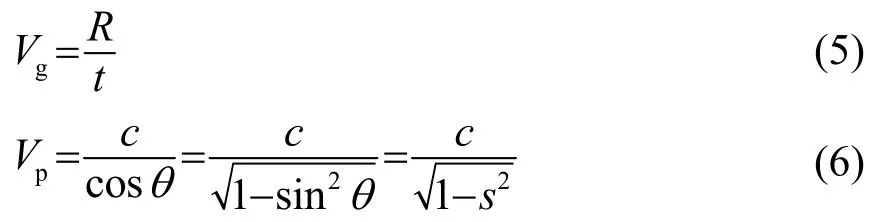
将式(5)和式(6)代入式(4)得到式(7):
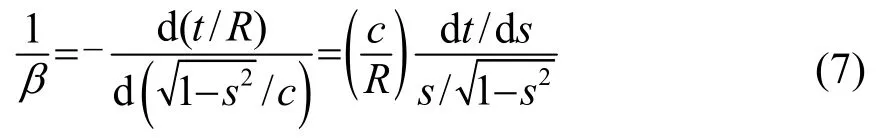
将式(7)代入式(1),可以得到波导不变量β与垂直阵列不变量vχ的线性表达式为

假设波导不变量β值是常数,那么当声源距离已知时,垂直阵列不变量χv也为常数,可以从阵列不变量与波导不变量的线性关系中推导出波导不变量β值。
1.2 波导不变量深度依赖性的理论解释
波导不变量可以由r-ω平面内干涉条纹的斜率表示。Brekhovskikh等[1]将波导不变量β定义为

对于浅海等声速波导,β≈1;对于声速随水深正梯度变化的浅海波导,β为-3。波导不变量具体取值受声速剖面类型、声源信号频率、发射与接收深度等因素影响[10],其中声源深度会显著改变波导不变量β的取值范围[2]。
第m、n号简正波的相慢度差与群慢度差之比可以得到波导不变量分量:

其中:Sp,m、Sg,m分别对应第m号简正波的相慢度和群慢度。波导不变量β可表示为
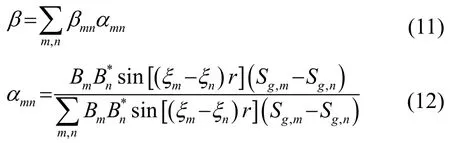
式中:ξm、ξn为第m、n号简正波本征值;Bm、Bn为第m、n号简正波的幅度。由式(11)、(12)可知,声场干涉条纹对应的波导不变量β可表示为各简正波相干项的波导不变量βmn的加权和,权系数αmn反映了第m、n号简正波相干项能量的大小。水平均匀波导中,虽然声源和水听器深度本身不影响简正波的频散特性变化,即βmn不变化,但却能显著改变接收声场中简正波贡献的大小,即αmn的大小,并最终影响到β的最大概率取值[3]。
负跃层环境条件下,声源位于跃层之上时,很难激发出低号的折射类简正波,接收声场主要是由高号的反射类简正波组成;若声源位于跃层之下,声场主要由低号的折射类简正波构成[6]。据此原理,在浅海负跃层环境中,可以通过判断波导不变量值大小实现声源深度分类。
2 计算机仿真
2.1 利用垂直阵估计阵列不变量值
本节进行声源深度分类的仿真研究,以验证该算法的正确性和可行性。仿真环境模型如图1所示,海深100 m,声速剖面是典型的负跃层,跃层深度为10~30 m,其声速从1 520 m·s-1减小到1 480 m·s-1;海底采用半无限空间模型,海底声速为1 580 m·s-1,海底密度为 1.85 g·cm-3,海底吸收系数为0.04 dB·λ-1;声源频率为350 Hz,距离为5.5 km。接收阵列由16个阵元组成,其中1#阵元深度为45 m,16#阵元深度为70 m,阵元垂直等间距分布。当声源频率与海水声速 c、海水深度H满足f>10c/H时,可以利用Bellhop模型进行声场计算。
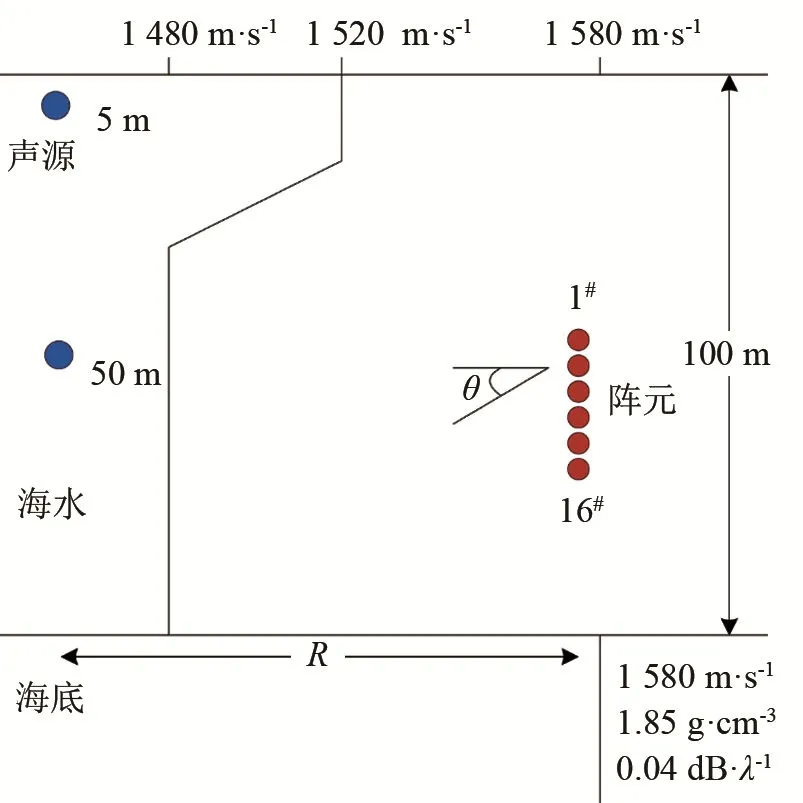
图1 仿真环境模型Fig.1 Model of simulated environment
根据阵列不变量理论,传播时间t与垂直到达角度θ之间存在约束关系,利用Bellhop模型仿真得到的到达时延与到达角的计算值,其分布服从式(2)所示角度-时间域内的椭圆方程;对计算值进行曲线拟合后得到波束时间迁移线,垂直阵列不变量为拟合椭圆半长轴的负倒数。声源深度分别为5 m和50 m时,波束时间迁移图如图2和图3所示。
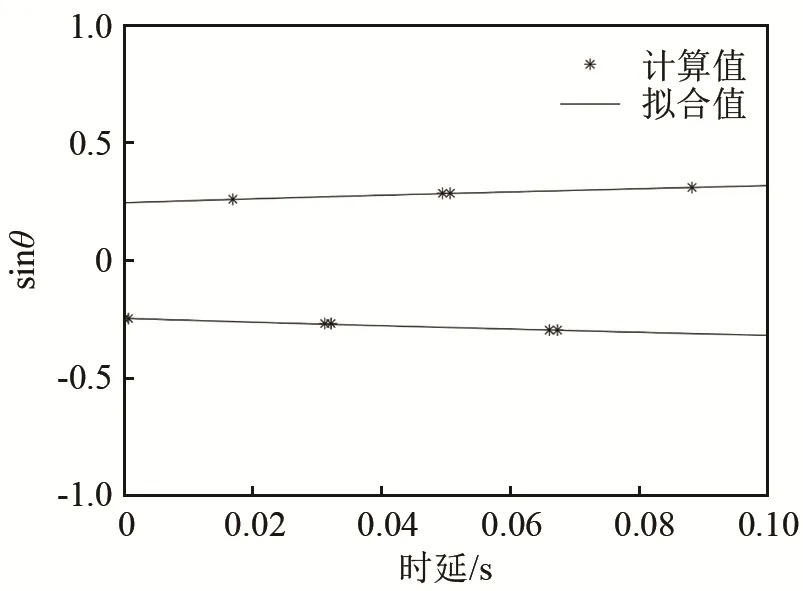
图2 声源深度5 m时的波束时间迁移图Fig.2 Beam-time migration of the sound source at depth of 5 m
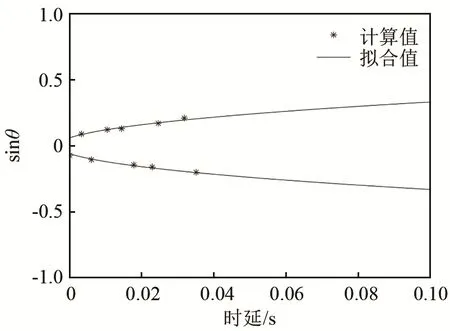
图3 声源深度50 m时的波束时间迁移图Fig.3 Beam-time migration of the sound source at depth of 50 m
根据曲线拟合得到声源深度为5 m和50 m时对应的阵列不变量χv的值分别为-0.217和-0.545。因为声源距离已知,根据式(8)即可推导出波导不变量值。当声源深度为5 m时,β小于1,具体值为0.776;当声源深度为50 m时,β大于1,具体值为1.999。
2.2 波导不变量随声源深度的变化关系
为了验证用阵列不变量进行水面水下声源分类的可行性,本节对从声场干涉条纹中提取的波导不变量值与从阵列不变量中提取的波导不变量值进行对比,并给出水面水下声源分类的判别标准。
环境模型如图 1所示,声场计算采用 Bellhop模型,计算的频带范围是 200~500 Hz,水平接收距离为5~6 km,接收水听器深度为50 m,图4和图5分别给出了声源深度为5 m和50 m时的声场干涉结果,在空频(距离-频率)域内声压呈现出亮暗相间的干涉条纹。
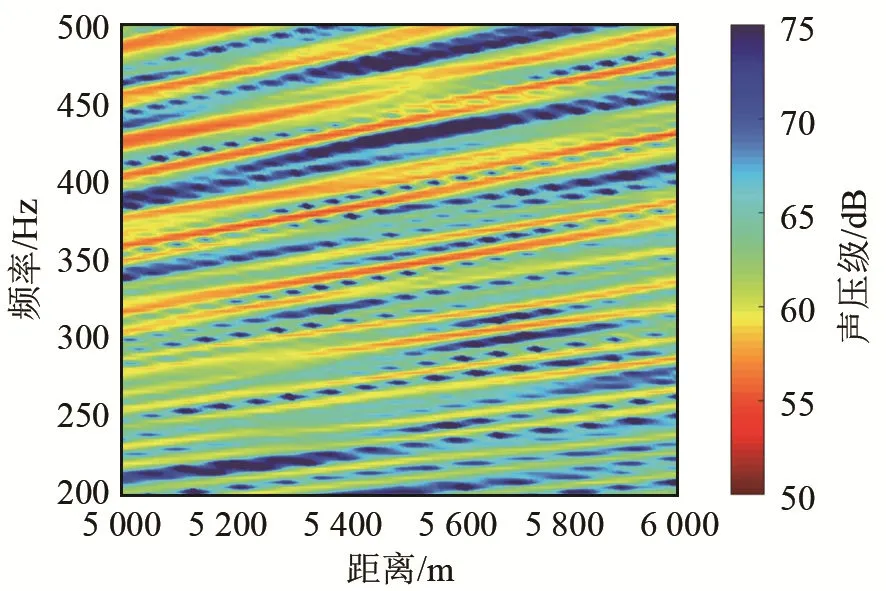
图4 声源深度5 m时的声场干涉图Fig.4 The sound field interferogram of the sound source at depth of 5 m
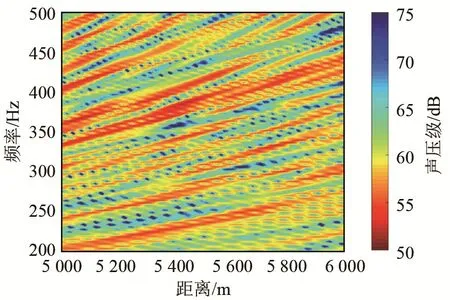
图5 声源深度50 m时声场干涉图Fig.5 The sound field interferogram of the sound source at depth of 50 m
从图4和图5中可以看出,声源深度不同时,干涉条纹的精细结构和斜率也不完全相同。负跃层声速剖面情况下,声场的干涉条纹结构复杂,条纹斜率以及相应的波导不变量取值具有一定的分布范围。使用二维傅里叶变换方法提取波导不变量[11],β的相对概率分布情况如图6和图7所示。可以看出,当声源位于负跃层以上时,波导不变量分布的峰值位置在0.8左右;声源位于负跃层以下时,波导不变量分布的峰值位置明显大于1,主要分布在1.3~1.7内。上述结果与利用阵列不变量求取的波导不变量一致。
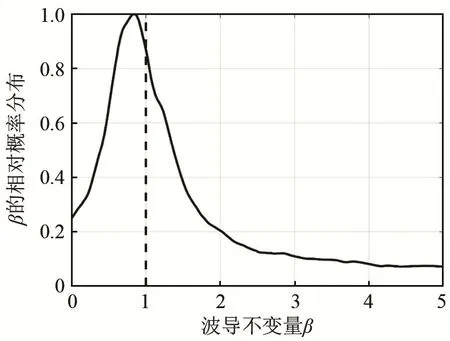
图6 声源深度为5 m时的波导不变量分布Fig.6 Waveguide invariant distribution of the sound source at depth of 5 m
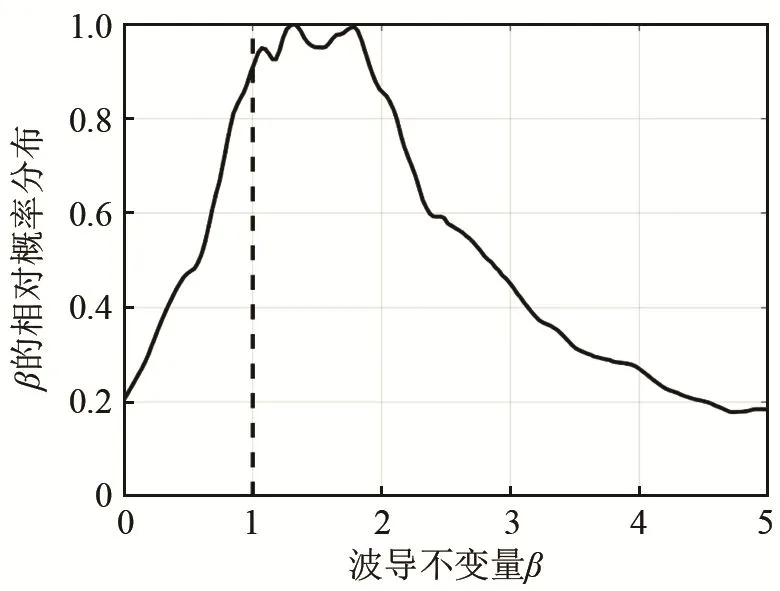
图7 声源深度为50 m时的波导不变量分布Fig.7 Waveguide invariant distribution of the sound source at depth of 50 m
利用式(8)得到的波导不变量β随声源深度的变化情况如图8所示,图中虚线为等声速环境下波导不变量值随声源深度的变化情况,实线为负跃层环境下波导不变量值随声源深度的变化情况。
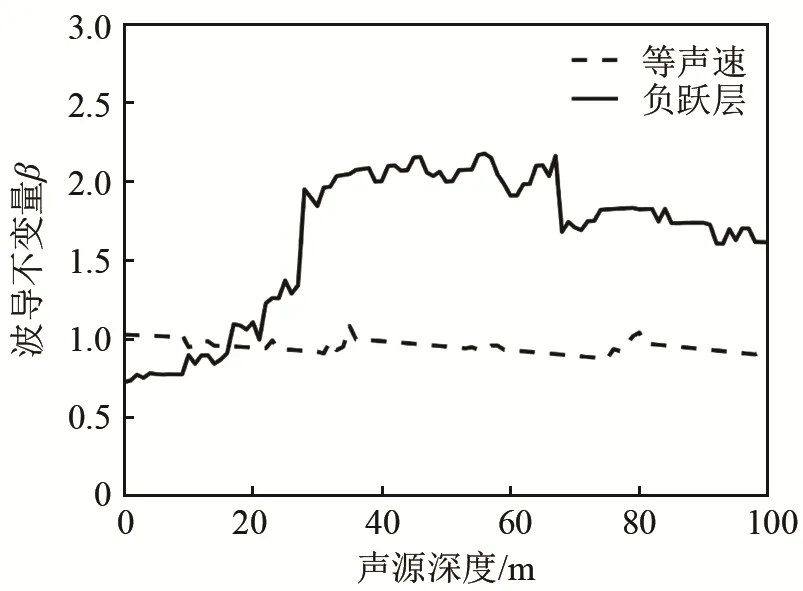
图8 波导不变量在不同声源深度时的变化情况Fig.8 Waveguide invariants of the sound source at different depths
从图8可以看出,等声速环境条件下,波导不变量β≈1;负跃层环境条件下,波导不变量随声源深度产生了显著变化,近水面声源与水下声源的波导不变量差别明显。当水听器位于负跃层以下,声源位于负跃层以上时,波导不变量小于 1,而当声源位于负跃层以下时,波导不变量大于1。所以,利用阵列不变量进行负跃层以上的水面声源和负跃层以下的水下声源深度分类是可行的。
2.3 阵列不变量判别深度方法的性能研究
2.3.1 接收深度的影响
前文利用Bellhop模型的接收深度是50 m,在浅海负跃层条件下可以依据阵列不变量估计的波导不变量的差异分辨出近水面声源和水下声源,接下来讨论接收深度对声源深度分类的影响,仿真条件如图1,负跃层深度在10~30 m之间,5 m处声源与50 m处声源波导不变量值随接收深度的变化情况如图9所示。
从图9中可以看到,当接收深度位于负跃层以上时,水面水下声源的波导不变量均小于 1,差别不大,难以分辨声源深度;但当接收深度位于负跃层以下时,水下声源的波导不变量值与近水面声源相比差异明显,在这种情况下可以实现声源深度的分类。
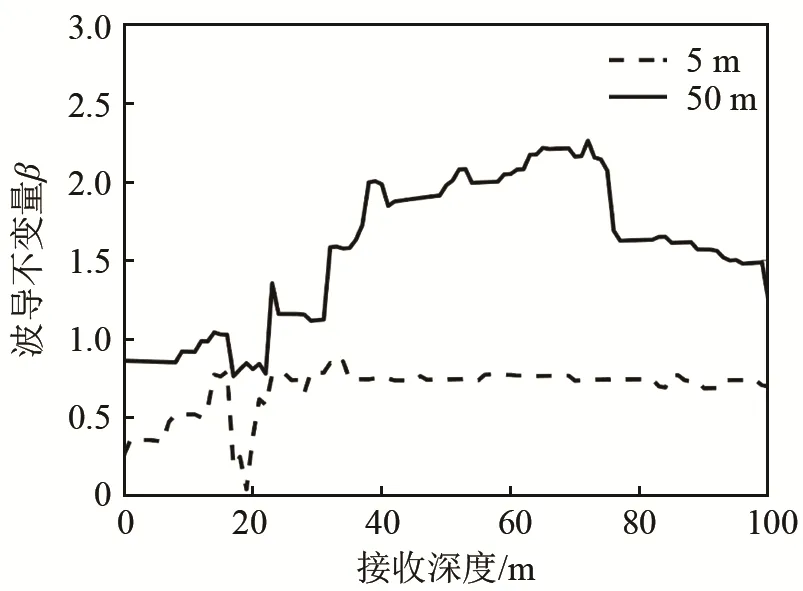
图9 波导不变量在不同接收深度时的变化情况Fig.9 Waveguide invariants of the receiver at different depths
2.3.2 声源距离的影响
讨论声源距离对分辨近水面声源和水下声源的影响,声源深度和负跃层声速剖面条件参数同图1。5 m处声源与50 m处声源波导不变量随声源距离的变化情况如图10所示。
从图10中可以看到,近水面声源波导不变量小于 1,水下声源的波导不变量值大于 1,波导不变量在不同声源距离下没有明显变化,声源距离的变化对该方法影响较小。
2.3.3 负跃层厚度、波导水深变化的影响
本节讨论负跃层厚度和波导深度对该方法性能的影响,仿真条件如图1。波导水深100 m,负跃层深度在10~20m、10~30 m、10~40 m之间时,波导不变量随声源深度变化情况如图11所示。从图11中可以看出,水面水下声源波导不变量差值会因负跃层厚度的变化而变化,但对判别声源位于跃变层以上还是以下的结果影响不大。
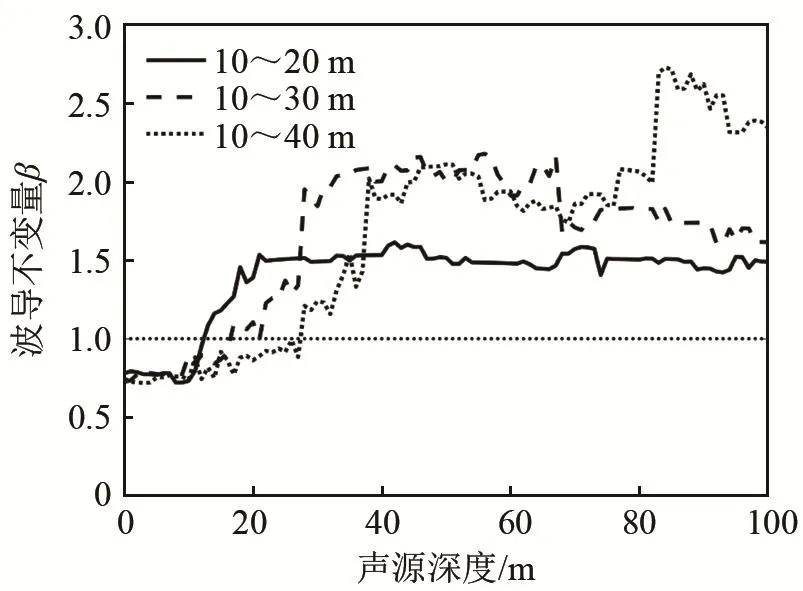
图11 不同负跃层厚度时波导不变量的变化情况Fig.11 Waveguide invariants for different thermocline thicknesses
负跃层深度在10~30 m之间,阵中心位于海底之上30 m,波导深度为70、130 m时波导不变量值随声源深度变化情况分别如图 12、13所示。从图12、13中可以看出,当负跃层厚度、深度、强度不变,但海深变化时,水面水下声源的波导不变量差值会因波导深度的增大而减小,但依然可以通过波导不变量判断声源深度是在跃变层以上还是跃变层以下。
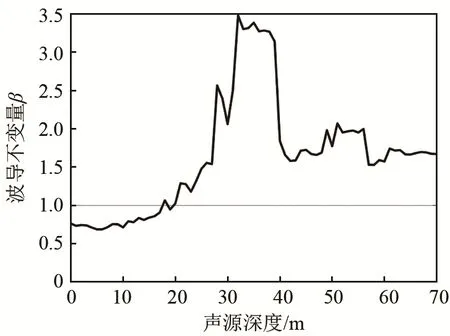
图12 海深70 m时波导不变量的变化情况Fig.12 Waveguide invarian at a sea depth of 70 m
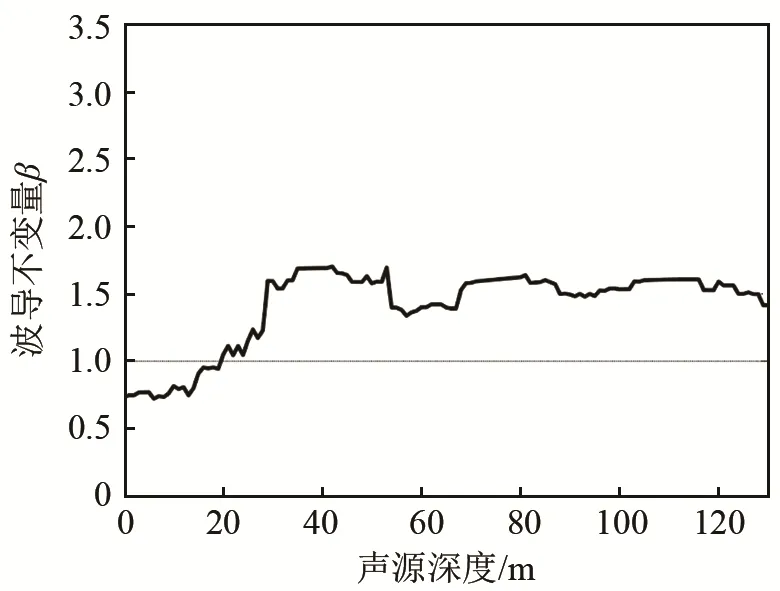
图13 海深130 m时波导不变量的变化情况Fig.13 Waveguide invariant at a sea depth of 130 m
此外,因为本文所提方法涉及波束形成方位估计,因此,阵列孔径越大,方位估计角度分辨率越高,阵列不变量值估计结果就越准确。
3 结 论
本文利用阵列不变量与波导不变量之间的线性关系,提出了一种基于阵列不变量的声源深度分类方法,可适用于浅海负跃层环境。在具体环境信息和声源波形未知的情况下,针对距离已知且相对于接收阵无径向距离变化的声源,通过垂直阵的阵列不变量值估计波导不变量的数值,进而根据波导不变量的声源深度依赖性实现声源深度判别。计算机仿真结果表明,在浅海负跃层环境中,使用阵列不变量值估计出的波导不变量与传统基于干涉条纹斜率估计出的波导不变量一致,可以用于实现水面水下声源的深度分类。
