交叉层波束形成方法的发动机噪声源识别

张 智，邓建交，刘英杰，李凌志，安孝文，胡宇宁

（1.汽车振动噪声与安全控制综合技术国家重点实验室，吉林 长春 130011；2.中国第一汽车股份有限公司研发总院NVH研究所，吉林 长春 130011；3.中国第一汽车股份有限公司解放事业部商用车开发院，吉林 长春 130011）

0 引 言

发动机是车辆最主要的噪声源之一，尤其在汽车怠速、加速工况下，发动机噪声成为整车噪声最大的来源，因此设法降低发动机噪声，是优化整车噪声水平的重要途径。由于发动机具有体积大、附件多等特点，且噪声源通常分布在发动机的各个表面上，常规的测试方法不易准确判断，为发动机噪声控制带来了一定的难度。对于整车状态的发动机噪声源定位测试，由于发动机舱内环境复杂，反射面多，且发动机侧面被遮挡，仅从发动机上表面或下表面进行识别分析往往得不到理想的结果。因此需要利用发动机台架，结合噪声源识别手段测试分析，准确识别发动机表面的声源分布及特征，从而为进一步的发动机噪声控制优化提供可靠的依据和有针对性的指导。

对发动机进行声源识别的常用方法是声强法、近场声全息与波束形成方法[1-3]。声强法可以准确地测量平面上的声源分布及声功率辐射，但一般只适用于稳态工况且测试耗时极长，测试成本高，多用于特定工况的异响声源排查[4-7]；近场声全息利用阵列接收的声场数据，基于赫姆霍兹积分方程和三维空间傅里叶变换，可准确重构三维声场的声压、质点速度和声强，从而得到发动机表面的声源分布，但其测试距离一般要求小于 0.1 m，对于发动机的试验室台架测试，由于发动机表面附件、管路、线束及进排气管路支架布置的影响，阵列不易靠近发动机表面，使用近场声全息方法测试较为困难，对于普通的阵列尺寸，通常不能完整覆盖发动机单侧表面，需要多次测试后进行拼接，测试效率低，成本高，且近场声全息主要应用于低频噪声源识别[8]。波束形成方法通过对阵列传声器接收到的声压信号的处理，即根据声源计算平面的聚焦网格点与阵列传声器测点的空间矢量关系，将各通道信号进行相位对齐并求和，从而得到被测平面的声源分布，可对超出阵列尺寸外的位置进行声源识别，即发动机的每个面，仅需一次测量就可得到完整的识别结果，具有测量速度快，中高频分辨率好，可中远距离测量的优势[9-15]，对于本文所测试的发动机尺寸，使用波束形成方法的测试时间仅为声全息方法的四分之一，为声强法的数十分之一，且对3 kHz以上的高频噪声具有更高的识别精度。

本文使用波束形成方法对发动机的上、前、左、右四个面进行声源识别测试，避免主要声源出现在波束形成面之外，并通过交叉层法计算得到声源的三维分布结果。以往的波束形成法进行噪声源识别，通常只对较大的平面或声源可能分布的平面进行测试。对于声源分布复杂的被测对象，往往得不到理想的识别结果[16]，主要原因一是有较主要的声源未处于波束形成面，识别结果虽然显示出了该声源在波束形成面上的投影，但该投影并非垂直于波束形成面，而是沿波束方向在波束形成面上的投影，如图1所示；原因二是位于非被测表面的声源由于被测对象的遮挡，存在明显的衍射，破坏了直达声场条件，导致其到某些阵元的声程发生改变，即相位发生偏移而无法在真实位置形成声源图像；原因三是远离波束形成面的声源在计算时，由于其能量在波束形成面不聚焦，会明显低于其真实值，导致其被其他主要声源的旁瓣掩盖，或未达到识别动态范围而导致遗漏[17]。

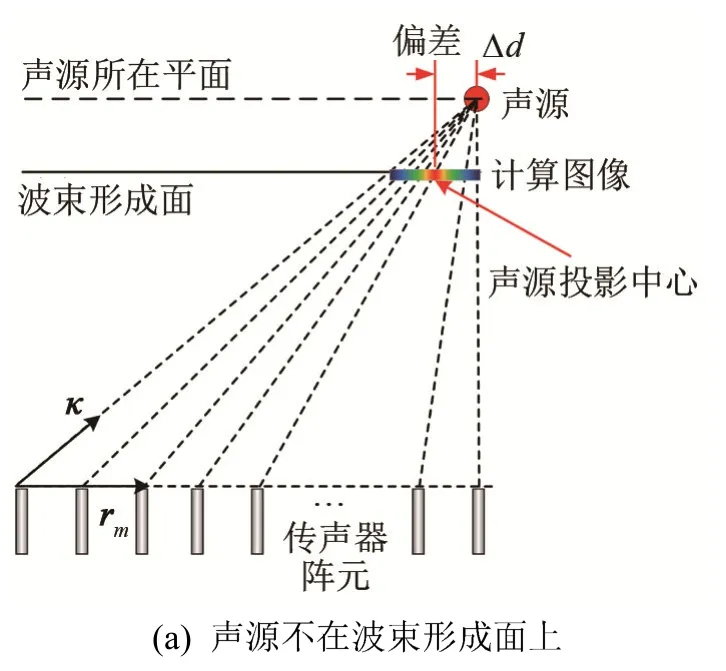
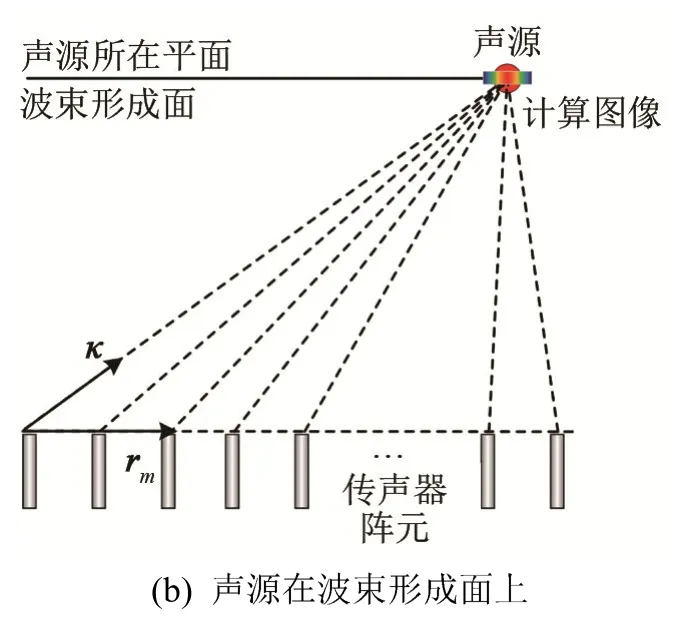
图1 声源与波束形成面相对位置对计算结果影响Fig.1 The influence of the relative position between sound source and beamforming surface on the calculation results

1 波束形成理论及算法

1.1 波束形成理论

采用一组在空间固定位置上分布的传声器组成的阵列对空间声场进行测量，通过对每个固定位置上的传声器测得的声压信号进行特殊的处理，就可以获得有关声场的声源信息，在信号处理领域，这种对阵列信号的处理算法被称为“波束形成（Beamforming）”，而传声器阵列的聚焦方向称为“波束”（或主波瓣）。该技术同样广泛应用于雷达、声呐、通信等领域[18]。

根据声源计算平面的聚焦网格点与阵列传声器测点的空间矢量关系，对传声器阵列中各通道信号进行延时，即根据各测点的声程差来调整相位差，补偿各阵元测点的传播延时，从而使某一期望方向上的信号到达阵列所有测点都是同相位的，这样，在聚焦方向上产生一个空间响应极大值，达到空间滤波作用[19]。

平面波波束形成示意图如图 2所示。在空间x-y平面内的平面阵列的M个传声器，传声器位置为rm（m=1,2,…,M）,接收来自-κ方向的一列平面波。波束形成的过程是将每个传声器接收的信号相对于参考传声器进行延时，从而使所有传声器对于同一聚焦方向，接收的是同一瞬间波前，然后求和，这样该聚焦方向的信号由于是同相位相加，相当于增强了M倍，而其他方向的信号由于相位差，则会减弱，传声器数量越多，这种增强和减弱的效果也就越明显。

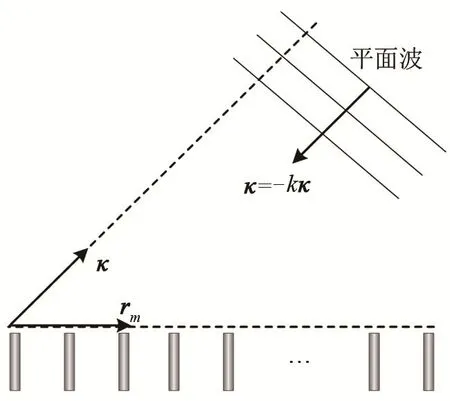
图2 平面波波束形成示意图Fig.2 Schematic diagram of plane wave beamforming

波束形成的输出为

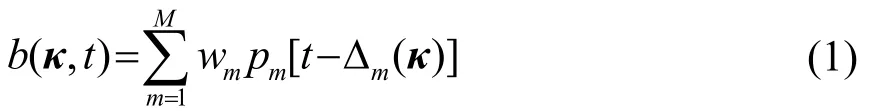
式中，M是传声器的个数，wm是第m个传声器的加权系数，pm（t）是第m个传声器测得的声压信号。Δm（κ）是波束聚焦方向为κ时，第m个传声器相对于参考点的时延。由图2中几何关系有：

式中，κ为聚焦方向矢量，rm是第m个传声器到参考点的相对位置矢量，κ·rm即为rm在κ方向的投影，c为传播介质中的声速。

以上即为延时求和的理论依据。由于时域信号数据量非常大，影响计算效率，实际计算中，采用频域法可显著提升计算速度和节省数据占用空间。使用频域计算波束形成的输出功率为：

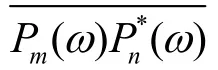
1.2 位于同一平面声源的波束形成仿真验证

使用Matlab软件建立波束形成仿真模型。设置若干仿真声源，声源所在平面平行于阵列所在平面，使用间距0.1 m的8×8通道矩形阵列对声源信号进行接收，如图3（a）所示。假设声源发出稳态单频信号，则阵列阵元接收信号为

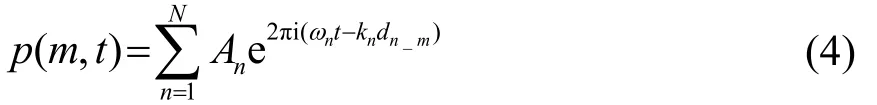
式中，m为阵元序号，t为时间序列，N为仿真声源数量，n为仿真声源序号，ωn为第n个仿真声源的频率，A为声源幅值，k为波数，dn_m为第n个声源与第m个阵元的距离。

根据全部阵元接收到的仿真信号，计算声源所在平面的声源分布，用4个声源作示例，结果如图3（b）所示，全部声源均准确识别。

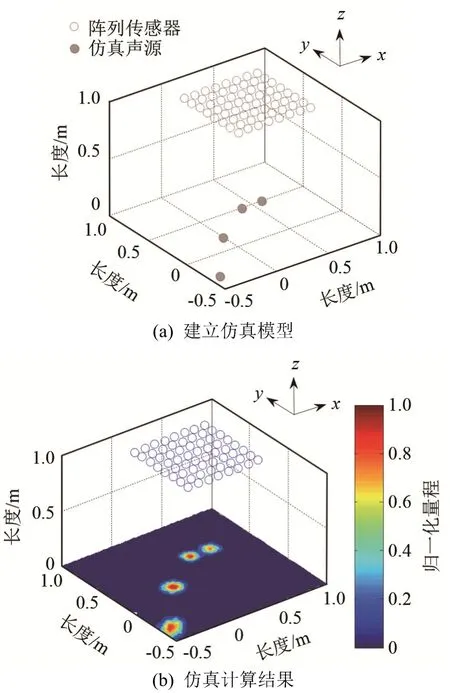
图3 位于同一平面的声源识别仿真计算结果Fig.3 Simulation results of source identification in the same plane

1.3 位于不同平面声源的波束形成仿真验证

对于发动机等被测对象，轮系及各种附件布置复杂，其主要声源往往在各个面上都有分布，而对处于波束形成面之外的声源，往往无法得到有效的判断。尤其是识别图像显示在棱上的结果，在仅测试一个面的情况下，由于无法得到其纵深信息，不能判断真实声源是在棱上，还是在与波束形成面垂直的面上。

设置4个声源分布在一个假想的长方体上，进行仿真，其坐标分别为：

声源1位置ps1=[0.4 0.4 0.32];

声源2位置ps2=[0.4 0.2 0.32];

声源3位置ps3=[0 0.2 0.32];

声源4位置ps4=[0 0.2 0.12]。

如图4所示，声源1位于上面，声源2及声源4位于棱上，声源3位于顶点。

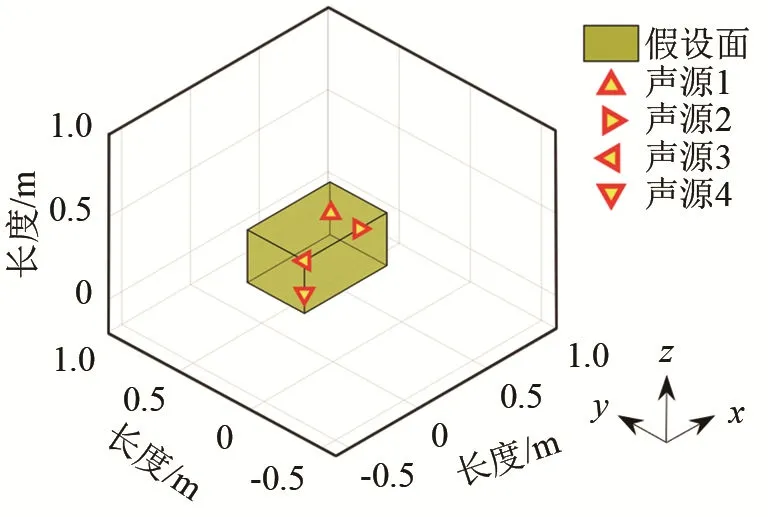
图4 位于不同平面的声源Fig.4 Sound sources in different planes

分别从三个方向对上述位于不同平面的四个声源进行识别，得到的图像结果都只显示出了三个声源，如图5所示。如果仅从一幅图像进行识别，必然导致对声源的位置误判或遗漏。

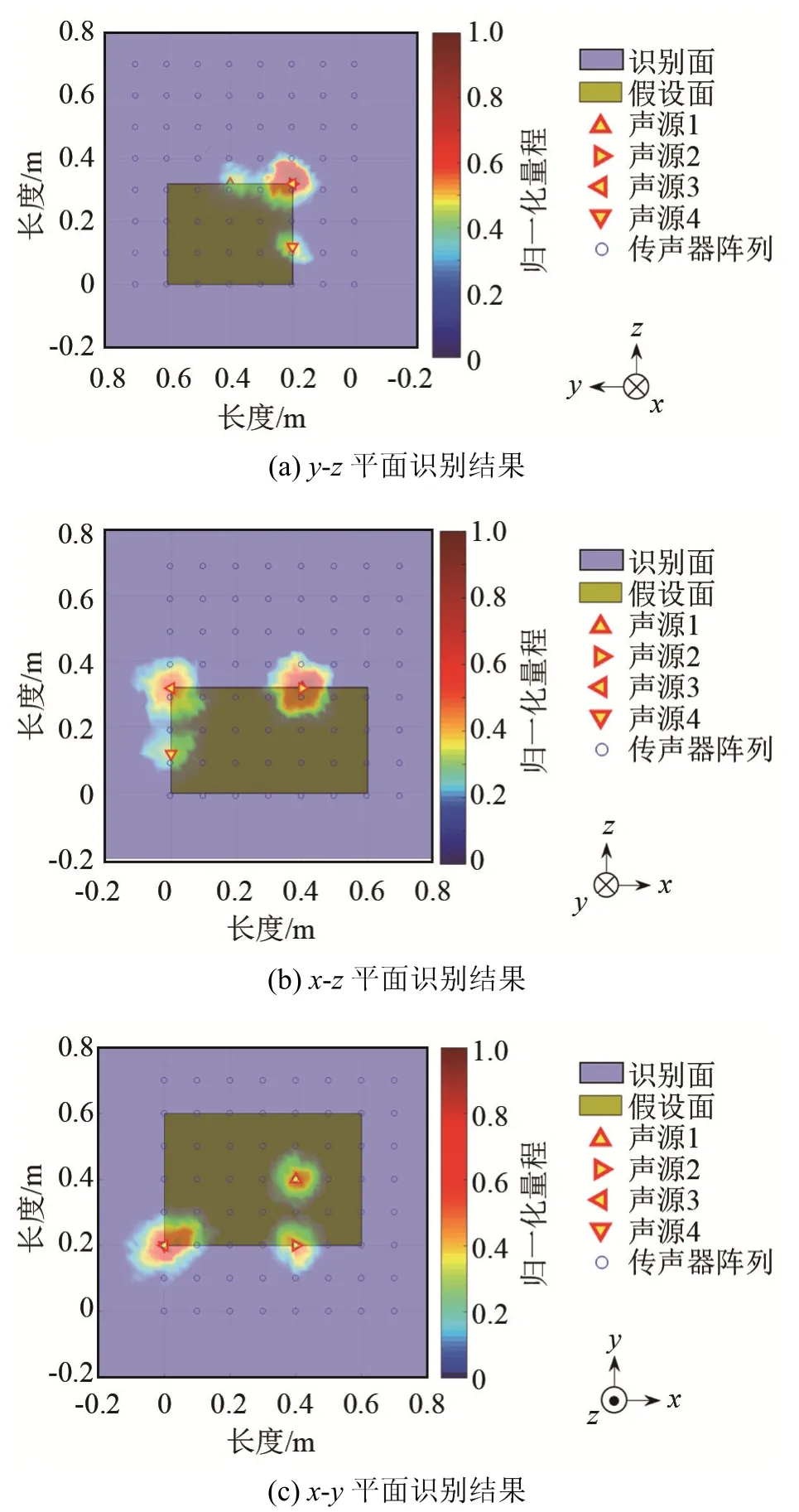
图5 位于不同平面的声源识别仿真（三向投影）Fig.5 Simulation of sound source identification in different planes（axonometric projection）

位于不同平面的声源识别仿真（三维图）如图 6所示。可见，对于不处于波束形成面上的声源，可能得到其真实声源在波束形成面上的投影，如图6（a）中的声源1。而如果在其投影位置恰好有另外一个声源，两者的识别图像将会重合，从而无法分辨出是一个还是多个声源，如图 6（a）中的声源 2、图6（b）中的声源1及图6（c）中的声源4所示。

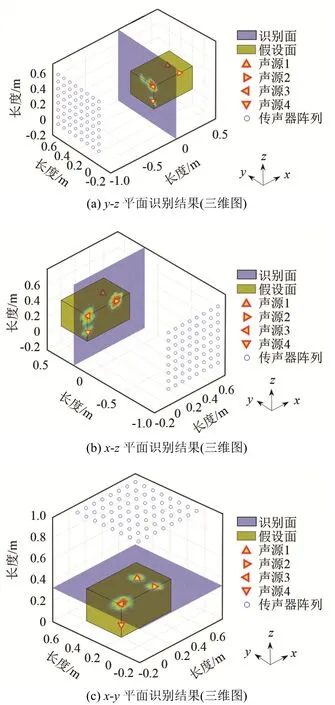
图6 位于不同平面的声源识别仿真（三维图）Fig.6 Simulation of sound source identification in different planes（stereograph）

1.4 多维交叉层法波束形成声源识别仿真

将波束形成平面与阵列平面距离以一定步长改变，计算多个形成面的分布结果，覆盖被识别对象的纵向深度，则可得到一系列平行的形成面，如图7所示。

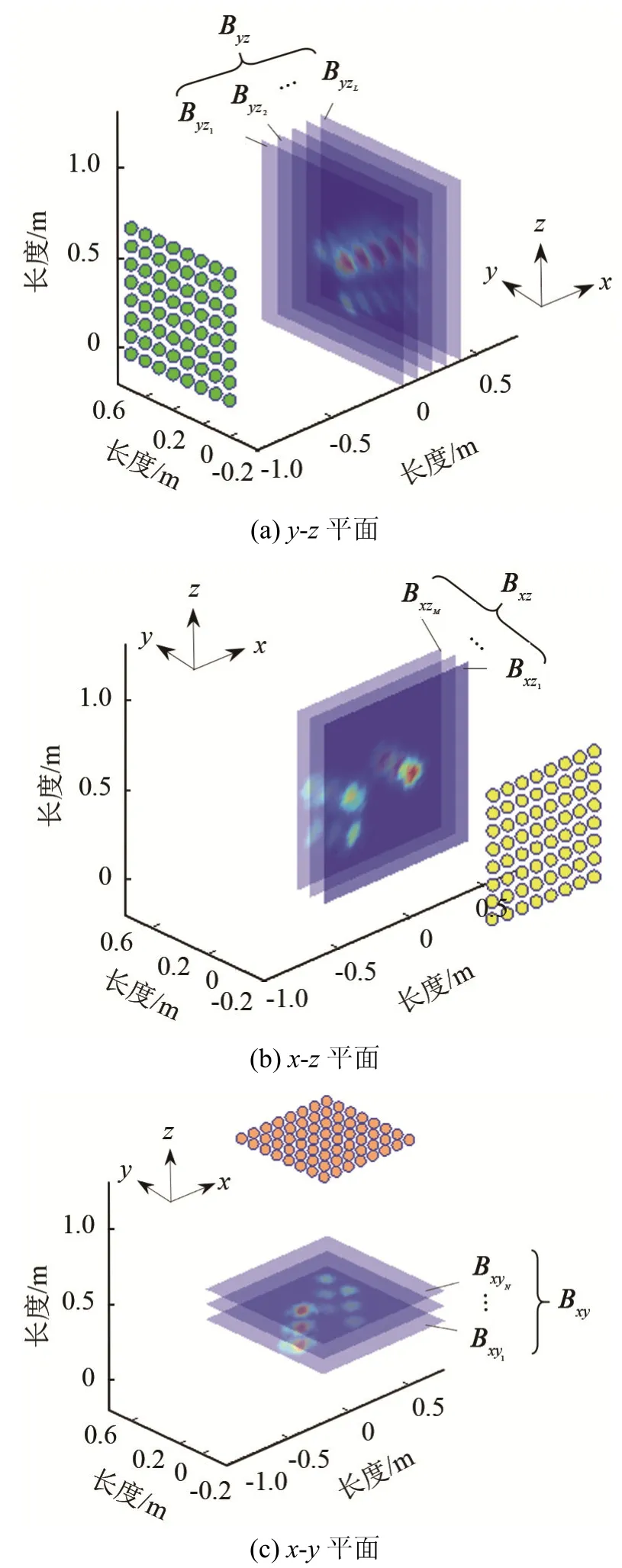
图7 波束形成分层计算Fig.7 Layered computation of beamforming

对y-z平面、z-x平面、x-y平面的计算层数分别为L、M、N层，则y-z平面的第l层的波束形成面结果为

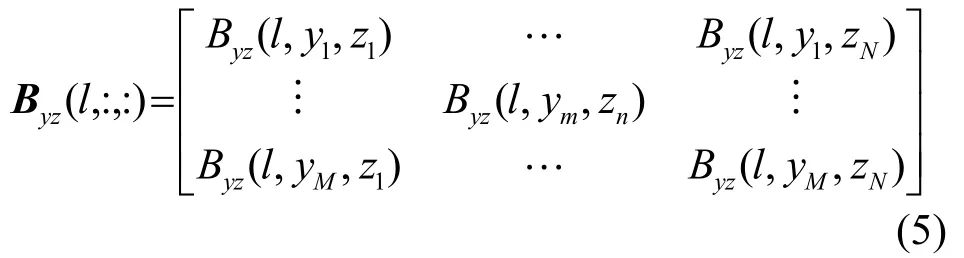
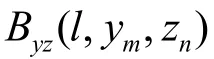
同理：

可对数据进行适当截取，使Byz、Bzx、Bxy的x、y、z坐标对齐。

被测对象所处的几何空间，被正交的三个方向的平面分层切割，该空间内的每个聚焦点皆为三个方向平面的交叉点，即每个聚焦点被三个方向各计算了一次，如图8所示。

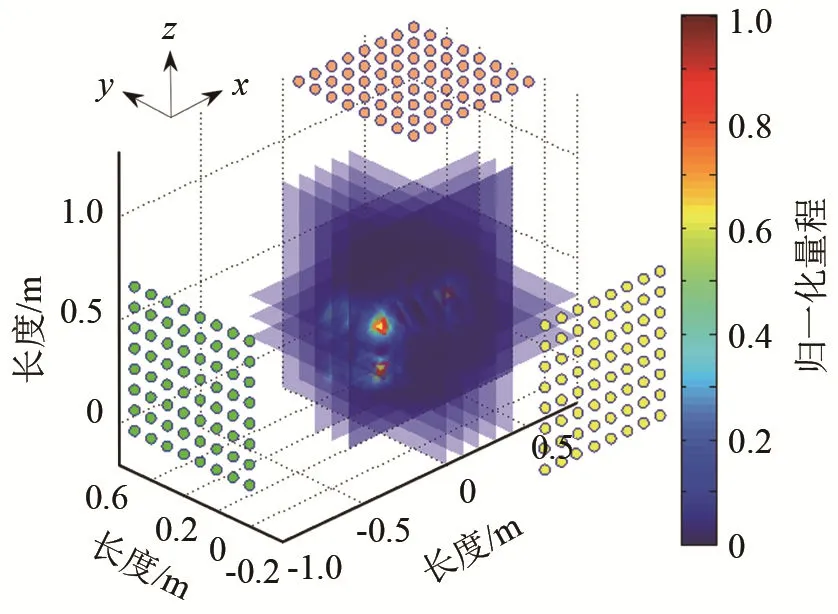
图8 多维交叉层计算过程Fig.8 Calculation process of multi-dimensional cross-layer method

对于虚假的声源投影，仅在其中一或两个方向的识别面上显示，即在其中一或两个三维矩阵中出现大值，在另外的矩阵里则会呈现小值，故将三个三维矩阵的对应点相乘，再开立方恢复幅值，即得到交叉层结果：

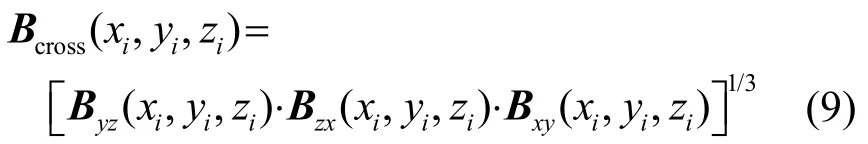
则在结果Bcross中，虚假声源所对应的点受其中的小值因数影响而减小，真实声源所对应的点为三个大因数相乘而不受影响。

由于仅考虑位于物体表面的声源，可去除位于物体内部的点，仅保留构成被测物表面的点进行计算，结果如图9所示。可见，对于分布在不同表面上的各个声源，均得到准确识别。图5（a）及图6（a）中的虚假声源投影在图9中已消除，且可同时显示出各个面的声源分布。

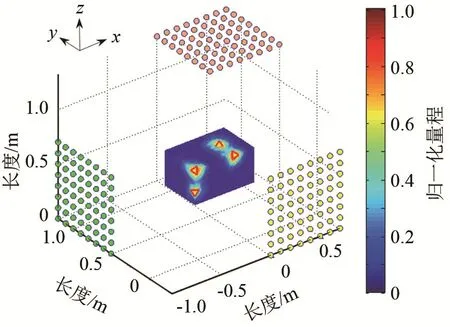
图9 多维交叉层计算结果Fig.9 Calculation result of multi-dimensional cross-layer method

2 发动机声源识别

2.1 阵列布置及现场测试

使用间距为0.1 m的8×8通道矩形阵列对柴油发动机的上、前、左、右四个面分别进行测试。阵列平面平行于发动机被测面，发动机左面的测量现场布置如图 10（a）所示。依据发动机尺寸、阵列尺寸以及两者位置对应关系，计算出阵元在发动机表面的投影位置，如图10（b）所示。声源识别的结果即在此基础上进行显示。

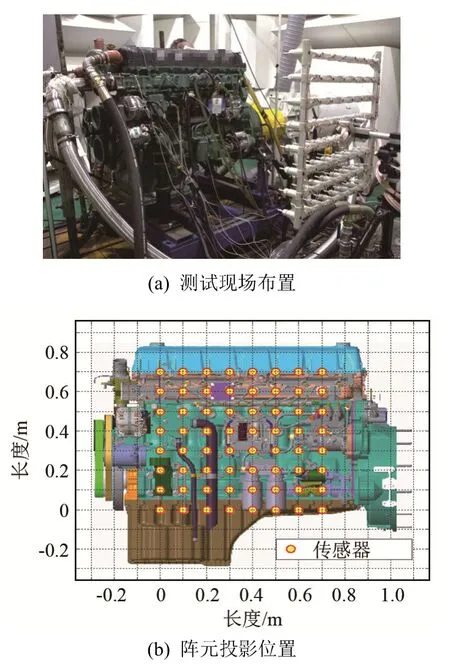
图10 发动机左面测试阵列布置Fig.10 Layout of the test array at the left side of engine

2.2 发动机声源频率特征

通过对发动机进行变转速工况测试，得到发动机噪声声压级的时频结果，如图 11所示。通过观察，可得知发动机的各主要噪声频率及其对应转速。在实际应用中，可选择需要关注的噪声成分进行分析。

2.3 声源平面识别结果

以图 11中所标示的噪声为例，其对应发动机转速为：1 600～1 800 r·min-1，频率范围为：2 800～3 300 Hz。发动机各个面的识别结果如图12所示。

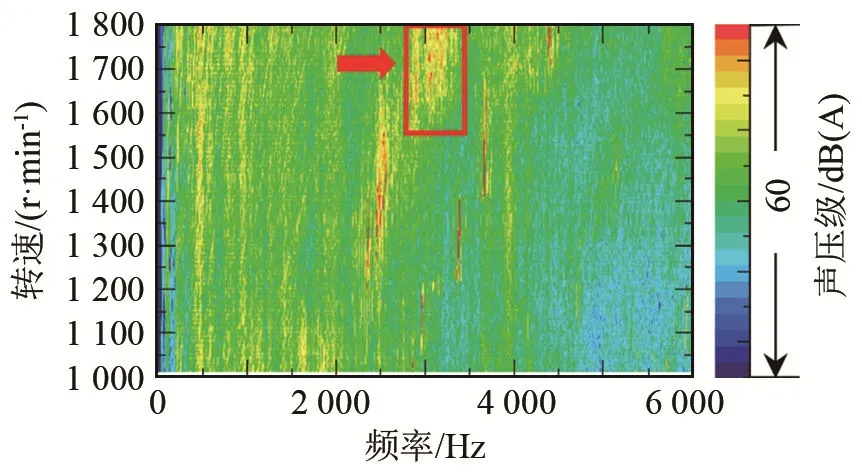
图11 满负荷情况下发动机噪声声压级的转速-频率图（阵列中心测点）Fig.11 Speed-frequency diagram of full-loaded engine noise level measured at the central point of the array

2.4 多维交叉层法计算结果

使用从不同方向的测试数据，通过多维交叉层法进行计算，得到声源在发动机表面的立体分布结果，如图13所示。

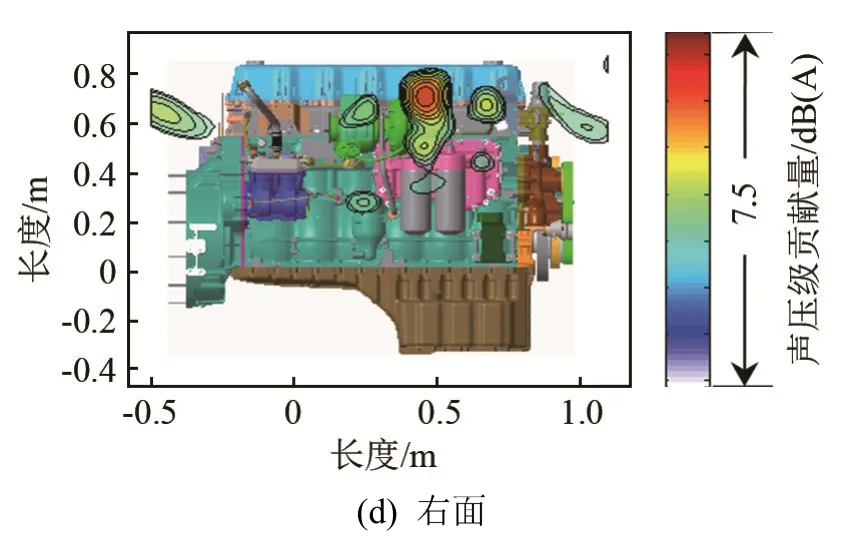
图12 发动机噪声（2 800～3 300 Hz,1 600～1 800 r·min-1）识别结果Fig.12 Identification results of engine noise source at the frequencies of 2 800～3 300 Hz and the speeds of 1 600～1 800 r·min-1

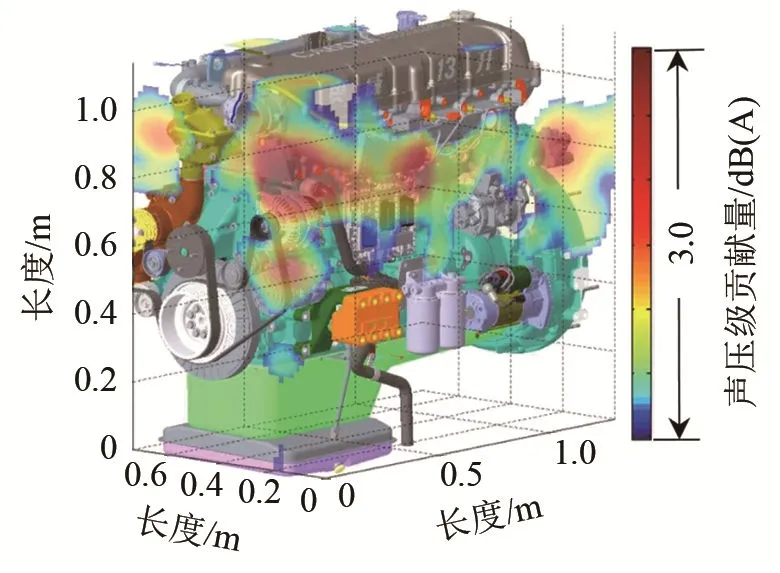
图13 多维交叉层法声源识别结果Fig.13 Identification results of engine noise source by cross-layer method

对于这种声源分布复杂的情况，利用任何一个平面的识别结果，都无法准确进行识别。如图12（a）中的下方显示的多个声源，在图12（c）中，发现这些声源并非位于发动机的棱上，即不在发动机上表面，而是分布在发动机的左面，在对发动机上面进行识别计算时，这些声源投影在了平行于发动机上面的波束形成面上。而利用交叉层法计算得到的立体结果，则直观显示出声源的位置，去除了声源投影的干扰。

对于上述噪声，定位结果分别为前面的进气管口转折处，如图14（a）所示；右面的涡轮增压器管口位置，如图14（b）所示；左面的油泵位置、油轨及起动机附近，如图14（c）所示。

图14 噪声源识别结果与实物对应关系Fig.14 Corresponding relation between the identified engine noise sources and the actual engine parts

3 结 论

本文利用平面传声器阵列对某发动机的各表面进行测试，使用波束形成法对发动机的主要噪声源进行计算，并通过多维交叉层法进行声源的识别定位，可得到该发动机在各工况下的声源立体分布。经多维交叉层法识别计算的结果增加了声源定位的准确性，并去除了声源投影带来的干扰，可对各种分布复杂的噪声源进行有效识别。

该技术仅需在各面进行一次台架变转速工况测试，即可对发动机各转速下、500～5 000 Hz频率范围内任意频率的声源进行识别定位，具有测试周期短、覆盖工况全面、识别精度高、结果直观、实用性高的优点，可广泛应用于各动力总成产品的噪声水平控制。

在波束形成识别结果的优化处理中，国内外学者通过反卷积理论建立波束形成输出、阵列点传播函数和声源真实分布之间的非齐次线性方程组，并通过迭代求解声源分布，该理论及其衍生求解方法可大幅降低传统波束形成直接输出结果的旁瓣影响。对于交叉层方法的识别结果，如结合反卷积方法进行优化，预计可达到更精细的识别效果，但由于交叉层法聚焦点数量较多，在反卷积处理过程中将生成大规模的点传播函数及方程组。对交叉层法结合反卷积的优化方法将在后续的研究中继续探索改进。