缝纫机针杆刺布机构的惯性力优化平衡研究*
2021-11-08徐建勇周永光
徐建勇,严 辉,周永光
(1.台州市产品质量安全检测研究院,浙江 台州 318000;2.台州方圆质检有限公司,浙江 台州 318000)
对于缝纫机而言,其运动机构主要是由四杆机构及其衍生机构连接而成的,在高速运转的过程中,机器中的曲柄滑块机构、RSSR 机构等会产生很大的周期性变化,由此产生惯性力和惯性力矩,进而造成机器的强烈振动和噪音,加剧机件的疲劳失效和磨损,降低机构的运动精度和平稳性,此外,也会影响到操作者的身心健康,因此,对其各连接机构进行平衡分析很有必要。而在平衡计算中,由于驱动力矩和阻抗力矩与机械工况有关,单独平衡惯性力偶矩往往没有意义,所以一般只对平面机构的总惯性力进行部分或完全平衡[1]。
针杆刺布机构几乎存在于所有的缝纫机中,且一般位于缝纫机机头处,相对于其他位置,其产生的不平衡惯性力和惯性力矩对整机的影响更大(例如平缝机等),因此要优先对其进行平衡分析。缝纫机针杆刺布机构是典型的曲柄滑块机构,但是对于常用曲柄滑块机构的部分平衡而言,其特殊性如下[2]:
(1)曲柄在恒速旋转时,只有连杆产生惯性力矩,而在惯性力部分平衡之后,惯性力矩的数值也比较小,此外,受制于空间限制难以做到完全平衡,因此,曲柄滑块机构的部分平衡主要是惯性力的部分平衡,通常采用附加平衡配重法。
(2)在计算平衡配重时,关键是最佳平衡量的求取。
(3)最佳平衡量的求取主要是平衡优化目标的选取。目前平衡目标的选取方法较多,在这里选取文献[2]中提出的综合考虑最大惯性力和惯性力绝对值的平均值两项优化指标部分平衡方法。
1 针杆刺布机构的运动分析
图1 中a 为缝纫机针杆刺布机构平面图,b 为对应的曲柄、连杆和滑块的运动简图。图中A 点为曲柄旋转中心,B 点为曲柄与连杆连接点,C 点为连杆与滑块连接点,滑块是在接近行程上下死点的区间内运动的,取行程的下死点C2为行程起点,滑块C2到C 点的滑块行程为S。图中其余参数:曲柄AB 长度为lAB,连杆BC 长度为lBC,过B 做直线BD 垂直AC 于D 点,曲柄逆时针旋转,转角为φ,AC 与BC 夹角为θ,当滑块处于如图所示位置,滑块的行程[3-4]:

图1 曲柄滑块机构运动及计算简图

上式即为滑块速度与曲柄转角关系,对其进行微分,即可求出滑块加速度:

式中:ω 为曲柄角速度,其他参数和前面的一致,由式(5)可知,当滑块的质量一定时,随着速度的增加,滑块所产生的惯性力也在快速增加。
2 针杆刺布机构部分平衡的理论计算
根据前面的分析,缝纫机针杆刺布机构的平衡主要是惯性力的部分平衡,运用的方法为平衡质量法也就是质量代换法,详细的计算如下[1,5-6]:
如图2 所示,对针杆刺布机构进行平衡时,先用质量代换法将连杆2 的质量m2集中于B、C 两点的质量m2B、m2C来代换,将曲柄1 的质量m1用集中于B、A 两点的质量m1B、m1A来代换。按照上面的质量代换,机构的惯性力只有两部分,即集中在B 点的质量mB=m2B+m1B所产生的离心惯性力FIB和集中于C 点的质量mC=m2C+m3所产生的往复惯性力FIC。

图2 曲柄滑块机构的平衡简图
为了平衡离心惯性力FIB,只需在曲柄反向延长线加一平衡质量m′使之满足

同理,利用静质量代换法求集中于C 点的移动质量为

为了平衡一阶惯性力,同样可以在曲柄的反向延长线上距A 为r 的地方再加一个平衡质量m″,并使

将平衡质量m″产生的离心惯性力FI″分解为一水平分力FIh″和一铅直分力FIv″,则有

式(15)中FIh″=FIC一阶惯性力,二者大小相等,方向相反,因此其与一阶往复惯性力平衡,但是又多出新的不平衡惯性力FIv″。如果多加的平衡质量m″=KmClAB/r,K≤1,则可抵消水平方向的部分一阶惯性力,而在铅直方向增加比一阶惯性力小些的惯性力,使机构达到部分平衡的目的,故总的所加平衡质量m 为

在已知的针杆刺布机构中,除平衡系数K 未知,其他参数全部已知,因此K 的取值大小直接决定可平衡梁的大小,从而决定平衡的效果,因此需要按照一定的优化目标选择K 的最优值。
3 针杆刺布机构部分平衡最佳平衡量的选取
已知剩余惯性力的大小

F1表示剩余惯性力的最大值,则F1=Fmax;
F2表示剩余惯性力绝对值的平均值,则F2=F,其求解只需对式(20)进行定积分运算即可。
在此优化平衡方法中,需要添加两个加权系数w1和w2从而把F1和F2同时考虑在内,得到的新的目标函数为

式中:w1+w2=1,且w1≥0,w2≥0,0≤K≤1。
由于F1代表的剩余惯性力最大值大于F2代表的剩余惯性力平均值,当F1的加权系数w1>0.2 时,就无法体现并考虑F2的效果,也就无法体现此平衡方法的优点。
为避免出现上述情况,一般取w1≤0.2,w2≥0.8,在文章的计算中,取w1=0.1,w2=0.9。
式(20)中K 为平衡系数,也是目标函数的设计变量之一。对于一个确定的曲柄滑块机构,式(20)中除K值以外,其他所有的数值均是已知量,因此要想求出目标函数F(K)的最优值,最主要的就是求出使目标函数为最小值的K 值。
已知0≤K≤1,显然上面的计算比较复杂,需借助Matlab 软件进行求解,结合缝纫机的三维模型,各部件的参数如表1 所示。

表1
已知缝纫机的主轴转速为6000r/min,将表2 的各数据代入到相应的函数中,剩余惯性力F 可表示为

表2

将式(22)输入到Matlab 中进行计算,由于上式中有两个变量,现对K 在区间(0,1)间每隔0.1 取值一次,如图3 所示。
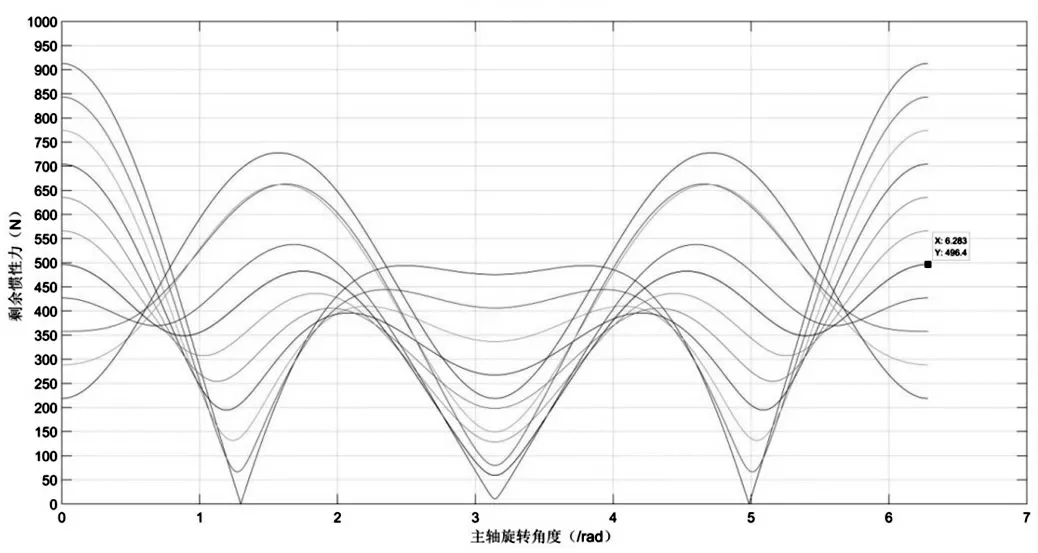
图3 不同K 值对应的剩余惯性力
由图3 可知,当K=0.6 时,剩余惯性力的最大值F1取得最小值,但是其精度不够高,需要在附近搜索最优值,经过在Matlab 中进一步的计算可知,当K=0.593 时,目标函数F(K)min=0.1F1+0.9F2=380.5037,如图4 所示。

图4 最优配重和未做配重时的剩余惯性力
图4 中,剩余惯性力幅值、平均值及目标函数分别由912.8、461.685、506.797 降低到501.2、461.685、380.504,降低幅度达45%、20.5%、24%,减少的效果非常明显。
现计算外加平衡质量,当K=0.593 时,针杆刺布机构总的所加平衡质量m 为

由上式可知,其他条件不变时,mr 的乘积为一恒定值,总平衡质量m 的大小与质心r 成反比,但是考虑实际零部件的密度及可安装的空间,二者的大小又处于一个可选范围内,针杆曲柄的配重加在了原有轴线的反向延长线上,因此配重部分的重心r 在12.5 附近。
经过计算,配重块外圆半径R=25.982mm,其对应的质心r=12.6886mm,m=133.9145g,mr=1699.18,与理论数值1698.99 近似相等,而原有的配重块外圆半径为23mm,这主要是因为当曲柄的长度由原有的15.5mm 增加到现在的16.7mm 之后,曲柄滑块机构间的不平衡惯性力也相应地发生了改变,因此对应的配重块的质量也需要随之做出改变,结合实际的三维模型并经过详细计算可知,相对于原有的配重块,新的配重块质量增加了35.36g,其外圆半径也由原有的23mm增加到25.982mm。
4 针杆刺布机构优化对整机振动的影响分析
针杆刺布机构作为整机多个机构中的一个,单独对其进行分析是远远不够的,为了更准确地分析其对整机振动的影响,并验证理论计算的准确性,很有必要将其放入到整机中进行计算。现结合Adams 多体动力学软件对平衡前后的针杆刺布机构整机振动的影响进行分析。将缝纫机整机模型导入并进行相应计算。
为了更好地反映出针杆刺布机构的平衡配重对整机振动的影响,分别在上节机壳头部和尾部以及下节的针板共三处建立振动测量点,运用Adams 计算出三个位置在机器运动过程中各方向的加速度变化。已知给定的机器运转速度为6000r/min,其中X、Y、Z 分别代表缝纫机的轴向、竖直方向、前后方向,平衡块修改前后三个测点在X、Y、Z 三个方向的加速度如图5 所示。

图5
由图5 可知,改为新的平衡块之后,针板处X、Y、Z三个方向的振动加速度均降低了,其中Y 和Z 方向的下降幅度较大。
由图6 可知,改为新的平衡块之后,上节机壳头部X、Y 两个方向的振动加速度均降低了,且降低的幅度较大,但与此同时Z 方向即机器的前后方向振动加速度增加了,且增加的量较多。
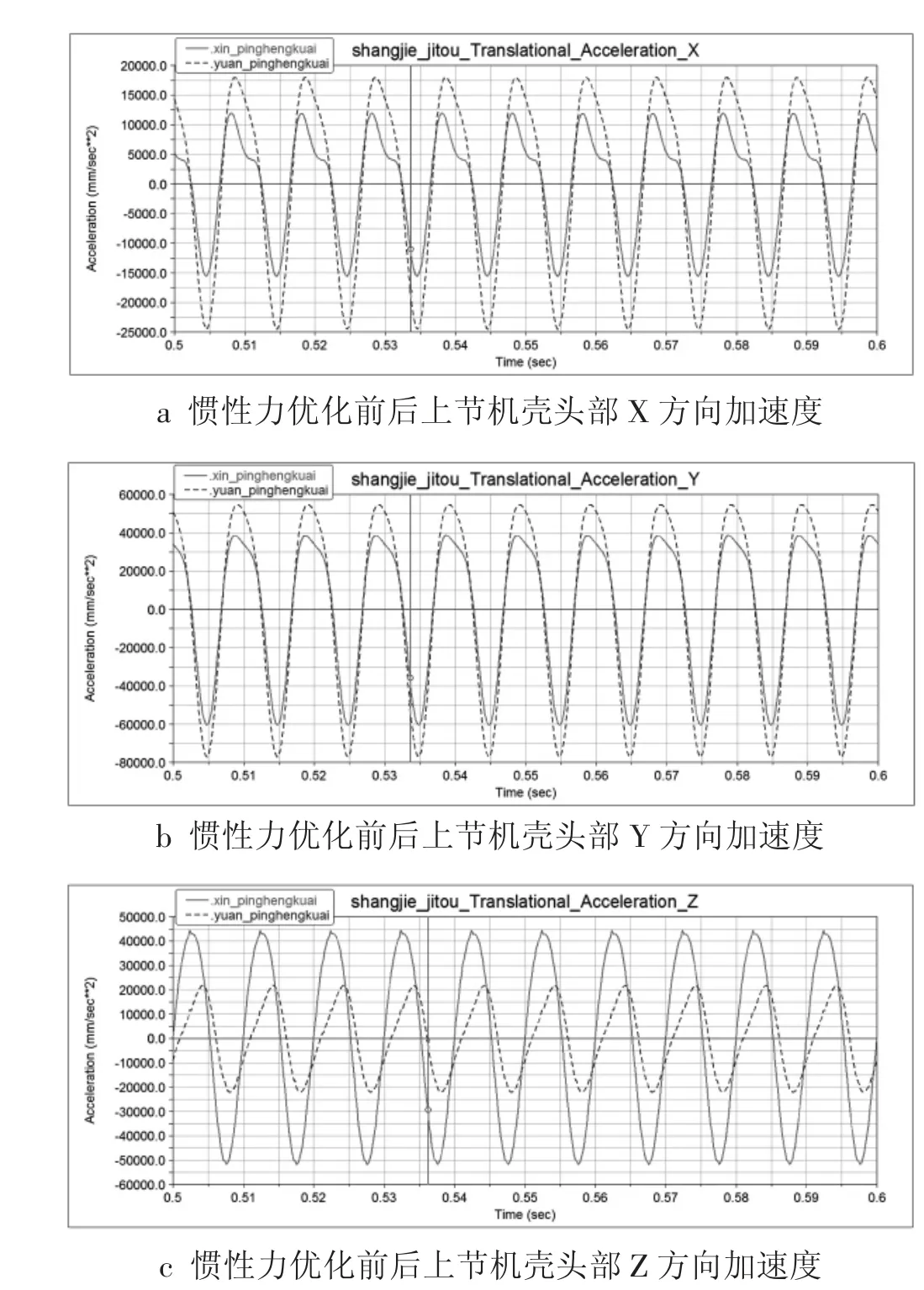
图6
由图7 可知,改为新的平衡块之后,上节机壳尾部X、Y、Z 三个方向振动加速度的变化趋势与上节机头处一致,即X、Y 两个方向的振动加速度均降低了,Z 方向振动加速度增加,但是两处增加和减小的幅度不同,三处加速度变化的详细数值如表3 所示。

图7
结合表3 的数据可以看出,针杆曲柄的配重在优化之后,整机除去上节机壳在Z 方向(前后方向)的振动加速度是增加的,其他各方向的振动加速度都是降低的,特别是在针板处Y、Z 方向的振动加速度降低幅度达到30%左右,这有利于提高缝制过程的稳定性;而上节机壳无论头部还是尾部,配重优化之后上节机壳在Z 方向的振动加速度都增加了,且增加的百分比较大,而且越靠近头部增加的幅度越多,但是增加的量相对都不大;与此同时,头部和尾部在X 和Y 方向的振动加速度都大大降低了;综合来看,针杆曲柄配重优化之后整机的振动情况有了较大改善。
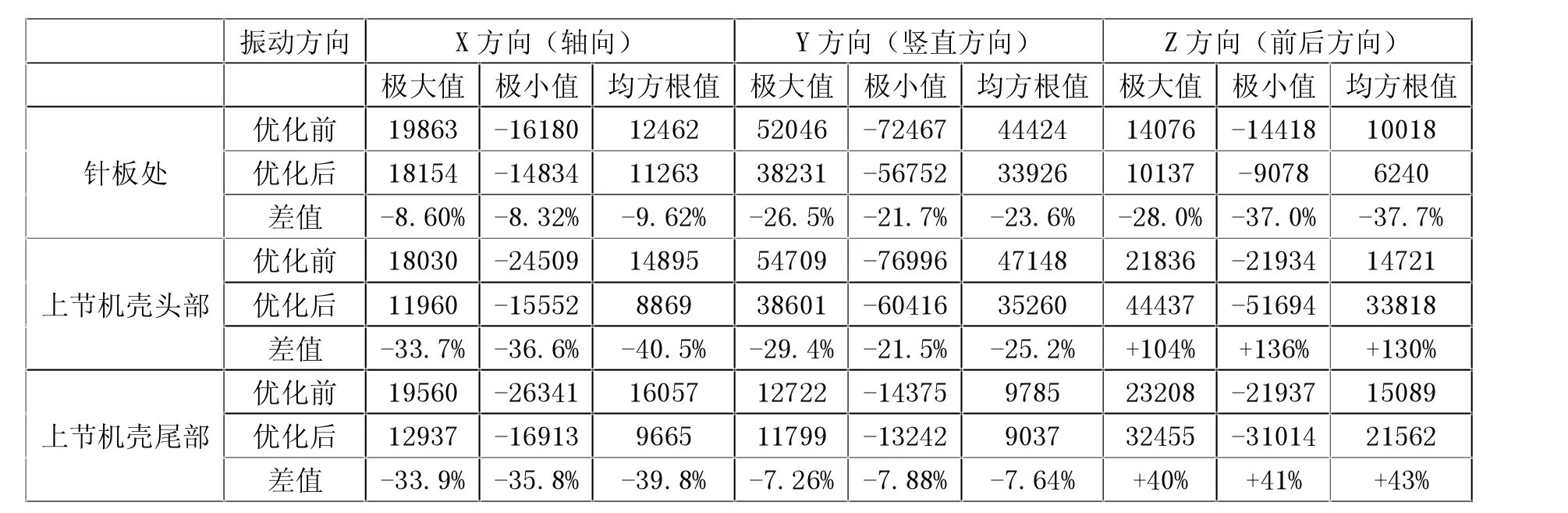
表3 惯性力优化前后各测点的振动加速度对比(单位:mm/s2)
5 结论
文章以缝纫机针杆刺布机构为例,对曲柄滑块机构惯性力产生的机理做了详细分析,利用平衡配重法对部分惯性力的平衡进行了理论计算。理论计算表明,针杆曲柄的杆长和质量的变化都会影响到最终配重的大小,Adams 仿真计算也表明,针杆曲柄优化之后整机的振动会有较大幅度的降低,这也证明了理论计算的正确性。
