基于SWIPT中继系统的信道容量性能分析
2021-11-08刘洁梅刘开旭
刘洁梅,林 霏,王 叶,刘开旭
齐鲁工业大学(山东省科学院) 电子信息工程学院,济南 250353
随着科技水平的提升,世界已经进入5G时代,5G通过引进增强型移动宽带 (eMBB)、高可靠与低时延 (uRLLC)和增强型机器类连接(eMTC)等新型技术,将垂直行业应用设备等纳入了通信的范畴[1]。系统在接受更多信息的同时也在加剧着对能源的消耗和需求。随着传输距离的增加,过长的传输路径和不确定的信道衰落情况也给信息传输带来了不小的影响。经研究发现,无线射频(Radio Frequency ,RF)信号既可以传输信息,也可以携带能量,同时,中继的存在改善了远距离传输带来的信道衰落,扩大了通信范围。因此,无线携能通信技术(Simultaneous Wireless Information and Power Transfer ,SWIPT)和中继系统的结合在诞生之初就受到人们的广泛关注。
无线通信不断增长的需求使得研究容量性能变得越来越重要,它是衡量传输系统优劣的重要指标之一。研究表明,SWIPT技术可以降低中继节点的能量消耗,但没有从通信的可靠性和有效性入手对系统进行性能分析[2-3]。郑阳等[4]从通信的可靠性入手,将具有能量收集中继的协作认知无线电(Cognitive Radio,CR)网络与传统CR网络做对比,分别研究在发射功率有限和无限情况下的中断概率。殷思兴[5]和李胜贤[6]等从通信的有效性入手,分别研究了具有时隙模式的能量收集CR系统的吞吐量和当次用户同时进行能量收集和复用主网络频谱时,次用户的吞吐量最大化问题,较全面的分析了SWIPT中继系统的遍历容量性能,但并没有考虑信道衰落和信道状态信息(CSI)对信道容量的影响。
本文针对一种SWIPT与中继传输结合的SWIPT协作通信系统,研究了其不同类型的信道容量。在仅接收端知道CSI的情况下,给出了该系统的遍历容量和带中断概率的信道容量的理论分析。然后在收发两端均知道CSI的情况下,使用不同的功率分配法如注水功控法、信道反转法、截断式信道反转法对功率进行分配,得到对应的信道容量的理论分析。最后给出了仿真结果,得出结论。
1 SWIPT中继系统模型
本文的系统模型如图1所示。图中S 代表系统中的主用户,即系统发送信号的源端;R代表中继节点,用来接收源端发送的信息,转发获得的信息,并从中获取能量供自身使用;D代表目的端,即信号最终到达的目的地。
周迅等[7]提出了两种可实现的接收机架构,分别是功率分割模式(Power Splitting,PS)和时隙切换(Time Switching,TS)模式。PS模式将接收到的信号按照功率分割因子分为能量收集部分和信息解码部分。TS模式将接收到的信号按照时隙进行划分。一部分时隙内的信号进行能量收集,另一部分时隙内信号进行信息解码。本文采用的是PS模式,设置功率分割因子为α。信号由源端发出,同时在两条路径上传输,可沿直连路径传输至目的端,也可先到达中继节点,经由中继接收后采用放大转发的形式将信号发送至目的端,中继处将接收到信号分为两部分,一部分经过信息解码处理继续传输至目的端。另一部分通过能量收集、获取自身可用的功率,帮助主用户传递更多的信息。最后在目的端利用最大比合并将两信道信息进行合并获得最终接收到的信号。
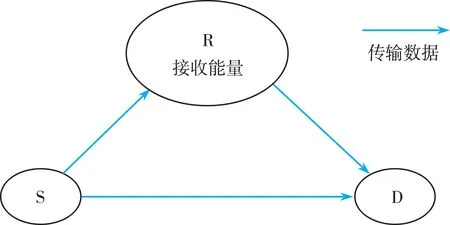
图1 SWIPT双信道系统
2 容量分析
2.1 系统瞬时接收的信噪比分析
SWIPT中继系统分别有源端到目的端的直连路径和源端到中继再到目的端的中继路径。
其中Ps是主用户的发送功率,nsd和nr分别是主用户(源端)到目的端信道和中继R处的加性高斯白噪声。噪声具有零均值和方差n0sd和n0r,hsd和hsr分别为源端到目的端和源端到中继的信道衰落系数。直连路径的瞬时接收信噪比为[8]:
(1)
其概率密度函数为[8]:
(2)
中继路径的瞬时接收信噪比为[8]:
(3)
其概率密度函数为[8]:
(4)
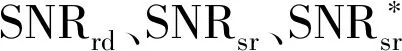
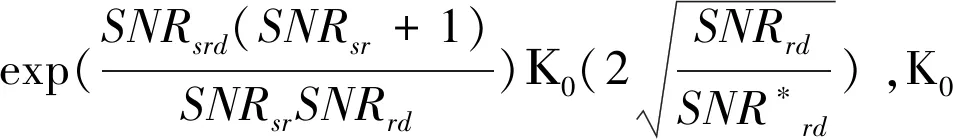
此时SWIPT中继系统接收端总信噪比为:
SNR=SNRsd+SNRsrd。
(5)
2.2 接收端已知CSI分析
本文进一步考虑信道衰落,研究遍历容量和带中断概率的信道容量。
2.2.1 遍历容量
接收端已知CSI的遍历容量定义为最大化数据传输速率且其误码率足够小,也将其称之为香农容量。此时仅有接收端已知CSI,因此发送端不能调整发送功率以适应于信道。本文的SWIPT中继系统中,两条路径作为一个整体求解遍历容量,其中带有无线携能技术的中继在收集射频信号能量的同时不传输自身的信息,只协助传输主用户信息。
本文所有信道容量公式均为归一化的信道容量公式,在目的端已知信道状态信息时的遍历容量公式可表达为[8]:
Cbianli=E[log2(1+SNRsd+SNRsrd)],
(6)
式(6)的闭合表达式需要根据直连路径和中继路径信噪比的概率密度函数取数学期望给出,非常复杂,因此,利用Jensen不等式[9]可得一个简化的上界为:
Cbianli=Ε[log2(1+SNRsd+SNRsrd)]
≤log2(1+Ε[SNRsd]+Ε[SNRsrd])
=log2(1+SNR*sd+SNR*srd)。
(7)
2.2.2 带中断概率的信道容量
带中断概率的信道容量在接收端已知CSI的前提下,定义为信道在固定的中断概率之下以最大的传输速率恒定的传输数据。处于中断的信道衰落较强,无法满足正常传输数据的要求。带中断概率的信道容量在处于中断状态的信道里不传输数据,重点依靠信道条件好的信道,从而提升发送信息的固定速率。
与单一无SWIPT直连路径的带中断概率的信道容量不同,本文的SWIPT中继系统要求直连路径和中继路径总信噪比与预设的门限值SNRmin比较,大于或等于门限值才能正确译码,在带宽为1的情况下按照log2(1+SNRmin)的最大速率进行传输,由于SWIPT中继收集的能量作为放大转发中继接收信号的功率,系统的总信噪比大幅提高,相比于单一直传路径所获中断容量也更高。若总信噪比小于SNRmin,发生中断,中断概率为Pout,此时直传路径和中继路径停止传输信息,整个系统总信噪比归为零。SWIPT中继系统可正确接收的带中断概率的信道容量公式如下:
Cout=(1-Pout)Ε[log2(1+SNRmin)],
(8)
2.3 收发两端都已知CSI分析
本文在SWIPT中继系统中进一步考虑信道衰落和信道状态信息,研究带各类功率分配法下的收发两端都已知CSI容量。
2.3.1 注水功控法分配功率下的香农容量
在收发两端都知道CSI的情况下,发送端通过允许瞬时发送功率随着信噪比变化来进行功率控制,不存在中断信道和带中断概率的信道容量,这里的香农容量与只有接收端已知CSI时的遍历容量相对应,但不同的是,此种状态下存在功率控制和中断门限SNR0。
发送功率沿时间进行最佳分配,即注水功控法,如图2所示,但瞬时的发送功率根据功率限制条件存在中断门限SNR0,本文接收端总信噪比反映了直连路径和中继路径两个信道状态条件,其中中继本身存在各种可能状态,总体信道情况也随中继协助状态和信道衰落有好有坏,总体信道条件达不到SNR0要求时不进行数据传输,达到SNR0要求时正常使用信道。

图2 最佳分配功率:注水功控法
由图2可知,在系统正常使用信道时,根据SWIPT中继系统信道的不同瞬时信噪比分配不同的功率,总信噪比大信道条件好时,分配功率和传输速率高,总信噪比小信道条件差时,分配功率和传输速率低,图中用双箭头符号标注出的为实际分配功率,相较于单一直传无SWIPT中继路径,本文的两条路径传输信号更多,瞬时信噪比更大信道条件更好,根据注水功控法分配的功率也更大,因此香农容量较单一直传无SWIPT路径提升。收发两端都已知CSI情况下的香农容量公式如下:
(9)
2.3.2 信道反转法分配功率下的零中断容量
由于存在其他不确定因素,学者又提出了两种次佳的功率分配方法,它们所获容量小于注水功控法分配功率下的香农容量,但实现方法简单。信道反转法就是其中之一。信道反转根据发送端已知的CSI来保持接收端的稳定接收功率,不存在中断门限,公式如下:
(10)
系统中此方法不考虑直传路径和中继路径的状态,固定以某一速率传输数据,传输过程不会发生中断,又被称为零中断容量。本文瑞利衰落下,此容量持续为零,因为此时E[1/SNR]无穷大。
2.3.3 截断式信道反转法分配功率下的下的最大中断容量
SWIPT中继系统可在深衰落信道状况时停止传输数据,提高其他信道下的传输速率,此容量称为中断容量,此方法为另一种次佳的功率分配法截断式信道反转法。此情况存在中断门限。当总信噪比小于中断门限时,不传输数据,当总信噪比大于中断门限时,分配固定功率,通过优化中断门限,得到对应的最大中断容量,公式如下:
p(SNR≥SNR0),
(11)
3 仿真性能
本文基于SWIPT中继系统,对不同容量进行研究对比,信道处于瑞利衰落下,使用QPSK对信号进行调制解调,中继以放大转发的方式传递信息,目的端以最大比合并接收信息。不特殊声明的情况下,源端到中继,源端到目的端和中继到目的端的信道方差均设为1。
3.1 接收端已知CSI分析
3.1.1 遍历容量与带中断概率的信道容量对比
将不同中断概率的容量与遍历容量对比,仿真曲线如图3所示。

图3 遍历容量与带中断概率的信道容量对比
由图3可知,在SWIPT系统中,不同的中断概率影响着系统容量。
3.1.2 门限对带中断概率的信道容量影响
预设不同的门限值,通过蒙特卡罗法确定对应的出现中断的概率,来观察门限对带中断概率的信道容量的影响。仿真结果如图4所示。

图4 门限对带中断概率的信道容量影响
由图4可知,随着门限值SNRmin的提升,带中断概率的信道容量逐渐下降,最后归零。因为当门限值较小时,总信噪比大于门限的情况多,大于门限的总信噪比会进行正确译码,因此带中断概率的信道容量值较高。随着门限的增高,对信道要求也就高了,可以正确接收的信号也减少了。当门限达到一定数值时,信道的总信噪比小于门限,发生中断,信道不再传输,容量为零。因此可通过优化门限值来优化带中断概率的信道容量。
3.2 收发两端都已知CSI分析
3.2.1 门限对最大中断容量影响
以最大中断容量为例,研究门限大小对收发两端都已知CSI情况下最大中断容量的影响。仿真结果如图5所示。

图5 门限对最大中断容量影响
图5中横坐标r0表示中断门限,前期门限值不高的情况下对中断容量的影响较小。中断容量只在信道的总信噪比大于等于中断门限时使用信道,门限值不高意味着信道信噪比多高于中断门限,此时的中断容量存在最大值,当中断门限达到一定节点时,会有中断状态发生,即停止发送数据,最大中断容量也会随之下降。
本文同时预设了不同的源端到目的端,源端到中继和中继到目的端的信道方差,信道方差越大,两个端点间距离越近,信道状况越好,衰落越小,信道的总信噪比相对越大,对应的最大中断容量越大。图5仿真结果验证了理论。
3.2.2 各容量仿真结果对比分析
对遍历容量,注水功控法分配功率下的香农容量,信道反转法分配功率下的零中断容量和截断式信道反转法分配功率下的最大中断容量通过蒙特卡罗法进行仿真对比和性能分析。仿真结果如图6所示。

图6 各容量仿真结果对比分析
本系统的中继可以收集能量,注水功控法和截断式信道反转法又分别对发送功率进行了最优、次优分配。由图6可知,与无SWIPT技术单信道相比[9],收发两端已知CSI的香农容量高于仅接收端已知CSI的遍历容量;最大中断容量在低信噪比时略小于遍历容量,但随着信噪比增加,二者趋于一致;零中断容量在瑞利衰落下为零。由此可见SWIPT中继系统帮助传输容量,且在有功率分配法分配功率的情况下提升明显。
4 总结与展望
本文通过提出SWIPT中继系统的模型,在仿真中预设不同的中断门限值来观察门限对系统容量的影响,利用蒙特卡罗法对不同情况下的容量进行了性能对比。仿真结果证明,具有SWIPT技术的中继系统容量优于传统的无SWIPT单信道系统容量,尤其在信道考虑功率分配法时,系统容量提升明显,具有一些应用意义。可在设备网络中增加具有能量收集技术的应用设备,并对相关功率进行分配,既能从接收信号中获取能量提高能源利用率又能提升系统整体传输容量,做到缓解能源紧缺,减少成本,增加用户体验感。
